基于改进Prim 算法的路径规划研究

李耀东，苗春艳，高 健，刘辛垚

（1.呼伦贝尔市气象局，内蒙古 呼伦贝尔 021008；2.呼伦贝尔市阿荣旗气象局，内蒙古 呼伦贝尔 162700；3.乌兰浩特市气象局，内蒙古 乌兰浩特 137400）

0 引言

路径规划问题可以被形式化为在一个离散或连续的状态空间中找到一条从起点到终点的最优路径。路径规划在很多领域都具有广泛的应用，如：在高新科技领域包括无人机的避障飞行、导弹躲避雷达搜索、突防爆破等；在日常生活领域包括GPS 导航、道路规划等；在决策领域包括物流管理中的车辆问题（VRP)等；通信技术领域的路由问题；等等。凡是可拓扑为点线网络的规划问题基本上都可以采用路径规划的方法来解决[1]。

路径规划的核心就是算法的设计，路径规划算法目前已经得到了广泛的关注，算法更加智能[2]。根据对环境信息的把握程度，可把路径规划划分为基于先验完全信息的全局路径规划和基于传感器信息的局部路径规划两种类型[3⁃5]。最小生成树（MST）作为图论中最经典的算法之一，由于具有诸多优势，在规划、网络和医学等各个领域的路径规划中得到了广泛的应用[6]。在最小生成树算法中，Prim 算法给出了一个寻找最小生成树的算法，适用于稠密图，并能够将求解的时间复杂度最小化[7]。

本文主要研究Prim 算法的路径规划，属于静态路径规划范畴。

1 算法概述

图论中将连通所有站点的无向图称为生成树，最小生成树是一幅有加权但是无方向的最小连通子图。

在一个给定的无向图G=（V,E）中，（u,v）∈E，代表连接顶点u和v的边，w（u,v）代表此边的权重，若T⊆E，即存在T为E的子集，且（V,T）为树，使得w（T）=Σ（u,v）最小，则此T为G的最小生成树。

Prim 算法由美国计算机科学家罗伯特·普林（Robert Prim）在1957 年提出，它是求解无向带权图的最小生成树的经典算法，可以应用于网络设计、城市规划、交通规划等领域。该算法最初是为了解决通信网络中的连通性问题而设计的，后来被广泛应用于图论领域，特别是最小生成树问题。

Prim 算法是一种贪婪算法，用于查找加权无向图的最小生成树。其主要思想是以点选边，适用于稠密图。Prim 算法首先从任意顶点开始，然后向树中添加权重值最小的边，这个最小的边的另一端顶点尚未在树中，若已在树中则将该边舍去，从余下的边中再选最小的边进行添加，直到所有顶点都在树中。Prim 算法的关键是在每一步做出局部最优选择，从而找到全局最优解，这种贪婪的策略保证了最终树是最小生成树[8⁃9]。

如图1 所示，5 个顶点A、B、C、D和E之间的边带有权重，用数字表示，各顶点间的权重如表1 所示。

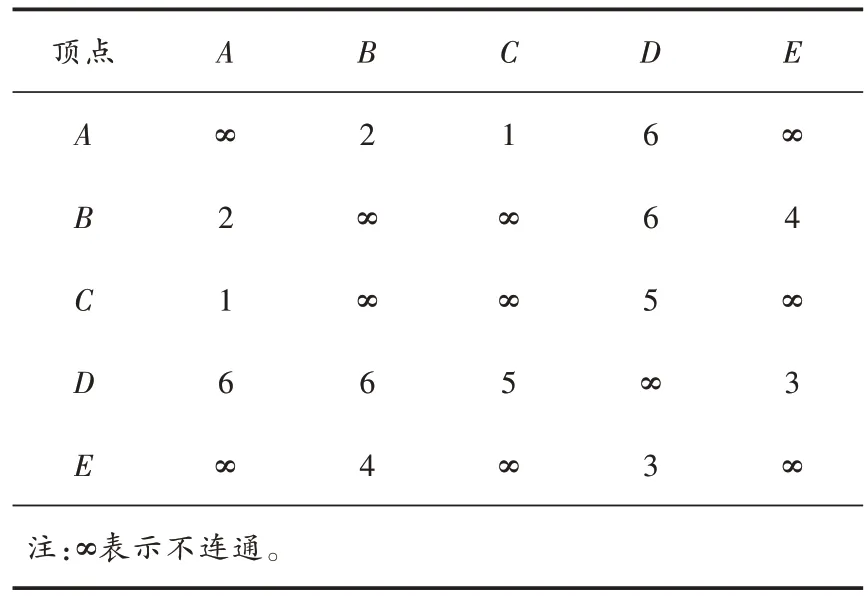
表1 各顶点间权重计算表

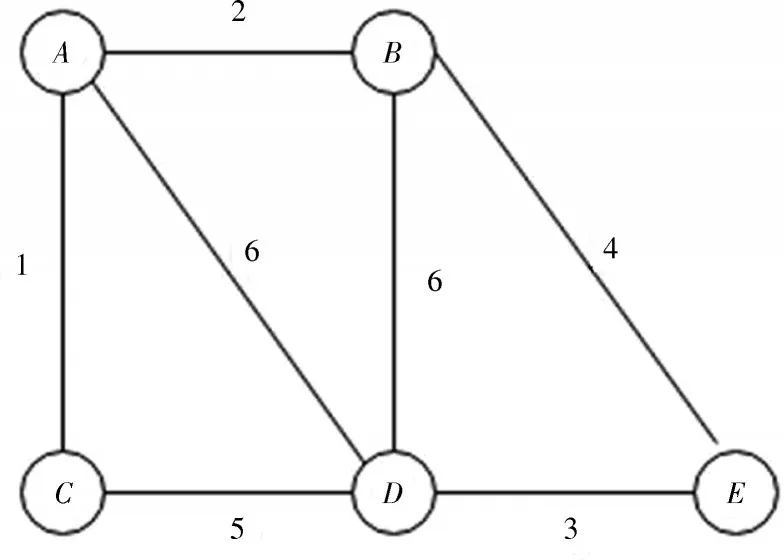
图1 Prim 算法示例图

由表1 可知，采用Prim 算法计算的最小生成树是连接所有顶点的最小成本路径，这个路径的总成本是1+2+5+3=11。原始Prim 算法时间复杂度为O（V2），其中V是节点的数量，因为在每一步中需要遍历所有与最小生成树相邻的节点以找到距离最短的节点。

除了Prim 算法，还有其他求解最小生成树问题的算法，比如Kruskal 算法[10]等，但这些算法各有优缺点。

2 改进的Prim 算法

2.1 算法的改进

在实际应用中，Prim 算法存在一些缺点，例如对于大规模稠密图，其时间复杂度较高，且在图的结构发生变化时，需要重新计算整个最小生成树。为了解决这些问题，学者们提出了一系列改进Prim 算法的方法：一种改进是使用堆来维护所有与最小生成树相邻的节点，以便快速找到距离最短的节点；另一种改进是使用斐波那契堆来维护所有与最小生成树相邻的节点[11⁃13]，其中最为重要的是基于聚类分析的改进。聚类分析是一种无监督学习算法，主要用于处理无标签数据。聚类分析的目的是通过将相似的数据点分为一组来形成聚类，从而有助于了解数据的内在结构，识别异常数据，找到数据中的模式等。虽然Prim 算法和聚类分析在处理数据类型和目的上有所不同，但它们都是数据分析领域中非常重要的算法。在实际应用中，可以将它们结合起来使用，比如通过聚类分析对数据进行分类后，再使用Prim算法构建聚类中心之间的最小生成树，以便更好地了解数据之间的关系和结构[14]。本文探讨如何将这两种算法结合起来，计算聚类分析中的最小生成树。

下面是使用聚类分析改进的Prim 算法最小生成树的基本步骤：

1）将所有节点分成若干个聚类；

2）选取一个聚类中心点作为起始点；

3）找到与该点最相似的另一个聚类中心点，将其作为下一个点；

4）对于其他尚未加入最小生成树的聚类中心点，计算它们与最小生成树上所有点之间的相似度，并选择其中最小的那个点作为下一个点；

5）将新加入的点与最小生成树上已有的点连接起来，形成一条边，并将其加入最小生成树；

6）重复步骤4）、步骤5），直到所有聚类中心点都被加入到最小生成树中为止。

通过构建聚类中心之间的Prim 最小生成树，对稠密图路径规划复杂性进行分解，还可以以多个聚类中心为基点，再聚类构建更小范围的Prim 最小生成树，有助于进行路径规划数据的分析和决策。

2.2 改进算法的局部最优

使用改进的Prim 算法计算无向图的最小生成树，将最小生成树划分成若干个簇，其中每个簇对应于一条或多条连接相似节点的路径。下面用一个简单的例子来说明聚类分析改进的Prim 算法的实现过程，如图2所示。

图2 聚类中心最小生成树

如图2 所示，构建一个包含6 个节点的最小生成树。首先，将每个节点看作一个聚类，并计算节点之间的距离；然后，按照距离度量的大小，将最小的两个聚类合并成一个新的聚类；接着，继续按照距离度量的大小，将最小的两个聚类合并成一个新的聚类；最终，得到整个图的最小生成树。有6 个聚类中心，分别是：C1、C2、C3、C4、C5和C6，这些聚类中心之间连接了一些边，这些边的权重是一个正整数。这些边被用于构建最小生成树，是连接所有聚类中心的最小成本路径。在最小生成树问题中，聚类分析可以用来快速判断两个节点之间是否连通，并将节点分成若干个聚类，从而减少Prim 算法的计算量。通过聚类分析的改进，Prim 算法的时间复杂度得到了大大优化，尤其是在处理大规模稠密图时，其效果更加明显。此外，基于聚类分析的改进Prim 算法还具有较强的鲁棒性，能够适应图的结构变化。

3 路径规划实践

3.1 原路径规划

目前，呼伦贝尔市各类自动气象站遍布全市各个乡镇，如图3 所示。利用欧几里德距离公式，以站网中各站点经纬度计算各站间距，以各站间距为站点间边界的权重计算原Prim 最小生成树，如图4 所示。

图3 呼伦贝尔市气象站点分布图

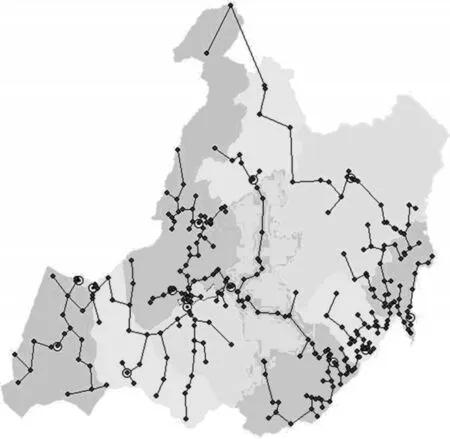
图4 原Prim 最小生成树分布图

由图3、图4 可知，经过在地理信息系统Arcgis 上计算，原Prim 最小生成树连通的全部站点的连通路径长度为5 178 km。呼伦贝尔市气象站网中站点分布零散，仅在县（区）域政府周边站点路径集中，图上有明显的连通中心，位于呼伦贝尔市中部。原Prim 最小生成树虽对站点路径连通情况做了初步规划，但对站网中站点分布状态并没有量化的判别，站点分布状态判别只是以定性判别为主。

3.2 路径再规划

3.2.1 K⁃Means 聚类分析

利用K⁃Means 算法将呼伦贝尔市气象站网进行聚类划分，计算站点与类簇质心的距离，与类簇质心相近的站点划分为同一类簇。通过站点间的距离来衡量它们之间的相似度，两个站点距离越远，则相似度越低；否则，相似度越高。由图3、图4 可知，呼伦贝尔市气象站网中站点分布既有密较集的中心区，又有孤立的站点，通过聚类分析可以很好地将站点密集区与孤立站点定量化表示出来。为达到上述目的，在K⁃Means 聚类分析中以二分法不断递减选择站点聚类中心（n为站点个数，X为指数，偶数时聚类中心个数为n×2-X，奇数时聚类中心个数为n×2-X+1），因站网中站点个数为313 个，所以本次在二分法中X=1，即选择聚类中心个数为313×2-1+1=157 个，经过计算生成表2。

表2 站点个数＞1 的聚类中心统计表

由表2 可知：

1）站点个数＞1 的聚类中心共有74 个，聚类中心平均站点个数约为3 个，中位数为3 个，众数为2 个，聚类中心站点个数最多的为9 个，站点合计数为230 个，占总站点的73.5%。

2）站点距各聚类中心平均距离5.87 km，站点距各聚类中心4～6 km距离最多，最大11.76 km，最小为2.08 km。

3）站点个数为1 个的聚类中心，其分布孤立，离其他聚类中心较远，如图5 所示，可见，此次聚类可以很好地对原站点空间分布特征进行定量表述。

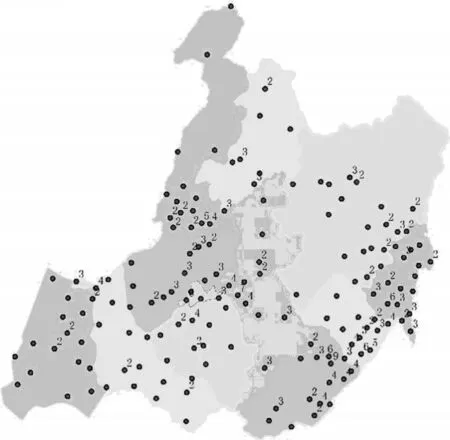
图5 二分法聚类中心分布图

3.2.2 聚类中心间路径规划

如图6 所示，改进的Prim 最小生成树连通全部聚类中心，呼伦贝尔市各县域中心在站网路径规划中连通作用明显，是站网路径连通的关键点，呼伦贝尔市海拉尔区是整个站网连通的中心。

图6 改进的Prim 最小生成树分布图

经过计算，改进的最小生成树的连通路径长度为4 620 km，路径长度缩短10.8%，各聚类中心中站点至各中心平均距离为5.87 km，改进后的Prim 最小生成树达到优化路径的目的。

改进的Prim 算法的基本思想与标准Prim 算法相同，但是它在选择下一个顶点时使用了一种更加高效的方法。标准Prim 算法通过检查所有的边来选择下一个顶点，这个过程的时间复杂度是O（n2）。其中，n是无向连通图顶点个数。改进的Prim 算法是将稠密图转向稀疏图，将Prim 算法的时间复杂度无限接近于Kruskal（克鲁斯卡尔）算法，时间复杂度为O（ElogV）。其中，E是边数，V是顶点数。改进的算法减小了E和V，降低了空间复杂度。

4 结论

本文提出的基于聚类分析改进Prim 最小生成树的路径规划算法适用于稠密图。首先采用二分法将气象站网中的站点先聚类，形成微小的站点聚类中心，再以各聚类中心进行Prim 最小生成树路径规划，从而达到路径规划的目的。

原站网布局中站点的分布杂乱零散，分布特征多定性描述，难以定量化分析；而改进的Prim 最小生成树算法仍遵循局部最优达到全局最优原则，先简化了站网中因站点分布不均匀而产生的复杂度，通过聚类分析的聚类中心，以二分法指数递减聚合站点，形成新的站网布局。

在呼伦贝尔市新的聚类站网布局中，站点个数大于1 个聚类中心占总聚类中心的47%，站点总数占站网的73.5%，聚类中心中站点距各聚类中心平均距离为5.87 km，最小生成树路径长度缩短10.8%。可见，改进后的算法定量化了站点空间分布特征，通过聚类增强了最优解，从而达到减小路径长度的目的。

需要注意的是：改进Prim 算法需要根据具体应用场景和问题规模来选择合适的指数，对于更加稠密的站网，指数选择应大于1，这样才可以更好地简化站网布局，将Prim 算法的时间复杂度无限接近于Kruskal 算法，降低算法的空间复杂度，以达到更好的实际应用目的。