鲁北平原雨量站网分布与面雨量误差关系研究

刘祖辉 刘海宇

（1.山东省水文中心 济南 250002 2.枣庄市水文中心 枣庄 277800）

面雨量为气象与水文结合的纽带，是江河流域防汛抗洪调度中一个非常重要的参数，河道的流量及水库的蓄洪规模均与其密切相关，因此客观、准确地计算面雨量对防汛抗洪及防灾减灾意义重大。近年来，国内外开展了大量面雨量计算方法的对比分析研究，部分成果已得到广泛的业务应用。本文以鲁北平原为研究区域，利用抽站法原理，采用1956—2016年降水资料，分析雨量站点密度、分布均匀度对面雨量误差的影响，以期为水文站网规划、改进降水插值方法、研究洪水预报模型输入误差等提供科学依据。

1 研究区概况及面雨量计算方法

1.1 研究区概况

鲁北平原地处山东省北部地区，位于东经115°16′～119°06′、北纬35°47′～38°10′之间，南以金堤河、黄河为界，北隔卫运河、漳卫新河与河北省相邻，西接河南省，东临渤海。流域覆盖聊城、德州两市和滨州、东营两市黄河以北地区，总面积30942km2。本区域为黄河冲积平原，区内主要有徒骇河、马颊河、德惠新河等河流，呈西南—东北向纵贯全区。

1.2 面雨量计算方法

面雨量估算方法主要有泰森多边形法、算术平均法、等雨量线法和网格法等。本文采用泰森多边形法。

泰森多边形法又称垂直平分法或加权平均法，该法首先计算出雨量站面积权重系数，将站点雨量与其所占面积权重相乘后累加即得到面雨量。雨量站权重系数求法：将流域内各相邻雨量站用直线相连，作各连线的垂直平分线，平分线相交将流域划分为若干个多边形，每个多边形内均有且仅有一个雨量站，设雨量站所在的多边形控制面积为 ΔA，ΔA与全流域面积A之比即为该雨量站的权重系数，面雨量计算公式为：

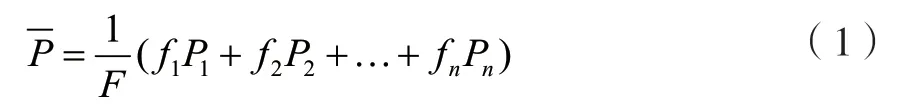
式中：f1，f2，…，fn分别为各雨量站泰森多边形的面积，F 为流域总面积；P1，P2，…，Pn，分别为各雨量站同时期降雨量和流域面雨量。

2 计算过程及关系分析

2.1 确定站网分布

在站网规划中，常利用抽站法研究站网布设合理性。一般将站网稠密地区的全部降雨资料计算的面雨量作为面雨量近似真值，然后按照分布均匀的抽站原则抽去一部分雨量站，再计算面雨量及其误差，寻求误差与布站密度的关系。为研究面雨量计算结果与站点分布的关系，借鉴抽站法原理，利用鲁北平原65 个雨量站点1956—2016年资料计算的面雨量作为面雨量近似真值，然后利用随机抽样的原理，按照55、45、35、25、15 站的数量抽取雨量站点，组成5 种站网分布，对每种站网分布确定泰森多边形权重，计算面雨量，然后将不同站网分布下的面雨量作为理论值，统计近似真值与理论值之间的误差，研究误差与站网分布的关系。

2.2 均匀度计算

雨量站网分布合理性评价可包括几个方面：站网密度、站网分布均匀性、站点高程分布等。为研究面雨量误差与站网分布均匀性的关系，引入站网分布均匀度指标描述站点分布情况。在鲁北平原区内，对确定的站网分布，利用泰森多边形法计算每站的控制面积，用下式计算站网分布均匀度：

式中：E 为站网分布均匀度；fi为第i 个雨量站的泰森多边形面积为各雨量站泰森多边形面积的平均值；F 为流域总面积；n 为雨量站个数。

2.3 面雨量计算误差统计

本文选用平均绝对误差和均方差度量面雨量误差。平均绝对误差（Mean Absolute Error，MAE）反映了理论值偏离真实值的大小，给出了可能的误差范围。均方差（Mean Square Error，MSE）反映了利用实测站点数据计算面雨量的灵敏度，估计了理论值与真实值系列的拟合程度。二者的计算公式如下：

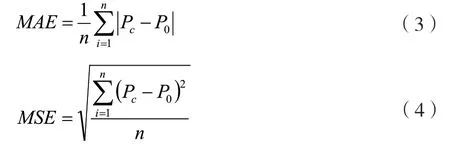
式中：Pc为面雨量理论值；P0为面雨量真值；n 为降雨系列个数。

2.4 关系分析

2.4.1 面雨量误差与站网密度关系

统计5 种站网密度下1956—2016年面雨量的平均绝对误差与均方差，作站点个数与误差关系图，见图1。可以发现，站网密度对面雨量误差有显著影响。当参与面雨量计算的站点个数由55 个减为45 个、35个时，站网密度变化对面雨量误差大小的影响较小，但当站点个数由35 个站减小到25 个站时，面雨量平均绝对误差和均方差随站点个数的减少呈明显的增大趋势，站点由25 个站减小到15 个站时，误差增大幅度最大，说明站点个数减为15 时，无论站点如何分布，都很难捕捉较为准确的降雨空间分布信息。

图1 站点密度与面雨量误差关系图

2.4.2 面雨量误差与均匀度关系

为进一步研究面雨量误差与均匀度的关系，利用随机抽样的原理，分别按照55 站、15 站的数量抽取雨量站，各抽取10 次，组成20 种站网分布。统计20 种站网分布的均匀度、MAE、MSE，作不同站网密度下均匀度与 MAE、MSE 的关系图，因均匀度与MAE、MSE 的关系一致，故以MAE 为例进行关系分析。

如图2 所示，按照2 组站网密度，分别统计其组内10 种站网分布均匀度与 MAE 关系，发现MAE随均匀度的增大呈减小趋势，说明站网分布越趋于均匀化，即站网分布均匀度越接近1，其计算的面雨量越合理。此外，站点数量较多时，图中点据较密集，统计的平均绝对误差较小，随着站点数量的减少，图2 中点据较分散，统计的平均绝对误差越大，计算的均匀度的最小值越小，说明站点数量较多时，站网分布均匀度对MAE 的影响较小，即站网密度较大时，均匀度对面雨量误差波动范围影响较小，站点数量较少时，站网分布均匀度对MAE 的影响较大，此时均匀度对面雨量误差波动范围影响较大，虽然分布较均匀可以降低面雨量误差，但因插值所利用的实测资料太少，难以描述准确的降雨空间分布，计算的面雨量误差值仍较大。

图2 站点分布均匀度与面雨量误差关系图

3 结论

站网密度对面雨量计算精度有显著影响，面雨量误差随站点个数的减少呈增大趋势。站网密度增大到一定程度时，面雨量误差变化趋于平缓。

在同一站网密度下，均匀度越大，站网在流域内分布越均匀，面雨量误差值越小。站网密度较大时，均匀度对面雨量误差波动范围的影响较小；站网密度较小时，均匀度对面雨量误差波动范围影响较大■