基于改进蜂群算法的资源实时均衡策略

宋亚欣，陆 潇，卢 碧，王 媛，鲁 敏

（1.武汉大学 电气与自动化学院，湖北 武汉 430072；2.国网湖北省电力有限公司 超高压公司，湖北 武汉 430050）

0 引言

随着市场经济的飞速发展，企业跟进的项目规模越来越大，而项目迭代周期却越来越短，所以经常出现多个子项目并行进展的情况。针对此种情况，若缺少一个合理且智能的人力资源调度策略，可能会造成企业运行效率低下。当前，传统的人力资源调度[1⁃3]管配模式已无法适应复杂的环境现状，且该情况在电力行业表现得尤为明显。因此，电力行业人力资源调度优化问题成为了近年来的研究重点。

群体智能技术[4⁃6]可以大幅提升电力行业人力资源的管控水平，得到了广泛应用。该技术主要依赖于仿生学原理，目前已成为一种主流技术。与其他群体智能算法相比，人工蜂群算法（Artificial Bee Colony,ABC）[7⁃9]具有迭代收敛速度快、参数设置简单等优势，而且其能避免算法陷入局部最优解。因此，本文将蜂群算法引入到电力行业人力资源调度领域，并对其进行优化改进，提出了一种基于改进蜂群算法的人力资源实时均衡模型，从而实现多个项目并行情况下的人力资源最优调配。

1 人力资源实时均衡模型设计

1.1 人力资源均衡问题建模

电力企业在运行过程中，通常会存在多个项目并行进展的情况。为合理调配人力资源，实现企业效益的最大化，本文综合考虑资源调配过程中的项目数量、各项目下的活动数量、人员数量与薪资等因素，以项目所需人力成本和项目延期惩罚成本最低作为人力资源调度优化问题的目标[10⁃12]，建立如下模型：

式中：f1是基于人力成本的目标函数；f2是基于项目延期惩罚成本的目标函数；xk,t,i,j表示在t时刻，第i个项目的第j个活动由员工k执行；Li表示第i个项目超过计划工期的持续时间；N表示项目总数量；Mi表示第i个项目的活动总数量；MR表示企业当前可分配的人员总数量；Ck表示项目i超出项目规定工期后的惩罚总费用；TCi则表示项目i所需的固定总费用。此外，通过3 个约束条件对参与活动的员工数量和活动的起止时间进行了合理限制，保证了算法的可靠性。

1.2 人工蜂群算法

人工蜂群算法是一种群体智能算法，由Karaboga 于2005 年提出，其通过模拟自然界中蜂群采蜜的一系列群体行为，如蜂群间的信息共享交流、采蜜过程中的分工安排等，来实现采蜜活动的高效化和智能化。

近年来，人工蜂群算法被广泛用于解决人力资源调度优化问题。算法通常包含4 个组成因子，分别为蜂蜜源、引领蜂、跟随蜂和侦查蜂，对应到优化模型中，蜂蜜源表示目标函数的可行解，其质量由可行解的适应度表示。整个目标函数求解的过程对应为蜂群不断地选择优质蜂蜜源，并对劣质蜜源进行淘汰，最终找到邻域内的最优蜜源，即目标函数的全局最优解。此外，根据不同蜜蜂在寻觅蜜源过程中的不同分工，引入了人工蜂群算法的另外3 个组成因子。

设最优化问题的可行解为一个T维向量Yi=，T表示参数的数量。记蜂蜜源的数量为mfood，则可行解域为S={Y1,Y2,…,Ymfood}。基于此，该算法的流程可划分为4 个阶段。

1）初始化蜂蜜源

在可行解域范围内，以随机的方式生成mfood 个T维向量，并对每个向量即每个蜜源的适应度值进行计算，公式如下：

2）引领蜂阶段

对于搜索区域内的蜜源，引领蜂采用贪婪机制[13⁃14]对蜜源进行选取。引领蜂以当前所在的蜜源为基础，通过扩展邻域不断获取新的蜜源，公式如下：

式中：new-yi为引领蜂搜寻到的新蜜源；yi为引领蜂当前所在蜜源；yk为邻域内的其他蜜源；j则代表向量维度。通过引入参数φ对引领蜂的搜索范围进行控制，从而在一定程度上修正蜂群算法的收敛速度。

3）跟随蜂阶段

在跟随蜂阶段，基于上一阶段的蜂源选择结果，跟随蜂通过轮盘赌[15]的方式，以一定的概率选择所要跟随的引领蜂，其概率的计算公式如下：

式中：fiti表示搜索区域内每个蜂蜜源Yi的适应度，适应度值越大，则被跟随蜂选择开采的概率越大。

4）侦查蜂阶段

在搜索区域内，当优质蜜源多次未进行更新时，为避免算法陷入一个局部最优解，侦查蜂便通过式（7）生成新蜜源，以对当前局部最优蜜源进行更新。

1.3 人工蜂群算法改进

传统的人工蜂群算法在蜂源搜索、跟随选择等方面存在一定的盲目性。当需要处理的数据量较大时，对应的算法计算量也随之增大，故而难以满足求解实时性的要求。

为进一步提升算法性能，并改善传统算法容易过早陷入局部最优解的不足，本文对基础蜂群算法进行了三方面改进。

1）引领蜂搜索阶段改进

在基础人工蜂群算法中，由式（7）可以发现：引领蜂在其所在邻域内对新蜜源进行搜索时，搜索范围由参数φ确定，φ为[-1，1]之间的任意值，故引领蜂对于新蜜源位置的选取具有盲目性；同时随机选取的方式还会增加算法的计算量，大幅降低算法的收敛速度。基于此，在引领蜂搜索阶段，本文引入当前最佳蜜源位置Ybest=和等距控制参数，其中等距控制参数公式如下：

式中g为当前的迭代次数。对于任意蜜源位置Yi，根据式（10）分别在搜索区域内生成蜜源位置Vi=此后，依托于当前最优蜜源位置Ybest，从Yi、Vi、Ui中选择最优蜜源进行更新。蜜源更新公式如下所示：

式中β为引入的等距控制参数。

2）跟随蜂搜索阶段改进

在基准蜂群算法中，跟随蜂在选择所要跟随的引领蜂时，通常采用轮盘赌的模式。在轮盘赌模式下，质量好的蜜源被选中的概率较大，反之，质量稍差的蜜源则会被直接抛弃，因此基准算法较易陷入局部最优。为解决这一问题，引入排序选择策略，用于替代基准算法中的轮盘赌模式。该策略的具体实现为：首先根据引领蜂选取的蜂源质量进行优劣排序，之后再依据式（12）和式（13）分别计算出选择排序为k的引领蜂的概率，概率计算公式如下：

式中：nGB为蜂群中引领蜂的数量；Gmax表示最大迭代轮次；a（g）为调节参数。

3）侦查蜂搜索阶段改进

基准蜂群算法中，当引领蜂多次未更新优质蜜源时，侦查蜂便在全体解域内进行搜寻。这种方式在一定程度上避免了算法陷入局部最优解，但降低了算法寻优的效率，导致算法实时性较差。针对该问题，文中在侦查蜂搜索阶段提出了一种基于蜜源浓度的全局更新策略，即侦查蜂在搜集优质蜜源时，按照蜜源浓度的高低有选择性地对新优质蜜源的位置进行搜寻。改进策略公式如下所示：

式中γj为向量第j维解空间的搜索权重。

综上所述，本文所提出的改进蜂群算法的整体实现流程如图1 所示。

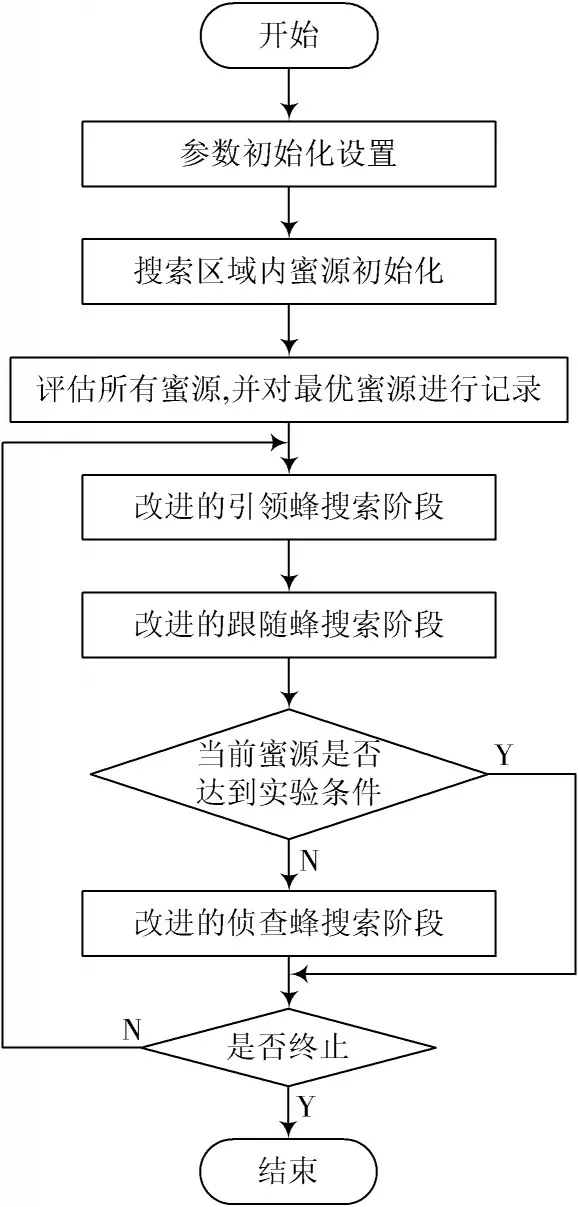
图1 改进蜂群算法的实现流程

1.4 算法模型

针对电力企业人力资源调度优化求解问题，在对模型进行求解的过程中，为满足实时性和准确性要求，对基准蜂群算法进行了改进，提出一种改进的蜂群算法，用于多目标数学优化模型的求解，实现人力资源的实时均衡调度。本文基于改进蜂群算法的人力资源实时均衡模型示意图如图2 所示。

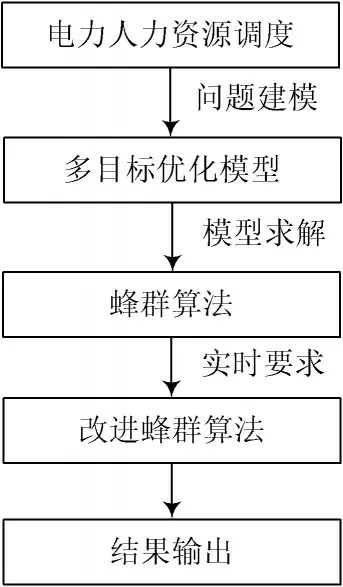
图2 改进算法的模型

2 实验与分析

2.1 数据集和运行环境

本文实验数据来源于湖北省某地区的电力工程项目管理数据集，数据集中包含了工程项目的任务、任务所需的工种、每项任务所需花费的工时以及任务时间约束和成本等相关信息。人力资源数据选择某电力工程项目团队数据，共有员工50 人，包含多个工种。本文算法与对比算法均使用Python 进行编程，算法运行的软硬件环境如表1 所示。

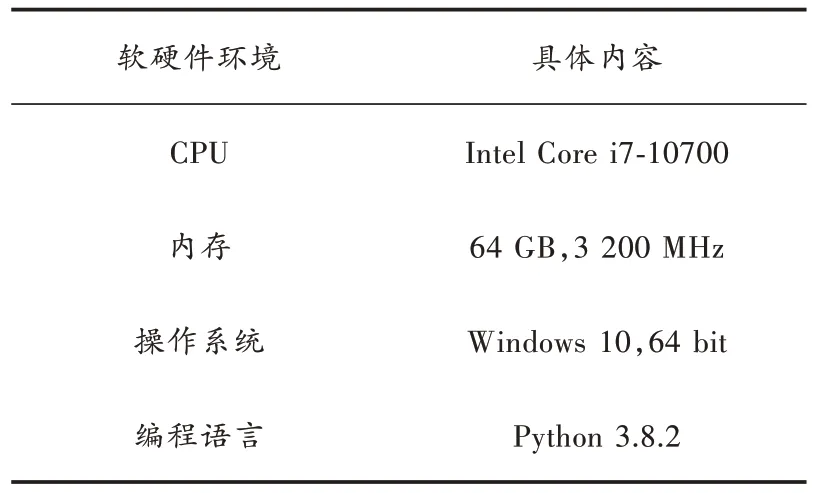
表1 算法运行环境

2.2 算法测试

为了对所提算法的性能进行验证，本次实验测试从数据集中选取若干数据作为训练集，剩余的作为验证集，数量比例为4∶1。

本文算法可对原算法易陷入局部最优解及实时性差的不足之处进行改进，因此在进行迭代实验时，将原算法作为对比算法。实验中的自适应迭代误差设置为0.01，最大迭代次数设置为400，实验结果如图3 所示。

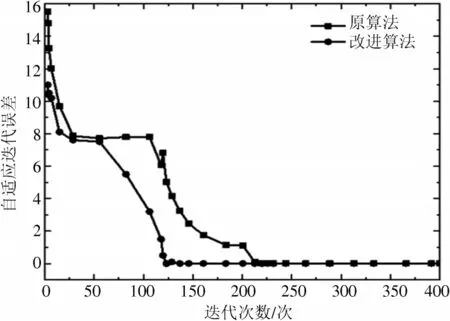
图3 两种迭代实验结果

在图3 中，纵轴表示自适应迭代误差，横轴表示迭代次数，当自适应迭代误差趋近于0.01 时，表示求得最终解。可以看出，原算法迭代次数为200，文中改进算法迭代次数为120，说明本文算法迭代次数较少且迭代时间短，实时性更强。

为验证本文算法的有效性，随机抽取3 个电力工程项目作为标准算例，对比算法选择常见的资源优化与均衡算法（ABC）、蚁群算法（Ant Colony Optimization,ACO）、粒子群算法（Particle Swarm Optimization,PSO），算法性能指标使用目标函数的总人力成本和项目完工时间作为评估项次。算法所得测试结果如表2 所示。

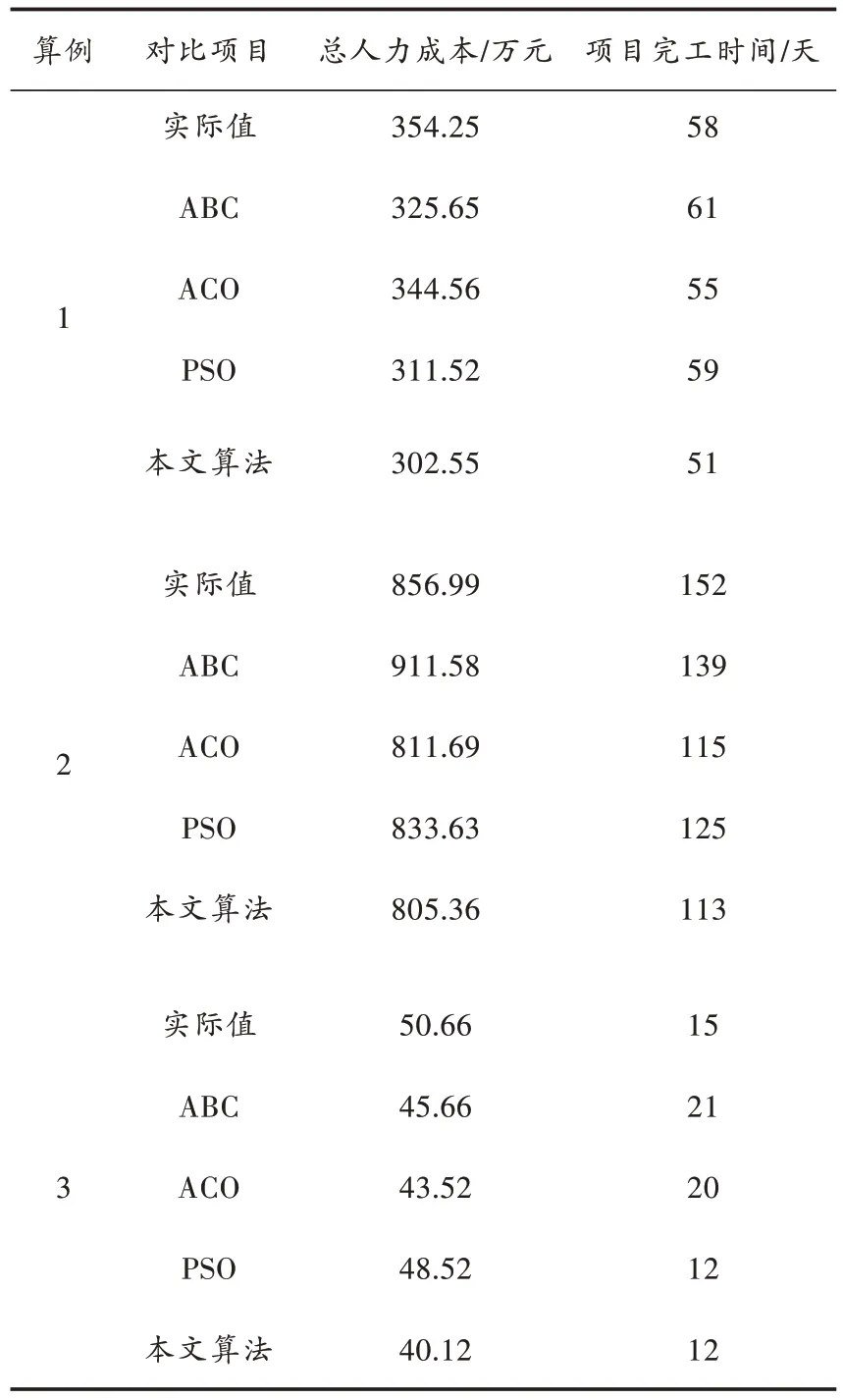
表2 算法测试结果

从表2 中可以看到，各算法均可对电力工程项目涉及到的人力成本及时间进行优化。其中，本文算法在不同人力成本和周期的项目中综合实力表现最优，总人力成本以及项目完工时间相比于其他对比算法最少。由此表明，本文算法的性能出色，对于原算法的改进也是有效的。

3 结语

本文针对传统人力资源均衡算法复杂场景调度能力差的不足，基于改进的蜂群算法提出了一种时间和成本均衡优化的人力资源分配策略。针对传统蜂群算法中存在的缺陷，在算法的3 个阶段进行改进，大幅提升了算法的实时性。在实验测试中，本文算法迭代次数少，相较于其他对比算法具有最优性能，充分表明了改进算法可以提升电力工程人力资源调度效率，进而降低企业人力成本。