CEV模型下保险公司的最优不动产投资及再保险问题

李国庆，田琳琳

(东华大学 理学院,上海)

保险公司增加利润的重要手段之一即投资,再保险则是帮助保险公司规避或转移过度风险的关键。因此,再保险与投资成为保险精算的热门话题。随着持有的市场份额不断增长,保险公司的索赔风险大幅提升。金融市场上的风险资产的波动以及不可预测的风险为主要风险来源。

在保险公司的经典投资问题中,Browne[1]利用扩散风险模型研究了保险公司最终财富效用最大化和破产概率最小化的问题。Bai等[2]用多维几何布朗运动描述股票市场,在终端指数效用最大化下得到了最优投资策略。而对于金融市场的风险资产来说,其波动率不是常数,因此常弹性方差CEV模型逐渐被运用到股票价格中。Gu等[3]和Liang等[4]在跳-扩散风险过程中,分析了CEV模型下的最优比例再保险与投资问题。Gu等[5]研究了盈余过程为带漂移的布朗运动时,CEV模型下的超额-损失再保险策略。Wu等[6]也研究了CEV模型下的再保险与投资策略。

近年来,不动产投资业务逐渐进入了保险公司的视野。在一定程度上,投资不动产可以缓解金融市场波动对收益率的影响,有利于提高保险公司资产与负债的匹配度。但不能在无策略、无限制的方式下进行不动产投资,否则可能会面临巨大风险。目前,关于不动产投资的研究大多停留在定性论述的层面,量化研究还是相对匮乏。

Decamps等[7]为了提高公司单位时间现金收益,考虑投资于新技术项目,其目标为最大化期望累积分红。Miao等[8]则在效用最大化框架下考虑了不动产投资问题,并假定该投资可以实现随机收益。但以上研究并没有考虑同时投资金融市场与不动产项目的情形。

假设保险公司同时投资于基金、股票和不动产,其中风险资产的价格由CEV模型决定。除去金融市场的投资外,保险公司还通过购买一定比例的再保险来转移因保险索赔而产生的部分风险。为了保险公司的财富最大化,采用终端指数效用函数去描述其趋势,建立Hamilton-Jacobi-Bellmam (HJB)方程并求解,通过验证定理验证HJB方程所得到的解是最优控制问题的解,并利用数值实例探讨最优策略的性质。

1 保险公司收益模型与金融市场

首先,假设在金融市场上资产可以持续交易,交易中不涉及税收与成本。设(Ω,,t,P)是完全概率空间,其中P表示概率测度,t表示到时刻t为止所有获得的综合信息,时刻t的决策基于信息流{t;t∈[0,T]}给出,且满足通常条件(即为右连续且P-完备的),交易可在时间t∈[0,T]发生,T<∞是终端时刻。

经典的Cramér-Lundberg风险财富过程模型服从随机微分方程式(1)：

(1)

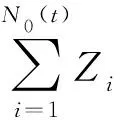
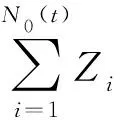
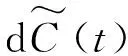
(2)

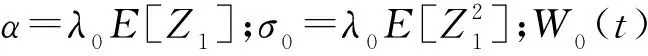
dR1(t)=αμdt+σ0dW0(t)

(3)

假设保险公司可以通过购买一定比例再保险来控制风险。对任意时间t∈[0,T],设保险公司以q(t)的比例购买再保险,且q(t)∈[0,1]。假设再保险公司使用期望保费原则,即保费率为α(1+θ)q(t),其中θ>μ代表再保险公司的安全负荷。因此,在存在比例再保险条约的情况下,保险公司的盈余过程为

(4)

假设金融市场有债券资产、股票资产和不动产3种资产可用于投资。设债券资产S0(t)的价格过程满足

dS0(t)=r0S0(t)dt

(5)

式中：r0>0表示债券资产的利率。设股票资产S(t)的价格过程满足CEV模型,如式(6)所示。

dS(t)=r1S(t)dt+σ1Sβ+1(t)dW1(t)

(6)

式中：r1>0为股票资产的收益率;σ1为股票资产波动率;-1<β<0为弹性因子;W1(t)为标准布朗运动。Chen等[10]最早提出用跳-扩散模型描述不动产资产价格,其价格过程S2(t)为

(7)

式中：r2>0为不动产资产的收益率;σ2为不动产资产波动率;{N(t),0≤t≤T}为强度为λ>0的泊松过程;{Ui,i≥1}为一个正且独立的随机变量序列,用于描述无法预期的冲击;W2(t)为标准布朗运动;泊松过程N(t)与布朗运动W2(t)相互独立,且泊松过程N(t)分别与前文W0(t),W1(t)独立。由于不动产资产会带来房租收益,Sing[11]最早提出房租收益模型,且房租收益过程S3(t)满足

dS3(t)=S2(t)[r3dt+σ3dW3(t)]

(8)

式中：r3>0为租金与房价比;σ3>0为房租收益的波动率;W3(t)为标准布朗运动,且W3(t)与泊松过程N(t)独立。

按照“偿二代”的风险测算体系,权益类金融产品有比不动产更高的风险因子,根据金融理论,风险因子越高,收益也应越高,因此有r1>r2>r0,σ2<σ1。假设股票资产的风险与不动产资产的风险独立,而房地产价格过程和房租收益过程存在强相关关系。从而有W1(t)与W2(t)相互独立,W1(t)与W3(t)相互独立,W2(t)与W3(t)正相关,其相关系数为ρ。

假设保险公司将全部收益进行投资,a(t)为投资于股票资产的金额,b(t)为投资于不动产的金额,其中在任意t∈[0,T]时b(t)≥0,即在任何时候不动产投资不可以出现卖空的现象。剩余收益用于投资债券资产,则公司财富过程X(t)满足式(9)。

(9)

分别将(4)～(8)代入式(9)得到公司的财富过程为

dX(t)=[(μ-θq(t))α+X(t)r0+a(t)(r1-r0)+b(t)(r3+r2-r0)]dt+

(10)

假设保险公司可以动态购买比例再保险并投资于上述金融市场。区间[0,T]上的交易策略由三维随机过程π=(q(t),a(t),b(t))表示。称策略π为可行策略,若其满足π=(q(t),a(t),b(t))是[t]t∈[0,T]循序可测的且满足用Π表示所有可行策略形成的集合。

2 指数效用与HJB方程

假设效用函数具有如下指数形式：

(11)

将值函数定义为

(12)

根据随机最优控制理论,得到HJB方程如式(13)所示。

(13)

3 HJB方程的解与验证定理

求解HJB方程的解以及最优控制策略π*,通过验证定理证明HJB方程的解析解是最优值函数v(t,x,s)。

首先,假设HJB方程具有经典解,最优策略根据HJB方程一阶最大化条件给出。

(14)

将式(14)代入式(13)可得：

(15)

设式(15)的解为

(16)

式中：m>0,且有边值条件f(T)=1,g(T)=0,z(T)=0。

分别对t,x,s求一阶与二阶偏导,并用矩母函数表示E(V(t,x+bU,s)-V(t,x,s))

(17)

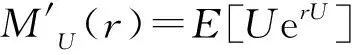
(18)

易知使式(18)成立的b为式(19)的根。

(19)

当b=0时,式(19)左端小于0;当b趋向于无穷时,式(19)左端亦趋向于无穷,且式(19)左端关于b单调连续。因此式(19)存在唯一的正根,记b0(t)为式(19)的唯一正根。给定随机变量U的分布,可以对b0(t)的闭式表达式进行数值模拟,因此式(15)可化为

(20)

消除对x与s的依赖性,考虑边值条件f(T)=1,g(T)=0可解得

(21)

将式(21)代入式(20)

(22)

结合边值条件z(T)=0,U的分布及b0(t),可以求解微分方程式(22),将其解记为z0(t)。

将以上结果代入式(14)计算可得

(23)

b0(t)满足

(24)

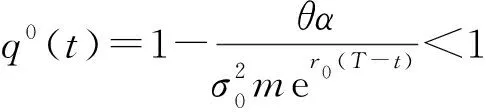
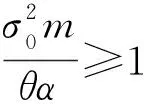
q*(t)=q0(t),a*(t)=a0(t),b*(t)=b0(t),t∈[0,T]

(25)

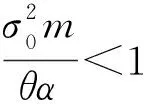
(26)

将q*(t)=0代入式(13)得

(27)

其中

(28)

将式(28)代入式(27)得

(29)

式(29)与式(15)解的构造形式相同,则其偏导数也与式(17)相同,分别代入并化简得

(30)

同理有

(31)

消除对x与s的依赖性,并考虑边值条件f(T)=1,g(T)=0可解得

(32)

将式(32)代入式(31),计算得

(33)

连同边值条件z(T)=0,记解为z1(t),将以上结果代入式(28)计算得

(34)

b1(t)满足

(35)

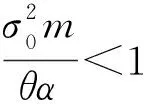
(36)

(37)

其中b0(t)满足

b1(t)满足

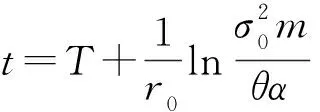
综上所述,HJB方程式(13)的解与最优策略如下：

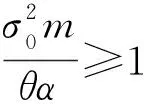
HJB方程的解V(t,x,s)为

(38)

式中：f*(t)=f0(t)、g*(t)=g0(t)、z*(t)=z0(t)。

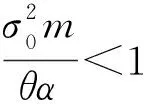
HJB方程的解V(t,x,s)为

(39)

式中：f*(t)=f1(t),g*(t)=g1(t),

定理1由式(38)与式(39)给出的HJB方程的解是最优控制问题式(12)的值函数,即v(t,x,s)=V(t,x,s)可知,最优控制策略为π*=(q*(t),a*(t),b*(t))。

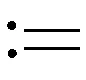
(40)

其中算子

根据Bremaud[12]可知

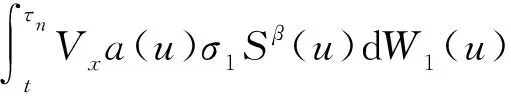
利用BDG不等式可得

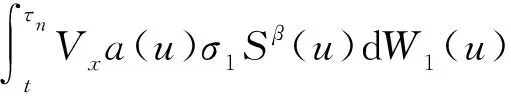
对式(40)两端同时取条件期望可得

E[V(τn,X(τn),S(τn))|X(t)=x,S(t)=s]=V(t,x,s)+

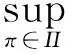
易知V(τn,X(τn),S(τn)),n=1,2,……是一致可积的,因此

当控制策略取π*时,不等式变为等式,即v(t,x,s)=V(t,x,s),可得π*为原优化问题的最优策略。

4 数值模拟

对最优控制策略π*=(q*(t),a*(t),b*(t))进行数值分析。设Z服从均值为0.5,方差为0.25的正态分布,U服从均值为2,方差为1的正态分布,且λ0=1,终端时刻T=3,模型的其余参数假设如下：

θ=0.3,μ=0.2,β=-0.5,r1=0.5,

r2=0.4,r3=0.3,σ1=0.3,σ2=0.2,

σ3=0.1,ρ=0.8,m=1,λ=1。

对于再保险策略q*(t),得到的结果与经典比例再保险策略类似,随着时间t增加,再保险比例逐渐降低,并且降低速率逐渐增长。取不同参数r0=0.2、r0=0.3时可知,当债券资产的利率更大时,初始时刻的再保险比例也越大,且下降速率更快,而终端时刻再保险比例达到相同,如图1所示。

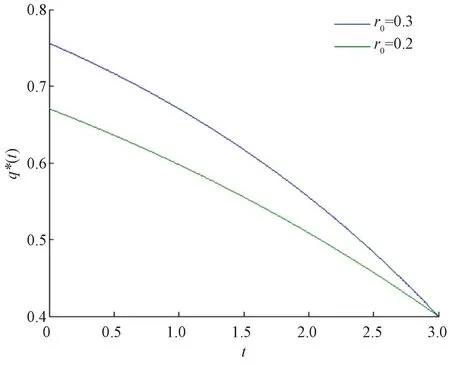
图1 债券利率对再保险策略的影响Fig.1 Influence of bond interest rate on reinsurance strategy

对于股票资产投资策略a*(t),由于股票资产满足CEV模型,因此其与股票市场价格息息相关,分别取s=1、s=2可得知股票资产价格上涨,投资力度更大。同样的,随着时间增加,投资力度也越大,如图2所示。

图2 股票价格对股票投资策略的影响Fig.2 Influence of stock prices on stock investment strategy

对于不动产投资策略b*(t),其策略走向与股票资产类似,投资策略依然满足随着时间的增加投资力度也增大,如图3所示。

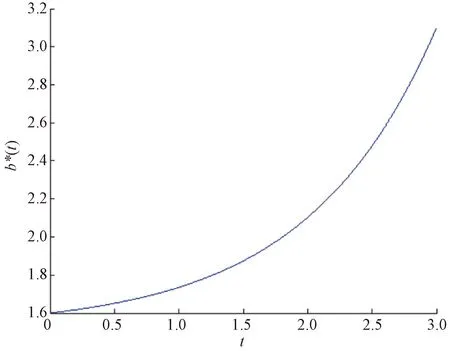
图3 不动产投资策略Fig.3 Real estate investment strategy

5 结 语

在债券,股票及最优再保险的投资组合基础上,分析不动产及出租该不动产所获得的随机收益模型,以最大化终端效用为目标研究了保险公司最优投资组合。研究结果表明：时间、利率、股票价格等因素均会影响到保险公司的终端效用。从经济学的角度,随时间变量的增加,保险公司更倾向于承担更多索赔风险,进而获得更多保费,同时对于固定资产的投资量也会增加,从而在终端获得更大效用值。随着股票价格的增加,增加股票头寸可以获得更多的投资收益。此外,当利率增加时,保险公司应适当降低自留风险,增加对于无风险资产的投资,从而提高终端效用。