布料包装设备中翻折机构的结构设计与运动分析

2024-02-29孙志宏

东华大学学报（自然科学版） 2024年1期

李彬，孙志宏，b

(东华大学 a.机械工程学院,b.纺织装备教育部工程研究中心, 上海)

公理化设计(axiomactic design, AD)理论[1]通过运用科学严谨的设计公理与方法,为结构方案的设计与评估指明依据。韩军等[2]采用公理化设计理论结合层级映射关系获得可行的设计参数,实现了对设施蔬菜种植微小型旋耕机造型的创新设计。唐峰等[3]在设计用于鞭炮产品的机构中,以公理化设计理论为出发点,建立功能模块并分析其中的映射关系,结合成本控制的方法规范了产品设计流程,节省了成本。房德磊等[4]利用公理化设计原理,从概念设计出发分析设计过程中的耦合情况,并对结构模型进行仿真分析,设计出一款适用石油水平井特殊条件下的全液压驱动管道机器人。但目前在纺织机械领域的产品设计中极少采用公理化设计方法进行机构设计或优化分析,故本文以公理化设计方法为指导,开展布料包装设备中翻折机构设计与分析。

1 公理化设计概述

作为新的概念性设计理论,AD理论提出了设计域的概念,通过划分用户域、功能域、结构域和工艺域等4个设计域来剖析整个设计流程[5]。4个设计域对应的元素分别为用户需求(customer attributes,CAs)、功能要求(functional requirements,FRs)、设计参数(design parameters,DPs)和过程变量(process variables,PVs)[6]。因此,产品设计为公理化设计4个设计域的映射过程,如图1所示。按实际设计需要生成设计层级树,以功能特性和结构特性设计的复杂产品方案进行案例分解,得到不同设计层次的设计需求[7]。设计层级树可清晰地描述出功能设计域和结构设计域的设计目的,如图2所示。

图1 公理化设计域映射过程Fig.1 Axiomatic design domain mapping process

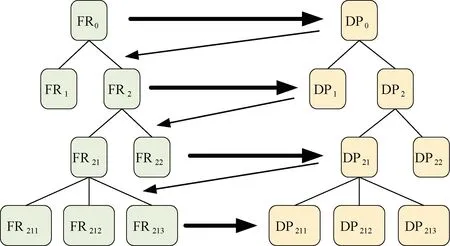
图2 功能特性与结构特性层级树Fig.2 Hierarchical tree of functional and structural properties

AD理论的重点内容包含了独立性公理和信息公理,可用来指导复杂产品的方案设计[8]。独立性公理是指在FRs满足相互独立的前提下,DPs与其他的 FRs 不存在耦合牵连关系[9]。信息公理是以独立性公理为前提,在不同设计方案中所含信息量最少的设计是最优设计[10]。

2 翻折机构概念化设计分析

2.1 翻折机构多级域设计分析

翻折机构是纺织产业链中布料经染整工序处理后的一种包装设备,用于实现布料的运输、贮藏以及进一步加工。用户(企业)提供了包装布料的幅宽范围和最重的质量,并对布料包装提出要求。翻折机构配合码布机(为计量布料总长,利用码布机上摆杆来回1 m摆动将布料层叠码放)进行布料的包装(布料参数：幅宽为1.4～2.2 m,布卷质量为小于30 kg),既要保证操作的安全与稳定,同时需依据现有的生产方式进行设计,由此列出企业需求指标如表1所示。

表1 用户需求明细Table 1 Breakdown of user requirements

本文将用户需求定义为“使用布料包装翻折机构”,将第一层级功能需求“翻转折叠”设定为FR,用“翻折机构”实现前述需求,设定为DP。基于设计目标,翻折机构具有提供翻折动力、避免工作干涉、满足舒适性和实现翻折4项基本功能。为实现该4项基本功能,第二层级系统设计对应功能需求的设计元素包括运动输出单元、对称翻折结构、舒适的工作台高度以及翻折元件。其中完成翻折功能要求又可分为满足不同的布料幅宽与翻折过程平稳,故设计域第三层对应功能域第三层为可伸缩元件与运动特性的要求。功能域与设计域的各个层级对应元素分析完成如表2所示,两者的映射关系如图3所示。

表2 功能域与结构域元素Table 2 Elements of functional and structural domains

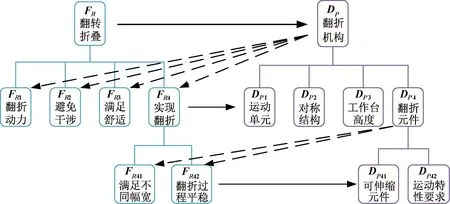
图3 功能域与结构域层级映射关系Fig.3 Functional domain and structural domain hierarchy mapping relationship

2.2 机构设计耦合分析

用产品设计方程表示公理化设计域间层次结构中某一层级的功能需求与该层设计域中的设计参数之间的关系[11],如公式(1)所示：

或{FR}m×1=Am×n{DP}n×1

(1)

式中：{FR}m×1为功能需求向量;{DP}n×1为设计参数向量;Am×n为产品设计矩阵。

根据设计矩阵的不同结构形式可分为3种类型,其与独立性公理的关系如表3所示。

表3 设计矩阵与独立性公理关系Table 3 Design matrix and independence axiom relationship

本研究的翻折机构的功能域与结构域：第一层为单元素的映射过程(见图3),属于非耦合独立设计;第二层功能域到结构域映射关系如式(2) 所示;第三层映射关系如式(3) 所示,设计矩阵非零元素都在对角线上,即第二层和第三层的功能域与设计域之间属于非耦合设计,满足独立性公理。

(2)

(3)

式中：1为强相关;0为弱相关或不相关;

由式(2)、(3)可知,布料包装设备用的翻折机构设计属于非耦合设计,符合独立性公理,其每个设计细节都是设备设计与生产的理论指导。翻折机构的结构设计方案：凸轮作为运动输出单元来提供翻折动力,配合推杆连接翻折连杆和翻折板构成两侧对称结构以避免翻折工作中的干涉问题;限定整个机构垂直方向高度来满足操作的舒适性要求;针对不同布料幅宽采用伸缩杆来进行适配;对翻折板的转角、角速度和角加速度进行具体的设计分析,以保证翻折过程平稳。布料包装设备用的翻折机构工作过程：通过电机驱动凸轮转动,在推程阶段,推杆向上运动并连接翻折连杆实现翻折板相对转动,完成布料的翻折;当凸轮运转到回程阶段,推杆向下运动,翻折板相背转动处于复位阶段直至回到初始状态,此过程中翻折板与布料脱离;凸轮处于休止阶段时,人工对布料的翻折效果及设备运转状态进行审查。

3 翻折机构结构设计分析

在满足公理化设计准则的前提下,本文设计的翻折机构具体用于布料包装领域,以弥补该领域的欠缺。该翻折机构选用凸轮机构使得从动件实现间歇往返运动,再串联连杆机构完成工作,整体机构示意如图4所示。

图4 翻折机构示意图Fig.4 Diagram of folding mechanism

整个机构由翻折凸轮、Y字推杆、翻折连杆、翻折板和伸缩杆组成。凸轮运动可实现两侧翻折板对向运动,以完成布料的翻转与折叠。翻折板上安装的伸缩杆可适应不同幅宽的布料。翻折机构左右两侧为对称结构,因此只选取右侧结构进行设计分析。由图4可知,翻折机构为由凸轮机构和曲柄滑块机构串联而成的六连杆机构,其中滑块行程距离即为凸轮从动件的推程高度。综上所述,本文先设计曲柄滑块机构相关结构,再确定凸轮机构中从动件的运动规律来设计凸轮机构。

3.1 曲柄滑块机构设计

以右侧结构翻折板转动中心为原点建立直角坐标系,转动中心到翻折连杆铰接点的连杆为OA,翻折连杆为AB,Y字推杆转换为滑块,故翻折机构中连杆机构即等效为曲柄滑块机构,如图5所示。给定OA杆长为l1,AB杆长为l2,OA、AB与x轴正向夹角分别为φ1、φ2,偏距(曲柄回转中心与滑块移动导路的偏置距离BC)为e,OC杆长为l,其中Ai与Bi(i=1,2,3)为3个不同时刻A点与B点位置之间的3组对应关系。

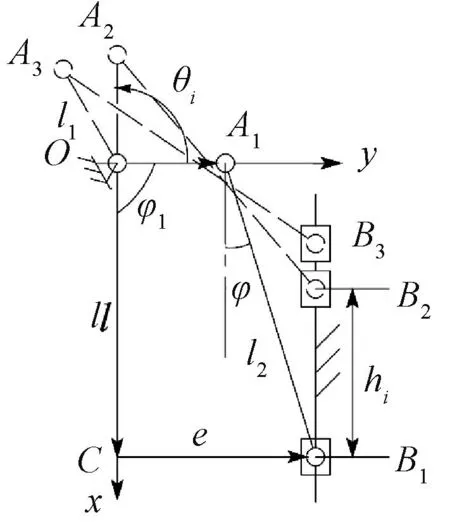
图5 曲柄滑块机构示意图Fig.5 Crank slider mechanism schematic

由封闭四边形OABC各矢量方向得封闭矢量方程如式(4)所示。

(4)

分别取实部和虚部得：

(5)

由式(5)可得

(6)

故B点坐标为

为探究翻转板转动角度与布料位置状态的关系,本文以翻转板转动90°为起点,依次增加5°(直至120°)进行试验,相关试验结果如表4所示。由表4可知,当转角大于115°时可实现布料的翻折。

表4 翻转板转角与布料状态关系Table 4 Turning angle of floding plate and fabric state relationship

结合整机尺寸高度设定翻折板转角θi与推杆位移hi(i=1,2,3)之间的3组对应关系：θ1=0,h1=0 mm;θ2=π/2,h2=79.97 mm;θ3=2π/3,h3=159.94 mm。如图5所示,A1B1、A2B2、A3B3分别为翻折连杆的3处位置,而θi为OAi与y轴正向的夹角。

利用位移矩阵法[12-13],得出OA的位移矩阵

(7)

则A点的位置方程为

(8)

而B点做上下往复运动,其坐标方程为

(9)

且AB杆长不变,故由定长条件,得约束方程

(Aix-Bix)2+(Aiy-Biy)2=

(A1x-B1x)2+(A1y-B1y)2

(10)

企业生产过程中,包装前的面料须经码布机进行前处理,而码布机最终的出料平台距离地面750 mm,该高度符合企业操作工人搬运习惯,因此设为布料折叠包装机承接布料的高度,即机构空间配合高度OA=60.0 mm,联立式(7)～(10),解得翻折连杆AB为300.0 mm,滑块偏距By为240.0 mm。

3.2 凸轮廓线设计

结合实际生产工况要求,机构适用于中高速匀速重载,实现布料翻折时间为1～2 s,故设定翻转凸轮的转速为25 r/min,且逆时针转动。凸轮机构在推程阶段实现布料的翻折,而回程阶段则为机构的复位。为提升工作效率,凸轮机构回程阶段时间不应过长,同时增加休止阶段来完成布料翻折效果与设备运转状态的审查工作,按表5所示分配凸轮转角与从动推杆的运动行程关系。

表5 凸轮转角与运动相位配合关系

在推程阶段,需保证布料不因受到冲击而散落,因此在凸轮给恒定转速的情况下选用几种常见的凸轮从动件运动规律来研究翻折板的运动情况[14]。图6和图7为不同凸轮在动件运动规律下,翻折板的角速度与角加速度变化。由图6和图7可知：除等速运动规律外,其余几种运动规律的推程过程中,翻折板的角加速度都发生了变化,且角速度峰值位置位于翻折过程中,这势必会造成布料散落,因此凸轮推程部分选用等速运动规律,翻折过程的翻折板角速度与角加速度变化平稳,更利于布料的翻折。

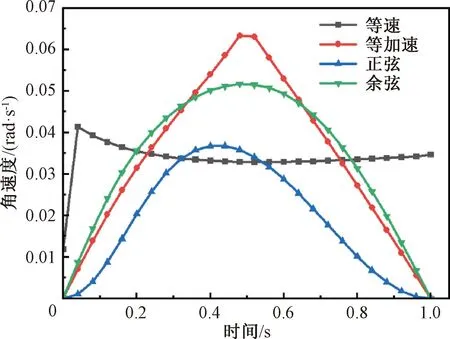
图6 不同从动件运动规律下翻折板角速度Fig.6 Angular velocity of folding plate under different follower motion laws

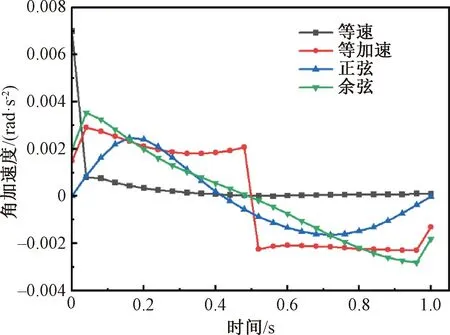
图7 不同从动件运动规律下翻折板角加速度Fig.7 Angular acceleration of folding plate under different follower motion laws

设定凸轮逆时针转动,转动角速度为ω,凸轮转角为δ(弧度制),凸轮推程运动角δ0=5π/6,回程运动角δ′0=2π/3(见表5),推杆上升高度h=160 mm。由于推程阶段存在刚性冲击,因此需在运动始末加以修正,运动回程阶段处于空载情况,对运动特性无特殊要求。为减小冲击,本文在此阶段按正弦加速度运动规律来设计凸轮廓线。

当δ∈[0,5π/6)时,推杆推程的运动方程如式(11)所示。

(11)

当δ∈[5π/6,3π/2)时,推杆回程的运动方程如式(12)所示。

(12)

当δ∈[3π/2,2π]时,推杆处于休止阶段,其位移、速度、加速度均为零。

因布料包装设备整机高度有限,且大尺寸凸轮会消耗更大能量,在满足凸轮机构压力角小于许用压力角的前提下,为更好地设计与装配,设定基圆半径R=100 mm,再利用式(11)～(12)结合反转解析法[15]得到凸轮的轮廓曲线,同时为避免推程始末的刚性冲击,对所绘制的凸轮廓线[16]在运动不同阶段的连接处做修整处理,如图8所示。经修整后,翻折板在推程阶段运行的刚性冲击得到明显改善,推程阶段翻折板修整前后的加速度变化如图9所示。

图8 翻折凸轮轮廓曲线Fig.8 Profile curve of the folding cam

图9 翻折板修整前后的加速度变化Fig.9 Variation of angular acceleration of folding plate during the pushing phase before and after trimming

4 运动仿真分析

创建翻折机构的模型,使用Motion插件进行运动仿真分析[17-19]。其中,Y字推杆与左右翻折连杆铰接点的水平距离为980 mm,且该铰接点至Y字推杆与凸轮的接触点垂直高度为300 mm,其余各构件尺寸根据前述结构设计构建。1个翻折周期即凸轮转动1周,凸轮与推杆为正偏置装配,可以更好地传动。仿真时间设置为2.4 s,可得到翻折板的运动尺度的变化如图10～11所示。

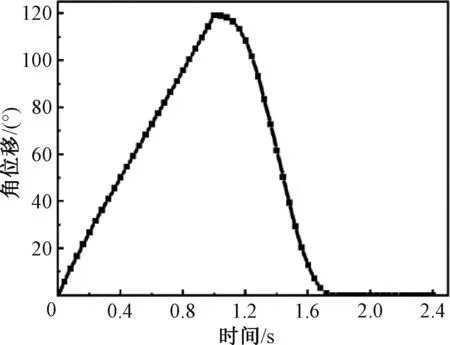
图10 翻折板角位移变化Fig.10 Variation of angular displacement of folding plate

由图10可知,翻折板的角位移随时间变化呈先上升后下降再稳定的趋势,且最大转角位置在1 s处,即凸轮转动150.00°。推程结束翻折板翻转最大角度为119.11°,与设计条件偏差0.74%,这并不影响实际生产,故该机构设计能够实现指定的动作需求。

由图11可知,凸轮的推程阶段除在开始时存在冲击外,其余过程中的翻折板角速度与角加速度均变化平稳;推程结束时角速度和角加速度由于凸轮从动件运动规律变化而产生了突变,此处刚好布料与翻折板脱离,故不会影响翻折效果。回程阶段角速度与角加速度符合正弦运动规律,满足慢进快回的设计要求。因此,该翻折机构的运动特性满足结构设计需求并符合实际生产情况。