深海声影区时频谱干涉结构与声源定位∗

刘与涵 郭良浩 章伟裕 闫 超 董 阁

(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

深海声源定位是海洋声学的重要问题之一。对于近水面深度(1000 m 以浅)的声源和接收点，由于水体声速剖面的折射效应，在几千米至几十千米的水平距离范围内通常会形成海底反射区。该区域内只有经海底反射的声线到达，由于缺少直达声线和水体反转声线，声传播损失较大，也称为声影区。声影区的水平覆盖范围较大，是中近程水声探测的主要区域。

匹配场处理方法较早被应用于深海声源定位。Fizell 等[1]利用垂直阵定位了深海中的低频声源。周士弘等[2]将广义相积分简正波方法用于匹配场定位，以提高深海拷贝场的计算效率。陈连荣等[3]将高斯射线束方法用于深海匹配场定位。但是，匹配场处理方法对于海底底质等环境参数的失配问题比较敏感，且通常需要较大的垂直接收孔径以提高定位精度。

为了提高定位稳健性以及减小接收孔径，国内外学者开展了大量深海声源定位方法研究。Tiemann 等[4]利用单水听器接收信号提取多途时延差，对抹香鲸发出的宽带脉冲声源进行定位。杨士莪[5]通过小型矢量立体阵接收的多途到达角，联合解算声源方位、距离和深度。McCargar 等[6]通过垂直阵的窄带信号波束输出能量随距离变化的明暗干涉周期，估计直达声区内的声源深度。王文博等[7]进一步利用宽带声场的频率-掠射角干涉结构，估计直达声区内的声源深度。

在声影区中，声场由经一次海底反射的多途声线主导，这些声线的到达俯仰角和时延差等多途特征可利用小孔径阵列获取。此外，上述多途参数受海底底质的影响较小，且由于海底反射声线的掠射角较大，声速剖面的不确定性对其影响也较小。因此，利用声影区的多途特征可实现比较稳健的声源定位。Duan 等[8]利用近水面深度的垂直短阵进行窄带观测，通过加权子空间匹配方法进行声源定位。吴禹沈等[9]利用水下滑翔机接收脉冲声信号，通过多途到达时延差进行声源定位。谢亮等[10]通过垂直阵提取脉冲簇到达结构，进行水下声源定位。刘与涵等[11]利用短间距垂直双水听器接收窄带宽信号，通过频谱搬移和稀疏时延估计方法提取多途到达时延差，估计声源距离。

此外，声影区的声场强度在距离-频率维通常会形成比较稳健的干涉结构。Li 等[12]指出，声影区中的波导不变量(β)值接近1，声场的干涉条纹斜率与浅海比较相近。翁晋宝等[13]研究了声影区中的距离-频率干涉结构，发现存在两种干涉条纹，第一种条纹的频率周期与水平距离和声源深度有关，第二种条纹的频率周期与水平距离和接收深度有关。吴俊楠等[14]进一步指出，水面船辐射噪声形成的第一种条纹在较窄的频带内可忽略，通过水平阵波束输出信号的自相关函数，可有效提取第二种条纹的频率周期，估计水面声源的距离。翁晋宝等[15-16]也利用单水听器接收的时频谱干涉结构，验证了上述定位方法的有效性。

深海声影区的传播损失较大，在实际的水声探测中，随着接收信噪比(Signal-to-noise ratio,SNR)降低，现有的声影区定位方法的性能逐渐下降或失效。理论上，对接收信号时频谱进行二维傅里叶变换(Two-dimensional Fourier transform,2-D FT)后处理，可将变换前能量分散的干涉条纹聚焦在变换后能量集中的较小区域内，以提高低SNR 条件下的干涉结构检测能力[17]。但是，现有2-D FT 研究主要关注于浅海环境，针对深海声影区的有关研究较少。浅海声场通常具有多组斜率近似相同的干涉条纹，对应的β值在1 附近，因此2-D FT 幅度谱通常呈现一条“脊”状分布[18]。基于这一特性，Cockrell等[19]利用2-D FT估计浅海声场的干涉条纹斜率，从而解算声源距离。相比之下，深海声影区中的β分布复杂多变，影区声场的特点在于干涉条纹种类较少，对应的2-D FT 幅度谱通常呈“点”状分布，不能直接沿用浅海声源定位方法。因此，有必要进一步研究影区干涉条纹及其2-D FT 幅度谱的分布规律与声源位置的关系，再通过2-D FT 方法提取上述幅度谱分布结构，以实现低SNR条件下的深海声源定位。

本文基于射线理论，在研究深海声影区中水面运动声源形成的时频谱干涉结构的基础上，建立了频率干涉周期与声源距离的关系、时间干涉周期与声源径向速度的关系。通过时频谱的2-D FT 幅度谱提取上述两种时频干涉周期，再通过多频带处理方法提高低SNR 下的检测能力。数值仿真及海试数据处理结果表明，相比于现有的利用接收信号自相关的声源测距方法，所提出的利用时频谱2-D FT的定位方法得到的距离和径向速度估计精度较高，且测距连续性较好，比较适用于低SNR条件下的声源定位。

1 声影区时频谱干涉结构

1.1 干涉条纹形成机理

根据射线声学理论，对于图1(a)所示的典型深海声速剖面，直达声线和水体反转声线无法到达声影区。在第一影区中，经二次及以上海底反射的声线传播损失较大，对声场的影响通常可忽略。经一次海底反射的4 条多途声线对声场能量起主要贡献，分别为海底反射(BR)声线、海面-海底反射(SBR)声线、海底-海面反射(BSR)声线和海面-海底-海面反射(SBSR)声线，其传播轨迹如图1(b) 所示。

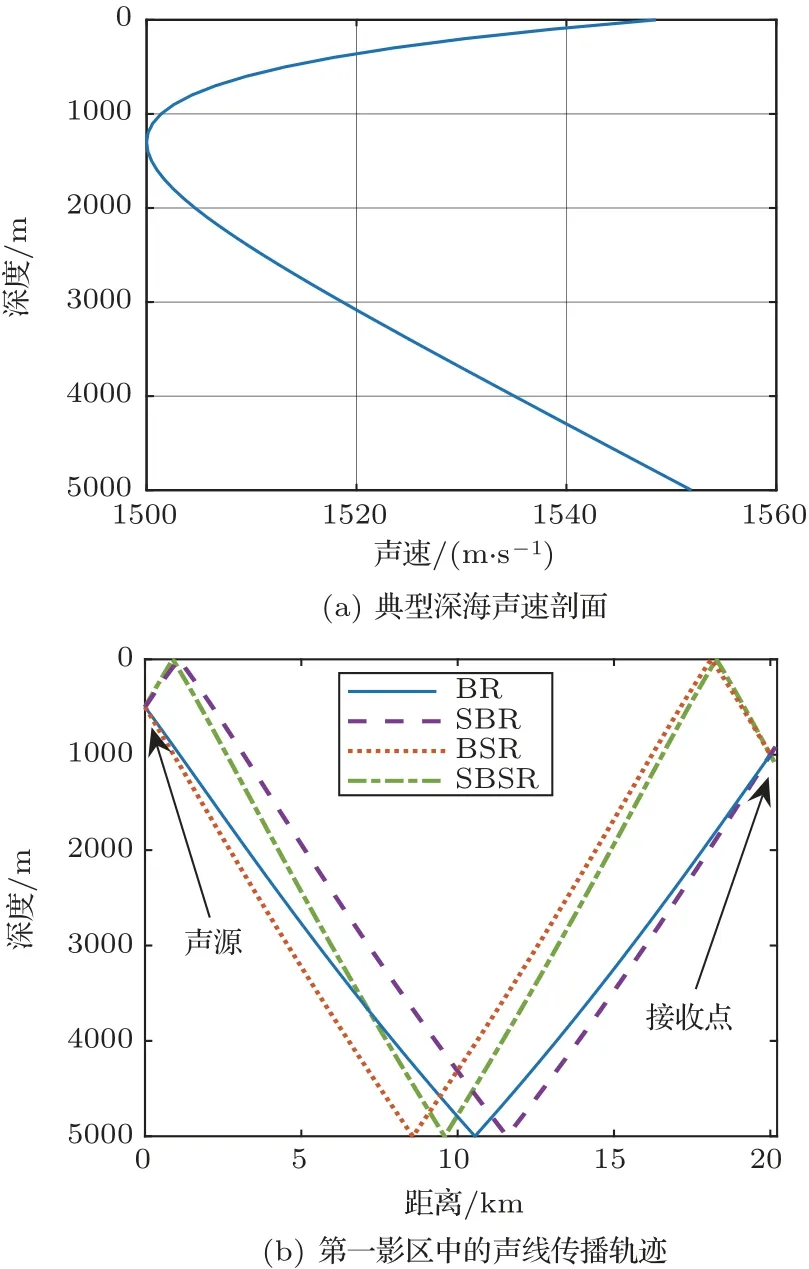
图1 典型深海声速剖面和第一影区中的声线传播轨迹Fig.1 A typical sound speed profile in deep water and the propagation paths of the acoustic rays in the first shadow zone

位于接收点(r,zr)、频率为f的声压可表示为上述多途声线的相干叠加：

其中，r表示水平距离，zr表示接收深度，ti(i=1,2,3,4)分别表示BR、SBR、BSR 和SBSR 声线的到达时延。

因此，声场强度可近似表示为[13]

其中，τ12≡t2-t1为SBR声线与BR声线的到达时延差，τ13≡t3-t1为BSR声线与BR声线的到达时延差。需要说明的是，SBSR 声线与BSR 声线的到达时延差τ34≡t4-t3与τ12近似相等，在推导过程中由τ12替换，因此式(2)省略了与SBSR 声线有关的时延项。

对于水面船辐射噪声，声源深度通常仅为几米，到达接收点的SBR 声线与BR 声线的传播轨迹十分接近，导致τ12通常小于几毫秒。对于500 Hz以下的低频声场，f与τ12的乘积通常小于5。因此，在较窄的频带和较短的观测时间内，式(2)中的cos 2πfτ12项可近似为常数。与之相比，水听器接收深度通常数倍于声源深度，导致τ13也数倍于τ12。因此，式(2)中cos 2πfτ13项的周期变化会形成声场强度的干涉现象。当τ13=n/f，n∈Z+时，声强出现干涉相消；当τ13=(m+1/2)/f，m∈Z+时，声强出现干涉相长。

在实际的被动观测中，接收深度zr通常在一定时间内保持恒定，声源与接收点之间的水平距离r随时间t变化，时延差τ13(t)也随时间变化。接收信号的时频谱可近似表示为

1.2 频率干涉周期

由式(3)可知，在t时刻，接收信号时频谱沿频率轴的干涉周期为∆f=1/τ13(t)。文献[13]推导了到达时延差τ13的近似表达式

其中，c0为声源处的声速，n(z)为深度z处的折射率，α3为BSR 声线的出射角。例如，在等声速近似条件下，α3(t)=arctan{(2H+zr)/r(t)}，其中H为海深。可以看出α3随水平距离r的增大而单调递减，因此在接收深度zr恒定的前提下，τ13随r的增大而单调递减，频率干涉周期∆f随r的增大而单调递增。

图2 为声影区内频率干涉周期∆f的值随水平距离的变化曲线。由于∆f随水平距离单调变化，该特征量可用于声源距离估计。

图2 频率干涉周期随水平距离的变化曲线Fig.2 The frequency interference period as a function of the horizontal range

1.3 时间干涉周期

由式(3)可知，对于频率f，接收信号时频谱沿时间轴的干涉周期∆t可表示为

假设在时间间隔∆t内，声源运动的径向速度近似恒定为vr，BR 声线和BSR 声线的到达俯仰角分别近似恒定为θ1(t),θ3(t)，则有：

其中，cr为接收点处的海水声速。

将式(7)代入式(6)，得到频率f处的时间干涉周期∆t的表达式

图3 为200 Hz 频点处∆t的值随水平距离的变化曲线，其中vr=10 m/s。尽管式(8)中的cosθ1(t)-cosθ3(t)项导致∆t与水平距离呈非单调关系，但在距离已知的条件下可计算cosθ1(t)-cosθ3(t)的值，从而估计声源的径向速度vr。

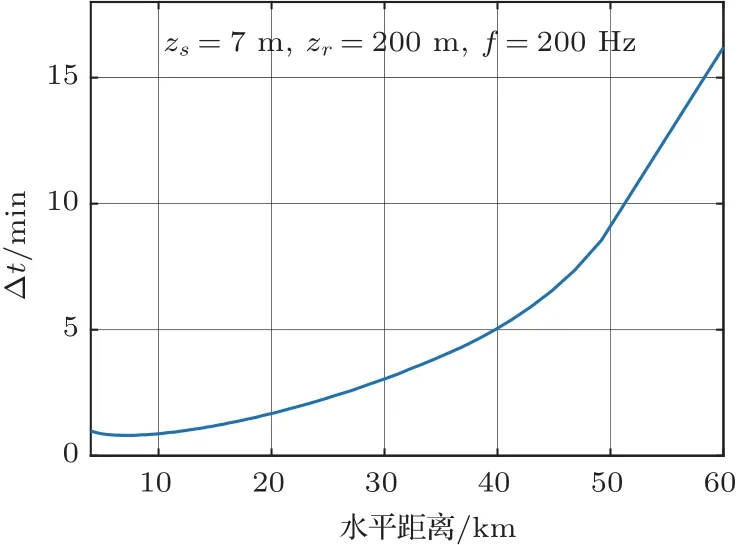
图3 时间干涉周期随水平距离的变化曲线Fig.3 The time interference period as a function of the horizontal range

1.4 时频谱的2-D FT

取一段时频谱窗Iwin(f,t)，中心时刻为t0，时长为T，中心频率为f0，带宽为B。如图4(a)所示，当选取的时长和带宽较小时，窗内的频率干涉周期∆f和时间干涉周期∆t近似恒定。经去直流处理后，该时频谱窗的2-D FT幅度谱为

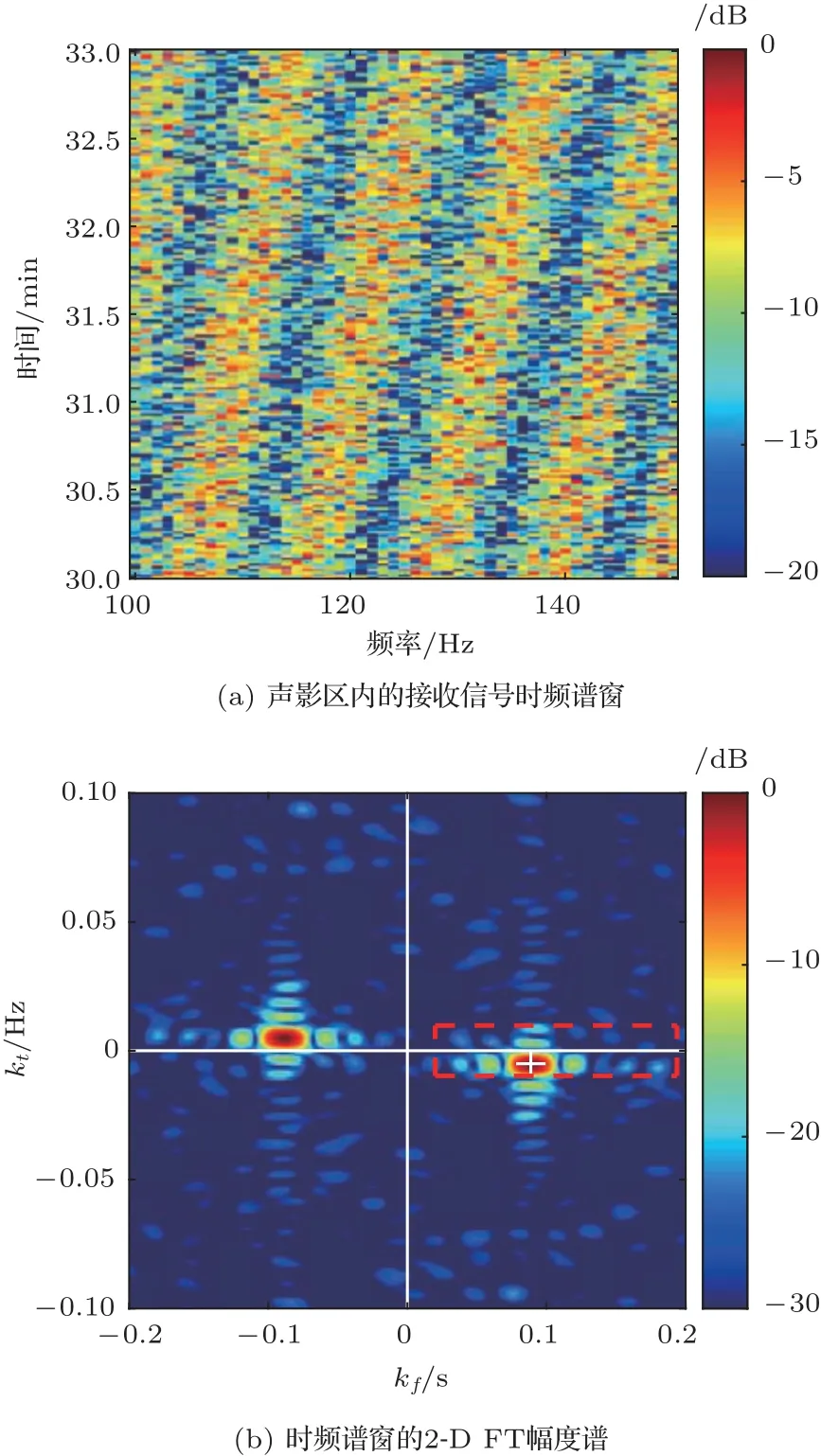
图4 时频谱及其2-D FT 示意图Fig.4 The spectrogram and its 2-D FT illustration

其中，∗表示卷积，sinc(·)表示sinc 函数，δ(·)表示Dirac 函数式(9)中，横坐标kf的单位为秒(s)，纵坐标kt的单位为赫兹(Hz)。

由于式(9)关于原点对称，以下仅讨论kf>0对应的I˜win(kf,kt)第I、第IV象限。式(9)表明，时频谱窗的2-D FT 幅度谱中，在位置将出现幅度最大值，如图4(b)中白色十字标记位置所示。

2 声源距离和径向速度估计

由第1 节分析可知，水面声源在声影区激发的声场干涉结构与水平距离和径向速度有关。对一段较小的接收信号时频谱窗进行2-D FT，可将变换前能量分散的干涉条纹聚焦在变换后能量集中的较小区域内。检测2-D FT 幅度谱中最大值点对应的横纵坐标，即可提取频率干涉周期∆f和时间干涉周期∆t，从而解算声源距离和径向速度。上述分析的前提条件是时频谱窗的处理时长和带宽较小，窗内的干涉条纹近似为相互平行的直线，而对于较大带宽的接收信号，可进行多频带处理，处理方法如下。

考虑一段接收信号，中心时刻为t0，时长为T。将接收信号时频谱分割为Q个具有一定重叠率的子频带，其带宽均为B，中心频率分别为f(1),f(2),···,f(Q)。对上述Q个子频带分别进行2-D FT 处理，相应的幅度谱最大值点横坐标记为，纵坐标记为

由式(4)可知，上述Q个横坐标相等，且与声源距离有关：

由式(8)可知，上述Q个纵坐标与对应子频带的中心频率成正比，且与声源距离和径向速度有关：

然后，对上述Q个子频带的2-D FT 幅度谱沿纵轴(kt方向)进行线性缩放并累加，得到多频带处理的2-D FT幅度谱：

式(12)中，横坐标kf的单位为秒(s)，纵坐标kt/fcenter无量纲。

本文将横坐标的界限设定为

其中，τ13,min、τ13,max分别表示τ13的最小值和最大值，由射线模型计算得到；引入±1/B项的作用是包含sinc函数沿横轴的主瓣宽度。

本文将纵坐标的界限设定为

其中，vr,max为目标船的最大径向速度，(cosθ1-cosθ3)max由射线模型得到；引入±1/T项的作用是包含sinc函数沿纵轴的主瓣宽度。

最后，通过Bellhop 射线追踪模型计算不同声源距离下τ13(r)和cosθ1(r)-cosθ3(r)的拷贝值。根据式(10)，将实际提取的与拷贝值τ13(r)进行匹配，估计声源的水平距离r(t0)；再根据式(11)，计算声源的径向速度vr。

3 数值仿真

本节通过数值仿真，验证所提出方法在低SNR条件下的有效性。

仿真环境中的海水声速剖面如图1(a)所示，海底密度为1.8 g/cm3，海底声速为1600 m/s。声源深度为7 m，以10 m/s的径向速度从水平距离3.6 km处逐渐远离至54 km 处，运动范围基本覆盖了第一影区的全部距离。接收深度为150 m，观测频带为50∼500 Hz，接收信号混有加性高斯白噪声。下面分别在接收SNR 0 dB 和-15 dB 条件下进行数值仿真。

图5(a)和图5(b)分别为接收SNR 0 dB 和-15 dB 条件下的时频谱，在-15 dB 条件下难以直接观察到干涉条纹，而在0 dB 条件下仿真结果呈现出比较明显的两种干涉条纹。其中，频率周期较大的条纹与式(2)中的τ12项有关，对于后续2-D FT 处理所选用的时频谱窗理论上可忽略，在现有的水面船辐射噪声数据中通常也观察不到此类条纹[14-16]。频率周期较小的条纹与式(2)中的τ13项有关，可用作声源距离和径向速度估计。

图5 仿真数据接收信号时频谱Fig.5 The spectrograms of the received signals from the simulations

利用所提出的2-D FT 方法分别对上述两种SNR条件的时频谱进行干涉结构检测。时频谱窗的带宽为100 Hz，频带重叠率为95%，时长为3 min，时间重叠率为90%。

图6 仿真数据中在最大值点沿自变量kf 和kt/fcenter 切片的时间历程Fig.6 The time records of slices along the independent variables kf and kt/fcenter centered on the maximum points of from the simulations

图7 仿真数据中水平距离和径向速度估计结果Fig.7 The estimated results of the horizontal range and the radial velocity from the simulations

在接收SNR -15 dB 条件下，尽管难以直接观察到时频谱干涉条纹，但利用所提出的2-D FT 方法可有效提取所需的干涉结构。沿kf方向切片的时间历程如图6(b)所示，对应的声源距离估计结果如图7(b)所示，测距结果出现了少量野点，但在大部分时间正确估计了声源距离。沿kt/fcenter方向切片的时间历程如图6(d)所示，对应的径向速度估计结果如图7(d)所示，除少量野点外，径向速度估计结果在前80 min 内的误差小于3 m/s，在第80 min后偏离真实距离。

在低SNR 的仿真实验中，所提方法的检测增益一方面来自2-D FT对干涉条纹能量的聚焦作用，另一方面来自较大的频带重叠率。假设背景噪声在整个处理频带内服从高斯白噪声分布，那么对于每个子频带，2-D FT 前后的背景噪声也均满足高斯白噪声特性。理论上，频带重叠率越高，子频带数目N就越多，公式(12)中的求和项也越多，在一定SNR 条件下可有效积累这些求和项的谱峰能量，从而提高检测增益。但事实上，由于仿真中的重叠频带取自于同一个样本源，这些重叠频带内的背景噪声不具有独立性。因此，增大频带重叠率不一定能有效增加独立观测次数，对检测增益的影响比较有限。

下面通过蒙特卡洛仿真实验，进一步分析接收SNR 和频带重叠率对测距性能的影响。仿真环境、收发深度、径向速度、时频谱窗的带宽和频带重叠率均与以上实验保持一致，声源从水平距离9.1 km 处远离至10.9 km 处(水平距离近似固定为r0=10 km、时长为3 min)，进行100 次蒙特卡洛仿真，然后统计测距结果的均方根误差(Root mean squared error,RMSE)。RMSE定义为

对于-14∼-10 dB 的接收SNR 范围，不同频带重叠率条件下RMSE 随接收SNR 变化的关系曲线如图8(a)所示。首先，在相同的接收SNR 条件下，频带重叠率越高，测距结果的RMSE越低，不同频带重叠率对应的3条曲线在-14 dB处趋于接近。其次，对于相同的频带重叠率，测距结果的RMSE与SNR 呈负相关，且RMSE 均小于0.3 km，单次测量结果即可有效实现测距。对于-16∼-10 dB 的接收SNR范围，图8(a)扩展为图8(b)。当SNR小于-14 dB 时，随着SNR 继续降低，不同频带重叠率对应的测距结果RMSE 同步显著增大，的单次估计结果不再能稳健地实现声源测距。但本节在-15 dB 仿真条件下，仍可通过的时间历程(图6(b)所示)或测距结果的点迹(图7(b)所示)观察出声源距离的变化轨迹。上述结果表明，增大频带重叠率能带来一定的处理增益，但对测距精度的影响比较有限，影响测距精度的主要因素是SNR。

图8 不同频带重叠率条件下RMSE 随接收SNR变化的关系曲线Fig.8 The relationship between the RMSE and the received SNR at difference overlapping ratios of the frequency band

以上分析中，重叠频带内的背景噪声不具有独立性。如果通过其他方法增加独立观测次数或增大等效带宽，则有机会进一步提高检测增益。此外，以上结论要求处理频带内的背景噪声满足高斯白噪声特性。对于实际的海试接收信号时频谱，背景噪声具有一定的空间分布特性，使得检测增益和测距性能通常低于仿真结果。

4 海试数据处理与分析

2022 年4 月，在菲律宾海开展了一次深海声学实验。实验站点的海深约4800 m，根据World Ocean Atlas(WOA)数据库的历史温度[20]、盐度[21]数据计算得到的海水声速剖面如图9所示。

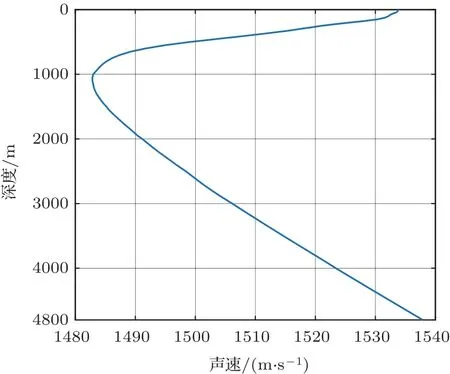
图9 实验期间的海水声速剖面Fig.9 The sound speed profile during the experiment

实验期间，一艘非合作的水面船逐渐靠近接收点而后驶离，在接收点利用近水面深度布放的水听器对其辐射噪声进行观测。其中，较高SNR 的接收信号时频谱如图10(a)所示，较低SNR 的接收信号时频谱如图10(b)所示。由于目标船的径向速度发生了多次改变，时频谱中的干涉条纹出现了多个拐点。此外，时频谱中不同区域的干涉条纹清晰程度不同，背景噪声不能简单假定为加性高斯白噪声。

图10 海试数据接收信号时频谱Fig.10 The spectrograms of the received signals from the experimental data

在图10(a)中，分别取两段时频谱窗，如图11(a)和图11(b)所示，对应的2-D FT 幅度谱分别如图11(c)和图11(d)所示。其中，图11(a)中的背景噪声更加接近高斯白噪声，因此图11(c)中的噪声分布也比较均匀，由干涉结构形成的幅度谱最大值出现在红色虚线框(第2节提出的横纵坐标上下界)之内，绝大部分噪声则分布在红框之外。与之相比，图11(b)中的背景噪声和条纹能量具有一定的空间分布特性，0.625∼0.75 归一化频带内的条纹能量明显高于0.5∼0.625 频带，导致图11(d)在坐标原点附近形成了幅度较大的伪峰，其幅度大于红框内由干涉结构形成的谱峰。因此，直接搜索2-D FT幅度谱的最大值点可能会错误地提取所需干涉周期。所幸的是，通过第2 节提出的横纵坐标上下界，类似于对时频谱窗进行二维图像带通滤波，利用横坐标下界可滤除图11(d)中的伪峰。

图11 图10(a)中两段时频谱窗和2-D FT 幅度谱Fig.11 Two segments of the spectrogram in Fig.10(a) and their 2-D FT magnitude spectrums

事实上，由背景噪声形成的谱峰有可能出现在分析的上下界内，但仍可通过谱峰的相对位置以及多频带处理后的谱峰能量加以判别。首先，受背景噪声和条纹能量分布的影响，观测到的条纹数量相比于原有数量通常减少而不是增加，因此2-D FT幅度谱中的伪峰通常比干涉结构形成的谱峰更加靠近原点。其次，式(12)将各个频带内的2-D FT幅度谱进行累加，不同频带形成的伪峰通常会出现在不同位置，因此伪峰能量在累加过程中逐渐被平均掉。综上所述，当2-D FT幅度谱中出现两个或以上谱峰时，可初步判定靠近原点的为伪峰，在多频带累加后的2-DFT 幅度谱中，可进一步判定能量较低的为伪峰。以上分析针对目标船辐射噪声的连续谱成分，当存在强线谱成分时，2-D FT 幅度谱中可能会出现其他性质的谱峰，有待进一步研究。

利用所提出的2-D FT方法分别检测图10中两张时频谱中的干涉结构，时频谱窗所用的带宽、时长和重叠率参数均与仿真实验相同。

图12 海试数据中在最大值点沿自变量kf 和kt/fcenter 切片的时间历程Fig.12 The time records of slices along the independent variables kf and kt/fcenter centered on the maximum points of from the experimental data

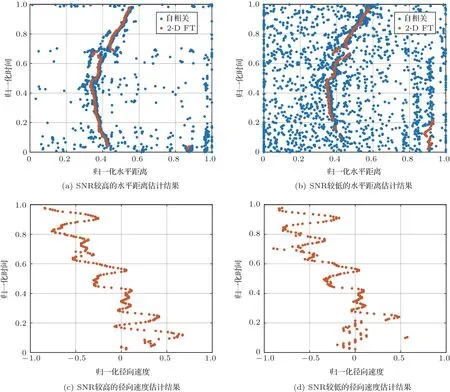
图13 海试数据的水平距离和径向速度估计结果Fig.13 The estimated results of the horizontal range and the radial velocity from the experimental data

其次，为了对比所提出的2-D FT 方法在低SNR 下的优越性，利用单个时刻的接收信号自相关方法提取∆f，得到的测距结果如图13(a)和图13(b)中的蓝色点迹所示。在较高SNR 条件下，自相关方法的测距结果能够体现距离变化的总体趋势，但野点较多，实际中需要后处理方法以消除野点。相比之下，2-D FT 方法的野点较少，测距结果的稳健性较高。在较低SNR条件下，自相关方法的测距野点过多，难以有效提取声源距离，而2-D FT方法仍然在大部分时间段实现了测距。

5 结论

利用射线声学理论，分析了深海声影区中接收信号时频谱的干涉结构，给出了频率干涉周期与声源距离的近似表达式，以及时间干涉周期与径向速度的近似表达式。利用水面船辐射噪声信号的时频谱2-D FT 幅度谱，提高时频干涉周期的检测增益，实现了低SNR 条件下声源距离和径向速度的联合估计。最后通过数值仿真和海试数据处理，验证了所提方法的有效性。结果表明，在低SNR 条件下，所提方法相比于自相关方法具有较好的稳健性。下一步工作包括研究水面船辐射噪声中的强线谱成分所形成的干涉结构。

致谢感谢参与海上实验的全体人员，他们为研究工作提供了宝贵的实验数据。感谢中国科学院声学研究所的任岁玲副研究员为实验数据处理提供了重要帮助。