基于先验驱动深度神经网络的泊松去噪变分模型

李倩，魏伟波，杨光宇，宋金涛，孙璐，潘振宽

（青岛大学计算机科学技术学院，山东 青岛 266071）

0 引言

在天文学影像［1］、生物医学影像［2］、夜视影像［3］等弱光成像系统应用中，光感受器只能接收到少量光子，所获取的图像存在散粒噪声，即泊松噪声。该类噪声与光强相关［4］，导致泊松噪声的去除难度比传统高斯噪声的去除难度更大，成为图像恢复研究中的一类重要问题。

经典的泊松噪声去除方法有Anscombe 变换［5］、Fisz 变换［6］等方差稳定变换（VST）方法。该类方法将泊松噪声转换为具有稳定方差的近似高斯噪声，再使用去除加性高斯噪声的去噪器去除噪声，最后通过逆变换得到去噪图像。MÄKITALO 等［7］提出VST 与三维块匹配算法（BM3D）相结合的去噪算法（VST+BM3D），通过对高斯去噪器去噪后的图像引用精确无偏逆，以降低应用非线性逆变换过程中产生的偏差和计算复杂度，从而提高去噪性能。AZZARI 等［8］提出基 于VST 的迭代 泊松去噪与BM3D 相结合的算法（I+VST+BM3D），将泊松观测图像与前一次迭代生成的去噪图像组成尺度泊松数据，并使用精确的无偏逆得到去噪图像的估计值，在图像恢复质量、效率方面有很大提高，是目前去除泊松噪声最先进的方法之一。然而，通过方差稳定变换得到的近似图像是不准确的，尤其在信噪比较低时，逆变换的偏差较明显。泊松噪声去除的另一类经典方法为依据泊松噪声统计量的直接方法［9-10］，如SALMON 等［10］提出依赖于高斯混合模型（GMM）的非线性主成分分析（NLPCA）和非线性稀疏主成分分析（NLSPCA）方法，可较好处理较低峰值的泊松噪声去除问题，但整体图像恢复质量较差，计算效率较低。由贝叶斯公式导出的变分模型（Le）［11］包含基于泊松噪声统计量的数据项和图像特征保持的规则项，经典的总变差（TV）规则项在去除泊松噪声的同时可以保持图像边缘，但存在阶梯效应和对比度下降问题。LÜ 等［12］和张峥嵘等［13］分别用广义总变差（TGV）规则项、欧拉弹性规则项替换Le 模型中的TV 规则项，有效克服了阶梯效应问题，但须引入更多手工调节的惩罚参数。CHOWDHURY 等［14］引入分数阶总变差（FOTV）规则项以保持复杂图像的分段平滑性，但计算复杂度高，且在低信噪比时效果不显著。

基于深度学习策略的卷积神经网络的泊松噪声去除方法［15-18］使高斯噪声去除的效率和质量得到极大提高。REMEZ 等［19］将全卷积残差神经网络应用于泊松噪声去除，但网络结构复杂且可解释性差，而基于深度学习的神经网络［20-23］是有效的解决方案。WANG 等［23］在乘性噪声去除变分模型的分裂Bregman 迭代算法中嵌入高效的高斯深度卷积神经网络（DCNN）去噪器。FENG 等［24］提出在变分模型的半二次分裂（HQS）迭代算法基础上嵌入高斯去噪器的泊松去噪反应扩散模型（TRDPD）［15］，该方法大幅提高了图像恢复的计算效率，但这种即插即用（PnP）技术仍需手动精细调参，且在低信噪比时去噪效果不显著，其主要原因是估计图像包含的噪声并不严格服从高斯分布，而是包含大量伪影信息。

本文在泊松噪声去除变分模型的迭代算法基础上，设计基于泊松噪声训练数据的端到端深度学习神经网络，以避免惩罚参数的手工调节，并提高该类噪声的去除效果。采用交替方向乘子法（ADMM）［25］设计变分模型的迭代求解算法，将原优化问题分解为多个子优化问题，并将与高斯去噪相关的子问题嵌入DPDNN 高斯去噪子网络［26］，连同其他可迭代求解的子系统构成联合训练的端到端神经网络系统。

1 泊松去噪变分模型及其ADMM 算法

1.1 泊松去噪变分模型

泊松噪声图像f的概率密度函数如下：

其中：μ为均值。据贝叶斯定理，噪声图像f恢复出理想图像u的最大后验分布如下：

其中：P(u|f)为后验概率；P(f|u)为似然函数；P(u)为先验概率。由于P(f)是已知泊松噪声图像f的概率密度函数，因此为常量。根据最大后验估计理论，u可通过最大化式（2）得到，并可通过其负对数的最小化实现。

其中：Φ(u)依据图像的Gibbs 先验分布设计。

通过以上公式可得到经典的泊松噪声去除变分模型：

其中：能量泛函中的第1 项为数据项，又称数据保真度项；第2 项为规则项，用于刻画恢复图像特征保持特性；λ为惩罚参数，用于调节图像特征保持的程度。

1.2 泊松去噪变分模型的ADMM 算法

式（4）可采用标准的变分方法及梯度下降方法求解，但其数据项由于包含对数运算容易导致数值计算困难，引入辅助变量w=logau，得到：

将式（4）转化为受式（5）约束的两变量极值问题：

式（6）的求解可借助ADMM 算法。为此，引入拉格朗日乘子σ和惩罚参数μ，构造以下增广拉格朗日泛函：

在交替优化过程中，拉格朗日乘子采用如下修正迭代：

为了分离数据项和规则项，还引入另一个辅助变量z=u，并引入惩罚参数θ建立如式（6）所示的半二次分裂形式：

依据ADMM 算法，在交替优化的每一步中交替优化单个变量，相应的子优化问题依次如下：

1.3 子优化问题求解

采用变分法，子优化问题式（11）的解w满足欧拉-拉格朗日方程：

对式（15）采用梯度下降法，并对时间变量采用显式欧拉法离散，wk的迭代计算公式如下：

同样采用变分方法，关于u的极值问题式（14）的解满足欧拉-拉格朗日方程：

最终，σk+1由式（9）计算更新。

2 基于深度神经网络的泊松去噪变分模型

2.1 DCNN 网络结构

子优化问题式（18）是经典的高斯去噪模型，采用高斯去噪网络DPDNN 的先验高斯去噪子网络DCNN［26］。DPDNN 先验高斯去噪子网络采用紧凑的改进U-Net 网络结构，在加性噪声图像恢复方面性能优越，将该子网络应用于泊松噪声去除网络设计，亦可看作其拓展应用的新尝试。DCNN 网络结构如图1 所示（彩色效果见《计算机工程》官网HTML版，下同），由特征提取和图像重建两部分组成。特征提取部分由4 个特征编码块组成，每个特征编码块由3 个卷积层3×3×64、ReLU 激活函数和1 个下采样组成，生成64 通道的特征图并将特征图的减小为输入的1/2。图像重建部分由上采样和4 个特征解码块组成。先通过反卷积进行上采样，再将编码阶段生成的相同空间分辨率的特征图进行融合生成1 个新的上采样特征图，降低了编码阶段下采样过程中的信息损失。每个解码块包括1 个1×1×64 的卷积层和ReLU 激活函数，用于将特征图的数量从128 降至64，同时还包括4 个3×3×64 的卷积层和ReLU 激活函数。在网络的最后从输入端到输出端进行跳跃连接的残差学习，提高了网络性能。

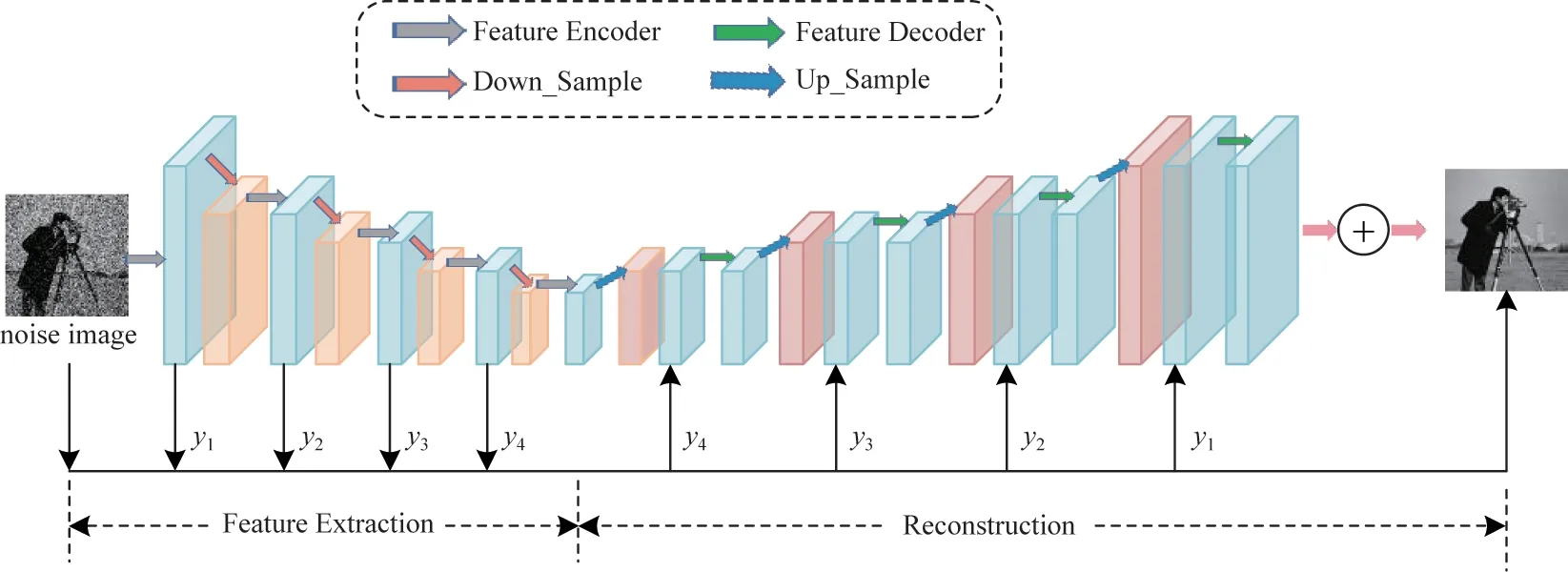
图1 DCNN 网络结构Fig.1 Structure of the DCNN network

2.2 DCNN 去噪网络结构

图2 为DCNN 去噪网络结构。通过网络执行算法的K次迭代，网络的输入是泊松噪声图像f，f初始化为u0，然后将u0输入模块，通过式（20）得到更新后的uk。高斯去噪子网络采用DCNN网络。

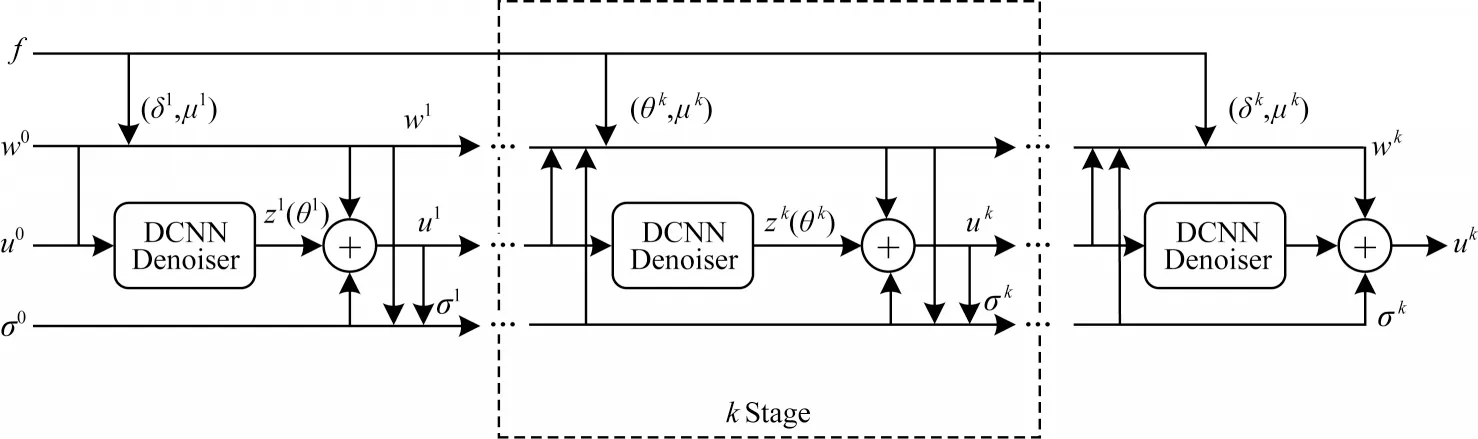
图2 DCNN 去噪网络结构Fig.2 Structure of the DCNN denoising network

通过端到端训练分别学习相关参数，所使用的损失函数为均方误差，其形式如下：

3 实验结果与分析

3.1 评价指标

以峰值信噪比（PSNR）和结构相似性（SSIM）作为定量指标，以视觉效果作为定性指标，从这两个方面对所提泊松去噪变分模型进行综合评价，PSNR、SSIM 分别定义如下：

其中：f是噪声图像；u是原始图像；μf、μu为图像f、u的均值；σf、σu为方差；σfu为协方差。

3.2 数据集与超参数

模型训练与测试均在NVIDIA GeForce TEX 2080 Ti 版本的GPU 上进行。为了训练网络，采用BSD400 数据集［26］的400 张180×180 像素的图像作为灰度图 像训练 集，采 用BSD500 数据集［27］中除去BSD400 数据集和BSD68 数据集［19］所剩下的32 张图像作为验证集。训练时数据尺寸裁剪为32×32 像素。在图片中分别添加噪声水平为1、2、4、8、20 5 种不同峰值的泊松噪声，批次大小设为20，并对不同的噪声水平进行训练。使用Adam 优化器对所提模型进行训练，优化器的超参数β1、β2分别设置为0.9 和0.99，其余参数设置为默认值。初始学习率为0.000 5，共训练50 个epochs。

迭代次数K的选择对于去噪结果的影响至关重要，因此测试不同迭代次数K的去噪效果。在峰值为2 的情况下选择K为2、3、4、5、6、7、8 的7 个网络模型分别进行训练，在Set12 数据集［19］上展示PSNR 和SSIM 的对比结果，如图3 所示。

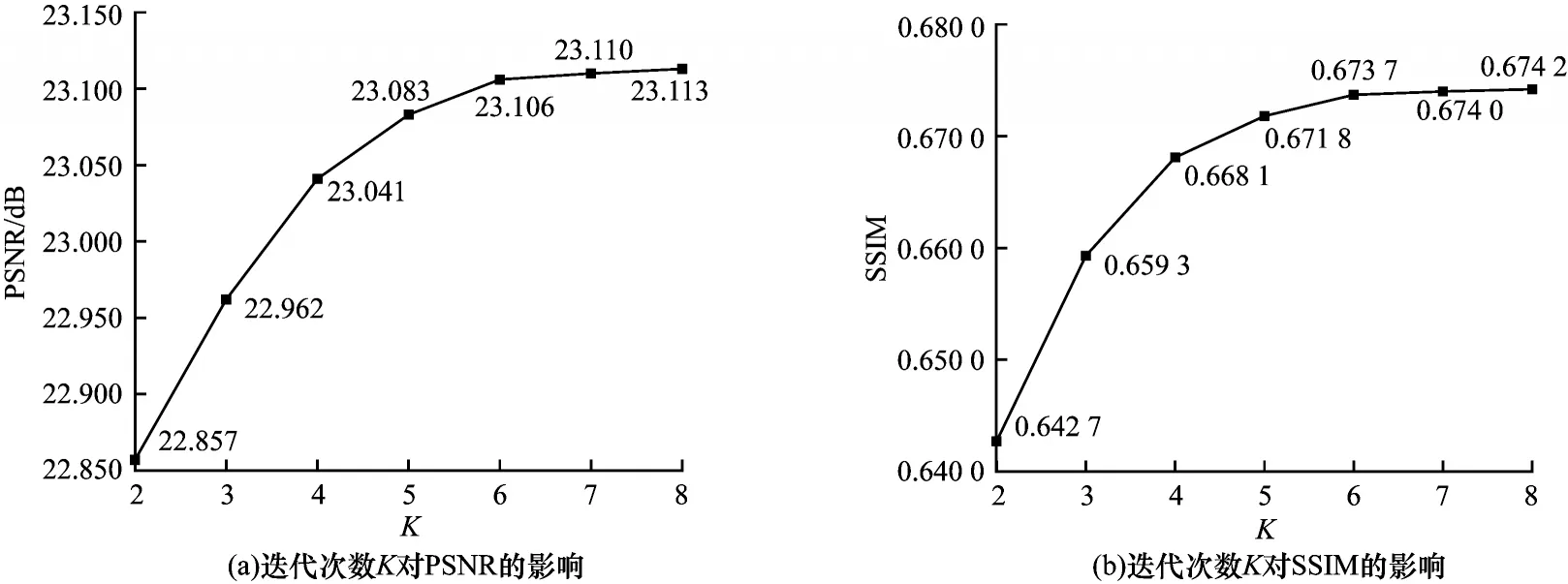
图3 迭代次数K 对泊松去噪的影响Fig.3 Influence of the number of iterations K on Poisson denoising

由图3 可以看出：当迭代次数K取6 时，相对于K取2、3、4、5 的PSNR/SSIM 可获得0.249 dB/0.031 0、0.144 dB/0.014 4、0.065 dB/0.005 6、0.023 dB/0.001 9 的增益；相对于K取7、8 时去噪效果提升不明显。通过综合考虑运行效率与去噪效果，将迭代次数设置为6 可获得良好的去噪效果。对于参数μ、θ的选择，采用固定一个值而调节另一个值的方法进行实验，当μ、θ分别取0.05 和0.95 时可以 获得较 好的去噪效果。

3.3 结果分析

3.3.1 灰度图像泊松去噪

为了验证所提泊松去噪变分模型（简称为Proposed）性能，将其与经典的基于NLPCA［10］、VST+BM3D［7］、I+VST+BM3D［8］以及深度学习TRDPD［24］的泊松去噪模型在Set12 数据集和BSD68 数据集上进行比较。

在实验中，通过在Set12 数据集上添加峰值分别为1、2、4、8、20 的泊松噪声来生成噪声图像。图4～图8 展示了部分图像的去噪效果。图4 展示的是峰值为1 时5 种模型去除泊松噪声后的效果，可以看出：经过NLPCA 去噪后会产生明显的条状伪影且图像细节过于模糊，只能恢复出图像轮廓；基于BM3D 的VST+BM3D 和I+VST+BM3D 模型在去噪后出现了散斑，这是由于BM3D 去除噪声的原理是通过选择相似块在变换域进行滤波得到块评估值，当噪声很大时会受到相似块的影响形成散斑；经过TRDPD 处理后的图片细节保留较好，但会产生块状伪影；所提模型具有较好的主观视觉效果，在PSNR 和SSIM 指数上也得到了最好的结果，但在细节保持上略差于VST+BM3D、I+VST+BM3D 和TRDPD，弱化了部分关键结构，例如，在图4（f）中房间细节处理过于平滑，而其他3 种模型可以看到更多房间的细节。由图5～图8 可以看出：无论峰值大小，经过NLPCA 的处理都会产生不同程度的条状伪影；当峰值等于2 时，VST+BM3D 和I+VST+BM3D 两种模型会产生明显的散斑，当峰值大于2 时这两种模型在视觉效果方面都有较大的改善，TRDPD 的块状伪影也不再出现；所提模型在视觉上展现的效果最好且PSNR 和SSIM 总是最高的，不仅在高信噪比时噪声可以被去除，在低信噪比时也能很好地去除泊松噪声，并且不会出现伪影和散斑等现象。因此，所提模型在去除泊松噪声方面有显著的效果。

图4 峰值为1 时不同模型的去噪效果Fig.4 Denoising effect of different models when the peak is 1

图5 峰值为2 时不同模型的去噪效果Fig.5 Denoising effect of different models when the peak is 2

图6 峰值为4 时不同模型的去噪效果Fig.6 Denoising effect of different models when the peak is 4

图7 峰值为8 时不同模型的去噪效果Fig.7 Denoising effect of different models when the peak is 8

图8 峰值为20 时不同模型的去噪效果Fig.8 Denoising effect of different models when the peak is 20

在Set12 数据集和BSD68 数据集上采用不同去噪模型的去噪结果分别如表1 和表2 所示，其中最优结果以黑体表示，下同。由表1 可以看出：当峰值为20 时NLPCA 的PSNR 低于峰值为8 时的PSNR，说明NLPCA 的去噪性能不稳定；当峰值为1 时TRDPD的PSNR 和SSIM 均低于I+VST+BM3D，说明当噪声峰值比较低时I+VST+BM3D 的去噪性能要优于TRDPD；所提模型在5 个噪声峰值上均得到最高的PSNR 和SSIM。经验证，所提模型具有较强的泊松去噪能力。

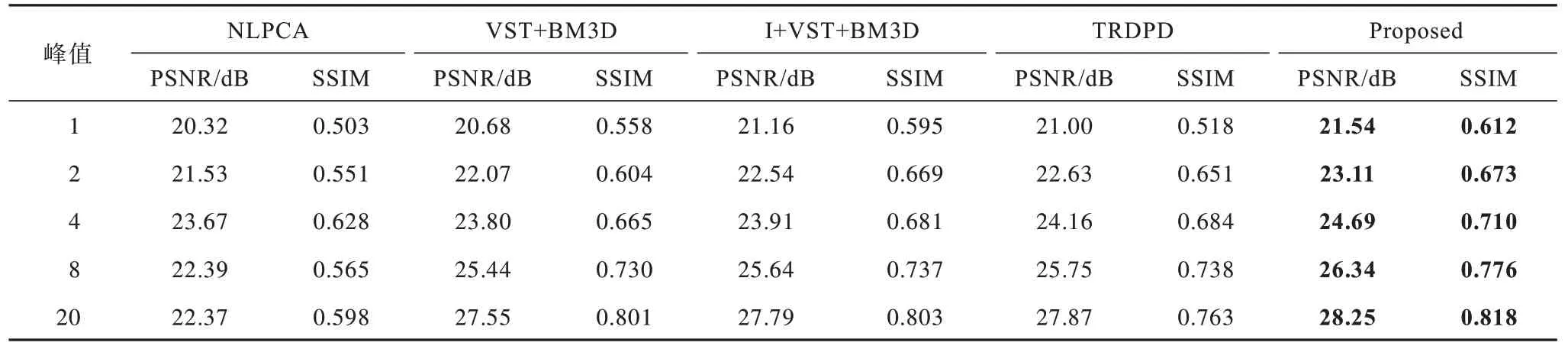
表1 不同模型在Set12 数据集上的PSNR 和SSIM 结果 Table 1 PSNR and SSIM results of different models on the Set12 dataset

表2 不同模型在BSD68 数据集上的PSNR 和SSIM 结果 Table 2 PSNR and SSIM results of different models on the BSD68 dataset

3.3.2 彩色与临床正电子发射断层扫描与计算机断层扫描（PET/CT）图像泊松去噪

为了更真实反映所提模型与其他模型在主观视觉上的效果，在CBSD68 数据集［28］上将其 与NLSPCA［10］、I+VST+BM3D 和TRDPD 进行主观视觉效果实验。图9 显示了在泊松噪声峰值为1 时的彩色图像主观视觉效果比较。由图9 可以看出：彩色图像经过NLSPCA、I+VST+BM3D 处理后会产生不同程度的模糊情况；经过TRDPD 处理后也会产生伪影；所提模型具有较好的去噪效果，特别是颜色伪影较少。

图9 峰值为1 时不同模型对彩色图像的去噪效果Fig.9 Denoising effect of different models on color images when the peak is 1

表3 为3 种模型与所提模型在CBSD68 数据集上的PSNR 和SSIM 比较，由NLSPC、I+VST+BM3D和TRDPD 处理的彩色噪声图像在数据指标上明显低于所提模型，可以看出所提模型在去除彩色图像的泊松噪声方面也具有较好的效果。

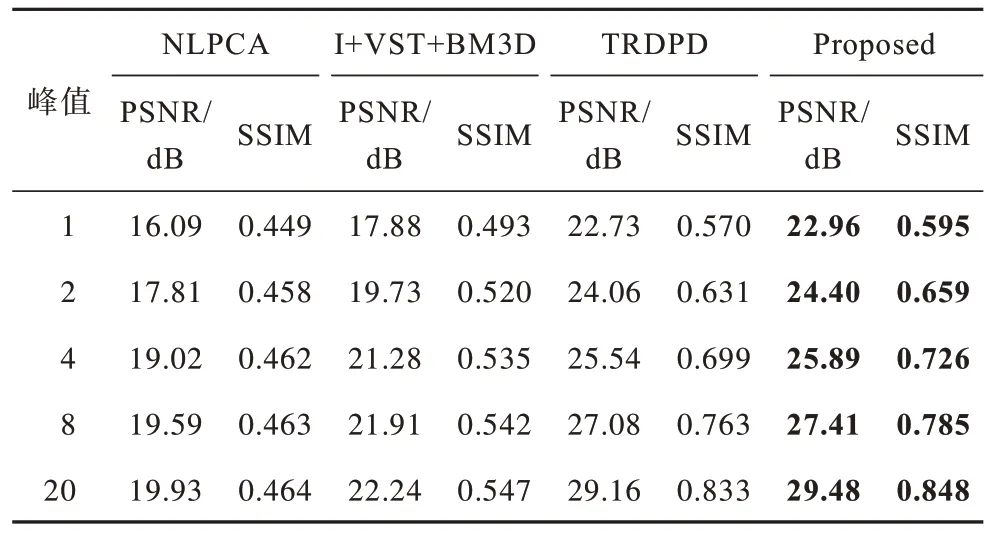
表3 不同模型在CBSD68数据集上的PSNR和SSIM 结果Table 3 PSNR and SSIM results of different models on the CBSD68 dataset

为了证明所提模型的有效性，利用两幅实际临床脑部PET/CT 图像进行实验。图10 展示的是脑部PET/CT 图像和经4 种模型去噪后的图像。由图10可以看出：临床PET/CT 图像经过NLSPCA 和I+VST+BM3D 处理后虽然去除了噪声，但图片却很模糊；经过TRDPD 处理后会产生一定程度的伪影；经过所提模型处理后的图片既去除了噪声，又避免了伪影的产生，且较好地保持了脑部结构。

图10 脑部PET/CT 图像Fig.10 Brain PET/CT image

3.3.3 运行时间比较

不同模型处理单幅图像的运行时间如表4 所示。由表4 可以看出，通过使用深度神经网络模型进行去噪的运行时间明显短于传统模型去噪的运行时间，表明深度学习方法适合在GPU 上运行，可以极大地提高运行效率。当处理256×256 像素的灰度图像时，所提模型的运行时间比TRDPD 慢0.08 s，但比NLPCA、VST+BM3D、I+VST+BM3D 分别快9.31 s、0.71 s、0.23 s；当处理512×512 像素的灰度图像时，所提模型要比TRDPD 慢0.07 s，比NLPCA、VST+BM3D、I+VST+BM3D 分别快62.51 s、3.41 s、1.50 s，说明所提模型具有较高的运行效率。

表4 不同模型处理单幅图像的运行时间Table 4 Running time of single image processed by different models 单位：s

4 结束语

本文首先设计泊松噪声去噪变分模型的ADMM 算法，将原优化问题分解为高斯去噪和图像重建两个交替优化子问题；然后根据迭代算法与深度神经网络结构的对应关系将迭代过程展开成端到端的网络求解。高斯去噪采用先验驱动的深度卷积神经网络实现，图像重建通过解析求解实现。基于标准数据集的训练和测试结果表明，在灰度图像、彩色图像及临床PET/CT 图像的泊松噪声去除方面，所提模型在客观评价指标和主观视觉效果上比传统模型和现有深度学习模型更具优势。本文工作主要是对基于深度神经网络的泊松噪声去除变分模型的初步探索，如何将其应用于去除其他噪声以及基于加速的ADMM 算法设计更加高效的变分神经网络还有待进一步研究。