一种高精度时频综合及守时方法
2024-02-28戴群雄尹继凯
戴群雄,尹继凯
( 中国电子科技集团公司第五十四研究所, 石家庄 050081 )
0 引言
在各类地面固定、车载、舰载平台建设中,时频系统为平台提供统一的时间频率基准,保证各用时单元工作在连续、一致、稳定的时间参考下[1].
传统时频系统通常采用普通恒温晶振作为频率源,通过接收卫星导航信号,获取卫导系统参考时间与本地晶振的钟差,根据钟差对晶振频率准确度进行校准,输出与参考时间同步的本地时间频率信号[2-3];当参考信号丢失时,通过晶振守时维持时间频率信号输出[4]. 由于晶振频率准确度、频率漂移等指标不高,守时精度偏低,且单个时钟源组成的守时平台,其可靠性不足. 本文提出了一种高精度时频综合及守时方法,设计了一种高精度时频综合及守时系统,首先对国内外常用的四种高稳频率源进行综合分析比较,优选高性能铷钟作为频率基准源,然后设计多钟联合时频综合处理方法,分析比较国内外主流的综合原子时算法,优选适用于本方案的加权平均算法,并在该算法的基础上,进行同类源实时互比标定设计,选择最优主钟和备钟,保证系统频率源一直处于最优状态,使系统持续稳定对外输出时频基准信号,从而提升系统的守时性能.
1 时频综合及守时系统组成框图及基本原理
时频综合及守时系统通常由导航信号接收机、频率基准、时频综合处理模块和时频标扩展模块等四部分组成[5],如图1所示.

图1 时频综合及守时系统组成框图
时频综合及守时系统是以卫星导航时间为参考,对本地时钟进行驯服及校准的系统. 其基本工作原理:导航信号接收机接收卫星导航信号,输出代表卫星系统时间的基准秒脉冲(1 pulse per second,1 PPS),时频综合处理模块测取基准1 PPS与本地频率基准的钟差信息,根据钟差信息对本地频率基准进行驾驭与驯服控制,从而获得与导航系统时间精确同步的时频基准信号. 卫星信号有效时,系统通过频率基准跟踪同步卫星系统时间,能够保证系统时间同步性能;当卫星信号丢失时,通过频率基准数据、历史调钟数据等信息的综合计算得到驯服参数,对频率基准进行驾驭,保证设备的守时性能和时频基准连续、稳定的输出.
时频综合处理模块的时钟处理精度以及本地频率基准的精度都是影响系统守时精度的关键因素. 本文重点从时频综合处理方案的优化以及频率基准精度的优化来提升系统守时性能.
2 系统时频综合及守时性能优化方案
2.1 频率基准源优选
本文研究内容侧重于通用化、小型化、低成本的设计原则,解决适用范围更宽泛,使用场景更简单的高精度守时应用需求. 现代市面常有的频率基准源通常包括恒温晶振、铷原子钟、铯原子钟、氢原子钟[6],这些基准的精度、体积、价格等因素均会制约小型化、通用化、低成本、高精度的守时应用需求,需进行综合比较,选择最优方案.
1)铯原子钟
铯原子钟是一种精密的计时器具,利用铯原子在微波激励信号感应下发生能级跃迁时辐射出来的电磁波作为标准,去调整校正振荡器,将其输出频率锁定到铯原子的跃迁频率. 铯钟的频率漂移小,目前,最好的铯原子钟达到500万年才相差1 s,多应用于科研机构或专门的计时测量机构,如国际原子时比对机构等[7]. 由于铯钟造价较为昂贵,对于大众通用型时频系统的设计,无论从价格、体积和功耗考虑,均不能满足要求.
2)氢原子钟
氢原子钟与铯原子钟一样,同样作为一种精密的计时器具,原理与铯钟基本一致,是利用氢原子能级跃迁时辐射出来的电磁波去控制校准振荡器,使振荡器输出频率与原子跃迁频率具有相同量级的准确度,进而控制钟的走动. 氢钟的漂移特性与铯钟接近,每天变化约为十亿分之一秒,达到300万年相差1 s,其短期稳定性比铯钟稍强,被广泛用于导航定位、时间计量、航天测控、射电天文观测、守时服务、火箭和导弹的发射等方面. 氢钟的造价比铯钟更加昂贵,且体积普遍比铯钟更大一些,因此也不能满足要求.
3)恒温晶振
恒温晶振是目前应用较为广泛的一种频率发生装置,由振荡电路、直流稳压电路和恒温槽控制电路构成,工作原理就是通过接收外部同步参考信号,对自身振动频率进行校准,使之与参考信号的频率精度接近,再通过恒温槽控制电路对晶振的晶体谐振器的供电电流进行控制,使得谐振器保持一种恒定的温度;当处于无外部参考后的特定时间段内时,可以守时维持相应精度的时间输出,守时能力能达到优于10 μs/d,目前恒温晶振已经成为时频系统中最常用的一种时间源保持时钟. 其特点是体积小、功耗低、具有一定的守时能力,可以作为频率基准源的选择方案之一.
4)铷原子钟
铷原子钟是目前时频系统中应用广泛的一种高配置的时钟源,其原理与铯钟、氢钟基本一致,是利用铷原子在激励下发生能级跳跃时辐射出来的电磁波去校准振荡器的频率准确度[8]. 铷钟通常相比铯钟和氢钟其漂移特性和稳定性稍差些,很少应用于专门的计时测量机构和高精度时间计量及比对任务,但其体积、功耗和造价远低于前面两种原子钟,且性能稳定,质量可靠,为目前技术成熟且最为常规的一种原子频标,其中短期稳定度和准确度较好[9]. 对于高需求的时频服务行业是一种必选的配置. 通过接收卫星信号,铷原子钟在很短时间内(约30 min)将卫星的频率信号稳定住、保持住,在无卫星信号输出的状态下,其保持时间的精度可达到优于1 μs/d,守时能力强,因此,配置铷原子钟是也是合适方案之一.
经过分析比较,铯原子钟和氢原子钟性能优越,大多应用于科研机构或专门的计时测量机构,但受限于其体积大、价格高、功耗大等因素,对于适用面广、使用场景简单且具有高精度守时应用需求的领域显然不能作为合适方案;而恒温晶振和铷原子钟目前广泛应用于现代工业的各个领域,适用性更强,均可作为通用型、高精度时频综合及守时系统的频率基准.下面列表进行综合比较,选择最优方案.
表1中,对市面上常用的恒温晶振和铷原子钟的主要性能指标进行比较,包括频率准确度、频率稳定度、频率漂移、工作温度、温度特性、功耗、体积[10]、价格等,综合比较,晶振的功耗、体积和价格均优于铷原子钟,铷原子钟在频率准确度、频率漂移、温度特性方面优于晶振,而拥有较高的频率准确度、频率漂移指标及温度特性指标,对设备的守时性能和长期稳定性更为关键. 现在通用的时频装备通常设计成标准机架式结构,其尺寸通常为1 U (1 U=4.445 cm)及以上,该尺寸并不影响铷钟的装配,铷钟功耗和价格相比晶振稍高些,但并不成为制约装备设计的主要因素,而装备的长期稳定性、高守时性能对系统更为关键和实用. 因此,综合比较而言,铷原子钟成为优选方案.

表1 恒温晶振和铷原子钟性能比较
2.2 多钟联合时频综合处理
系统设备内置高性能铷原子钟,在卫星信号有效的前提下,通过时差测量及数据处理,获得铷钟与时间源的钟差,根据钟差数据校准铷原子钟频率,实现精密时间溯源与同步;卫星信号丢失后,铷钟从时间同步状态进入守时状态,通过历史调钟数据、铷钟数据等信息的综合计算和驾驭处理,保证设备的守时性能.
高精度时频综合及守时方法在原有单钟源设计方案的基础上,设计了多钟联合时频综合处理方案,有效利用系统的多铷钟资源,提升系统守时精度[11],同时兼顾高可靠性,为其他用时系统提供高质量时频服务. 图2所示为多钟联合时频综合处理方案原理框图.
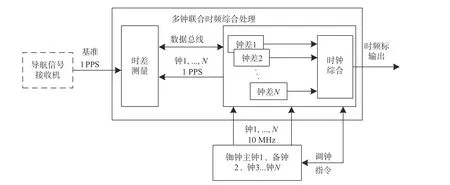
图2 多钟联合时频综合处理方案原理框图
系统配备多台铷钟,通过时差测量单元分别测取每台铷钟与参考源的钟差以及各台钟之间的钟差[12],时钟综合单元根据钟差分析出各台铷钟的质量和特性,然后根据铷钟质量和特性分配权重[13-14],实现多铷钟时钟综合,输出综合后的时钟,相比单时钟,时钟性能得到有效提升;当其中一个铷钟出现故障时,根据钟差变化特性可实现故障钟判断与快速切出,其他铷钟继续维持时钟输出,系统时钟输出稳定可靠[15].
目前国际主流的综合原子时算法主要包括加权平均算法和各种滤波类算法[16-17]. 加权平均算法的具体做法是:根据某个计算周期中钟组内各原子钟的稳定度来确定每台原子钟在此计算周期内的权重,通过合理的权重分配,使钟组内的噪声最小. 国际计量局(The International Bureau of Weights and Measures,BIPM)采用加权平均算法对参与国际原子时比对的守时实验室钟组的数据进行加权平均,以此来提高综合原子时的稳定度. 滤波类算法主要为卡尔曼滤波(Kalman filter, KF)算法,通过该算法对原子钟组噪声进行统计与建模,抑制原子钟噪声带来的影响. KF算法的稳定性较好,但是存在发散性的问题[18].
本文采用加权平均算法来实现铷钟钟组综合,各钟权重依据钟实际运行性能和比对测量精度进行自适应控制,实际计算时采用给定时间的阿仑方差作为权重计算的依据. 依据权重计算的结果,综合钟组自由运行的各原子钟数据,处理得到自由的综合原子时,再依据导航接收机输出的北斗时基准,经频率驾驭得到与北斗时同步的综合原子时,在守时期间,测量出各钟与综合时间的频差和相差,结合历史驾驭数据,根据权重调整综合时间的频率和相位,实现高精度守时. 理论上,综合原子时算法的最主要内容是根据原子钟组内的N台原子钟,利用N-1组原子钟差对各原子钟进行权重计算及调整,使其对钟组产生的综合原子时影响最小化[19],由此生成的综合原子时比钟组内任何一个原子钟具有更高的稳定性、可靠性和频率精度. 钟组产生的综合原子时是采用数学方法计算得到的,并不是某台钟的时间也不是他们简单的集合. 其算法具体如下:
若有N台原子钟,其读数为hi(t) ,i=1,2,3,···,N,利用加权平均算法,建立一个综合原子时TA(t) .
式中,wi(t)为原子钟i的权重. 由于钟组内的原子钟相互独立,且每台原子钟的性能不同,需采用原子时综合处理的方式,对每台钟进行合理加权与控制,从而获得一个比任何一台钟更稳、更准的综合原子时[20],尽可能抑制或消除原子钟噪声带来的影响.
TA(t)即是综合钟,TA(t) 的噪声是各钟噪声加权和
为了使综合钟的噪声 εA(t) 最小,通常按照式(3)计算权重
在进行综合原子时计算时,当参与原子时计算的钟数量发生改变或某台钟i的权重发生改变时,为了不影响时间的连续性,增加改正量为钟i在t时刻读数的预测值[21]. 所以式(1)可以写为[22]
式中,wi(t) 和的计算在不同原子时算法中计算方法不同.
由式(4)变换得到
为计算得到TA(t) 的数值,设钟i和TA(t) 的差为xi(t),记为
xi(t)可以从钟i和钟j的差Xij(t) 的比对数据中求出.Xij(t) 可通过测量得到
由式(5)、(6)得到
由式(7)、(8)组成方程组
式(7)共给出N-1个方程式,结合式(8),共N个方程,可以解算得到N个xi(t).xi(t) 表示为
h′i(t)可通过线性预测得到. 预测公式为
式(11)中:t0为上一次计算的最后时刻;xi(t0) 为t0时刻钟i相对于TA(t) 的时间偏差预测值;y′i(t) 为t0时刻钟i相对于TA(t) 的频率偏差预测值,一般通过最小二乘法计算得到;预测y′i(t) 所用的参考是TA(t) ,若计算TA(t)的方法不合理,则前期计算得到的TA(t) 会影响y′i(t)的准确性.
在进行多钟综合的过程中,通过计算得到的综合原子时并非实时的物理信号,而是一个纸面时间,必须选择一台原子钟作为系统主钟,通过主钟来产生实时物理信号. 本文采用铷原子钟作为物理信号频率源,由于不同类型的原子钟性能差异较大,而同种类的原子钟差异相对较小,为了减少型号差异对系统综合原子时性能带来的影响,应尽可能选用同型号的原子钟;当选择同型号原子钟时,还需选择性能最优的原子钟作为主钟. 主钟输出频率信号的短期稳定度由本身物理特性决定,无法通过算法补偿等方式来提高,即使通过具有良好长稳定特性的北斗时等参考驾驭的方式也只能改善其长期稳定度. 因此,选择主钟的依据之一是具有优秀的短期频率稳定度.
传统测量原子钟频率稳定度的方式为单次标定方式,即在组建原子钟组前,仅对每台原子钟自由运行的时差值分别进行测量,对测量得到的数据进行分析和计算,根据计算结果选取最优主钟. 随着时间推移或者其他异常因素影响,原子钟的性能可能会随之发生变化,无法保证主钟一直处于最优状态,因此,这种单次标定方式存在固有缺陷,会给综合原子时的长期稳定运行带来一定的风险. 为了弥补这种风险,本文设计实时标定的方式,即原子钟加入原子钟组后,在系统运行过程中,实时对每台原子钟的时差值进行监测,根据监测数据进行计算,获取最优性能的主钟,保证所选主钟一直处于最优状态. 本文设计的多钟联合时间频率综合与守时系统为试验验证系统,同时考虑系统通用性和低成本,设计铷钟数量为3台,按照同类源实时互比标的方式,分别测得3台钟互比的钟差 σy12(τ) 、 σy13(τ) 、 σy23(τ) ,则互比结果满足以下关系:
式中: τ 为取样时间; σy12(τ) 为铷钟1、铷钟2互比测得的阿伦标准方差; σy13(τ) 为铷钟1、铷钟3互比测得的阿伦标准方差; σy23(τ) 为铷钟2、铷钟3互比测得的阿伦标准方差.
按照式(12)、式(13)、式(14)分别算出三台钟的时域短期稳定度 σy1(τ) 、 σy2(τ) 、 σy3(τ) .
式中, σy1(τ) 、 σy2(τ) 、 σy3(τ) 分别为铷钟1、2、3的短期稳定度, τ 是取样时间.
通过同类源实时互比标定的方式对钟组短期稳定度进行计算与评估,选择最优主钟和备钟,由于方法实时性,可选择当前性能最好的钟为主钟,同时当主钟出现故障时,能切换至备钟,保证输出频率信号连续,系统不间断运行[23-24].
3 试验验证与分析
为了验证本文提出方法的有效性和可行性,首先优选高性能铷原子钟作为频率基准源,随着国产原子钟技术水平的突破,为了提升自主可控性[25],本方案选用国产铷钟,其指标如表1所示,然后设计传统单钟时频系统和多钟联合时频综合及守时系统,按照如图3所示搭建试验验证平台.
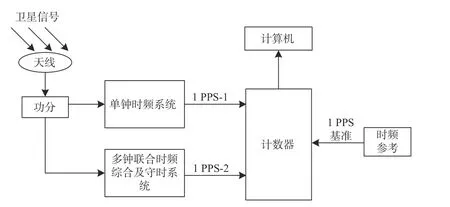
图3 试验验证测试连接图
为保证试验验证的科学性和有效性,通过功分器将天线信号一分为二,输出给单钟时频系统和多钟联合时频综合及守时系统,且进行同时段测试,以去除不同天线、不同时间段测试带来的误差影响. 时频参考采用标准型接收机或守时型铯原子频标.
时频参考的选择对测试结果很重要. 守时型铯原子频标本身会随着时间存在漂移,目前国产的高性能铯原子频标,其漂移约为40 ns/d,且不同批次、不同型号的铯钟其守时性能存在差异,因此并不适合作为高精度时频系统的测量参考;标准型接收机授时精度约为30 ns,本身误差较大,无法作为高精度时频系统的测量参考. 目前基于北斗三号(BeiDou-3 Navigation Satellite System,BDS-3)的精密单点定位(precise point positioning,PPP)技术的高精度授时型接收机,其授时精度可达2~3 ns,误差小且技术成熟稳定,可作为时频参考. 但接收机本身存在绝对零值误差,会影响测试结果. 因此,在进行正式测试前,需对高精度授时型接收机进行零值标定,标定方法为:以标准时间源为基准,通过计数器测量获取接收机输出时间与标准时间源的时间差,该时间差值即为接收机绝对零值,将零值设置进入接收机,完成零值标定处理. 零值标定原理框图如图4所示.

图4 高精度授时型接收机零值标定原理框图
高精度授时型接收机零值标定结束后,按照图3所示的试验验证测试连接框图开展测试验证. 为了减少温度变化对测试带来的影响,将测试验证平台置于温度相对稳定的环境. 具体测试步骤如下:
1)按照图3所示连接设备,将设备输出1 PPS-1、1 PPS-2以及时频参考输出1 PPS基准接入计数器,设备加电;
2)待设备锁定卫星24 h后去掉天线,使用计算机采集计数器测量的时差数据;
3)连续测量4 h后,分别获得1 PPS-1、1 PPS-2与1 PPS基准的钟差数据,记为r1、r2;
4)计算max(r1)-min(r1),max(r2)-min(r2),即获得单钟及多钟系统的守时指标.
图5所示为试验结果. 其中,图5(a)为单钟时频系统守时结果、图5(b)为多钟联合时频综合及守时系统守时结果,4 h守时精度分别为93.26 ns和39.87 ns.结合实测数据来看,经过多钟联合时频综合优化后,系统守时精度优化了53.39 ns,得到了有效提升,由此验证了本文提出的高精度时频综合及守时方法的有效性和可行性[26].

图5 试验验证守时性能实测结果
4 结束语
本文针对传统单钟源时频系统守时精度偏低、可靠性不足的问题,提出了一种高精度时频综合及守时方法,通过频率基准源优选、多钟联合时频综合处理的技术手段设计实现了高精度时频综合及守时系统,以满足高精度的守时服务应用需求,并搭建了试验验证平台,验证了该方法的可行性和有效性. 方法主要优点总结如下:
1)从性能、尺寸、价格、适用范围、可靠性等多个方面,对现代市面常有的恒温晶振、铷原子钟、铯原子钟、氢原子钟等频率源进行了综合比较和分析,优选铷原子钟作为频率基准,兼顾通用性强、性能优越的特点,满足高精度守时应用需求;
2)通过多钟联合时频综合处理,优选适用于本方案的加权平均算法,得到比任何单钟更稳定的综合原子时,并进行了同类源实时互比标定设计,选择最优主钟和备钟,保证系统频率源一直处于最优状态,从而提升系统的守时性能;同时通过该方法可实现:当主钟出现故障时,实现故障钟判断与快速切出,备钟继续维持时钟输出,系统时钟输出连续、稳定和可靠.
该方法通过设计、验证并工程化实施后得出,可有效解决传统单钟源时频系统守时精度偏低、可靠性不足的问题,实现高精度时频综合及守时系统,提供高质量时频服务,也为相关行业应用提供可借鉴的设计方案,应用前景广阔.
