基于LSTM的北斗三号卫星差分码偏差分析及预测

刘晓文

( 山东广源岩土工程勘察有限公司, 山东 烟台 264000 )

0 引言

GNSS差分码偏差(differential code bias，DCB)，是由不同类型的GNSS信号之间的差异产生的时延差异，按照硬件是设备分为卫星端差分码偏差和接收机端差分码偏差，按照频率相同或不同又分频内偏差和频间偏差[1]. DCB作为电离层建模的必须要分离的重要误差，其精度对电离层总电子含量(total electron content，TEC)具有非常大的影响，严重的可以达到30电离层TECU左右的偏差[2]，从而进一步影响到导航定位的精度. 2020年6月，北斗三号(BeiDou-3 Navigation Satellite System，BDS-3)组网成功，BDS-3在继承北斗二号(BeiDou-2 Navigation Satellite System，BDS-2)的频率基础上，增加了两个新频点B1C和B2a，且同一频点具有多个支路，由此产生的新偏差[3].目前能够连续提供稳定的北斗卫星导航系统(BeiDou Navigation Satellite System，BDS) DCB产品的机构有德国宇航中心(Deutsches Zentrum für Luft- und Raumfahrt，DLR)和中国科学院(Chinese Academy of Science，CAS)，其中DLR采用全球电离层格网模型确定电离层延迟，进而实现DCB参数的确定[4]. 作为电离层的副产品，DCB的精度会受到不同的电离层模型、等效高度、投影函数、插值拟合等因素的影响，太阳活动、地磁活动、天气环境等因素产生的电离层TEC 变化也会引起DCB的精度和稳定性[5-6]. 在解算DCB参数的时候，通常采用零基准约束进行分离卫星DCB和接收机DCB[7-9]，即所有的卫星或测站DCB为零. 当卫星数目发生改变时，需要重新调整基准，会使得所有DCB参数产生偏差[10-11].

为了解决DLR和CAS发布的DCB产品时延问题、缺失卫星差分码偏差及其导致的卫星基准变换引起的偏差问题. 本文通过采用机器学习的方法，即长短时记忆(long short-term memory，LSTM)神经网络来研究和分析BDS-3新频点长期和短期变化特性，对卫星DCB参数进行预测，以预测值代替真实值，实现了短期预报.

1 BDS-3 DCB 预测方法

1.1 DCB估值基准统一

由于在分离卫星DCB与接收机DCB时，卫星和接收机端DCB线性相关，会造成法方程秩亏[1]，因此我们通常将所有卫星DCB之和约束为0进行参数分离. 当分析一段时间内的DCB值时，可能会存在某几天的卫星DCB参数缺失或者新的卫星参与计算的情况，会导致基准发生变化，从而使得卫星DCB值产生偏差，因此需要将每一天的基准转换到统一的基准上面，只有基准统一了才能准确有效的对卫星DCB进行评价. 假设A基准有uA颗卫星，采用所有的卫星DCB和为0，其约束方程为

式中：IuA为系数阵；为A基准下的卫星端DCB参数；uA为卫星数量.

假设统一A基准和B基准，其中A采用了uA颗卫星，B采用了uB颗卫星(uB＜uA)，通常选择卫星少的一方构建新的基准，即A基准的卫星包含了B基准的卫星，需要将A基准的调整至与B相同的基准.其约束方程有

1.2 多项式拟合法

利用多项式拟合的方式，基于最小二乘法法则，生成N阶多项式函数，表达式如下

式中：n为多项式的阶数；pn(x) 为拟合出的多项式函数；x为输入的变量.

通过多项式函数对已有的数据进行拟合或者插值. 本文采用最小二乘法对各卫星频间偏差参数进行二阶多项式拟合，并将拟合出的函数对差分码偏差预测.

1.3 LSTM神经网络模型

LSTM是一种时间循环神经网络，相较于循环神经网络(recurrent neural network，RNN)，LSTM能够在长序列训练当中避免梯度消失和梯度爆炸的问题[12-13]. LSTM模型神经元结构如图1所示.

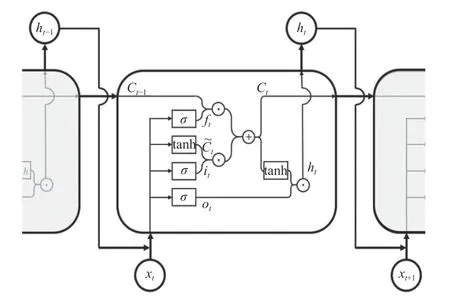
图1 LSTM神经网络的内部结构

LSTM 神经网络单元通过遗忘门、输入门和输出门来替换原有的RNN神经网络单元，而LSTM之所以能够解决RNN的长期依赖问题，是因为LSTM引入了门(gate)机制用于控制特征的流通和损失[14-16].遗忘门决定了上一时刻的细胞状态ct-1中的那些信息被遗忘，遗忘门ft公式为

在输入门中，激活函数使用了 tanh 函数来进行更新当前时刻的单元状态，再通过遗忘门留下的信息ft、上一时刻的信息Ct-1和更新后的候选值得到新的值，从而实现了当前记忆和长期记忆的结合[17]. 具体公式为

式中：it为输入门输出；wi为输入门的权重；bi为输入门的偏置项；C为候选信息；wC为候选单元的权重；bC为候选单元的偏置项；Ct为得到的新单元的信息；其余参数同式(5).

在输出门中的输出ot和t时刻单元的输出ht公式如下：

式中：wo为输出门的权重；bo为输出门的偏置项.

通过对大量样本数据的学习，反复更新LSTM内部的权阵以及参数，即可完成LSTM的训练，从而实现对数据进行分类、预测等处理.

1.4 评价指标

为了有效的评价LSTM神经网络的预测效果，本文将预测出来的结果与CAS发布的值进行比较，并采用平均绝对误差(mean absolute deviation，MAE)、均方根误差(root mean squared error，RMSE)和精确度P三个性能指标来评估模型的性能. 三个性能指标[17]的定义分别为：

2 数据处理与结果分析

2.1 太阳风暴以及地磁指数分析

2020年6月23日之后BDS-3正式开通，时至2021年底组网完成仅一年半左右的时间，因此本文选取采用的是德国地学中心(Helmholtz-Centre Potsdam-German Research Centre for Geosciences，GFZ)

发布的2021年的太阳辐射指数数据和地磁指数数据进行分析[18]. 表1和表2为太阳辐射通量和地磁指数AP指数的等级划分，图2表示太阳辐射指数F10.7和平均地磁AP指数的2021年的时间变化序列，由图2可知，太阳活动水平和地磁扰动强度都处于比较活跃的状态，其中太阳辐射通量幅值有116 d大于90 d，地磁指数幅值有137 d大于7 d，这表明地球磁场处于扰动和活跃状态. 尤其是在下半年，太阳辐射通量和地磁指数都发生比较大的变化，其中在2021年5月13日和11月4至5日发生了大地磁暴事件. 这意味着电离层同样也会产生比较大的扰动.与此同时，对于北斗卫星的DCB产品的稳定性会产生一定的影响，因此如何准确的预报的带卫星的DCB在不同空间天气状态下的是非常有必要的.

表1 太阳辐射通量等级划分

表2 地磁活动AP指数等级划分

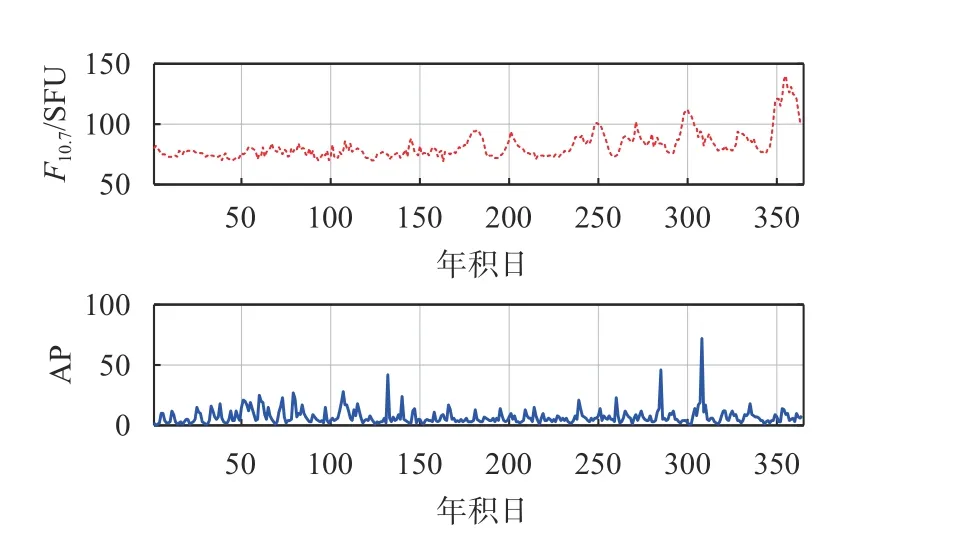
图2 2021年太阳辐射通量F10.7和地磁指数AP时序变化

2.2 BDS-3 DCB时序分析

CAS发布的DCB产品包括八种，本文主要对BDS-3新信号的C1X-C5X，C1X-C6I，C1X-C7Z，C1XC8X四个频间偏差进行分析. 本文选取的是CAS发布的2021年的年积日001—359中BDS-3未发生跳变时的DCB日产品，其时间序列绘图如图3所示. 不难看出，大部分时间BDS-3 DCB值变化不大，都在±0.3 ns内. 但是当卫星数目发生变化的时候，由于约束条件发生了改变，卫星DCB的值会出现较大的波动. 这是由于在分离卫星和接收机端的DCB，通常采用“零均值”约束，即所有卫星端的DCB之和为0[19-20]. 不同时间的DCB会受到卫星数量变化的影响，当某一天的卫星由于一些原因不参与解算而舍弃时，其卫星约束基准会发生变化，因此需要将不同时间的DCB的基准进行统一. 重新实现零基准继续约束后，将其中缺失的卫星DCB值被看作0，实际上这样的值是不符合逻辑的和实际情况的，会对导航定位产生较大的误差. 因此在卫星未出现失效、更新和加入新的卫星时，实现对已有产品中缺失的情况进行改进，精确估计缺失的卫星DCB值，具有重要意义.

图3 2021年的年积日001—359 BDS-3 DCB的时间序列

2.3 BDS-3DCB的预测

2.3.1 LSTM-多项式插值法

为了分析LSTM神经网络的预测效果，本文以BDS-3 C1X-C7Z频间偏差为例. 以2021年年积日001—310 d的CAS发布的DCB产品和GFZ发布的太阳辐射通量和地磁指数作为实验数据. 因此需要设置两个输入层，设置5个隐含层和1个输出层，训练次数选择100次，采用自适应学习率，其中选取310 d的数据作为训练样本，预测7 d的数据并将与多项式预测模型进行对比.

由图4和图5可知，LSTM和多项式拟合法两种模型对BDS-3 DCB的预测都有比较好的效果，MAE均小于0.2 ns，RMSE均小于0.5 ns. LSTM神经网络的预测效果总体要优于多项式拟合法，LSTM的MAE相较多项式拟合法要小约0.04 ns，RMSE要小约0.22 ns. 倾斜地球同步轨道(inclined geosynchronous orbit，IGSO)卫星的误差相较于中地球轨道(medium earth orbit，MEO)卫星保持在比较低的水平上，这是由于训练的样本的值较为稳定，此外还应该得益于IGSO卫星的信号抗干扰遮挡能力强、稳定性最好的结果.

图4 LSTM预测结果与多项式拟合法预测结果MAE比较

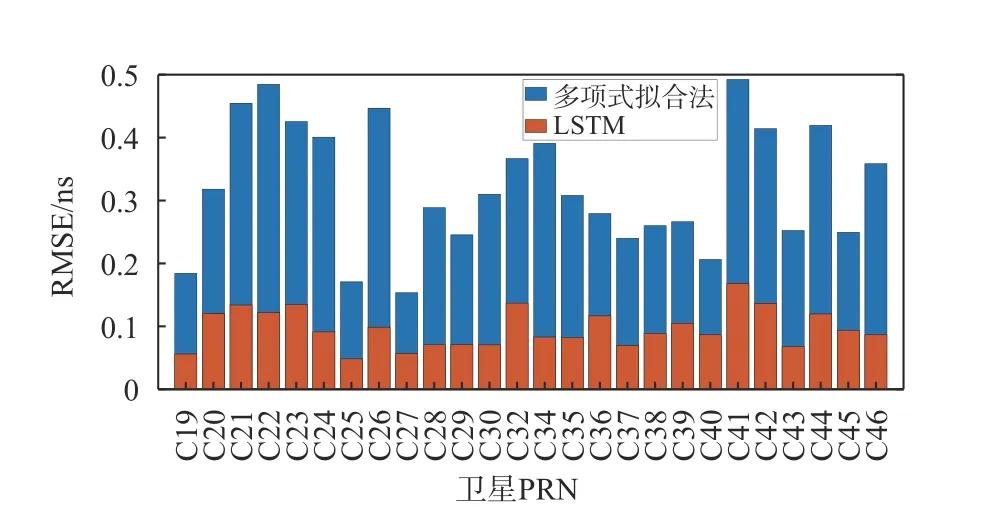
图5 LSTM预测结果与多项式拟合法预测结果RMSE比较

2.3.2 不同时长的LSTM预测

此外为了进一步验证时间对LSTM神经网络的预测效果影响，本文调整预测时长，分别预测7 d、15 d和30 d卫星DCB值，图6为使用LSTM神经网络进行预测7 d、15 d和30 d的MAE和RMSE. 由图6可知，不同天数的预报效果，MAE均小于0.15 ns，RMSE小于0.2 ns，其误差并没有随着天数的增加而发生较大的变动. 其中IGSO卫星的预测效果较其他卫星相对稳定. C41号卫星的预测误差较大，效果相对不理想，图3时间序列中可以看到C41号卫星DCB的值相对较大，在27 ns左右，其数值变化较其他卫星较大，因此在预测时的效果相对较弱. 训练样本的差异过大对未来的数值进行预测时会同样会产生较大误差，因此训练样本的稳定性也会预测效果产生比较大影响.

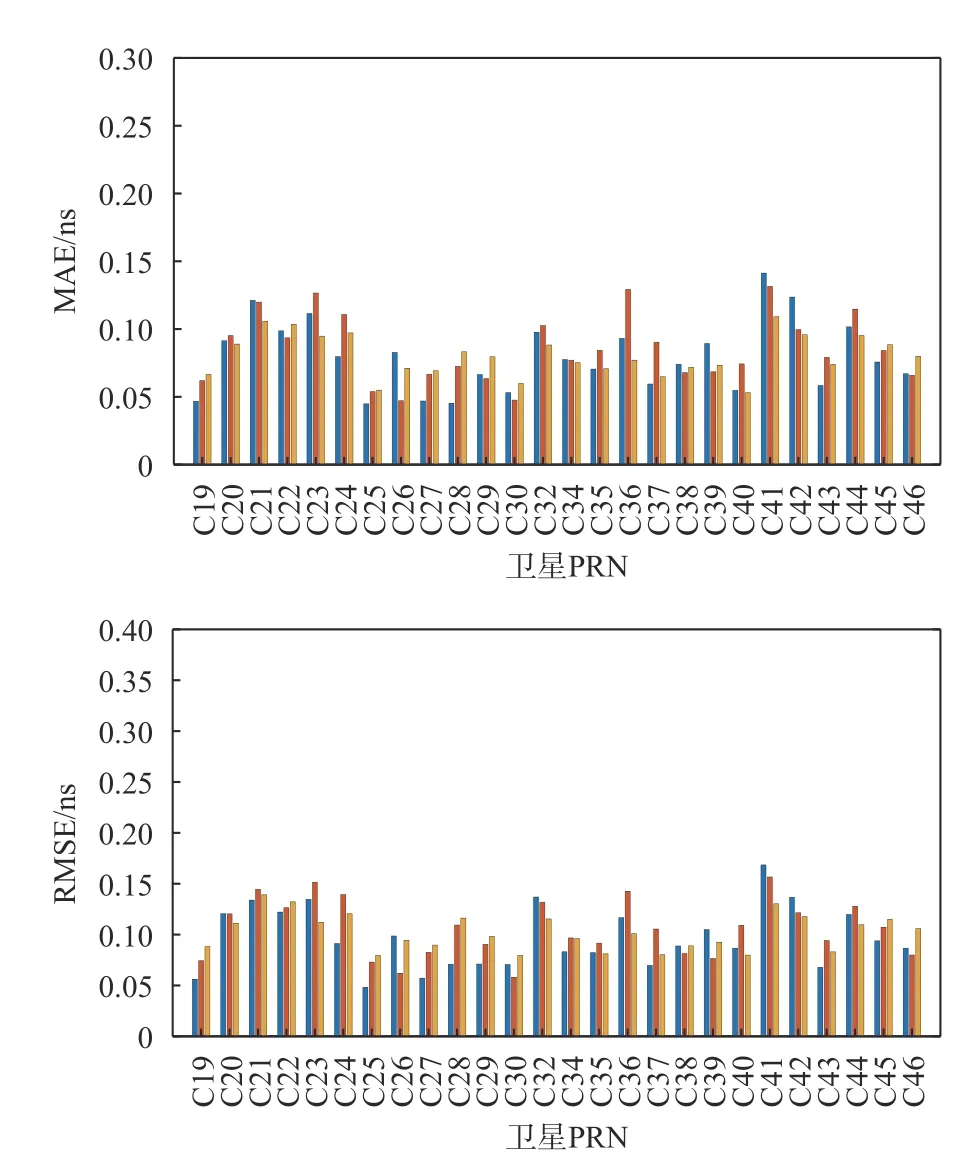
图6 LSTM模型预报不同天数结果对比

选取BDS-3中MEO卫星C25、IGSO卫星C40的四个频率不同天的预测结果进行对比，其精确度结果如表3所示. 可以看到相同频率下，IGSO卫星的精确度较MEO卫星稍低，但精确度均保持在95%以上；不同天数的预测精确度相似，较为稳定. 同一卫星的不同频率的精确度相差较小. 总上所述，LSTM对于不同卫星轨道，不同频率的DCB均有较高的预测精度.

表3 不同轨道卫星DCB预测精度对比%

3 结束语

本文通过CAS发布的2021年的年积日001—310 d的DCB产品作为训练样本，采用LSTM神经网络BDS-3 DCB进行预报和分析. 实验结果表明，通过LSTM神经网络进行预测，效果优于多项式拟合的方法，可以有效的对卫星DCB实现多天的预测. 尽管2021年太阳和地球磁场都比较活跃，LSTM神经网络模型对卫星DCB仍然可以实现比较好的预测效果. 当卫星DCB产品缺失，基准发生改变而引起的DCB值得波动时，LSTM神经网络预测的结果与CAS发布的产品值的MAE与RMSE均保持较低的水平，拟合效果精度高.