联合神经网络和对角加载的GNSS中断定位算法

卢丹，高鹏桦

( 中国民航大学 电子信息与自动化学院, 天津 300300 )

0 引言

捷联惯性导航系统(strapdown inertial navigation system, SINS)[1]与GNSS[2]是最常见的两种定位系统. 而GNSS/INS组合导航系统[3]也是目前应用最广泛、性能最优越的组合导航系统，在航空、航海、车辆等领域发挥着不可或缺的作用，通常利用卡尔曼滤波(Kalman filter, KF)将GNSS和INS的数据进行融合. 但是当载体处于城市高楼密集区、山区、隧道等恶劣环境中时，卫星信号会失锁或者完全丢失[4]，不能获得量测矩阵，因此无法进行KF这一过程，GNSS/INS组合导航系统仅依靠INS单独工作，导航定位结果会迅速发散[5]，导航性能严重恶化，这也是目前组合导航系统应用中亟须解决的问题.

近年来，越来越多的学者利用人工神经网络(artificial neural network, ANN)[6-7]辅助组合导航进行信息融合. 应用最简单的是利用反向传播(back propagation，BP)神经网络辅助组合导航系统[8]，当卫星信号中断时，通过网络输出校正INS位置. 此外还有多层感知器神经网络[9]、径向基神经网络[10](radial basis function neural network, RBFNN)、Elman神经网络[11-12]等. 这些算法主要以KF的估计值作为网络的训练目标，并利用神经网络的预测结果直接取代KF，这就放弃了由INS原理推导的系统显式误差模型；或者利用神经网络预测GNSS信号中断时丢失的量测参数，以便KF继续进行，但是也无法模拟在卫星信号丢失过程中INS的位置与速度误差趋势，因此在GNSS中断较长时间情况下，得不到较为可靠的导航定位信息. 考虑到组合导航系统是一个连续的时间序列，将当前时刻的网络输出与载体过去时刻的位置信息结合起来，利用自适应神经模糊推理系统[13-14](adaptive neuro-fuzzy inference system，ANFIS)、循环神经网络(recurrent neural networks，RNN)[15]等具有记忆功能的动态网络来辅助组合导航系统，在卫星信号中断时获得较好的定位结果. 由于算法自身性能较好，但本质上与BP类辅助算法类似，直接取代KF或间接辅助KF，并没有紧密结合KF来分析神经网络的训练误差对组合导航算法的影响. 并且这些算法在参数优化方面存在不足，导致训练次数过多、训练时间长，不适合实时应用.

上述方法结果证明了在卫星信号中断期间，神经网络可以通过学习惯性传感器的输出与真实位置之间的关系来进行预测，从而提高定位精度. 由于INS系统本身特性使上一时间预先训练的网络模型存在误差，中断时刻INS误差仍不断累积，因此，本文利用BP神经网络辅助组合导航，当卫星信号失锁时，分析训练误差对组合导航算法的影响，通过对角加载重构GNSS/INS组合导航中量测噪声协方差矩阵进行KF更新，使得GNSS信号在长时间中断期间，导航系统仍拥有较为可靠的导航性能.

1 传统BP神经网络辅助组合导航

1.1 滤波的状态方程和量测方程

以SINS的姿态误差、速度误差、位置误差、角速度误差、比力误差15×1的列向量作为松耦合导航系统的状态变量，即

状态方程可表示为

其中：F为15×15的SINS误差状态量系数矩阵，根据INS的位置、速度与姿态误差方程计算得到[16]；G为15×6的SINS噪声分配矩阵；w为6×1的系统噪声矩阵. 系统噪声分配矩阵G的表达式为

在GNSS/INS松组合导航系统中，采用SINS解算的位置和速度与GNSS测量到的位置和速度之差作为量测信息[17]. 得到松组合导航系统的量测方程为

式中： δPK与 δVK为东、北、天坐标系下INS的位置与速度误差；为GNSS的定位误差，分布规律为0均值，协方差矩阵为的高斯白噪声，即：.

INS在东、北、天坐标系下的位置误差 δPK与纬度、经度、高度下的位置误差 δPLLH，存在转换关系如下：

其中， ψ 的表达式为

式中：L为经纬高坐标系下的纬度；RM与RN分别为子午圈半径、卯酉圈半径.

Hk是6×15的观测矩阵，具体表达式为

至此建立了KF的状态模型和量测模型，当卫星信号正常时，利用GNSS观测量不断修正惯导解算结果.

1.2 传统神经网络辅助算法

基于KF的GNSS/INS组合导航系统利用了GNSS和INS各自优点可为移动载体提供连续可靠的导航定位信息. 但由于外部干扰或当载体处于恶劣环境时，卫星信号质量下降甚至直接丢失，系统因无法得到量测矩阵Zk，导航性能迅速下降. 因此利用BP神经网络辅助组合导航系统，达到卫星信号中断期间内仍可获得较为可靠的导航性能的目的. 传统的神经网络辅助组合导航系统分为训练模式与预测模式两个阶段，如图1所示.

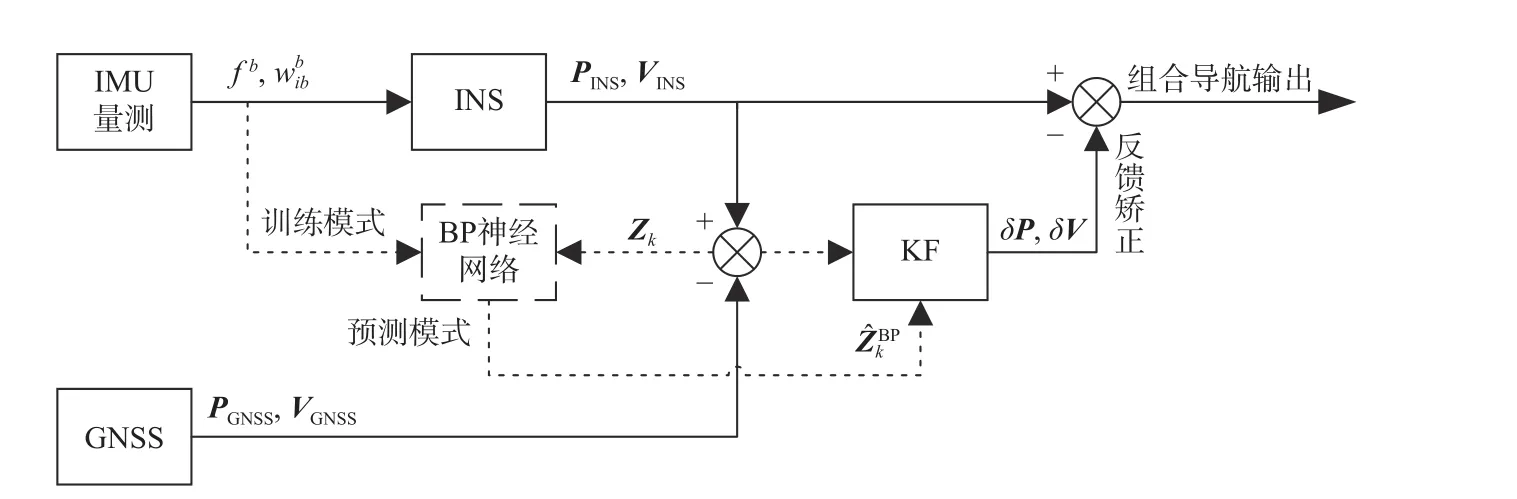
图1 传统神经网络辅助组合导航原理框图

当卫星信号可用时，选择加速度计fb和陀螺仪的输出作为BP神经网络的输入，将滤波时的量测值Zk作为网络的训练目标，系统进入训练模式，并不断优化网络参数；当信号中断时，可利用训练好的网络得到，作为KF器的量测矩阵来校正INS输出.因此神经网络的输入输出关系可表示为

然而，由于BP神经网络模型与INS误差模型的特性，利用人工神经网络只能部分补偿INS带来的误差. 在卫星信号失锁期间，INS误差仍不断累积，导致中断后经网络预测得到的量测值与参考值存在一定的误差，这也是目前神经网络在卫星信号中断时辅助组合导航系统定位效果并不理想的主要原因.

2 基于对角加载的更新算法

在卫星信号失锁期间，中断后由于INS的累计误差导致经网络预测得到的量测值小于参考值. 设定误差值为Ek，且为负值，所以网络预测过程中，量测值如式(9)所示：

将式(4)代入式(9)可得

因此GNSS中断时，由传统神经网络辅助KF时，原量测噪声协方差矩阵存在误差. 由式(11)可知，更新后的协方差矩阵相当于矩阵的对角加载得到. 并且由于误差Ek是由中断后INS累计误差造成，所以 λ 的取值可为：

其中：w1为加速度计常值漂移；w2为陀螺仪常值漂移；T为信号中断时长. 并将上述构建的噪声协方差矩阵代入滤波过程.

GNSS中断时，基于对角加载来重构噪声协方差矩阵(reconstruct the covariance matrix，RCM)为中断时刻的滤波量测矩阵，新的对角加载KF迭代方程如下：

预测方程：

状态更新方程：

本文结合BP神经网络，通过矩阵对角加载的方法，重构量测噪声协方差矩阵，并更新中断时刻的KF算法定义为BP-RCMKF，其工作流程分为两部分：第一部分为GNSS信号可用时，网络在线学习的训练模式；第二部分是当GNSS信号中断时，网络根据上一时刻的训练结果重构量测噪声协方差矩阵，更新KF方程. 具体工作原理如图2、图3所示.

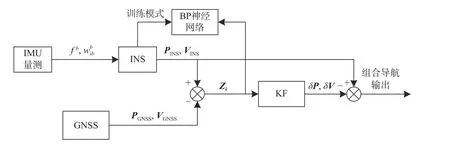
图2 神经网络辅助组合导航训练模式框图

图3 神经网络辅助组合导航预测模式框图

当GNSS卫星信号可用时，GNSS数据可通过与INS位置/速度信息做差值来提供测量值Zk，神经网络辅助组合导航系统以训练更新模式工作，如图2所示，将获得的Zk作为网络目标，并选择加速度计和陀螺仪的输出作为网络输入. 在GNSS工作良好的情况下，利用目标数据在线更新神经网络参数. 当GNSS信号发生中断时，神经网络辅助组合导航系统切换到预测模式. 如图3所示，中断时的陀螺仪和加速度计的量测值作为神经网络的输入参数，来预测中断时的量测，同时由于BP网络预测值与真实值的误差关系，加入量测误差模型Ek，并重构量测噪声协方差矩阵，进行对角加载KF.

3 仿真实验

模拟一段时间为1200 s的飞行轨迹，飞行的起始位置为(116°E，40°N)，高度为1000 m，通过GNSS模拟器生成GNSS卫星信号，并由软件接收机得到GNSS的位置信息，飞行轨迹如图4所示. 人为设置GNSS信号在600～800 s中断，来验证新方法的有效性.

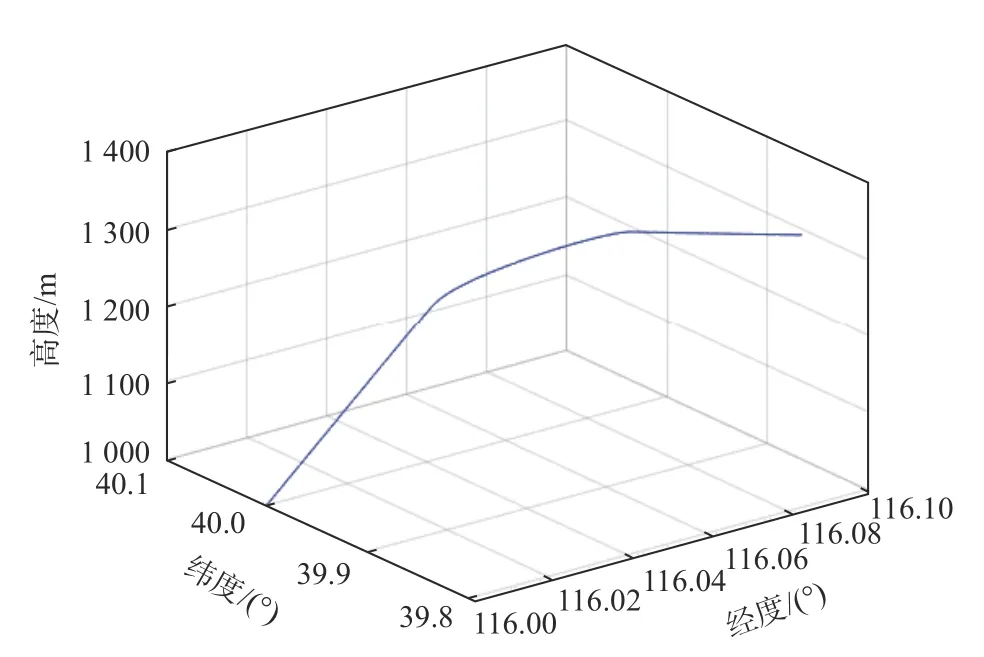
图4 飞行轨迹图

设置INS误差参数如表1所示. 选择用BP神经网络来辅助卫星信号中断时的组合导航系统，BP神经网络的参数如表2所示，其中网络的输入样本为陀螺仪和加速度计的输出，网络的输出目标为KF量测值Zk，隐藏层神经元的个数根据经验公式选择为13并进行网络训练.

表1 INS误差参数

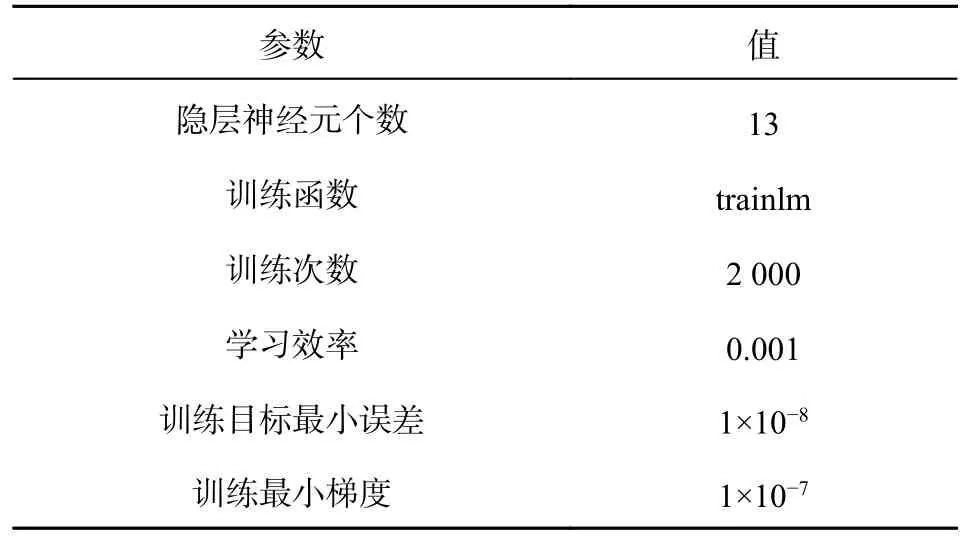
表2 BP神经网络参数设置

通过传统神经网络预测来辅助组合导航系统，BP神经网络辅助KF校正INS误差，在600～800 s的GNSS卫星信号中断期间，由网络预测得到的量测值与假设未中断时参考值存在误差，如图5所示，图中展示了这两个量测值在位置分量上的误差.

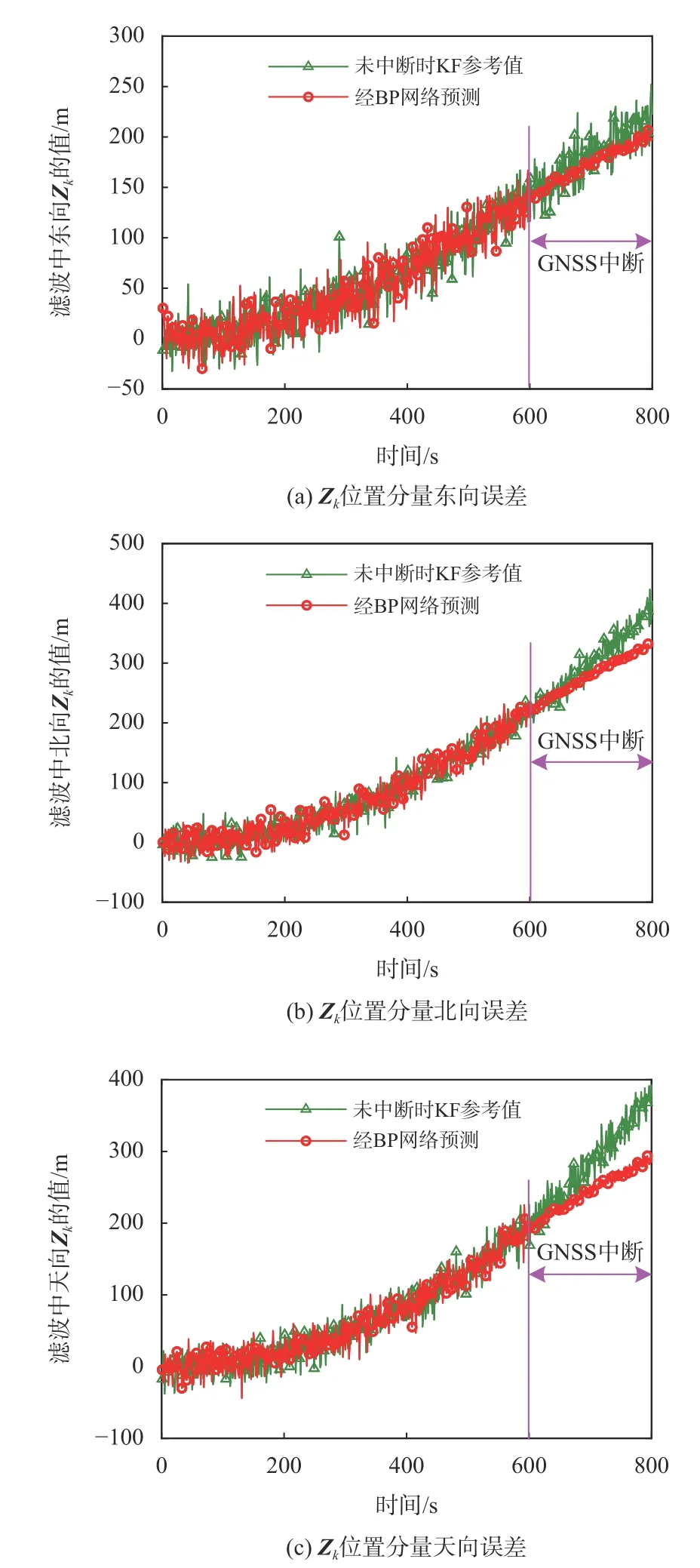
图5 网络预测的量测值与参考值对比

仿真进行了500次蒙特卡洛实验，得到了经过不同方法BP神经网络辅助组合导航系统在遭遇GNSS卫星信号失锁及其恢复情况下的定位误差，如图6所示. 在600～800 s卫星信号中断200 s期间，在传统方法由纯INS工作方式下，导航误差迅速增大，经过BP网络辅助组合导航系统后定位误差均得到改善，验证神经网络辅助算法的有效性. 由于神经网络的训练目标为INS的位置、速度误差，代替KF器直接对INS进行校正，BP代替KF算法导航结果并不理想；采用BP-KF算法并不能很好的处理中断时INS的累计误差；通过重构量测噪声协方差矩阵，更新KF流程，提出的BP-RCMKF重构量测噪声协方差矩阵辅助算法的导航定位效果更好，并且在801 s GNSS中断恢复后，定位误差可以在较短的时间内恢复到正常情况.

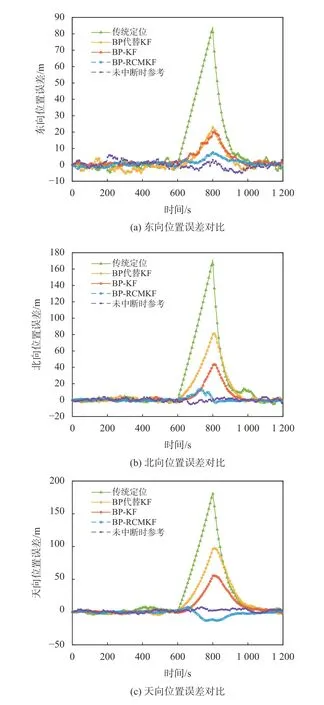
图6 不同预测方法下导航定位误差对比

在200 s中断时长内，通过BP-RCMKF神经网络预测辅助组合导航系统的定位效果有明显改善. 如表3所示，列出了在不同辅助方法下位置误差的均值与均方根的值. 其中，东向位置误差降低了93.11%，北向位置误差降低了92.27%，天向位置误差降低92.13%；本文提出的BP-RCMKF算法在东向、北向与天向定位误差最大值分别为8.47 m、16.74 m、13.17 m，东向、北向与天向定位误差的均方根值分别为3.33 m、7.43 m、7.89 m，与BP-KF相比东向位置误差降低了59.98%，北向位置误差降低了37.35%，天向位置误差降低了67.82%.

表3 不同辅助方法下位置误差统计特性m

进一步对比不同辅助方法，进行了500次的蒙特卡洛实验，对GNSS卫星信号从短时间中断到长时间中断情况下的定位误差进行统计，如图7所示. 如图7(b)中，中断40 s时，由于中断时间较短造成经BP网络预测的量测值误差较小，导致重构量测噪声协方差矩阵方法效果不明显，但在卫星信号失锁较长时间时，重构量测噪声协方差矩阵的辅助算法在实验中东、北、天向均方根误差更小，验证了BP-RCMKF算法的有效性.

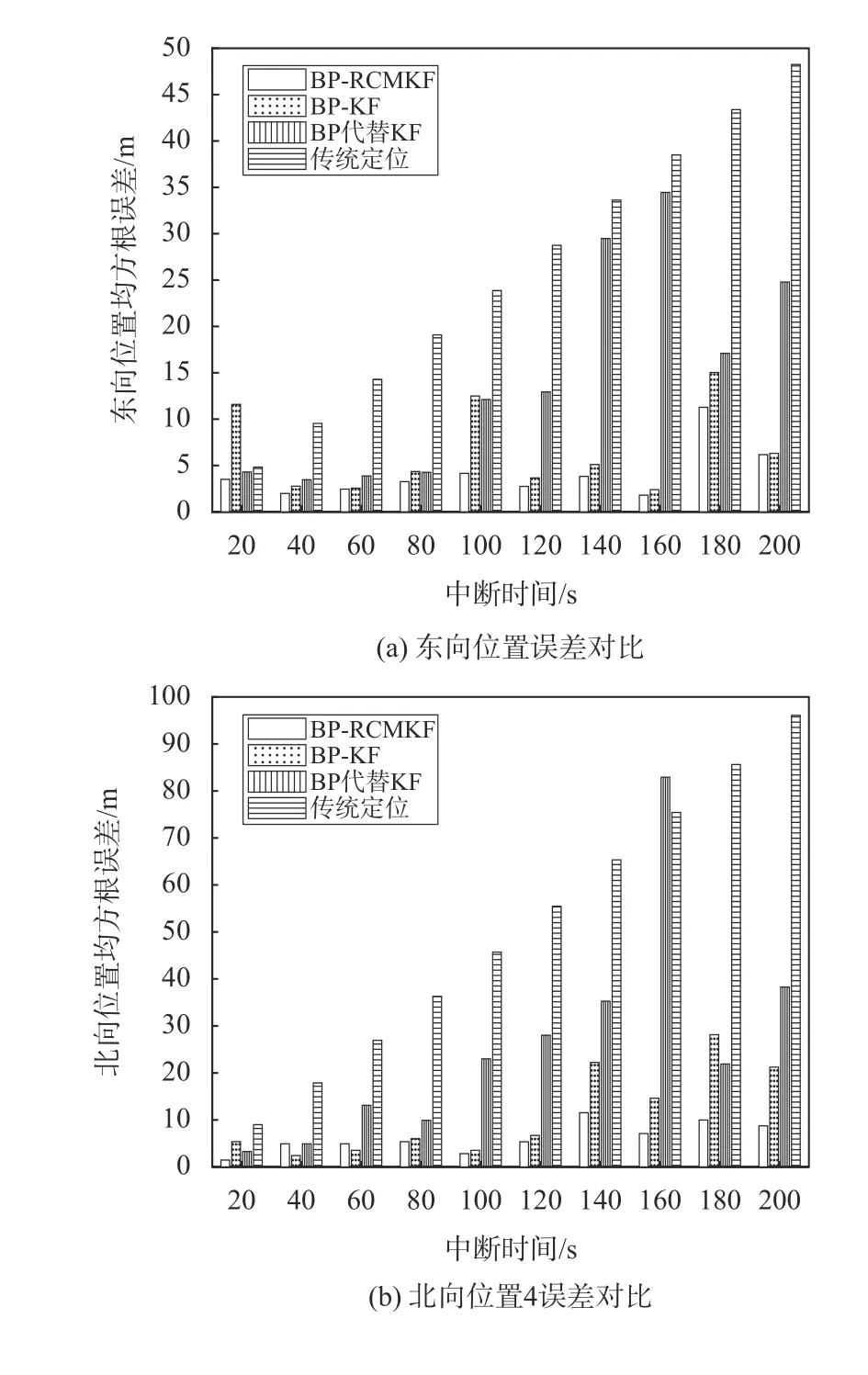
图7 不同中断时间下各种辅助方法的定位误差对比

4 结束语

基于INS的误差模型与神经网络的预测模型分析，本文提出了一种基于BP神经网络辅助组合导航系统的BP-RCMKF改进算法来弥补GNSS卫星信号中断期间迅速增大的定位误差. 经过仿真实验分析可得，提出的重构量测噪声协方差阵更新KF的方法能够弥补GNSS失锁时由INS单独工作带来的累计误差，有效降低卫星信号中断期间的导航定位误差，达到较好的导航定位性能.