基于L1/2正则化的抛物线Radon变换多次波压制方法

吴秋莹 胡斌 刘财 高锐

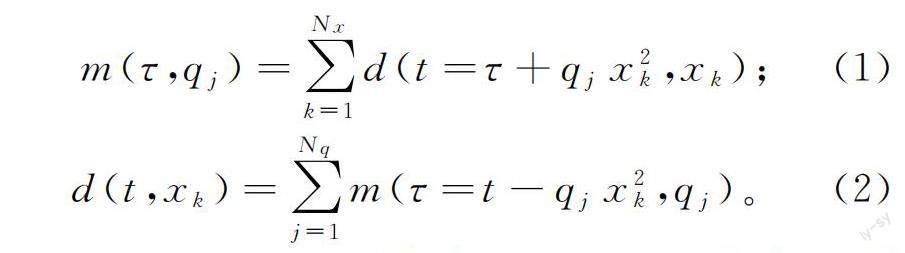
摘要：在地震數据处理中，多次波的存在会对地震数据成像和地震资料解释带来影响，如何有效地压制多次波干扰是地震勘探中的重要问题。抛物线Radon变换因其高效的特点被广泛应用于多次波压制中，但在野外地震数据采集时，炮检距的有限性会导致变换域中的能量扩散，产生假象，使多次波压制达不到理想的效果。针对此问题，提出一种基于L_1/2正则化的稀疏反演高分辨抛物线Radon变换，并应用广义迭代收缩算法（generalized iterated shrinkage algorithm， GISA）进行求解。研究结果表明，L_1/2正则化有很强的稀疏约束能力，能提高解的稀疏度，改进信噪分离的效果。与最小二乘反演和基于L₁正则化的稀疏反演相比，基于L_1/2正则化的稀疏反演高分辨抛物线Radon变换能更有效地压制多次波，并确保了重构数据与原始数据的一致性。

关键词：多次波压制；高分辨率抛物线Radon变换；L_1/2正则化

doi：10.13278/j.cnki.jjuese.20220307

中图分类号：P631.4

文献标志码：A

收稿日期：2022-11-08

作者简介：吴秋莹（1993—），女，博士研究生，主要从事地震数据处理工作，E-mail： qywu20@mails.jlu.edu.cn

通信作者：刘财（1963—），男，教授，博士生导师，主要从事地震波场正反演理论、综合地球物理等方面研究，E-mail： liucai@jlu.edu.cn

基金项目：国家自然科学基金项目（41874125）

Supported by the National Natural Science Foundation of China （41874125）

Multiple Suppression Method of Parabolic Radon Transform

Based on L_1/2RegularizationWu Qiuying ¹， Hu Bin¹， Liu Cai¹， Gao Rui^2，3

1. College of GeoExploration Science and Technology， Jilin University， Changchun 130026， China

2. School of Earth Sciences and Engineering， Sun Yat-Sen University， Guangzhou 510275， China

3. Key Laboratory of Deep-Earth Dynamics of Ministry of Natural Resources， Institute of Geology， Chinese Academy of

Geological Sciences， Beijing 100037， China

Abstract： In the context of seismic data processing， the presence of multiples poses inherent challenges to the imaging and interpretation of seismic data. The effective suppression of these multiples stands as a key issue in seismic exploration. Leveraging its high efficiency， the parabolic Radon transform emerges as a widely used technique for multiple suppression. However， in field seismic data acqisition， due to the limited offset， energy diffusion and illusions reduce the effect of multiple suppression in the Radon domain. In response to this challenge， we propose a L_1/2-regularized high-resolution parabolic Radon transform with sparse inversion， where the inverse problem is solved by  generalized iterated shrinkage algorithm （GISA）. The L_1/2 regularization chosen for its robust sparse constraint capabilities plays an important role in enhancing the solution sparsity and improving the signal-noise separation. Compared with the least square inversion and the sparse inversion method based on L₁regularization， the L_1/2-regularized sparse inversion of using the high-resolution parabolic Radon transform can suppress multiples effectively and ensure the consistency between the reconstructed data and the original data.

Key words： multiple suppression; high-resolution parabolic Radon transform; L_1/2regularization

0 引言

多次波在反射波地震勘探中通常被视为干扰波，较强的多次波会影响深层一次波的成像效果，在地震资料解释中造成误解。因此，针对压制多次波的问题，国内外学者对此做了大量的研究。压制多次波的方法一般可分为两个类别^[1-2]：一是滤波类方法，这类方法基于一次波和多次波的周期性、空间特性等差异来压制多次波，常用的方法有预测反褶积^[3]、Radon域滤波^[4]、f-k（频率-波数）域滤波^[5]、聚束滤波^[6]等；二是预测相减类方法，这类方法是对多次波进行预测并从地震记录中减去，常用的方法有逆散射级数法^[7]、波场延拓法^[8]、自由表面多次波压制法^[9-10]等。由于一次反射波与具有相同法线时间的多次反射波相比，传播速度更高，两者同相轴之间存在明显差异，当一次波和多次波间的速度差异较大时，滤波方法能有效且高效地压制多次波。由于一次反射和多次反射在τ-q（截距-曲率）域中的分离效果较f-k、τ-p（斜率）域中的分离效果更好，且更高效、成本更低，故抛物线Radon变换被广泛地应用于压制多次波。高分辨率抛物线Radon变换能使一次波和多次波在速度差异较小时也得以分辨。因此，本文研究了抛物线Radon变换及其高分辨率方法。

Radon变换于1917年由Radon提出^[11]，20世纪70年代被引入到地球物理领域。1986年，Hampson^[4]利用抛物线Radon变换在动校正后的共中心点（common middle point， CMP）道集上压制表面多次波，并提出利用最小二乘反演法来优化Radon域的数据，此反演方法减少了抛物线Radon域的模糊现象。然而影响Radon变换分辨率的主要因素包括空间假频、截断误差、保幅性问题等，通常可以应用稀疏反演方法来解决地震数据的稀疏性问题以提高Radon域中的数据分辨率。所以，1995年，Sacchi等^[12]將Radon变换考虑为稀疏反演过程，提高了Radon变换域的分辨率，并将抛物线Radon变换在频率域实行，提高Radon变换的效率。2000年，Herrmann等^[13]利用一种高分辨的抛物线Radon变换区分一次波和多次波，以非迭代的方式处理混叠和分辨率问题，使空间假频的问题得到一定的解决。2009年，熊登等^[14]提出利用混合域的Radon变换压制多次波，提高了计算效率和分辨率。2013年，Li等^[15]利用λ-f域（其中，λ=fq）的Radon变换对多次波压制后的数据进行保幅。2016年，巩向博等^[16]提出混合域双曲线Radon变换多次波压制方法，提高了分辨率和计算效率。

本文重点研究基于稀疏反演的高分辨率Radon变换。稀疏反演问题在求解时，会存在解不唯一的情况，为解决此问题，可以在高分辨率Radon变换基础上加入L范数约束的稀疏约束条件，得到稀疏约束的Radon变换。L₀范数正则化约束具有稀疏性，但其最优化问题求解较困难，可以使用L₁范数替代^[17]。L₁正则化是L₀正则化的最优凸近似，它比L₀正则化容易求解并且更具稀疏性，但已有研究表明L₁正则化并不是最佳的稀疏正则化^[18]。2010年，Xu等^[19]提出了L_1/2正则化，证明了L_1/2正则化可以得到比L₁正则化更稀疏、更稳定的解，是L_p（01/2正则化应用于各种研究中，如2012年Zeng等^[20]用于稀疏雷达成像中、2013年Sun等^[21]用于遥感数据高光谱解混中、2019年康治梁等^[22]用于地震稀疏反褶积中。

本文将L_1/2正则化方法引入抛物线Radon变换压制多次波中，并与L₁正则化方法进行对比，通过模型数据及实际数据验证方法的有效性。

1 基本理论

1.1 抛物线Radon变换

Radon变换多次波压制方法基于一次波和多次波的时差差异，在采用介于一次波与多次波之间的速度对地震数据的CMP道集进行动校正后，同相轴的剩余时差接近抛物线形状，因此经过抛物线Radon变换，可以将一次波和多次波具有不同曲率的同相轴映射到Radon域中的不同区域，以实现一次波与多次波的分离。抛物线Radon变换的求和轨迹沿着抛物线进行，其正反变换的表达式分别为：

式中：d（t，x_k）为地震数据；m（τ，q_j）为抛物线Radon变换后的Radon域数据；x_k为偏移距；N_x为地震道数；t为时间；q_j为曲率参数；N_q为曲率参数的数量。抛物线Radon变换使在时-空域具有抛物线形状的同相轴在抛物线Radon域映射成一个点。

为提高抛物线Radon变换的计算效率，通常对地震剖面沿时间方向进行Fourier变换，其正反变换公式分别为：

式中：f为频率；M（q_j，f）为频率域Radon数据；D（x_k，f）为频率域地震数据。利用式（3）使每个频率成分分别反演，独立进行Radon变换。式（3）和（4）表示为矩阵形式可分别描述为：

m=A^Hd；    （5）

d=Am。    （6）

其中，算子A及其共轭转置A^H分别定义为：

Hampson^[4]采用抛物线Radon变换在CMP道集中压制多次波，并且利用最小二乘反演法，得到最小二乘解为

m=（A^HA）^-1A^Hd。    （9）

通常，为了反演过程的稳定性，在矩阵主对角线上引入阻尼参数α，即

m=（A^HA+αI）^-1A^Hd。    （10）

α一般选择为矩阵A^HA的百分之几。

最小二乘抛物线Radon变换提高了Radon域数据的分辨率以及变换的精度和聚焦能力，使Radon域假象減少，限制部分能量扩散，且确保了重构数据与原始数据的一致性，然而，结果仍然不是最佳的。

影响Radon变换分辨率的主要因素有以下几点^[23]：一是q的取值范围。若q的取值范围较大，则Radon域的能量不能较好地聚焦，产生空间假频问题。q的变化量Δq和最大值q_max应满足^[24]：

式中：x_max为最大跑检距；f_max为信号的最高频率。二是由于炮检距的有限性，能量出现发散现象，使Radon域中的映射不是一个点，而是具有拖尾现象的剪刀状。因此，希望Radon域的解更加稀疏，使x-t域的同相轴在Radon域投影成一个带限的脉冲，应用稀疏反演方法解决地震数据的稀疏性问题，而后优化反演中的稀疏化参数，使同相轴在Radon域有更好的局部化特征，对反演结果不断地进行迭代修改，并优化求解算法，提高Radon域中的数据分辨率。三是噪声。应在保证有效信号不丢失的情况下尽可能地压制噪声，故对信号进行保幅性处理。

1.2 基于L_1/2正则化的抛物线Radon变换

利用L范数作为惩罚项来约束反演目标函数的正则化方法，可以使结果满足稀疏化，保留待反演参数的特征信息，并且求得唯一的稀疏解，从而获得稀疏约束的高分辨率抛物线Radon变换。常用的正则化方法有L₀正则化、L₁正则化、L₂正则化、L_p正则化，用单位球几何形状表示如图1所示。L₀范数表示向量中非零元素的数目，其正则化约束区域没有角（图1a），很难出现零解，所以该方法具有稀疏性，但其求解困难，应用较少；L₁正则化的约束区域是正方形（图1b），该正则化具有对异常值不敏感的特性，是凸优化问题，可以使用增广拉格朗日乘子法^[25]、迭代软阈值法^[26]、迭代重加权最小二乘法^[27]、梯度投影法^[28]等进行求解，能实现较好的稀疏效果；L₂正则化可以避免模型发生过拟合现象，但其约束区域没有角（图1c），很难出现零解，可以避免模型发生过拟合现象，但没有L₁正则化稀疏。

Chartrand等^[18]在压缩感知方面对L₁正则化优化问题进行研究的实验数据表明，L_p（01正则化能从更少的观测数据中恢复稀疏信号，信号恢复能力更强、更稳定、有更低的预测误差。Xu等^[19]系统研究了L_p（01/2正则化问题。如图1d所示，L_1/2正则化的解出现在拐角处，表明比L₁正则化更稀疏。研究表明，当1/2≤p<1时，L_1/2正则化是L_p正则化中最稀疏的；当0p正则化具有与L_1/2正则化相似的性质，p的取值对稀疏解的影响不大^[19]。所以说L_1/2正则化是L_p（0

L_1/2正则化的最优化问题可表示为

L_p（0

根据GISA，式（14）的迭代解可表示为：

m_k+1=GST（θ_k+1，ξμ，p）;    （15）

θ_k+1=m_k-μA^H（Am_k-d）。    （16）

式中：m_k为迭代k次的迭代解；ξ为迭代步长；GST（·）为广义软阈值算子，定义为

式中，sgn（·）为符号函数。

为了加速算法的收敛性，采用Beck等^[32]提出的快速收敛策略，将Nesterov加速算法引入到GISA中：

此方法提高了反演的收敛速度以及计算效率。最终得到m︿，获得了抛物线Radon变换更具稀疏性、且高分辨率的结果，达到理想的多次波压制效果。

2 正演模型测试

为验证以上理论，利用模拟地震记录进行模型测试。模拟数据理论模型为八层水平层状速度模型（图2）。时间方向有500个采样点，采样间隔为4 ms，空间方向上为126道，偏移距为0～3 150 m，道间距25 m。图3为动校正前后的CMP道集。从原始CMP道集（图3a）中可以观察到多条一次波和一系列多次波，多次波集中在中下部0.6～2.0 s。从经过动校正后的CMP道集（图3b）中可以看出，由于多次波的速度较相同法线时间一次波的速度更低，所以在CMP道集中按照一次波速度动校正后，一次波被拉平，而多次波因校正不足，呈现下拉的状态，使多次波同相轴剩余时差更接近抛物线形态。在图3b中观察到的下拉状态的同相轴均为多次波。

利用传统最小二乘抛物线Radon变换方法和基于L₁正则化的抛物线Radon变换方法作为对比组，以验证本文方法在多次波压制方面的效果。从图4可以看出，经过抛物线Radon变换后，一次波分布在q=0附近和q＜0区域，多次波分布在q＞0区域。利用最小二乘抛物线Radon变换得到的Radon域数据，同相轴在Radon域中没有较好地聚成一点，产生较多假象（图4a）；利用基于L₁正则化抛物线Radon变换得到的Radon域数据假象减少，但效果并不理想（图4b）；使用基于L_1/2正则化抛物线Radon变换得到的Radon域数据（图4c），比图4b的“拖尾”效应得到明显的改善，能量更汇聚，数据变换精度和聚焦能力得到进一步提高。

接下来，在Radon域中切除多次波所在的q＞0区域，再变换回时-空域，得到只有一次波的动校正后的CMP道集，再经过反动校正，得到压制多次波后的CMP道集。

将多次波压制结果与不含多次波的波场进行对比，结果如图5所示。可以看出：最小二乘抛物线Radon变换（图5b）和基于L₁正则化的抛物线Radon变换（图5c）的多次波压制结果在0.7、1.2以及1.6 s处仍有一些残余的多次波能量；本文方法的多次波压制结果在相同位置几乎没有残余的多次波（图5d）。

通过速度谱对结果进行进一步对比。图6为本文方法压制多次波前后的速度谱，从中可以明显看到，时间在0.8～2.0 s、速度在2 000 m/s的多次波能量得到了较好的压制，而一次波的能量得以保留，利于更准确地识别速度信息。

综上，在基于3种算法的抛物线Radon变换压制多次波中，本文方法能获得最稀疏的解，使多次波得到极好的压制，并且也能有效保护一次波的振幅，具有一定程度的保幅性。

为测试本文方法的抗噪能力，以S_NR=m/（m-m-）作为信噪比（m为不含噪声信号，m-为含噪声信号）。分别以信噪比为5、-5、-15 dB加入到某一模型数据中，得到不同信噪比的正演模型数据。利用本文方法对数据进行重建，结果如图7所示，不同信噪比数据的重构误差如表1所示。

由图7、表1可知，即使噪声较强，对重建数据也并没有过大影响；可以证明本文方法的抗噪能力较强，能够实现具有抗噪性能的多次波压制。

3 实际数据处理

為进一步验证本文方法，采用某海上实际数据动校正后的CMP道集（图8）进行多次波压制处理。时间方向上有1 305个采样点，截取3.2～4.8 s多次波较多的部分进行多次波压制，该部分数据在时间方向上有400个采样点，采样间隔为4 ms，空间方向上为92道，道间距为175 m，偏移距为16 100 m。实际数据中较深层位置3.8～4.8 s处存在大量的多次波，导致一次波数据被掩盖，影响一次波成像效果。

图9为利用3种算法得到的Radon域数据，可以看出，本文方法处理的Radon域数据（图9c）与最小二乘抛物线Radon变换（图9a）和基于L₁正则化的抛物线Radon变换（图9b）相比具有更高的分辨率，能量聚焦明显且假象明显较少。

图10为多次波压制结果。将3种方法的多次波压制结果（图10b、c、d）与动校正后的原始CMP道集（图10a）进行对比，可以看到本文方法（图10d）的压制结果优于最小二乘抛物线Radon变换（图10b）和基于L₁正则化的抛物线Radon变换（图10c）：在3.8～4.2 s和4.4～4.7 s处，图10b和图10c明显有大量的多次波残留，而且由于近偏移距处的多次波和一次波速度相近，在Radon域切除q＞0区域时，也会影响一次波的投影区域，使近偏移距损失了部分一次波能量；而本文方法的一次波能量得到了一定的保护（图10d），并且在3.8～4.2 s和4.4～4.7 s处没有明显的多次波残留。

图11a、b为分别利用基于L₁正则化和L_1/2正则化Radon变换后又经Radon反变换重构的地震数据，对比图11a、b可以直观地看出，本文方法的重构数据连续性更强，且与原始数据（图10a）具有更强的一致性。

利用重构误差定量分析重构数据^[33]与原始数据的一致性：

式中：m为原始数据；m′为重构数据；s为重构误差。经计算，求得基于L₁正则化和L_1/2正则化的抛物线Radon变换重构误差分别为：s_L1=15%，s_L1/2=8%。实际数据的波场较为复杂，含有其他噪声，本文方法的重构数据比基于L₁正则化抛物线Radon变换的方法更逼近原始数据。

图12为压制多次波前后3种方法的单道对比，可以进一步对比多次波压制效果。截取了3.7～4.8 s处多次波较丰富的部分，可以直观地看到，利较小，直观地证明了本文方法的有效性。

4 讨论

随着三维地震勘探技术的日益发展，三维地震数据处理也被广泛关注。为验证本文方法对三维资料的实用性，我们模拟生成了三维地震数据的CMP道集。纵测线偏移距范围为-5 000～5 000 m，联络测线方向偏移距范围为-2 500～2 500 m，多次波剩余时差分别为600、400、200、60 ms，振幅分别为-1.0、0.5、0.1、-0.9。图13a为从三维模拟数据中抽取的5个含多次波的三维小面源CMP道集，图13b为对应的按标量偏移距大小排列的三维CMP道集，可以清晰地看到多次波的存在（箭头处）。

利用最小二乘抛物线Radon变换、基于L₁正则化的抛物线Radon变换以及文中提出的基于L_1/2正则化的抛物线Radon变换对以上数据进行多次波压制，结果如图14所示。最小二乘抛物线Radon变换（图14a）和基于L₁正则化的抛物线Radon变换（图14b）的Radon数据中可以看到较多的假象，同相轴没有很好地聚成一点；而本文方法的Radon域数据（图14c）能量聚焦明显，假象减少。

压制多次波后的最终结果如图15所示，可以清晰地看到图15a、b中都未见多次波残留，并且一次波同相轴未被影响，得到了较好的多次波压制结果。

三维实际数据的多次波压制问题将会在后续的研究中继续进行。

5 结论与展望

本文系统阐述了抛物线Radon域压制多次波的方法，提出了利用基于L_1/2正则化的抛物线Radon变换多次波压制方法，得到以下结论：

1）由于L_1/2正则化可以获得比L₁正则化更稀疏的解，所以基于L_1/2正则化的稀疏反演Radon变换具有更高的分辨率。

2）理论模型和实际数据结果证明本文方法具有较高的分辨率，重构的地震数据与原始数据有更高的一致性，提高了多次波压制的效果，减少了有用信号能量受到不必要的损失，为后续的一次波成像提供高质量的数据基础。

但在复杂地质条件下，由于波场中微弱的有效信号容易被噪声覆盖，所以参数的设置需要更加谨慎，否则可能会因为压制噪声而损失有效信号。另外，由于本文方法应用L_1/2范数，虽然提高了地震信号的稀疏性，但使计算时间增加，所以此方法的计算效率相比于L₁范数方法没有较大优势。而且由于提高了反演精度，会对地震数据的保幅性有较高的要求，所以针对以上局限性我们将会从以下三方面进行改进：

1）将考虑地震数据的振幅与偏移距的特征（amplitude versus offset， AVO），将本文方法与正交多项式变换相结合。

2）对求解算法进行进一步改进，提高算法的计算效率。

3）将本文方法与其他多次波压制方法相结合，对复杂地质条件的地震资料进行高效率高质量的处理。另外可以与机器学习算法相结合，提高计算效率。

参考文献（References）：

[1]Weglein A B. Multiple Attenuation： An Overview of Recent Advances and the Road Ahead[J]. The Leading Edge， 1999， 18 （1）： 40-44.

[2]李鵬，刘伊克，常旭，等.多次波问题的研究进展[J].地球物理学进展，2006，21（3）： 888-897.

Li Peng， Liu Yike， Chang Xu， et al. Progress on the Multiple Problems[J]. Progress in Geophysics， 2006， 21（3）： 888-897.

[3]Robinson E A. Predictive Decomposition of Seismic Traces[J]. Geophysics， 1957， 22（4）： 767-778.

[4]Hampson D. Inverse Velocity Stacking for Multiple Elimination[J]. Canadian Journal of Exploration Geophysicists， 1986， 22（1）： 44-55.

[5]Ryu J V. Decomposition （DECOM） Approach Applied to Wave Field Analysis with Seismic Reflection Records[J]. Geophysics，1982， 47 （6）： 869-883.

[6]胡天跃， 王润秋，White R E. 地震资料处理中的聚束滤波方法[J]. 地球物理学报， 2000， 43（1）： 105-115.

Hu Tianyue， Wang Runqiu， White R E. Method in Seismic Data Processing[J]. Chinese Journal of Geophysics， 2000， 43（1）： 105-115.

[7]Weglein A B， Boyse W E， Anderson J E. Obtaining Three-Dimensional Velocity Information Directly from Reflection Seismic Data： An Inverse Scattering Formalism[J]. Geophysics， 1981， 46（8）： 1116-1120.

[8]Berryhill J R， Kim Y C. Deep-Water Peg Legs and Multiples：Emulation and Suppression[J]. Geophysics， 1986， 51（12）： 2177-2184.

[9]Berkhout A J， Verschuur D J. Estimation of Multiple Scattering by Iterative Inversion： Part I： Theoretical Considerations[J]. Geophysics， 1997， 62（5）： 1586-1595.

[10]王睿，王德利，胡斌，等.基于f-x EMD波場分离的绕射多次波压制方法[J].吉林大学学报（地球科学版），2021，51（2）：597-606.

Wang Rui， Wang Deli， Hu Bin， et al. Diffracted Multiple Elimination Based on f-x EMD Wavefield Separation[J]. Journal of Jilin University （Earth Science Edition）， 2021， 51 （2）：597-606.

[11]Radon J. ber die Bestimmung von Funktionen durch ihre Integralwerte lngs gewisser Mannigfaltigkeiten， Ber[J].Verh Schs Akad， 1917， 69： 262-277.

[12]Sacchi M D， Ulrych T J. High-Resolution Velocity Gather and Offset Space Reconstruction[J]. Geophysics， 1995， 60（4）： 1169-1177.

[13]Herrmann P， Mojesky T， Magesan M， et al.De-aliased， High-Resolution Radon Transforms [C]//SEG 70th Annual International Meeting. Calgary： SGE， 2000： 1953-1956.

[14]熊登， 赵伟， 张剑锋. 混合域高分辨率抛物Radon变换及在衰减多次波中的应用[J]. 地球物理学报， 2009， 52（4）： 1068-1077.

Xiong Deng， Zhao Wei， Zhang Jianfeng.Hybrid-Domain High-Resolution Parabolic Radon Transform and Its Application to Demultiple[J]. Chinese Journal of Geophysics， 2009， 52（4）： 1068-1077.

[15]Li Z N， Li Z C.Multiple Attenuation Using λ-f Domain High-Resolution Radon Transform[J]. Applied Geophysics， 2013， 10（4）： 433-441.

[16]巩向博， 韩立国， 王升超．混合域高分辨率双曲Radon变换及其在多次波压制中的应用[J]. 石油物探， 2016， 55（5）： 711-718.

Gong Xiangbo， Han Liguo， Wang Shengchao. High-Resolution Hyperbolic Radon Transform and Its Application in Multiple Supression[J]. Geoghysical Prospecting for Petroleum，2016， 55（5）： 711-718.

[17]Chen S S， Donoho D L， Saunders M A. Atomic Decomposition by Basis Pursuit[J]. SIAM Review， 2001， 43（1）： 129-159.

[18]Chartrand R， Staneva V. Restricted Isometry Properties and Nonconvex Compressive Sensing[J]. Inverse Problems， 2008， 24（3）： 657-682.

[19]Xu Zongben， Zhang Hai， Wang Yao， et al.L_1/2Regularization[J]. Science China （Information Science）， 2010， 53： 1159-1169.

[20]Zeng Jinshan， Fang Jian， Xu Zongben.Spare SAR Imaging Based on L_1/2Regularization[J]. Science China （Information Science）， 2012， 55（8）： 1755-1775.

[21]Sun Le， Wu Zebin， Xiao Liang， et al. A Novel L_1/2Sparse Regression Method for Hyperspectral Unmixing[J]. International Journal of Remote Sensing， 2013， 34（20）： 6983-7001.

[22]康治梁，张雪冰.基于L_1/2正则化理论的地震稀疏反褶积[J].石油物探， 2019， 58（6）：855-863.

Kang Zhiliang， Zhang Xuebing. Seismic Sparse Deconvolution Based on L_1/2Regularization[J]. Geophysical Prospecting for Petroleum， 2019， 58（6）： 855-863.

[23]高棒棒.基于高分辨率稀疏Radon变换保幅处理方法研究[D]. 西安：西安石油大学， 2021：13-15.

Gao Bangbang. Research on Amplitude Preserving Processing Method Based on High-Resolution Sparse Radon Transform [D]. Xian： Xian Shiyou University， 2021： 13-15.

[24]张军华，吕宁，雷凌，等. 抛物线拉冬变换消除多次波的应用要素分析[J].石油地球物理勘探，2004，39（4）： 398-405.

Zhang Junhua， Lü Ning， Lei Ling， et al. Analysis of Applied Factors for Using Parabolic Radon Transform to Remove Multiple[J]. Oil Geophysical Prospecting， 2004， 39（4）： 398-405.

[25]Yang A Y， Sastry S S， Ganesh A， et al. Fast l₁-Minimization Algorithms and an Application in Robust Face Recognition： A Review[C]//2010 IEEE International Conference on Image Processin. Hong Kong： IEEE， 2010： 1849-1852.

[26]Daubechies I， Defrise M， De Mol C. AnIterative Thresholding Algorithm for Linear Inverse Problems with a Sparsity Constraint[J]. Communications on Pure and Applied Mathematics， 2004， 57（11）： 1413-1457.

[27]Beaton A E， Tukey J W. The Fitting of Power Series， Meaning Polynomials， Illustrated on Band-Spectroscopic Data[J].Technometrics， 1974， 16（2）： 147-185.

[28]Figueiredo M A T， Nowak R D， Wright S J. Gradient Projection for Sparse Reconstruction： Application to Compressed Sensing and Other Inverse Problems[J]. IEEE Journal of Selected Topics in Signal Processing， 2007， 1（4）： 586-597.

[29]Xu Zongben， Chang Xiangyu， Xu Fengmin， et al. L_1/2Regularization： A Thresholding Representation Theory and a Fast Solver[J]. IEEE Transactions on Neural Nwtworks and Learning Systenms， 2012， 23（7）： 1013-1027.

[30]Zuo Wangmeng， Meng Deyu， Zhang Lei， et al.A Generalized Iterated Shrinkage Algorithm for Non-Convex Sparse Coding[C]//2013 IEEE International Conference on Computer Vision. Sydney： IEEE， 2013： 217-224.

[31]李允怡.基于非凸正则化的图像恢复技术研究[D]. 南京：南京邮电大学， 2020： 30-33.

Li Yunyi. Research on Image Recovery Technologyvia Nonconvex Regularization Method [D]. Nanjing： Nanjing University of Posta and Telecommunications， 2020： 30-33.

[32]Beck A， Teboulle M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems[J]. SIAM Journal on Imaging Sciences， 2009， 2（1）： 183-202.

[33]張岩，刘小秋，李杰，等. 基于时频联合深度学习的地震数据重建[J].吉林大学学报（地球科学版），2023， 53（1）：283-296.

Zhang Yan， Liu Xiaoqiu， Li Jie， et al. Seismic Data Reconstruction Based on Joint Time-Frequency Deep Learning[J]. Journal of Jilin University （Earth Science Edition）， 2023， 53（1）： 283-296.