基于系数匹配与参数整合的P波旅行时计算方程

魏建 孙祥娥

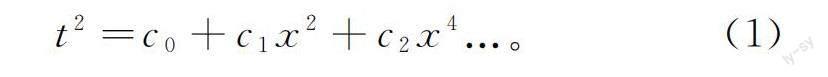
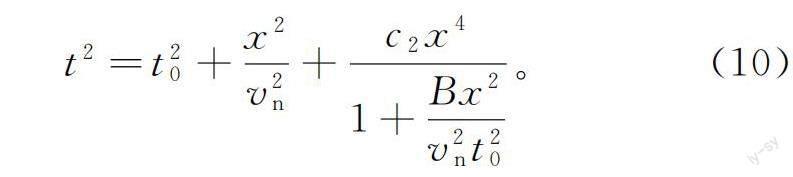
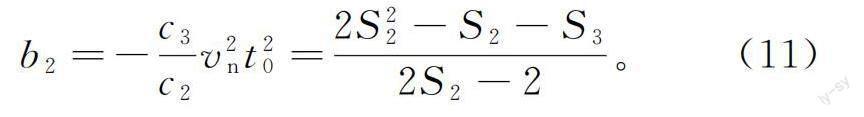
摘要：基于泰勒展开的旅行时公式是计算P波旅行时的一种常用方法。泰勒展开的结果仅在计算点附近准确，而地层中具有垂直对称轴的横向各向同性（transverse isotropy with vertical symmetry axis， VTI）介质进一步放大了旅行时计算的不准确性。本文提出了一种改进的P波旅行时计算方法。该方法以基于泰勒展开的偏移距八阶旅行时方程为基础，利用系数匹配方法分别处理偏移距八阶项与六阶项的系数、偏移距六阶项与四阶项的系数，用整合处理优化得到的参数结构，形成了基于系数匹配与参数整合的偏移距四阶P波旅行时计算方法。水平层状VTI介质模型测试结果表明，该方法能够得到更小的计算误差，保证其在远偏移距处具有较好的表现。三维垂直地震剖面数据实验结果表明，该方法经参数调整后能够进行数据分析，在中偏移距处的表现相对稳定，在远偏移距处具有一定优势。

關键词：旅行时计算；系数匹配；参数整合；VTI介质

doi：10.13278/j.cnki.jjuese.20220309

中图分类号：P631

文献标志码：A

收稿日期：2022-11-10

作者简介：魏建（1991-），男，博士研究生，主要从事油气信息探测与仪器装备方面的研究，E-mail： 201873033@yangtzeu.edu.cn

通信作者：孙祥娥（1970-），女，教授，博士生导师，主要从事地震信号处理方面的研究，E-mail： sxeyangtzeu@163.com

基金项目：国家自然科学基金项目（51978078）

Supported by the National Natural Science Foundation of China （51978078）

P-Wave Traveltime Calculation Equation Based on Coefficient

Matching and Integration ProcessingWei Jian， Sun Xiange

College of Electronic Information， Yangtze University， Jingzhou 434023， Hubei， China

Abstract： The traveltime formula based on Taylor expansion is a common method to calculate P-wave traveltime. The Taylor expansion is accurate only near the calculation point， and the inaccuracy of the traveltime approximation is further magnified in the medium of   transverse isotropy  with vertical  symmetry axis   （VTI）. An improved method for calculating P-wave traveltime is presented in this paper. This method utilizes the 8th-order offset-traveltime equation based on the Taylor expansion， and the coefficient matching method is used to determine the coefficients of the series expansion. Then the integration processing is used to optimize the parameters. Finally， the 4th-order P-wave traveltime calculation method is formed  based on  coefficient matching and parameter integration. The test results for horizontal layered VTI medium models show that the proposed method has relatively small numerical errors and relatively good performance at the far offset. The experimental results for 3D VSP data show that after parameter adjustment， the method effectively analyzes the data， exhibiting stable performance at middle offsets and a certain advantage at far offsets.

Key words： traveltime calculation; coefficient matching; parameter integration; VTI medium

0 引言

旅行时计算公式是地球物理学的重要研究课题之一，其计算精度影响着速度分析、时差校正、成像和正向建模等关键处理步骤^[1]。为了在具有垂直对称轴的横向各向同性（transverse isotropy with vertical symmetry axis， VTI）介质中获得更准确的P波旅行时，P波旅行时方程已由双曲线形式逐渐转变为非双曲线形式。

在非双曲线形式的旅行时公式中，基于泰勒级数展开的P波近似公式是最基本的一种计算方法，如：Castle^[2]通过改进高阶旅行时公式提出的平移双曲线近似法，Alkhalifah等^[3]利用声学近似理论提出的三参数偏移距四阶旅行时计算方法，Ursin等^[4]使用一次系数匹配方法提出的偏移距四阶旅行时计算方法，以及Ursin等^[5]随后提出的改进的几何扩展近似方法。近期，Xu等^[6]提出了基于偏移距泰勒级数展开与声学近似的计算方法。基本的计算方法受限于偏移距高阶项的使用，影响了其在介质中计算的准确性。除了基于泰勒级数展开的基本旅行时计算方法之外，其他能够提高旅行时计算精度的方法相继被提出。Fomel^[7]通过研究相速度与群速度的关系，提出了基于椭圆近似的旅行时计算方法。為了提高扰动方法的准确性，随后提出了优化后的扰动方法^[8-9]。随着研究的深入，Fomel等^[10]提出了基本广义时差近似法，在一定条件下与基于椭圆近似方法具有相同形式。针对基本广义时差方程存在计算参数不对称及准确性不高的情况，提出了通过增加参与计算参数以及射线数目的改进方法，有：修正的广义时差近似法^[11]、扩展的广义时差近似法^[1]、基于三射线的广义时差近似法^[12]以及改进的广义时差近似法^[13]。之后，Ravve等^[14]提出了基于五参数的旅行时计算方法。Abedi^[15]基于有理近似方法提出了多阶旅行时计算方程，随后与Pardo通过计算无限偏移距附近的渐近级数构建了新的旅行时计算方法^[16]。基于旅行时计算相关理论的快速发展，进一步改善旅行时计算准确性的方法将会被提出并广泛应用。

在VTI介质中，一般泰勒级数展开的传统旅行时方程的计算会变得不准确，如何改善这种情况一直是研究的重点。基于此，本文以一般泰勒级数P波旅行时方程为基础，将两次系数匹配方法与参数整合处理相结合，提出了适用于VTI介质的旅行时计算新方法，并通过模型和实际地震数据的测试与分析证明该方法的优势，为旅行时计算研究提供新思路。

1 理论方法

1.1 偏移距四阶旅行时计算公式

基于泰勒级数展开的旅行时与偏移距之间的一般P波近似形式可表示^{[4， 16-17]}为

其中，

式中：t₀为双程旅行时；x为偏移距；v_n为正常时差（normal moveout， NMO）速度；S₂为非均质性参数，与各向异性参数η^[7]的关系为S₂=1+8η。

Ursin等^[4-5]为了提高P波旅行时计算的准确性，根据Alkhalifah等^[3]提出的计算公式，利用方程（1）的偏移距六阶项提出一种偏移距四阶旅行时计算公式^[4]：

其中，

式中，S₃为非均匀性参数。

由于S₃不能直接从地震数据中估计，所以参数S₃与S₂的近似关系可以通过垂直慢度平方公式与声学近似理论^[5]得出：

1.2 基于系数匹配与参数整合处理的旅行时计算方法

在方程（3）的推导过程中，Ursin等^[4-5]利用一次系数匹配法来处理偏移距的六阶项，将方程的最高阶近似为一般的偏移距四次方项。按照这个思路，可以做进一步处理。为了避免推导更为复杂的偏移距系数和非均匀性参数的近似关系，同时不局限于泰勒级数旅行时方程的高阶近似形式，我们以式（3）引入六次方项的处理方式为基础，目前仅将式（1）中偏移距的阶数提高到八次方来尝试提高最终旅行时的计算准确性。若保持偏移距的最高阶数与方程（1）相同，那么系数c₂、c₃和c₄可以利用两次系数匹配方法进行处理。

首先，将方程（1）写为偏移距最高阶为八次方项的截断形式：

其中：

根据方程（3）的形式，在方程（6）的基础上利用一次系数匹配方法来处理系数c₃和c₄，并省略式（6）中偏移距的八阶项，可以得到：

其中，

式中，S₄为非均匀性参数。

在得到式（8）后，按照同样的处理思路能够写出最终的表达式：

式（8）中引入了参数b₁，在一定程度上并不适合直接近似处理式（8）中的偏移距六次方项。基于此，可以继续使用系数匹配方法处理系数c₂和c₃，得到间接参数b₂：

为了优化参数b₁、b₂在旅行时方程应用中的结构，可在式（11）的基础上通过参数整合得到参数B的新形式，即

B=b₁·b^-1₂。    （12）

对于式（12），根据垂直慢度平方公式与声学近似理论^[5]能够得到非均匀性参数S₄与S₂的近似关系：

然后，将式（5）（13）代入到式（9）（11）中，再利用S²₃近似替换S³₂来区别直接简化的形式，即可得到化简后的参数b₁、b₂：

最后，将式（12）（14）带入式（10）中，就能够得到基于两次系数匹配与参数整合（twice coefficient matching and integration， TCMI）的P波旅行时平方公式：

2 实验结果

2.1 模型结果对比

文中使用深度为4 km、偏移距为10 km的水平层状模型（图1），具体参数如表1所示。

误差实验的对比方法为：基于两次系数匹配与参数整合的方法、扰动理论近似方法^[8-9]、扩展的广义时差近似方法^[1]以及三阶有理近似方法^[15]，分别记为TCMI、PT（perturbation theory）、EGMA（extended generalized moveout approximation）、RA（rational approximation）。验证4种方法的评价指标为参数方程^[1]计算出的P波准确时间。

其中：

式中：x（p）为参数方程计算出的偏移距；t（p）为参数方程计算出的P波准确时间；p为射线参数；t_0，i、v_n，i、η_i分别为每层的旅行时、NMO速度与各向异性参数^[16]。计算误差^[16]为

式中，t_x为P波旅行时计算值。

2.1.1 均匀层状VTI介质模型

对于均匀层状VTI介质模型，通过式（18）计算得出的误差曲线如图2所示。在整体偏移距上，PT方法与RA方法的计算误差较大，与PT、RA方法相比，TCMI方法具更小的计算误差。当偏移距为0～8.6 km时，TCMI方法的误差小于EGMA方法；当偏移距为8.6 km时，TCMI方法与EGMA方法的误差曲线趋向重合；当偏移距大于8.7 km时，EGMA方法的误差为4种方法中最小。在远偏移距10 km处：PT、RA、TCMI和EGMA方法的误差分别为2.34%、1.63%、1.33%、0.95%；与PT、RA方法相比，TCMI方法的计算精度分别提高了1.01%、0.30%，相比于EGMA方法，计算精度降低了0.38%。综上可知：在均匀层状各向异性介质中，TCMI方法在偏移距0～8.6 km范围内具有较小的误差，在偏移距8.6～10 km范围内的误差仅小于EGMA方法。

2.1.2 非均匀层状VTI介质模型

非均匀层状VTI介质模型的误差曲线如图3所示。在图3中：TCMI方法与其他3种方法的计算误差相比仍然较小；由于RA方法与PT方法计算误差的差值较为接近，会出现视觉上的重合，实际上PT方法的误差更大。在远偏移距10 km处：PT、RA、EGMA和TCMI方法的误差分别为5.74%、5.73%、5.03%、1.83%；与PT、RA和EGMA方法相比，TCMI方法的准确性分别提高了3.91%、3.90%、3.20%。综上可知：在非均匀VTI介质中，TCMI方法在整体以及远偏移距处均具有更小的计算误差。

2.2 实际地震数据结果对比

VTI介质是一種能够近似表示成具有水平层状的周期性薄互层介质，在实际地震数据中较为常见。实验对比使用的某研究区三维垂直地震剖面（3D vertical seismic profile， 3D VSP）数据同样具有类似性质，其检波器共160级，观测深度为275.84～2 700.00 m。

在实际地震数据验证中，使用孙祥娥等^[18]提出的时差对比方法，即将3D VSP的初至时间作为衡量标准，通过时差判断旅行时公式的表现。时差分析方法如下：

t_d=t_x-t_fb。    （19）

式中：t_d为时差；t_fb为初至时间。

2.2.1 方法适用性

针对实际数据的研究重点，以深度1 784.76 m的实验结果为例，初至时间如图4所示。TCMI方法通过式（19）计算出的时差结果如图5所示。由图5可知：偏移距1 500 m之后的时差并未保持相对水平，而是出现向下弯曲的情况。

基于弯曲情况以及分析TCMI方法的组成，发现：该情况是由整合处理得到的参数B（式（12））造成的。式（12）的提出主要基于两点考虑：一是Ursin等^[4-5]提出的分式结构的思想；二是以模型结果为导向。为了使TCMI方法更好地应用于实际数据，基于以上两点考虑，此时应动态调整参数B的组合形式：

B=b₂·b^-1₁。    （20）

此时，TCMI方法计算出的时差如图6所示。由图6可看出，调整参数后的时差结果相对水平，与图5差异明显;说明调整参数后的TCMI方法能够应用于实际地震数据中。

基于模型与实际数据的结果，此时可将参数B称为动态参数，这为后续将TCMI方法优化为自适应的形式奠定了基础。

2.2.2 方法对比

EGMA、RA、PT方法和调整参数后的TCMI方法通过式（19）计算出的时差对比结果如图7所示。由图7可看出：TCMI方法与经典方法，即EGMA、RA、PT方法，计算出的时差均在一定范围内，说明调整参数后TCMI方法有效。

为了区分TCMI方法与其他3种方法的差别，我们计算了EGMA、RA、PT方法时差与TCMI方法时差的差值，结果如图8所示。分析图8可知：TCMI方法与EGMA、RA、PT方法的时差之差均较小，但在中偏移距500～2 500 m范围内，因TCMI方法具有较大的时差计算值，所以EGMA、RA、PT方法与TCMI方法时差差值曲线会出现小于0的情况；而在远偏移距，即大于2 500 m时，TCMI方法的计算值较小，可知该方法在该范围具有优势。对于其他3种方法，在中偏移距范围内，EGMA方法与RA方法的差值较小，均与PT方法的差值较大；在远偏移距范围内，EGMA方法的优势大于RA和PT方法，PT方法的表现一般。

3 討论

本文在利用含有八次方项的旅行时公式推导出一种新的旅行时计算方法。在此基础上，还可以将偏移距的阶数提高多少是需要思考的^[17]，是否仍能使用类似的处理方法也是需要着重研究的。在计算P波旅行时的时候，还可以通过计算模型空间中每一点的到时来分析每一点到时的误差分布。在实际数据的实验中，我们提出了与模型试验中形式不同的参数B。这两种形式使得TCMI方法更加丰富且完善，为后续将其优化为自适应的计算方法奠定了基础。另外，与射线追踪方法相比，旅行时公式仍存在一定不足，所以，研究旅行时公式应集中在它的应用上，如相关参数的反演^[19]或成像^[20-22]。使用哪种公式进行分析需要重点分析，对于TCMI方法，还可以尝试联合其他旅行时公式同时对数据进行分析，这是一个可以深入研究的方向。

4 结论

该研究基于一般的偏移距八阶旅行时计算公式，利用系数匹配方法得到了处理高阶项后的参数b₁、b₂，然后利用参数整合、垂直慢度与声学近似理论，结合实际地震数据实验得到了参数B的两种形式，形成了基于两次系数匹配与参数整合的P波旅行时计算方法，得到以下结论：

1）对于各向异性参数相同的层状VTI介质，与扩展的广义时差近似方法、三阶有理近似方法相比，基于两次系数匹配与参数整合的P波旅行时计算方法在远偏移距10 km处的计算精度分别提高了1.01%、0.30%；相比于扩展的广义时差近似方法，计算精度降低了0.38%。对于各向异性参数不同的VTI介质，与扩展的广义时差近似方法、三阶有理近似方法和扩展的广义时差近似方法相比，准确性分别提高了3.91%、3.90%、3.20%。

2）对于3D VSP数据，通过调整参数B的形式，使基于两次系数匹配与参数整合的P波旅行时计算方法适用于实际数据分析。通过实验对比，基于两次系数匹配与参数整合的P波旅行时计算方法在远偏移距范围内具有一定优势。

3）基于两次系数匹配与参数整合的P波旅行时计算方法在模型与实际数据实验中的表现说明，系数匹配与参数整合处理可以在提高旅行时计算准确性上起到重要作用，但在一定程度上也会影响方法的计算稳定性。

4）结合模型与实际数据实验中的表现可知：基于两次系数匹配与参数整合的P波旅行时计算方法可以成为分析旅行时的一种选择。如何提高该方法的稳定性，以及将参数B的两种形式更好地与方法结合中是下一步的研究重点。

参考文献（References）：

[1]Abedi M M， Stovas A. Extended Generalized Nonhyperbolic Moveout Approximation [J]. Geophysical Journal International，2019，26（2）：1428-1440.

[2]Castle R J. A Theory of Normal Moveout[J]. Geophysics， 1994， 34（6）： 859-881.

[3]Alkhalifah T， Tsvankin I. Velocity Analysis for Transversely Isotropic Media [J]. Geophysics，1995，60（5）：1550-1566.

[4]Ursin B， Stovas A. Traveltime Approximations for a Layered Transversely Isotropic Medium[J]. Geophysics， 2006， 71（2）： D23-D33.

[5]Ursin B， Stovas A. Improved Geometrical Spreading Approximation in Layered Transversely Isotropic Media [J]. Geophysics， 2009， 74（5）： D85-D95.

[6]Xu S， Stovas A， Mikada H. Traveltime and Relative Geometric Spreading Approximation in Elastic Orthorhombic Medium [J]. Geophysical Journal International， 2020， 85（5）： C153-C162.

[7]Fomel S. On Anelliptic Approximations for qP Velocities in VTI Media [J]. Geophysics， 2004， 52（3）： 247-259.

[8]Xu S， Stovas A， Hao Q. Perturbation-Based Moveout Approximations in Anisotropic Media[J]. Geophysical Prospecting， 2017， 65（5）： 1218-1230.

[9]Abesdi M M， Riahi M A， Stovas A. Three-Parameter NMO Correction in Layered Anisotropic Media： A Stretch-Free Approach [J]. Geophysics， 2019， 84（3）： C129-C142.

[10]Fomel S， Stovas S A. The Generalized Non-Hyperbolic Moveout Approximation [J]. Geophysics， 2010， 75（2）： U9-U18.

[11]Stovas A， Fomel S. The Modified Generalized Moveout Approximation： A New Parameter Selection [J]. Geophysics， 2017， 65（3）： 687-695.

[12]Abedi M M， Riahi M A， Stovas A. A New Parameterization for Generalized Moveout Approximation Based on Three Rays [J]. Geophysical Prospecting， 2019， 67（5）： 1243-1255.

[13]Jin S， Stovas A， Hu X. Improved Generalized Moveout Approximation with a Novel Parameterization [J]. Geophysics， 2022， 87（3）： C49-C61.

[14]Ravve I， Koren Z. Traveltime Approximation in Vertical Transversely Isotropic Layered Media [J]. Geophysical Prospecting， 2017， 65（6）：1559-1581.

[15]Abedi M M. Rational Approximation of P-Wave Kinematics： Part 1： Transversely Isotropic Media [J]. Geophysics， 2020， 85（5）： C175-C185.

[16]Abedi M M， Pardo D. Large-Offset P-Wave Traveltime in Layered Transversely Isotropic Media [J]. Geophysics， 2021， 86（3）： C65-C74.

[17]魏建，孙祥娥. VTI介質中基于降阶补偿处理的旅行时计算方法[J]. 山东科技大学学报（自然科学版），2022，41（1）：86-91.

Wei Jian， Sun Xiange. A Method of Traveltime Calculation Based on Descending Order Compensation Processing in VTI Medium[J]. Journal of Shandong University of Science and Technology （Natural Science）， 2022， 41（1）： 86-91.

[18]孙祥娥，凌云，高军，等. 各向异性假设条件下三维 VSP 与地面地震数据旅行时差分析及参数求取[J]. 石油地球物理勘探，2009，44（6）：720-725.

Sun Xiange， Ling Yun， Gao Jun， et al. Travel Time-Difference Analysis and Parameter Extraction for 3D VSP Data and Surface Seismic Data in Anisotropic Media [J]. Oil Geophysical Prospecting， 2009， 44（6）： 720-725.

[19]张利振，孙成禹，王志农，等. 面波信息约束的初至波走时层析反演方法[J]. 物探与化探，2023，47（5）：1198-1205.

Zhang Lizhen， Sun Chengyu， Wang Zhinong， et al. First Arrival Wave Travel Time based Tomography Inversion with Surface Wave Information as Constraints[J]. Geophysical and Geochemical Exploration， 2023， 47（5）：1198-1205.

[20]张志鹏，孙章庆，韩复兴，等. 影响高斯束偏移成像质量和效率的主要因素分析[J]. 世界地质，2022，41（2）：349-364.

Zhang Zhipeng， Sun Zhangqiang， Han Fuxing， et al. Analysis of Main Factors Affecting Imaging Quality and Efficiency of Gaussian Beam Migration[J]. World Geology， 2022， 41（2）： 349-364.

[21]李洪丽，刘财，田有，等. 中国东北地壳结构的地震层析成像[J]. 吉林大学学报（地球科学版），2022，52（1）：270-280.

Li Hongli， Liu Cai， Tian You， et al. Seismic Tomography of the Crustal Structure in Northeast China[J]. Journal of Jilin University （Earth Science Edition）， 2022， 52（1）： 270-280.

[22]万晓杰，巩向博，成桥，等. 基于DeCNN的逆时偏移低频噪声压制方法[J].吉林大学学报（地球科学版），2023，53（5）：1593-1601.

Wan Xiaojie， Gong Xiangbo， Cheng Qiao， et al. Eliminating Low-Frequency Noise in Reverse-Time Migration Based on DACNN[J]. Journal of Jilin University （Earth Science Edition）， 2023， 53（5）： 1593-1601.