基于分数阶理论的软泥岩一维次固结蠕变模型
2024-02-27任思远倪万魁陈军廷拓文鑫杨珍珍
任思远 倪万魁 陈军廷 拓文鑫 杨珍珍
摘要:工程中因岩石蠕变而诱发的灾害屡见不鲜,其中的软岩蠕变在实际工程中也较为常见。为探讨软岩蠕变特性,并准确预测软岩蠕变变形,本研究首先对宁夏固原市隆德县的软泥岩进行了一维次固结蠕变试验,分析了一维次固结蠕变试验下软泥岩的蠕变特性;然后引入了分数阶理论的概念,推演能够描述非线性蠕变特征的分数阶Burgers模型本构方程;最后利用Matlab中lsqcurvefit算法对软泥岩一维次固结蠕变试验数据进行数值求解,分析了分数阶阶数对软泥岩一维次固结蠕变曲线的影响。蠕变试验表明:软泥岩蠕变机制符合固結蠕变中瞬时变形、固结变形、稳定变形三阶段,并呈明显的非线性特征,且原状、重塑试样在固结过程中均产生了较大程度的次固结蠕变,最大变形量可占总变形量的59%。数值模拟结果表明:分数阶Burgers模型能够更好地描述次固结蠕变的非线性特征;模型分数阶阶数γ有较强的敏感性,能够反映拟合曲线的弹性阶段及之后的非线性黏弹性阶段,而分数阶阶数β敏感性较差,仅能对黏弹性阶段的蠕变趋势做出细微反应。
关键词:软泥岩;分数阶理论;岩石蠕变;Burgers模型;宁夏固原市
doi:10.13278/j.cnki.jjuese.20220119
中图分类号:TU458
文献标志码:A
收稿日期:2022-04-19
作者简介:任思远(1998-),男,硕士研究生,主要从事岩土蠕变特性方面的研究,E-mail:1073429405@qq.com
通信作者:倪万魁(1965-),男,教授,博士生导师,主要从事岩土力学与工程方面的研究,E-mail: niwankui@chd.edu.cn
基金项目:国家自然科学基金项目(41931285)
Supported by the National Natural Science Foundation of China (41931285)
One-Dimensional Secondary Consolidation Creep Constitutive Model
of Soft Mudstone Based on Fractional Order TheoryRen Siyuan,Ni Wankui,Chen Junting,Tuo Wenxin,Yang Zhenzhen
Geology Engineering and Geomatics College,Changan University,Xian 710054,China
Abstract: Disasters induced by rock creep in engineering are common, and soft rock creep is also more common in actual engineering. In order to explore the soft rock creep characteristics and accurately predict the soft rock creep deformation. In this study, firstly, a one-dimensional secondary consolidation creep test was carried out on the soft mudstone in Lund area of Guyuan City, Ningxia, and the creep characteristics of soft mudstone under the one-dimensional secondary consolidation creep test were analyzed. Secondly, the concept of fractional order theory was introduced to derive the fractional order Burgers model constitutive equation which can describe the nonlinear creep characteristics. Finally, the lsqcurvefit algorithm in Matlab was used to numerically solve the one-dimensional secondary consolidation creep test data of soft mudstone, and the effect of fractional order number on the one-dimensional secondary consolidation creep curve of soft mudstone was analyzed. One-dimensional secondary consolidation creep test shows that the creep mechanism of soft mudstone conforms to the three stages of transient deformation, consolidation deformation, and stable deformation in consolidation creep, and shows obvious nonlinear characteristics. And the undisturbed sample, remodeled sample in the consolidation process produced a large degree of secondary consolidation creep, the maximum deformation can account for 59% of the total deformation. Numerical simulation results show that the fractional order Burgers model can better describe the nonlinear characteristics of the sub-consolidation creep; Model fractional order γ has a strong sensitivity to reflect the elasticity of the fitted curve and the nonlinear viscoelasticity after the stage, and fractional order β sensitivity is poorer than the viscoelasticity stage of the creep tendency to make a subtle response.
Key words: soft mudstone;fractional order theory;rock creep;Burgers model;Guyuan City,Ningxia
0 引言
岩石蠕变是指在恒定应力下岩石变形随着时间增长的现象。在工程中,因岩石蠕变累计而诱发的地质灾害屡见不鲜[1-3]。其中,软岩的蠕变特性相比与普通岩石更加明显,在实际工程中也更为常见[4]。因此,选择一个可以准确描述软岩蠕变特性的模型十分重要。
在长期的研究中,学者们常采用经验模型、元件模型、半经验半理论模型等方法来研究岩石蠕变曲线特征[5-10]。如:杨春和等[5]考虑了不同力学特性岩层间的细观位移协调,建立了细观弯曲效应的Cosserat截至扩展本构模型;王军保等[6]对稳态蠕变拐点法进行改进,得到了描述岩石长期强度的经验公式,并采用反S函数求解法,提出了一种描述盐岩单轴压缩条件下的蠕变经验公式;年廷凯等[7]基于固结理论分析了粉砂土的一维次固结蠕变行为,利用Kelvin模型与Burgers模型描述了粉砂土的固结蠕变特性;李银平等[8]从细观力学的角度分析,综合考虑多介质弹性、蠕变特性和介质体积分数,建立了宏观Cosserat蠕变本构模型;范翔宇等[9]为探讨煤岩钻井壁的蠕变失稳规律,将Bingham模型与Bonaitin Thomson模型结合,获得了符合储气层煤岩蠕变规律的模型;朱杰兵等[10]从材料损伤角度出发,探究岩石流变力学参数与黏性应变的负指数关系,建立了变参非线性整数阶Burgers模型。由此可见,为了较好地描述软岩的蠕变特征,研究者通常会采用多模型组合以及引入材料非线性参数的方式,不过这种蠕变模型建立方式会增加模型的复杂程度或者受材料参数的制约。产生上述问题的主要原因是整数阶模型无法准确地描述岩石蠕变中非线性阶段的特征[11]。
为此,诸多学者逐渐对分数阶理论下的非线性元件组合模型开展了研究。如:殷德顺等[12]通过分数阶理论推导引入了一种能够很好反映非线性应力松弛和蠕变现象的软体元件,并探究了软体元件与其他传统元件组合所产生的蠕变效果;罗庆姿等[13-15]将两种分数阶理论下的黏壶元件引入Nishihara模型并对模型进行推演验证,建立了新的分数阶黏弹塑性蠕变本构模型;康永刚等[16]将Burgers模型中串联黏壶元件改进为定常数元件,将并联黏壶元件改進为分数阶元件来描述蠕变加速阶段;李祖勇等[17]采用核磁共振技术检测砂岩解冻过程中空隙含水量的变化,并结合基于分数阶理论的蠕变本构方程,讨论了解冻过程中的砂岩蠕变特性。然而,已开展的多数研究仅证明了分数阶理论对岩土试验具有很高的适用性,并未讨论分数阶模型中参数的敏感性。
有鉴于此,本文先通过对宁夏固原市隆德县软泥岩进行一维次固结蠕变试验,分析该软泥岩的蠕变特性;然后将传统Burgers模型中的黏性元件替换成分数阶元件,推演了分数阶理论下的Burgers模型;最后利用Matlab中lsqcurvefit算法对软泥岩一维次固结蠕变实验数据进行数值求解。本文旨在探查宁夏软泥岩蠕变特性,建立适用于软泥岩的分数阶蠕变模型,以及探究模型中参数敏感特性。
1 软泥岩蠕变实验
1.1 试验材料及实验方法
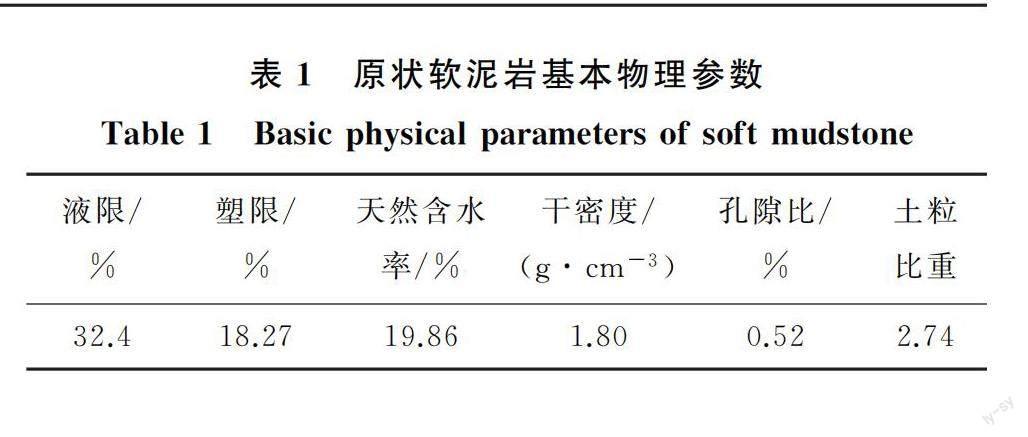
试验所用样品为取自宁夏固原市隆德县的红色软泥岩,基本物理参数见表1。由于软泥岩物理力学性质接近于土体,因此一维次固结试验参照《土工试验方法标准》(GB/T 50123—2019)[18]进行。试样分为原状样和重塑样两类:原状样是由软泥岩岩心削制而成,试样含水率ω为20%;重塑样是由软泥岩经过风干、碾碎、过筛后压制而成。重塑样干密度与原状样保持一致,试样含水率ω分别设定为18%、20%、22%。制样完成后,试样需在保湿缸中静置48 h。一维次固结蠕变试验采用南京土壤仪器厂WG型高压固结仪进行,试验温度控制在室温25 ℃左右。一维次固结蠕变试验采用分级加载的方式,以加荷比为1的加载序列[19-20]进行加载,具体加载压力分别为100,200,400,800,1 600 kPa。试验过程中土样24 h的变形量不超过0.02 mm时,认为蠕变稳定。
1.2 软泥岩蠕变特性
试验数据采用分别加载的形式表示,得到不同含水率下软泥岩的应变-时间曲线簇如图1所示,可见软泥岩样在第一级荷载100 kPa时产生的变形量普遍大于之后的4级荷载(200、400、800、1 600 kPa)所产生的变形量。这是因为试验采用陈氏加载法,随着荷载的逐渐增加,软泥岩逐渐压密,弹性模量逐渐增大,使得每一级荷载所对应的试样状态不同。此外,由图1还可发现,第一级荷载压缩过程中试样经过固结阶段但曲线仍有一段短暂的加速变化,这是试样在小荷载、短时间作用下颗粒未定向排列,随着时间变化软泥岩缓慢蠕变,颗粒达到定向排列所产生的短暂加速变化[21]。
图2为原状试样在100 kPa下试验数据的应变速率-应变曲线。从图2明显看出,应变速率随着应变增加呈减小趋势,可以将曲线大致分成3个阶段:1)荷载的触变作用产生的大应变速率阶段,即瞬时变形阶段Ⅰ;2)由孔隙水压消散速率主要控制的应变速率减速阶段,即固结变形阶段Ⅱ;3)孔隙水压消散一段时间后由土骨架蠕变主要控制的应变速率稳定阶段,即稳定变形阶段Ⅲ。且应变速率-应变拐点法是一种常用的主次固结划分方法[22],将图2中灰色部分局部放大进行如下分析:首先绘制阶段Ⅱ末端斜线部分切线AB,再绘制阶段Ⅲ近水平曲线切线CD,二者交于O点,O点对应应变的时间便是主次固结分界点。图2中O点对应的应变为0.73%,对应应变速率为0.1×10-4min-1,即主次固结分界点为730 min。
软泥岩各级荷载下的应变速率-应变曲线见图3。由图3可明显发现曲线符合以上提到的瞬时变形、固结变形、稳定变形三阶段,但各级荷载对应曲线有交叉重叠现象。这可能是试验过程中试样结构性发生破坏而导致[23-24]。对于同一个试样,应变速率主要由密实度和压力决定。试验初期,低压力不足以破坏试样的结构强度,因此密实度为影响试样应变速率的主要因素;此时宏观表现为试样随着应力的增加逐渐密实,应变速率也逐渐减小。当压力超过试样的结构强度后,试样内部结构破坏,产生较大变形,此阶段压力作为主要因素影响试样的应变速率;此时宏观表现为试样的应变速率随着压力的增加而增加。而随着压力的持续增加,试样内部孔隙持续被压缩,应变潜力也在减小;此时宏观表现为应变速率逐渐减小,最终趋于0。因此,不同试样应变速率-应变曲线并未表现出单调性的规律,而是出现交叉重叠现象。
根据应变速率-应变拐点主次固结划分法及其分析法对图3a原状样进行分析。观察图3a中局部放大图,可知主次固结分界点对应应变为0.4%~1.0%,应变速率为0.02×10-4~0.10×10-4min-1,即软泥岩原状样主次固结分界点范围为750~1 700 min,再对照图1应变-时间曲线可知,原状样主固结所产生的应变占总应变的41%~64%,次固结所产生的应变占总应变的36%~59%。同理依次分析不同含水率软泥岩重塑样应变速率-应变曲线图3b—d可得,含水率18%重塑泥岩样获得次固结所产生应变为30%~49%,含水率20%重塑泥岩样获得次固結所产生应变为18%~50%,含水率22%重塑泥岩样获得次固结所产生应变为32%~49%。可见次固结蠕变所产生的应变在压缩总应变中占比很大。
2 分数阶本构模型
对于一维次固结所呈现出的衰减和稳态阶段,通常学者通过研究Burgers蠕变模型[25-28]来对其描述。但是有研究[13]表明,这种传统模型属于整数阶的元件模型,拟合曲线不能很好地与实验数据吻合。对此引入非线性的分数阶元件进行改进,以更好地描述实验数据的规律。
2.1 分数阶下的黏壶元件
与经典模型相比,分数阶理论下的模型是将其中的Newton黏壶替换为能用分数阶理论计算的Abel黏壶模型[12]。图4为Abel黏壶的元件构成,对于这种介于纯弹性体和牛顿流体之间的本构关系,可以假设服从改写后的胡克定律σ(t)-dβ0ε(t)/dtβ0[14]。式中:σ为应力;t为时间;ε为应变;β0为分数阶求导阶数,0≤β0≤1。
根据Riemann-Liouville (R-L)分数阶导数[29]定义可得:
式中:Dβ0t为R-L分数阶算子;f(t)为被积函数;m为积分变量;*为Stieltjes卷积;Iβ0(t)为Abel核,Iβ0(t)=(Γ(1-β0)tβ0)-1;Γ为Gamma函数。
采用Koeller[30]提出的应力应变关系,Abel黏壶可以利用式(1)成比例表示:
式中,τ=η/E,η为黏滞性系数。当β0=1时,符合牛顿黏性流体的本构关系;当β0=0时,符合弹性固体的本构关系。
2.2 分数阶模型推导
本文建立的模型由Maxwell体和Kelvin两部分串联而成,如图5所示。其中,含Abel黏壶的分数阶Maxwell体表征瞬态应变及固结蠕变特征,含Abel黏壶的分数阶Kelvin体用以表征稳态蠕变特征,因此总体蠕变趋势可以采用分数阶Burgers模型的形式。
2.3 模型拟合分析
对模型进行拟合分析时,应对模型中各参数进行数值求解。本文选用的拟合算法为Matlab自带的lsqcurvefit算法。该算法集成了最小二乘法中经典的高斯牛顿算法(Guass-Newton)和列文伯格-马夸尔特算法(Levenberg-Marquardt),算法兼具牛顿法及梯度法的特点,对数据拟合更精确快速[33]。
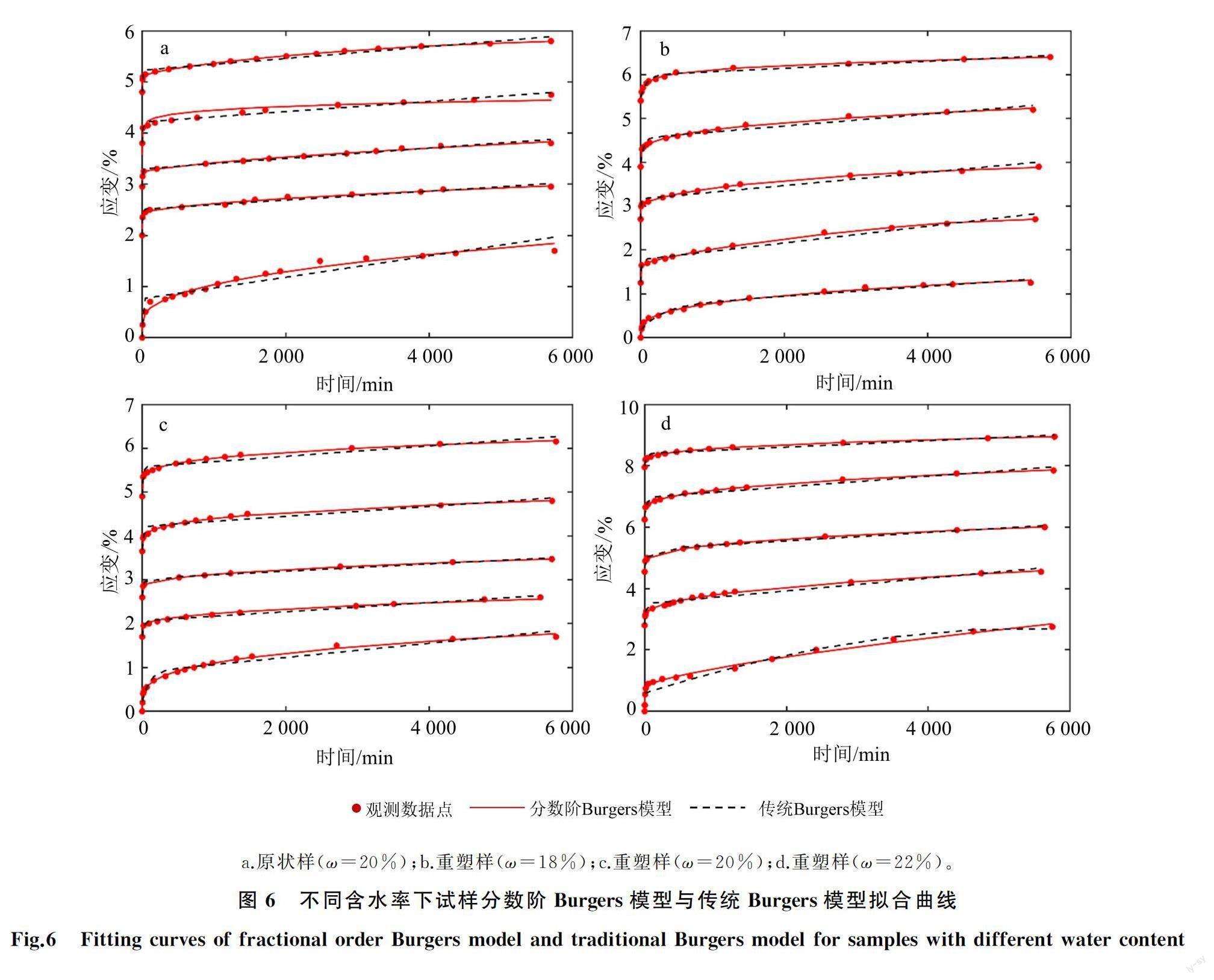
利用Matlab调用2.2小节推演的分数阶Burgers模型(式(18))拟合上述试验数据,验证本文模型在一维次固结蠕变试验中的适用性,并和传统Burgers模型(式(19))的拟合结果进行对比。图6为软泥岩原状样及不同含水率重塑样对两种模型的拟合曲线,可发现分数阶导数的Burgers模型及传统Burgers模型均可以对一维次固结蠕变数据进行拟合,但分数阶导数的Burgers模型以非线性的方式更为精确地描绘出了数据在拐点及之后的变化趋势,而传统的Burgers模型以线性的形式描述蠕变全阶段是不够精确的。且观察100 kPa下的拟合数据,可以明显发现传统模型在稳定蠕变阶段的线性表达使得预测值与实际值相差越来越大。
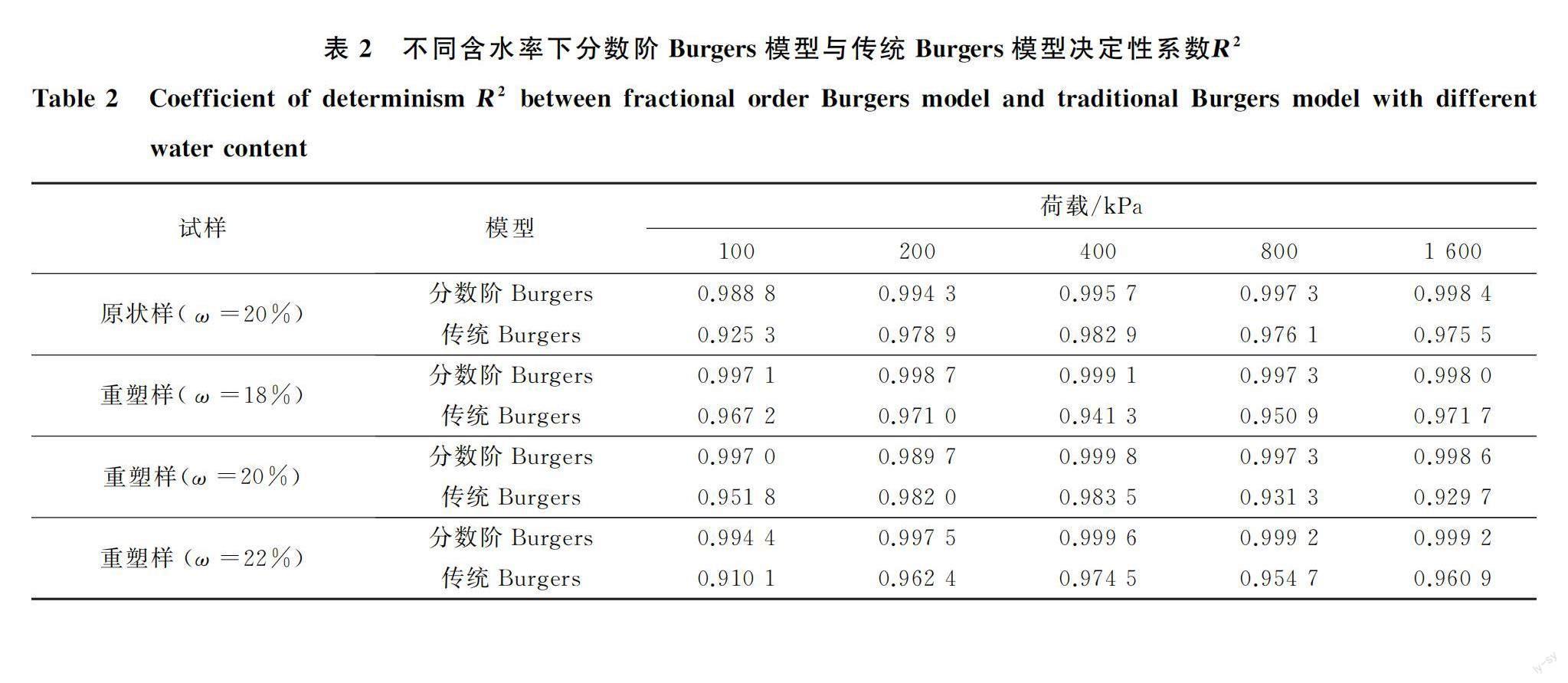
采用 Matlab软件对蠕变本构模型与数据进行拟合优度分析。利用决定性系数R2表达各模型与数据的拟合程度,如表2所示。可以发现传统Burgers模型对一维次固结试验数据的拟合程度分布在0.910 1~0.983 5,而分数阶Burgers模型对该数据的拟合程度普遍在0.995 0左右。拟合参数见表3、表4。
2.4 模型参数敏感性分析
根据表3拟合结果,选取含水率20%、荷载100 kPa下的拟合参数带入式(18),改变分数阶阶数γ,可得到不同阶数γ对应的蠕变曲线(图7)。
分析图7可以发现,随着分数阶模型中阶数γ越大,拟合曲线对应时间为0的应变越小,即弹性变形越小,拐点部位弧度逐渐变缓,且稳态蠕变趋势会产生明显的改变。具体表现为:分数阶阶数γ为0.8时,拐点对应应变约0.2%,经过6 000 min后,曲线最终应变约为0.4%;γ为0.2时,拐点对应应变约1.5%,经过6 000 min后,曲线最终应变约为2.4%。
同时,考虑分数阶Burgers模型中阶数β对蠕变曲线特征的影响,绘制不同分数阶阶数β对应的蠕变应变与时间关系曲线如图8。由图8可知,随着分数阶阶数β逐渐增大,拟合曲线弧度虽然有些许增大,但总体的蠕变趋势保持一致。
从图7、图8可进一步分析分数阶阶数γ、β在拟合过程中对蠕变曲线的影响:分数阶阶数γ为0.8时蠕变应变最小,分数阶阶数至0.2时应变有明显增大,增加幅度近5倍;而分数阶阶数β由0.2增大至0.8过程中应变变化微小,增加幅度仅3%,与γ相比,阶数β敏感性明显较弱。这表明分数阶Burgers模型中分数阶阶数γ能够表达泥岩蠕变曲线全过程;而分数阶阶数β产生的表达能力则略显不足。究其原因,这可能是分数阶Burgers模型中Kelvin体的Abel元件与弹性元件并联,应变受到元件控制,无法如模型中Maxwell体般能在较短时间内发挥作用。即便如此,能产生小应变范围的分数阶阶数β仍在模型拟合过程中发挥着对稳态蠕变阶段校准的作用。
3 結论与建议
1)宁夏固原市隆德县软泥岩蠕变为典型的固结蠕变三阶段,并呈明显非线性特征。通过次固结蠕变试验分析得出,软泥岩原状样蠕变应变占在压缩总应变36%~59%,重塑样蠕变应变占在压缩总应变18%~50%,蠕变应变在压缩总应变中占比较大。
2)经验证,引入分数阶理论构造的分数阶Burgers本构模型相较传统Burgers模型更能体现出软泥岩一维次固结过程中的非线性阶段,拟合精度更高,决定性系数达到0.995 0。
3)对改进后的分数阶Burgers本构模型进行参数影响及敏感性分析,发现分数阶阶数γ有较强的敏感性且能够反映拟合曲线的弹性、非线性黏弹性特征,而分数阶阶数β敏感性较差,仅能对曲线拐点之后的蠕变趋势做出细微反应。
4)虽然分数阶Burgers模型拟合精度高于传统Burgers模型,但由于其模型参数多、公式复杂,影响了实际工程应用价值。后续应对模型简化、参数定量化进行更深入的研究。
参考文献(References):
[1]蔡美峰. 岩石力学与工程[M]. 北京:科学出版社, 2002.
Cai Meifeng. Rock Mechanics and Engineering[M]. Beijing: Science Press, 2002.
[2]赵越,李磊,闫晗,等. 水化-冻融耦合作用下大理岩单轴蠕变力学特性[J]. 吉林大学学报(地球科学版),2023,53(4):1195-1203.
Zhao Yue, Li Lei, Yan Han, et al. Uniaxial Creep Mechanical Properties of Marble Under Hydration Freeze-Thaw Coupling[J]. Journal of Jilin University (Earth Science Edition), 2023, 53 (4):1195-1203.
[3]柴少波,宋浪,周炜,等.水岩作用对充填节理岩石劣化的影响[J].吉林大学学报(地球科学版), 2023, 53(5):1510-1520.
Chai Shaobo, Song Lang, Zhou Wei, et al. Effect of Water-Rock Interactions on the Deterioration of Filled Jointed Rock[J]. Journal of Jilin University (Earth Science Edition), 2023,53(5):1510-1520.
[4]赵建磊,王涛,梁昌玉,等.基于风化红层泥岩蠕变特性的滑坡时效变形分析:以天水雒堡村滑坡为例[J].中国地质灾害与防治学报,2023,34(1):30-39.
Zhao Jianlei, Wang Tao, Liang Changyu, et al.Analysis on Time-Dependent Deformation of Landslide Based on Creep Characteristics of Weathered Red Mudstone: A Case Study of the Luobao Landslide in Tianshui of Gansu Province[J]. The Chinese Journal of Geological Hazard and Control,2023,34(1):30-39.
[5]杨春和,李银平. 互层盐岩体的Cosserat介质扩展本构模型[J]. 岩石力学与工程学报, 2005, 24(23): 4226-4232.
Yang Chunhe,Li Yinping. Expanded Cosserat Medium Constitutive Model for Laminated Salt Rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(23): 4226-4232.
[6]王军保,刘新荣,宋战平,等. 基于反S函数的盐岩单轴压缩全过程蠕变模型[J]. 岩石力学与工程学报, 2018, 37(11): 2446-2459.
Wang Junbao, Liu Xinrong, Song Zhanping, et al. A Whole Process Creeping Model of Salt Rock Under Uniaxial Compression Based on Inverse S Function[J].Chinese Journal of Rock Mechanics and Engineering, 2018, 37(11): 2446-2459.
[7]年廷凯,余鹏程,柳楚楠,等.吹填粉砂土固结蠕变试验及模型[J].吉林大学学报(地球科学版),2014,44(3):918-924.
Nian Tingkai, Yu Pengcheng, Liu Chunan, et al. Consolidation Creep Test and Creep Model of Dredger Fill Silty Sand[J]. Journal of Jilin University( Earth Science Edition),2014,44(3):918-924.
[8]李银平,杨春和. 层状盐岩体的三维Cosserat介质扩展本构模型[J]. 岩土力学, 2006, 27(4): 509-513.
Li Yinping, Yang Chunhe. Three-Dimensional Expanded Cosserat Medium Constitutivemodel for Laminated Salt Rock[J]. Rock and Soil Mechanics, 2006, 27(4): 509-513.
[9]范翔宇,张千贵,艾巍,等. 煤岩储气层岩石蠕变特性与本构模型研究[J]. 岩石力学与工程学报, 2013, 32(2): 3732-3739.
Fan Xiangyu, Zhang Qiangui, Ai Wei, et al. Study on Rock Creep Characteristics and Constitutive Model of Coal Rock Gas Reservoir[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(2): 3732-3739.
[10]朱杰兵,汪斌,邬爱清. 锦屏水电站绿砂岩三轴卸荷流变试验及非线性损伤蠕变本构模型研究[J]. 岩石力学与工程学报, 2010, 29(3): 528-534.
Zhu Jiebing, Wang Bin, Wu Aiqing. Study of Unloading Triaxial Rheological Tests and Its Nonlinear Damage Constitutive Model of Jinping Hydropow Station Green Sandstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 528-534.
[11]Cao P, Youdao W, Yixian W, et al. Study on Nonlinear Damage Creep Constitutive Model for High-Stress Soft Rock[J]. Environmental Earth Sciences, 2016, 75(10): 1-8.
[12]殷德順,任俊娟,和成亮,等. 一种新的岩土流变模型元件[J]. 岩石力学与工程学报, 2007, 26(9): 1899-1903.
Yin Deshun, Ren Junjuan, He Chengliang, et al. A New Geotechnical Rheological Model Element[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(9): 1899-1903.
[13]罗庆姿,陈晓平,王盛,等. 软黏土变形时效性的试验及经验模型研究[J]. 岩土力学, 2016, 37(1): 66-75.
Luo Qingzi, Chen Xiaoping, Wang Sheng, et al. An Experimental Study of Time-Dependent Deformation Behaviour of Soft Soil and Its Empirical Model[J].Rock and Soil Mechanics, 2016, 37(1): 66-75.
[14]吴斐,谢和平,刘建锋,等. 分数阶黏弹塑性蠕变模型试验研究[J]. 岩石力学与工程学报, 2014, 33(5): 964-970.
Wu Fei, Xie Heping, Liu Jianfeng, et al. Experimental Study of Fractuional Viscoelastic-Plastic Creep Model[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(5): 964-970.
[15]Wu F, Chen J, Zou Q L. A Nonlinear Creep Damage Model for Salt Rock[J]. International Journal of Damage Mechanics, 2019, 28(5): 758-771.
[16]康永剛,张秀娥. 岩石蠕变的非定常分数伯格斯模型[J]. 岩土力学, 2011, 32(11): 3237-3241.
Kang Yonggang, Zhang Xiue. Nonstationary Parameter Fractional Burgers Model of Rock Creep[J]. Rock and Soil Mechanics, 2011, 32(11): 3237-3241.
[17]李祖勇,杨更社,魏尧. 白垩系冻结砂岩解冻过程中蠕变力学特性研究[J]. 岩石力学与工程学报, 2021, 40(9): 1777-1788.
Li Zuyong, Yang Gengshe, Wei Yao. Study on Creep Mechanical Properties of Frozen Cretaceous Sandstone During Thawing Process[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(9): 1777-1788.
[18]土工试验方法标准:GB/T 50123—2019[S].北京:中国计划出版社,2019.
Standard for Geotechnical Testing Method:GB/T 50123—2019[S]. Beijing: China Planning Press, 2019.
[19]谭儒蛟,焦宇杰,徐文杰. 天津滨海软土固结-蠕变特性及微观结构分析[J]. 工程勘察, 2015, 43(5): 14-17.
Tan Rujiao, Jiao Yujie, Xu Wenjie. Study on the Consolidation-Creep Characteristics and Microstructure of the Soft Soil in Tianjin Binhai Area[J]. Geotechnical Investigation & Surveying, 2015, 43(5): 14-17.
[20]韩伶敏,徐燕,高康. 季冻区草炭土固结特性研究[J]. 水文地质工程地质,2022,49(4): 109-116.
Han Lingmin, Xu Yan, Gao Kang. Consolidation Characteristics of the Turfy Soil in Seasonally Frozen Area[J]. Hydrogeology & Engineering Geology, 2022, 49(4): 109-116.
[21]陈晓平,周秋娟,朱鸿鹄,等. 软土蠕变固结特性研究[J]. 岩土力学, 2007, 28(1): 1-10.
Chen Xiaoping, Zhou Qiujuan, Zhu Honghu, et al. Researchon Creep and Consolidation Characteristics of Soft Soil[J]. Rock and Soil Mechanics, 2007, 28(1): 1-10.
[22]雷华阳,王学超,丁小冬,等. 软土主次固结划分及影响因素探讨[J]. 工程地质学报,2014, 22(3): 489-497.
Lei Huayang, Wang Xuechao, Ding Xiaodong, et al. Exploration on Division of Primary-Secondary Consolidation and Influential Factors with Soft Soil[J]. Journal of Engineering Geology, 2014, 22(3): 489-497.
[23]王丽琴,邵生俊,赵聪,等. 黄土初始结构性对其压缩屈服的影响[J]. 岩土力学, 2018, 39(9): 3223-3228.
Wang Liqin,Shao Shengjun, Zhao Cong, et al. Compression Curve Characteristic of Undisturbed Loess[J]. Rock and Soil Mechanics, 2018, 39(9): 3223-3228.
[24]Wang H M, Ni W K, Liu H S, et al. Study of the Repeated Collapsibility of Undisturbed Loess in Guyuan, China[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(8): 6321-6330.
[25]Zhang Y, Zhang Y, Mei S H. Experimental Investigation on Creep Behavior of Clastic Rock[J]. E3S Web of Conferences, 2020, 165(6): 30-51.
[26]Wang J B, Liu X R, Wang T H. Experimental Study on Creep Property of Lime Mudstone[J]. Chinese Journal of Underground Space and Engineering, 2014,10(4):770-775.
[27]Li A R, Deng H, Zhang H J, et al. The Shear-Creep Behavior of the Weak Interlayer Mudstone in a Red-Bed Soft Rock in Acidic Environments and Its Modeling with an Improved Burgers Model[J]. Mechanics of Time-Dependent Materials, 2021, 27(1):1-18.
[28]李安潤,邓辉,王红娟,等. 水-岩作用下粉砂质泥岩含水损伤本构模型[J]. 水文地质工程地质, 2021, 48(2): 106-113.
Li Anrun, Deng Hui, Wang Hongjuan,et al. Constitutive Model of Water-Damaged Silty Mudstone Under Water-Rock Interactions[J]. Hydrogeology & Engineering Geology, 2021, 48(2): 106-113.
[29]么焕民,靳丹丹,马芳芳. Riemann-Liouville分数阶微积分的定义及其性质[J]. 哈尔滨师范大学自然科学学报,2011, 27(3): 20-22.
Yao Huanmin, Jin Dandan, Ma Fangfang, Definition of Rimann-Liouville Fractional Calculus and Its Propertie[J]. Journal of Natural Science of Harbin Normal University, 2011, 27(3): 20-22.
[30]Koeller R C. Applications of Fractional Calculus to the Theory of Viscoelasticity[J]. Journal of Applied Mechanics, 1984, 6(51):299-307.
[31]王学彬. 拉普拉斯变换方法解分数阶微分方程[J]. 西南师范大学学报(自然科学版),2016, 41(7): 7-12.
Wang Xuebin. The Laplace Transformation Method Solves Fractional-Order Differential Equations[J]. Journal of Southwest Normal University(Natural Science Edition), 2016, 41(7): 7-12.
[32]薛定宇. 分数阶微积分学与分数阶控制[M]. 北京:科学出版社, 2018.
Xue Dingyu. Fractional-Order Calculus with Fractional-Order Control[M]. Beijing: Science Press, 2018.
[33]谭晓慧,余伟,沈梦芬,等. 土-水特征曲线的试验研究及曲线拟合[J]. 岩土力学,2013, 34(2): 51-56.
Tan Xiaohui,Yu Wei,Shen Mengfen, et al. Experimental Study and Curve Fitting of Soil-Water Characteristic Curve[J]. Rock and Soil Mechanics, 2013, 34(2): 51-56.
