虹吸排水法处理软土地基的水位与沉降计算模型
2024-02-27袁帅王君吴朝峰沈青松舒俊伟孙红月
袁帅 王君 吴朝峰 沈青松 舒俊伟 孙红月
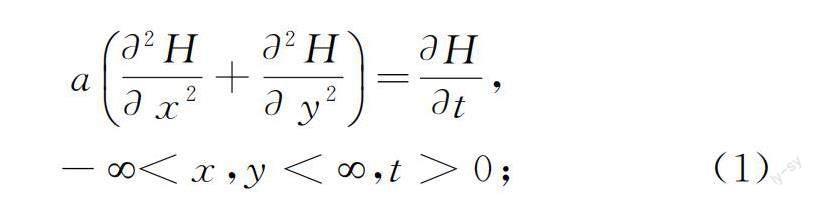
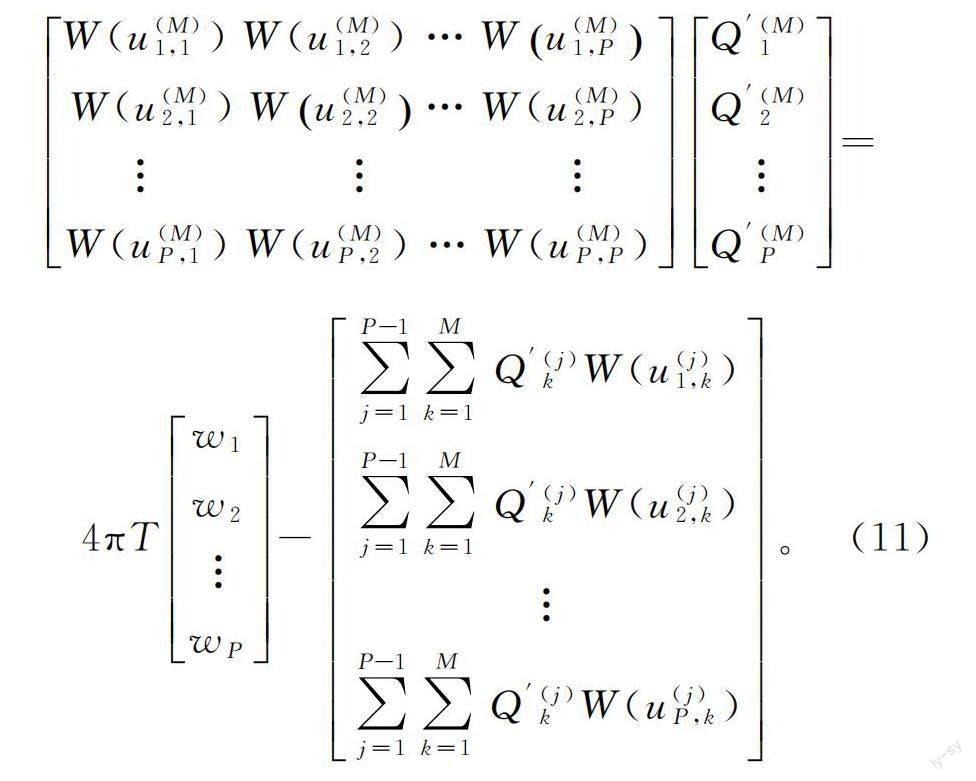
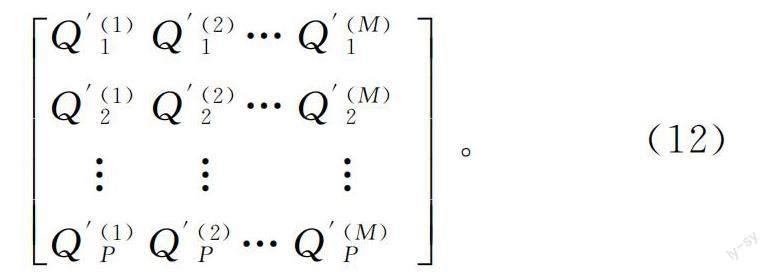
摘要:軟土具有渗透性差、承载力低等特性,软土地基的处理一直是岩土工程中的一大难题。利用虹吸免动力排水的特点,可将虹吸排水法应用于软土地基处理中,达到改善土体性质的目的。本文针对虹吸排水法独特的定降深降水模式,先基于离散化的Theis井流模型以及非线性的分层总和法,构建了以孔隙率为核心、渗透系数与压缩模量随固结情况改变的水位与沉降动态计算模型,并与数值模拟结果对比,然后从土体渗透系数、排水板间距以及场地大小3个方面对虹吸排水法处理软土地基的效果进行了分析。结果表明:数值模拟结果验证了计算模型的可靠性,对于浙江沿海不同渗透系数的土体,虹吸排水法均可起到良好的排水固结作用;调整排水板间距可对排水固结时间以及地下水位线起到显著控制作用;排水带来的附加应力随着场地面积的增大向土体深处延伸,对于面积50 m×50 m大小的场地,有效影响深度可达到地表以下27.31 m,远远超出虹吸扬程的极限。在实际的大面积软土地基处理中,虹吸排水法可发挥更好的作用。
关键词:软土;虹吸排水;地基沉降;非稳定流;井群干扰
doi:10.13278/j.cnki.jjuese.20220095
中图分类号:TU470
文献标志码:A
收稿日期:2022-04-04
作者简介:袁帅(1998-),男,硕士研究生,主要从事岩土工程和地质工程方面的研究,E-mail: 3160100846@zju.edu.cn
通信作者:孙红月(1970-),女,教授,博士生导师,主要从事岩土工程和地质工程方面的研究,E-mail:shy@zju.edu.cn
基金项目:国家自然科学基金项目(42230702)
Supported by the National Natural Science Foundation of China (42230702)
Calculation Model for Water Level and Settlement of
Soft Foundation Treated by Siphon DrainageYuan Shuai1, Wang Jun1,2,Wu Zhaofeng3,Shen Qingsong4, Shu Junwei4, Sun Hongyue1
1. Ocean College, Zhejiang University, Zhoushan 316021, Zhejiang, China
2. Ningbo China Communications Water Transportation Design and Research, Ningbo 315042, Zhejiang, China
3. China Energy Engineering Group Zhejiang Energetic Power Design Institution, Hangzhou 310012, China
4. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China
Abstract: Soft soil has the characteristics of poor permeability and low bearing capacity. The treatment of soft soil foundation is always a major problem in geotechnical engineering. With the characteristics of free power in drainage, the siphon drainage method can be applied in soft ground the treatment to improve the properties of the soil. Based on the discretized Theis well flow model and the nonlinear layered summation method of settlement, this paper constructs a water level and settlement calculation model considering the changes in permeability coefficient and compressive modulus by settlement with porosity as the core for the unique fixed-deck precipitation model of the siphon drainage method. The effect of the siphon drainage method in soft foundation treatment is analyzed from the aspects of soil permeability coefficient, drainage board spacing, and site size. The results mainly focus on the following three aspects. First, the calculation outcomes are compared with numerical simulation results and the reliability of the calculation model is verified. And the siphon drainage method can perform well in drainage and consolidation for soils of different permeability coefficients in Zhejiang coastal areas. Second, adjusting the spacing of drainage plates can significantly control the drainage consolidation time and the groundwater level. Third, the additional stress caused by drainage will extend into the soil as the site area increases, and for a 50 m×50 m site, the effective influence depth can reach 27.31 m below the surface, which is far beyond the limit of siphon lift. Therefore, the siphon drainage method will get a better effect in practical large-area soft soil foundation treatment.
Key words: soft soil; siphon drainage; foundation settlement; unsteady flow; well group interference
0 引言
包括軟土在内的软弱土和不良土在我国地基土中占了很大比例,在沿海地区尤为明显[1]。除天然生成外,人类活动也产生了大量的人工软黏土,此类软黏土作为地基或填土等使用时,一般要对其进行加固处理,以提高其强度和稳定性[2]。
以井点降水法、真空预压法和堆载预压法为代表的排水固结法是处理软土地基最常用的方法[3-4]。对于低渗透性软土,其排水固结将是一个长期的工程,当采用井点降水法和真空预压法从软土中抽水时,需要水泵不间断工作,能耗很大且排水效率较低,其动力系统也存在一定的安全隐患[5-6]。相较而言,虹吸排水法可以免动力实现地下水运输,减少能源的消耗,更高效和安全,符合当今绿色环保的发展理念。且相比于堆载预压法,采用虹吸排水法处理软土地基时,地下水运动的方向与水体所受重力方向一致,可以加速土体固结。其在边坡排水工程中已经得到了有效应用[7-9],在地基处理方面的可行性也已通过室内物理模型实验进行了验证[10-11],但其理论计算与数值模拟部分仍需进一步探索。
虹吸排水法处理软土地基时,将虹吸管一端插入透水管中,打入地基的透水层内,并将虹吸管另一端放入打设好的集水井中。启动虹吸后,软土中的水将汇集到透水管中,并被虹吸管抽出。由于大气压的限制,虹吸扬程无法超越10.33 m的极限,虹吸管打入土体的深度超过虹吸极限扬程即可保证虹吸管口永远浸没在地下水中,不会出现断流的情况。通过智能控制器控制集水井中的水位,令其保持在低于虹吸极限扬程深度,使虹吸管两端存在水位差,虹吸排水过程即可持续进行。随着土体中地下水位的下降,土体的有效应力不断增大,进而发生固结,达到地基处理的目的。
许多学者对井流理论与地下水位下降引起的土体沉降进行了大量的理论研究。如:Theis[12]针对无限含水层中的承压井流提出了定流量抽水的计算公式,奠定了非稳定井流理论的基础;Neuman[13]针对潜水含水层单井抽水的情况,分别给出了完整井和非完整井的井流公式;Barron[14]给出了理想井竖井地基固结的解答;谢康和等[15]研究了影响区真实形状为正六边形的竖向排水井地基固结的问题,并提出了普遍解析解;曹文贵等[16]提出了考虑附加应力影响的地基土变形模量确定方法。孟世豪等[17]通过结合沉降过程中的土体渗透系数以及水头的变化规律,提出了一个地下水流-地面沉降模型。但这些研究均只侧重井流或沉降的一方面,少有考虑这两个过程之间的耦合。
计算地基沉降较为全面的方法是采用比奥固结理论,但其计算较为繁琐、模型参数多且误差大,结果并不理想。在实际工程中参数选用合理时,可以简化并采用分层总合法进行计算[18]。规范方法虽然简便,但经验系数区间大,缺少科学的量化取值方法,准确度有待改进[19]。
不同应力水平下高含水率吹填淤泥的渗透系数差异极大,甚至会相差多个数量级[20]。而现有的非稳定流模型大多将土体渗透系数看做常数,未考虑固结过程中渗透系数的变化,这与实际情况有很大差距,会导致计算结果产生较大误差。
为保证应用的简易性,又兼顾计算精度,满足工程实践的需要,本文先采取动态的非线性分层总和法求解土体的沉降;然后针对虹吸排水法的定降深井群特点,考虑固结压缩过程中土体渗透系数与压缩系数等参数的改变[21],提出了新的计算模型,建立了一套综合考虑地下水流动与土体固结的算法;最后通过数值模拟并与室内物理模型对比验证了该算法的有效性。通过研究排水过程中孔隙水压力的变动与地基的沉降情况,探究了此方法的处理效果,以期对虹吸排水法处理软土地基的水位变动及沉降做出有效预测。
1 模型建立
在滨海地区,潜水含水层的水位接近于地表,其顶面与大气直接相连,且孔隙率很高,故可认为初始水位与地表齐平。相对于虹吸排水的速度,软土地基的渗透系数极小,高扬程虹吸流量可达10.4 L/h,远大于汇水速度[22],所以当土体中的水汇入透水管后,会在较短的时间内被虹吸管排出,可以认为透水管中的水位维持在虹吸极限深度。由于大气压的限制,在沿海地区极限深度约为10 m,故可将虹吸排水法处理软土地基的过程作为定降深抽水处理[23]。透水管侧壁与底部均可进水,但底部面积远远小于侧壁,进水量可忽略不计,模型的水位变动可看作完整井群作用下的潜水含水层定降深非稳定问题。
设含水层厚度为H0,初始水头高度位于地表,即初始水头高度为H0,排水井半径为rw,井中水头高度固定为Hw。将软黏土层视为潜水含水层,下面针对虹吸井群特点,建立三维渗流数学模型,并有如下假设:①土体为半无限体且符合均质、各向同性;②不考虑越流影响,也不考虑地表的补给与蒸发;③地下水流速分布满足Dupuit假定。
在三维直角坐标系中,各向同性潜水含水层完整井群潜水渗流运动方程为
初始条件为
边界条件为
式中:a为水力扩散系数,a=KH0/μ,K为渗透系数,μ为重力给水度;H、Hj为水头高度;xj、yj为各井点坐标;t为时间。
将含水层厚度作为计算压缩层厚度,将其分为N层,每层厚度为hi。实际工程中,应根据土体类型与各类土厚度灵活划分土层。本文将整個排水固结过程分为M段进行计算,每一时段对应一个叠加的井点与荷载,所以共有M个井点叠加,将上覆荷载按照时间顺序分为M级加载,则第i层地基在第k级荷载作用下发生的沉降量si,k为
式中:σi,k,εi,k分别为第i层地基在第k级荷载作用下的应力与应变;ei,k为第i层地基在第k级荷载作用前的压缩系数。
则地基总沉降量s为
计算沉降须确定有效应力变动及土体参数随荷载的变化情况。其中有效应力的变化根据土体中水位的变动情况确定,将其代入式(7)可得到新的孔隙率ni,k,再将ni,k代入式(8)得到新的压缩系数ei,k[24],即完成土体参数的更新。
式中:v为泊松比;α=(1+v)/2(1-2v);ei,k-1为第i层地基在第k-1级荷载作用后的压缩系数;ni,k,ni,k-1分别为第i层地基在第k级、第k-1级荷载作用后的孔隙率。
根据土体的初始参数,以及水位的变动带来的附加应力,由递推公式可得土体沉降并更新土体变形参数,再进行下一级计算,实现动态求解。
2 模型求解
对于定降深井群问题,由于其边界条件的非线性以及流量的不确定性,使得问题的解很难通过正常的理论推导解出。但可将其流量离散化,然后用阶梯流量公式进行计算,如图1所示。可将定降深井认为是从t0至t1时刻的定流量抽水井,流量为Q1;而在t1时刻起加入一个(Q1-Q2)的定流量注水井(如果Q1-Q2<0,则为抽水井),以此类推,可将其转换为位置重合的多个定流量井,并进行线性叠加,然后利用泰斯公式进行求解即可[25]。
对一单井来说,可将排水过程分为M个时段,设定每个时段内的流量为常数,将该井转化为M口定流量井的叠加进行分析[26]。则此井对渗流场中任一点处的降深wxy,可以用这M口定流量井对该点降深的叠加来实现,数学表达式为
式中:T为导水系数,T=KH0;Q′1=Q1,Q′2=Q2-Q1,…,Q′M=QM-QM-1;W(ui)为井函数;ui=r2/4aT(t-ti),其中,i=1,2,…,M,ti为对时间的离散,r为此点与排水井的距离。
对一个有P口抽水井的地基来说,将排水过程分成M个时段,任意一口井处水位wl的变动受到所有P口井的影响,可由式(10)来表示:
对所有井点可做类似处理,并将其联立,然后改写为矩阵形式:
式中:Q′(j)k为第j口井在第k时段的流量;Q′(j)k=Q(j)k-Q(j-1)k;W(u(M)j,k)为第j口井在第k时段对于井点的井函数。
在各抽水井降深已知的情况下,解方程组可得到任意一口井在各时段的流量,用矩阵形式写为
得到所有抽水井的流量变化情况后,可利用式(13)计算土体中任一点处的水位降深变化情况:
得到各排水井水位随时间的变化情况后,可将土体分为疏干区和饱和区(图2)。将原水位线与降水后水位线之间的土体定义为疏干区,一直处于水面线以下的土体定义为饱和区,分别计算其应力变化。
疏干区土体有效应力的增量,来自于水位变化带来的有效应力改变,按照有效应力的定义,降水后的第N层土体的有效应力增量Δσ1为
式中:γi为i层土的天然重度;γw为水的重度;γsat,i为i层土的饱和重度。
水位线以下的饱和区域深度h处水位变动带来的有效应力增量的大小为
Δσ2=whγi+γw-γsat,ifh。 (15)
式中:wh为水位降深;fh为均布荷载下深度h处Mindlin解对应的应力分布系数。
得到应力变化情况后,按照式(16)对各土层的应变值进行计算:
εi=σi/ei(16)
将各土层压缩值代入式(7)和(8),得到该级荷载作用后土体的孔隙率与压缩系数,并进行下级荷载的计算。基本计算流程见图3。
3 数值模拟与理论解对比分析
3.1 ABAQUS数值模型建立
为了验证理论解的正确性,本文开展了相应的数值模拟进行对比分析。本文基于比奥固结理论,利用数值软件ABAQUS来模拟虹吸排水法处理软土地基过程中的水位变动与土体沉降情况,建立了软土地基排水的有限元模型。
塑料排水板采用正方形排列,间距1 m。虹吸扬程取10 m。对于排水板,可将其按照等效直径的圆形砂井进行换算,其等效直径dw可按照式(17)[27]计算:
dw=β(c+d)/2 。 (17)
式中:β为排水板等效直径换算系数;c、d分别为排水板的宽度与厚度。
根据地基处理手册[28],排水板打设深度在10 m时,β=0.75,故可近似取塑料排水板等效直径为4 cm。
为了简化计算并便于工程应用,忽略各井点对超出最大影响半径之外的井点的干扰。根据库萨金公式,各井点的最大降水影响半径R可按照式(18)进行计算:
土体模型采用修正剑桥模型,水平方向上取两排水板之间区域作为计算区域进行分析,竖直方向上取含水层厚度15 m作为计算层。模型的左右两侧约束水平方向移动;底部约束水平、竖直方向移动;排水井侧壁约束水平方向移动。土体表面孔隙水压力固定为0;模型底部为不透水边界,排水井侧壁为排水边界;土体设置为孔隙介质,采用相应的四结点平面应变四边形单元、双线性位移、双线性孔压(CPE4P单元)。为了着重研究两排水井间水位情况,对该部分的网格进行了加密处理。总分析时长为100 d,每个分析步长为1 d。
由于土层从上到下初始应力状态是不同的,导致初始孔隙比与土体密度也不同。按照修正剑桥模型理论,处于K0固结状态土体的孔隙比e0为
式中:e1为INCL(初始等向固结线)的截距;λ为INCL的斜率;κ为半对数坐标系下压缩回弹曲线的斜率;p′0为初始屈服力大小;p′为平均有效应力;ecs为CSL(临界状态線)的截距,ecs=3;q为偏应力;U为破坏常数。
在不考虑堆载与其他外部荷载的情况下,ABAQUS中应当采用Gravity荷载类型对土体施加自重应力,根据土体三相比例指标之间的关系,可以得到土体密度之间的关系
式中:ρd为土体干密度;ρsat为土体饱和密度;ρw为水的密度。
根据刘用海[29]对宁波地区软土工程性质的调查,修正剑桥模型所采用的参数如表1所示。利用用户子程序VOIDRI以及Distribution功能可将孔隙比和干密度沿深度方向的分布导入数值模型,更符合实际情况,避免因将一块土体设置为同一参数,忽略土体参数沿深度方向变化带来的误差。将各参数导入ABAQUS程序中,即可求得虹吸排水法处理软土地基的水位变动以及土体沉降结果。
3.2 对比分析
两虹吸排水管中点10 m深度处孔隙水压力随时间的变化情况如图4所示,不同时刻孔隙水压力径向分布情况见图5。由图4可见,孔隙水压力值随着排水过程的进行呈指数型下降,且在排水总时长100 d后,理论解与数值解的孔隙水压力消散均超过了90%,这表现出虹吸排水法具有良好的处理效果。由图5可知:不同时刻孔隙水压力的径向分布近似呈漏斗状;各点的孔隙水压力值随时间均逐渐下降,并趋于稳定,且越靠近排水井处,下降的幅度越大。
图6显示了两虹吸排水管中点处地表沉降量随时间的变化情况,可见其趋势与孔隙水压力的减小量基本一致,但存在一定滞后,达到基本稳定所需的时间更久。图6中理论解与数值模拟解保持了一致性,说明两者符合良好。
4 软土虹吸排水的应用
4.1 虹吸排水法可行性分析
虹吸排水法处理软土地基的关键在于有效降低土体中的地下水位,从而使土体固结沉降,提高其承载力。浙江沿海地区淤泥质粉质黏土的矿物成分以亲水的活动性矿物为主,渗透系数较小,垂直方向上渗透系数均值为2.123×10-7 cm/s,变化范围在0.22×10-7 ~ 4.31×10-7 cm/s之间;水平向上渗透系数均值为3.941×10-7 cm/s,变化范围在0.29×10-7~ 22.50×10-7cm/s之间[25]。为了验证虹吸排水法的可行性,取土体渗透系数为2×10-8 ~ 2×10-6 cm/s,以4口排水井呈正方形排列为例对地基处理的效果进行分析。设地基厚度为20 m,其余参数保持不变的前提下,地基中心处土体孔隙水压力的消散以及地基的固结沉降情况如图7—图9所示。
由图7、图8可以看出,渗透系数对于虹吸排水法处理软土地基的效果有着较大的影响。在渗透系数较小(2×10-8、1×10-7 cm/s)时,土体中水位的下降较为缓慢,且100 d后还未达到较为稳定的状态;而在渗透系数较大(>5×10-7cm/s)时,土体能在较短时间内完成排水固结,最终的水位下降与土体沉降量也更为显著。渗透系数较小(2×10-8、1×10-7 cm/s)的孔隙水压力曲线和沉降曲线之间间距较大,渗透系数较大(>5×10-7cm/s)的曲线之间间距较小;表明渗透系数在较小时较为敏感,而当其增大到一定程度时,对最终的处理效果敏感性较低。
图9显示了排水固结100 d后,不同渗透系数下中心点处土体的分层沉降量情况。对于浅层疏干区(0 ~ 8 m),在不同渗透系数下表现出相同的沉降规律,近似随深度增加线性增加;对于水面线以下的饱和区,其受到的扰动随深度增加急剧减小,其中13 m以下的土体基本保持原状,沉降量值可忽略不计。
但由图7可见,对于不同渗透系数的土体,孔隙水压力的下降均超过60 kPa,即地表潜水位的下降均超过6 m,结合图9可知,从分层沉降量看,降水对于土体的影响均超过10 m;表明虹吸排水法对于10 m深度内的软土地基均可以取得较好的处理效果。
除了土体自身因素,排水井的布置也会对地基处理效果产生很大的影响,其中排水井间距的影响较为显著。在考虑地基处理效果与经济因素的基础上,选取0.5 ~ 4.0 m作为井间距展开分析,渗透系数取3×10-7 cm/s,其余条件不变。图10、图11描述了中心点处10 m深度孔隙水压力及地表沉降量随时间的变化情况。由图10可见:排水井间距较小(0.5、1.0 m)时,孔隙水压力会迅速下降,近似呈指数状,并稳定在较低水平,土体也会快速固结沉降;排水井间距较大(2.0、4.0 m)时,孔隙水压力的下降非常缓慢,近似呈线性,排水100 d后仍未达到稳定状态,土体沉降情况与之对应。对于0.5 m與4.0 m的间距,100 d后后者残余的孔隙水压力约为前者的9倍,沉降量约为前者的一半;这表明改变间距可以有效控制处理效果及工期,以适应不同的情况。
图12显示了不同排水井间距下分层沉降量的情况,随着井间距的增大,分层沉降量的峰值减小,对饱和区土体,其影响随深度增大更平缓地减小;这是因为随着间距的增大,降水带来的附加应力分布范围更大,能够扩散到更深部的土体。
4.2 影响深度
从井间距的分层压缩情况可以得到,地基处理的范围会对中心点处的沉降量产生较大影响。由于自重应力随深度增大,而附加应力则随深度减小;因此超过一定深度处的土体变形对总沉降量影响很小,该深度称为地基沉降计算深度,可采用式(23)来确定
Δσz≤δσcz。 (23)
式中:Δσz为深度z处的附加应力;δ为常数,对于软土δ=0.1,σcz为深度z处的自重应力。
设定场地大小为5 m×5 m ~ 50 m×50 m,排水板间距1.0 m,含水层厚度30 m,对中心点处水位降深以及地基的影响深度进行计算,结果如表2所示。不同场地大小下中心点处水位降深无明显变化,水位降深为7.2 m,但场地面积的扩大对于附加应力向土体深处的延伸有着非常显著的提升,也会大幅提升影响深度,使深层土体更充分固结,从而提高地基处理的效果。图13描绘了中心点处30 m内的分层压缩情况,可以看到水面线以上疏干土体的沉降基本不受场地大小的影响,而饱和区域变化较大。场地面积较小时,饱和区受到的影响随深度增长迅速减小;随着场地面积的扩大,饱和区的压缩固结情况有很大改善,深处的土体也会得到有效处理且效果大大提高。这是由于在半无限土体中,随着场地面积的扩大,处理区降水带来的附加应力向饱和区土体深处扩散范围更大,影响深度也更深,这会对土体的固结压缩带来有利的影响,从而提升总体的处理效果。
5 结论
1)针对虹吸排水定降深井群降水的特点,基于Theis井流模型以及非线性分层总和法,建立了虹吸排水法处理软土地基的水位与沉降动态计算模型,并通过离散的方法,推导井群作用下虹吸排水法处理软土地基过程中水位与沉降的理论解。
2)通过与ABAQUS数值模拟解的对比验证,所推求的解析解可以较好地反映水位与土体固结沉降的变化规律,且该理论解的求解相对于传统方法更为简便,工程适用性更强。
3)土体影响深度受到场地大小的影响,在水位降深不变的情况下,地基处理范围的扩大可显著提高中心点下有效应力增量的扩散深度,从而加大地基处理的有效深度。
4)虹吸排水法对于沿海地区不同渗透系数的软土均可起到较好的处理效果。排水固结100 d后,中心点处孔隙水压力下降均大于60 kPa;对于不同性质的软土,通过改变排水板间距的方法能够有效地控制地基处理效果以及排水固结时间,中心点处孔隙水压力消散以及土体固结沉降可在10 d内达到90%以上。
参考文献(References):
[1]刘之葵.岩土工程勘察[M].北京:中国建筑工业出版社, 2012.
Liu Zhikui. Geotechnical Engineering Investigation[M]. Beijing: China Construction Industry Press,2012.
[2]吴邦颖.软土地基处理[M].北京:中国铁道出版社,1995.
Wu Bangying. Soft Soil Foundation Treatment[M]. Beijing: China Railway Publishing House, 1995.
[3]郑刚, 龚晓南, 谢永利, 等. 地基处理技术发展综述[J].土木工程学报, 2012, 45(2):127-146.
Zheng Gang, Gong Xiaonan, Xie Yongli, et al. State-of-the-Art Techniques for Ground Improvement in China[J]. China Civil Engineering Journal, 2012, 45(2):127-146.
[4]苏亮, 时伟, 水伟厚,等. 高能级强夯法处理深厚吹填砂土地基现场试验[J].吉林大学学报(地球科学版), 2021, 51(5): 1560-1569.
Su Liang, Shi Wei,Shui Weihou,et al. Field Test of High Energy Dynamic Compaction on Hydraulic Sandy Filling[J]. Journal of Jilin University (Earth Science Edition), 2021, 51(5): 1560-1569.
[5]Kjellman W. Consolidation of Clayey Soils by Atmospheric Pressure[C]//Proceedings of a Conference on Soil Stabilization. Boston: Massachusetts Institute of Technology, 1952: 258-263.
[6]Cai Yuanqiang, Qiao Huanhuan, Wang Jun, et al. Experimental Tests on Effect of Deformed Prefabricated Vertical Drains Indredged Soil on Consolidation via Vacuum Preloading[J]. Engineering Geology, 2017, 222: 10-19.
[7]Sun H Y, Wang D F, Shang Y Q, et al. An Improved Siphon Drainage Method for Slope Stabilization[J]. Journal of Mountain Science, 2019, 16(3):701-713.
[8]雷怡,帥飞翔,孙红月,等.边坡负压排水非稳定流研究[J].吉林大学学报(地球科学版),2022, 52(1):162-170.
Lei Yi, Shuai Feixiang, Sun Hongyue, et al. Study on Unsteady Flow of Slope Self-Starting Drainage Method[J]. Journal of Jilin University (Earth Science Edition), 2022, 52(1): 162-170.
[9]曹长鑫,孙红月.黄土地区边坡虹吸排水孔间距优化[J].吉林大学学报(地球科学版),2021,51(4):1152-1159.
Cao Changxin, Sun Hongyue. Optimization of Siphon Drainage Hole Spacing on Slope in Loess Region[J]. Journal of Jilin University (Earth Science Edition), 2021, 51(4): 1152-1159.
[10]Sun H Y, Wu G, Liang X, et al. Laboratory Modeling of Siphon Drainage Combined with Surcharge Loading Consolidation for Soft Ground Treatment[J]. Marine Georesources & Geotechnology, 2018, 36(8):940-949.
[11]吴纲.软土地基虹吸排水理论分析与模型试验[D].杭州:浙江大学,2019.
Wu Gang. Theoretical Analysis and Model Test of Siphon Drainage in Soft Soil Foundation[D]. Hangzhou: Zhejiang University, 2019.
[12]Theis C V. The Relation Between the Lowering of the Piezometric Surface and the Rate and Duration of Discharge of a Well Using Groundwater Storage[J]. Transactions American Geophysical Union, 1935, 16(2): 519-524.
[13]Neuman S P. Theory of Flow in Unconfined Aquifers Considering Delayed Response of the Water Table[J]. Water Resources Research, 1972, 8(4):1031-1045.
[14]Barron R A. Consolidation of Fine-Grained Soils by Drain Wells by Drain Wells[J]. Transactions of the American Society of Civil Engineers, 1948, 113(1): 718-742.
[15]谢康和,余坤,童磊,等.考虑影响区真实形状的竖向排水井地基固结解[J].岩土力学,2011,32(10):2944-2950.
Xie Kanghe, Yu Kun, Tong Lei, et al. Analytical Solution for Consolidation by Vertical Drains Considering Actual Shape of Influence Zone[J]. Rock and Soil Mechanics, 2011,32(10): 2944-2950.
[16]曹文贵,邓湘君,张超.基于Duncan-Chang模型的地基沉降分层总和分析方法探讨[J].岩土工程学报,2013,35(4):643-649.
Cao Wengui, Deng Xiangjun, Zhang Chao. Layerwise Summation Method for Ground Foundation Settlement Based on Duncan-Chang Constitutive Model[J]. Chinese Journal of Geotechnical Engineering,2013,35(4): 643-649.
[17]孟世豪,崔亚莉,田芳,等.基于MODFLOW-SUB建立变渗透系数的地下水流-地面沉降模型[J].吉林大学学报(地球科学版),2022, 52(2):550-559.
Meng Shihao, Cui Yali, Tian Fang, et al. Modeling of Groundwater Flow-Land Subsidence with Variable Hydraulic Conductivity Based on MODFLOW-SUB[J]. Journal of Jilin University (Earth Science Edition), 2022, 52(2): 550-559.
[18]李琳,张建根,杨敏. 疏干降水引起坑后地面沉降的一种简化计算方法[J].岩土工程学报,2008,30(增刊1):306-309.
Li Lin, Zhang Jiangen, Yang Min. Simplified Analysis of Settlement due to Dewatering of Foundation Pits[J]. Chinese Journal of Geotechnical Engineering, 2008,30(Sup.1):306-309.
[19]杨光华,黄致兴,李志云,等.考虑侧向变形的软土地基非线性沉降计算的简化法[J].岩土工程学报,2017,39(9):1697-1704.
Yang Guanghua,Huang Zhixing,Li Zhiyun,et al. Simplified Method for Nonlinear Settlement Calculation in Soft Soil Considering Lateral Deformation[J]. Chinese Journal of Geotechnical Engineering, 2017,39(9): 1697-1704.
[20]蔡袁强.吹填淤泥真空预压固结机理与排水体防淤堵处理技术[J].岩土工程学报,2021,43(2):201-225.
Cai Yuanqiang. Consolidation Mechanism of Vacuum Preloading for Dredged Slurry and Anti-Clogging Method for Drains[J]. Chinese Journal of Geotechnical Engineering, 2021,43(2):201-225.
[21]曹文贵,田小娟,刘海涛,等.条形基础下地基非线性沉降的改进计算方法[J].岩石力学与工程学报,2009,28(11):2266-2272.
Cao Wengui, Tian Xiaojuan, Liu Haitao, et al. Improved Method for Calculating Nonlinear Settlements of Strip Foundation[J]. Chinese Journal of Rock Mechanics and Engineering, 2009,28(11):2266-2272.
[22]Mei C, Liang X, Sun H, et al. High-Lift Siphon Flow Velocity in a 4 mm Siphon Hose[J]. Journal of Zhejiang University:Science A, 2017, 18(6): 487-495.
[23]吴纲, 孙红月, 付崔伟, 等.软土虹吸排水完整井非稳定流模型及解析解[J]. 岩土力学, 2018, 39(9):3355-3361,3384.
Wu Gang, Sun Hongyue, Fu Cuiwei, et al. A Mathematical Model and Its Solution for Unsteady Flow Under Siphon Drainage by Fully Penetrating Well in Soft Ground[J]. Rock and Soil Mechanics, 2018, 39(9):3355-3361,3384.
[24]曹文貴,李鹏,许烜,等.考虑模量变化与三维应力影响的地基沉降分析方法[J].湖南大学学报(自然科学版),2018,45(3):142-148.
Cao Wengui, Li Peng, Xu Xuan, et al. An Analystic Method of Ground Foundation Settlement Influenced by Modules Change and Three-Dimension Stress[J]. Journal of Hunan University (Nature Science), 2018,45(3):142-148.
[25]陈崇希, 林敏. 地下水动力学[M]. 武汉: 中国地质大学出版社, 1999.
Chen Chongxi, Lin Min. Groundwater Dynamics[M]. Wuhan: China University of Geoscience Press, 1999.
[26]姚旭初,万力,苏学清.基坑降水中非稳定井流计算[J].工程勘察,1999,27(3):30-33.
Yao Xuchu,Wan Li,Su Xueqing. Calculation of Unsteady Well Flow in Foundation Pit Dewatering[J]. Engineering Investigation,1999,27(3):30-33.
[27]Hansbo S, Jamiolkowski M, Kok L. Consolidation of Soil by Vertical Drains[J]. Geotechnical Investigation & Surveying,1981, 31(1): 45-66.
[28]地基处理手册编写委员会.地基处理手册[M].北京:中国建筑工业出版社,1986:63-67.
Compilation Committee of the Handbook of Foundation Treatment. Handbook of Foundation Treatment[M]. Beijing: China Construction Industry Press, 1986:63-67.
[29]刘用海. 宁波软土工程特性及其本构模型应用研究[D].杭州:浙江大学,2008.
Liu Yonghai. Engineering Characteristics of Ningbo Soft Soil and Its Constitutive Model Application[D]. Hangzhou: Zhejiang University,2008.
