一种增加辅助子模块的MMC 改进混合调制控制策略

杨光源，周诗嘉，彭光强，武霁阳，辛清明，许树楷

（1.中国南方电网超高压输电公司检修试验中心，广州 510663；2.南方电网科学研究院有限责任公司，广州 510080）

相比于传统的两电平和三电平换流器，模块化多电平换流器MMC（modular multilevel converter）因其具有电压等级高、可靠性高和输出波形优良等技术优势，在高压电力传动和柔性直流输电等大功率场合被广泛运用[1-4]。

近年来，国内外学者对于MMC 的研究主要集中在系统结构[5-6]、改进调制策略和均压控制方法[7-8]及环流抑制[9]等方面。现行的主流MMC 子模块采用的都是半桥式结构，具有成本低和控制简单的优点。为了使MMC 能够具有直流故障电流抑制能力，在提出半桥MMC 结构的基础上，Marquardt 教授又提出了全桥子模块FBSM（full-bridge sub-module）和箝位双子模块CDSM（clamping double sub-module）的新型子模块拓扑[10-11]。

MMC 作为目前直流输电主流的变流器拓扑，其输出波形会对输电产生重要影响。传统MMC 每个桥臂串联N 个半桥子模块，每当投切一个子模块，其电压跳变恰为一个子模块电容电压。当子模块个数较少时，MMC 输出电平数量减少，输出波形谐波畸变率较高。针对这种情况，如果在传统半桥MMC 中串入全桥子模块，控制其电容电压为半桥子模块的1/2，就可以将电容电压的跳变减小，输出电流谐波畸变率就会随之降低。

由于新的MMC 拓扑中的子模块含有半桥和全桥两种结构，且全桥子模块的电容电压要控制为半桥子模块的1/2，这容易造成不同子模块间的能量失衡，因此需要对MMC 的子模块电容电压平衡策略进行重新设计[2]。文献[12]和文献[13]提出了一种改进的载波移相调制方法，可以对MMC 输出波形进行优化，但是该方法不适用于中高压场合，而且由于采用载波调制，系统需要增加PI 控制器维持子模块电容电压的平衡，且载波移相调制对IGBT的开关能力要求较高。文献[14]提出一种改进的混合调制方法，通过增加一个全桥子模块，可以将MMC 电平数增加一倍，降低MMC 输出波形的谐波畸变率，但是由于全桥子模块采用载波控制，其开关频率会大幅提高，从而导致系统的开关损耗也有所提高。

因此，本文在文献[14]的基础上，对其混合调制策略进行改进，增加一个全桥子模块调制信号的调节量，使得桥臂串入的全桥子模块的电容电压更容易平衡。

此外，本文在尽可能降低输出电流谐波畸变率的前提下，通过减少全桥子模块的投入时间，降低全桥子模块的开关频率，并给出了两者之间的动态关系。

最后，通过Matlab/Simulink 软件搭建仿真模型验证改进型混合调制策略应用于本文MMC 拓扑的可行性和有效性。

1 改进型MMC 拓扑结构和工作原理

传统三相MMC 的拓扑结构中，每个桥臂由N个子模块串联而成，子模块采用半桥结构，每相有上、下两个桥臂。当半桥子模块中上桥臂IGBT 或其并联二极管导通时，该子模块处于投入状态，输出电压为电容电压；当半桥子模块中下桥臂IGBT 或其并联二极管导通时，该子模块处于切除状态，输出电压为零。子模块的充放电与流入子模块电流的方向有关。假定直流侧电压为Udc，那么半桥子模块的电容电压UC可以表示为

图1 所示为本文采用的MMC 拓扑结构，其中，HBSM 为半桥子模块，FBSM 为全桥子模块，L0为桥臂电感，C 为子模块电容，直流侧电压为Udc，全桥子模块的电容电压值为半桥子模块的1/2。

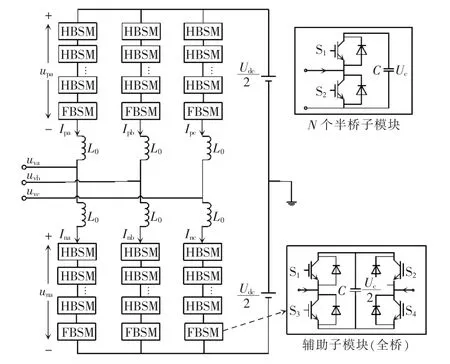
图1 改进型MMC 拓扑结构Fig.1 Topology of improved MMC

正常运行状态下的半桥子模块有2 种工作状态：UC，0。由于半桥子模块较为常见，其工作状态这里不作过多阐述。正常运行状态下的全桥子模块有3 种工作状态：UC，0，-UC。如表1 所示，假定全桥子模块的四个开关器件的开关状态分别为S1，S2，S3，S4，S1和S3互补导通，S2和S4互补导通，“1”表示器件导通，“0” 表示器件断开。以1/2 全桥子模块为例，全桥子模块具体的工作状态如表1 所示。

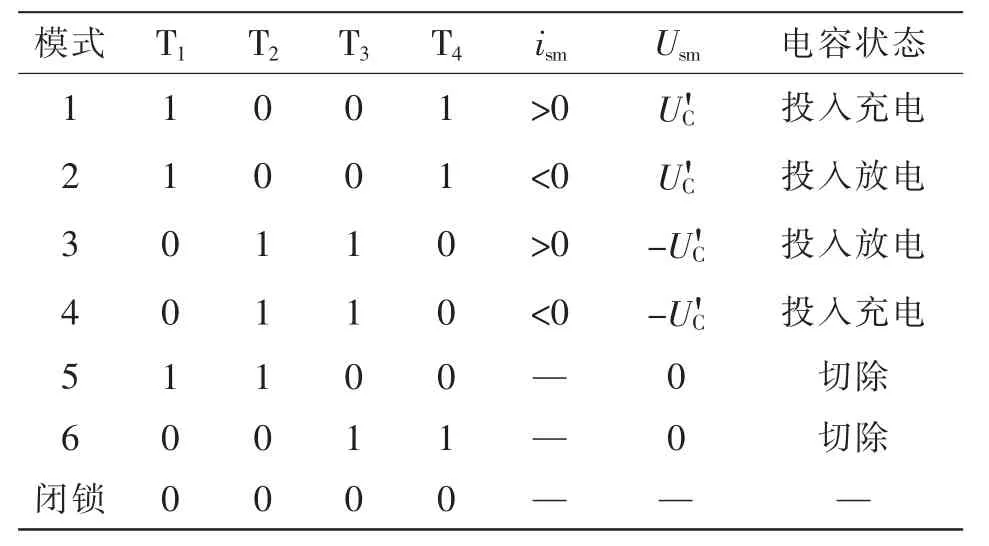
表1 全桥子模块工作状态Tab.1 Operation states of full-bridge sub-module

由于1/2 辅助子模块的电容电压值为半桥子模块的1/2，所以1/2 辅助子模块的电容电压U'C可表示为

2 改进型MMC 数学模型

根据图1 可以看出，由于每个桥臂的各器件的参数和工作原理都完全相同且对称，那么对于三相改进型MMC 的数学建模可以用其中一相来分析。以A 相为例，单相改进型MMC 的等效拓扑如图2所示。

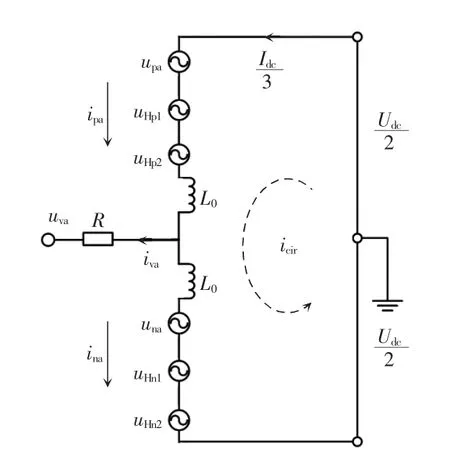
图2 单相改进MMC 拓扑Fig.2 Topology of single-phase improved MMC

图中：upa和uHp分别为上桥臂半桥和1/2 辅助子模块的等效电压源电压；ipa为上桥臂的电流；una和uHn1分别为下桥臂半桥和1/2 辅助子模块的等效电压源电压；ina为下桥臂的电流；L0为桥臂电感值；R 为负载侧电阻；icir为桥臂和直流侧之间的环流。

根据文献[15]，结合图2 的等效电路图，在不考虑系统环流和电抗间的互感情况下，根据基尔霍夫电压定律可得

针对本文调制策略，上、下桥臂的半桥子模块投入子模块的电容电压之和始终保持为N·UC，上、下桥臂1/2 全桥子模块输出电压之和始终保持为0，因此有

结合式（4）～式（7）可得，上、下桥臂1/2 辅助子模块的参考电压为

式中，npa和nna分别为上、下桥臂投入子模块的个数。

由于1/2 辅助子模块的电容电压为半桥子模块的1/2，在计算需要投入的子模块个数时，uHp1，pwm和uHn1，pwm除以半桥子模块电容电压，即1/2 辅助子模块参考投入个数的取值范围是0～1/2，这为后文1/2 辅助子模块投切时投切区段的划分提供了理论依据。

3 改进型MMC 的调制策略

根据上述分析，本文的MMC 拓扑中每个桥臂均含有两种类型的子模块，且要将全桥子模块的电容电压控制为半桥子模块的1/2。如果采用传统的NLM 调制方法，根据文献[14]可知，半桥子模块和全桥子模块的充放电会出现能量失衡，进而导致MMC 系统无法正常运行[13]。为了平衡新的MMC 拓扑中不同子模块充放电的均衡，需要对原有的MMC平衡控制策略进行改进，使得系统的能量守恒。

3.1 半桥子模块的平衡控制策略

对于半桥子模块的控制，采用传统的NLM 控制策略，取整函数采用去尾的floor（n）函数，其调制策略的流程如图3 所示。

图3 NLM 调制流程Fig.3 Flow chart of NLM modulation

3.2 1/2 辅助子模块的平衡控制策略

记经floor（n）函数前后子模块个数的差值为t，即t=n-floor（n）。为了实现辅助子模块的稳压控制，应使得每一时刻辅助子模块的电容电压之和尽可能的接近于t·UC。假定每一时刻需要额外投入a 个半桥子模块，1/2 辅助子模块的开关状态记为Kpwm，则辅助子模块的稳压控制可以表示为

图4 所示即为本文所提MMC 拓扑平衡控制策略的整体流程。根据图4 可以看出，全桥子模块的投切取决于差值t 的取值范围，根据t 是否为整数可分为以下两种情况：

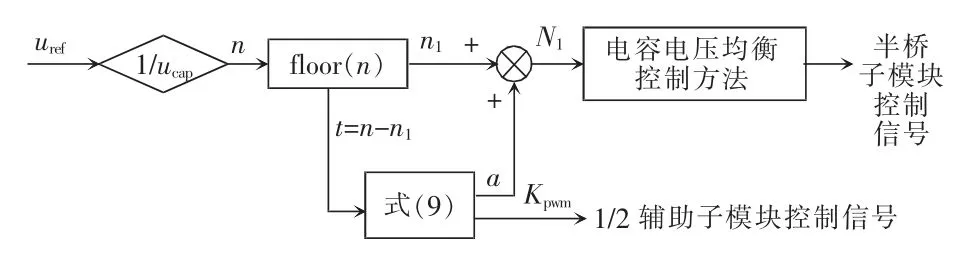
图4 改进型MMC 拓扑平衡控制Fig.4 Topology of improved MMC under balance control

（1）如果t=0，说明此时不需要投入全桥子模块，只需根据NLM 调制方式直接投入半桥子模块；

（2）如果0＜t＜1，则需要根据差值t 的大小、电容的充放电特性以及桥臂电流的方向来进行全桥子模块的投切，具体方法如下。

以流过桥臂电流的方向为正，即i＞0 为例，假定需要额外投入的半桥子模块输出UC和0 时分别表示为“1”和“0”，1/2 辅助子模块的开关状态分别为“PWM”和“-PWM”。考虑桥臂电流i 的方向、投入个数的差值t 的取值范围，可以将1/2 辅助子模块的输出状态在表2 中表示出来，同理可以得到i＜0的情况。

表2 1/2 辅助子模块的输出状态Tab.2 Output status of 1/2 auxiliary sub-module

1）当0＜t≤1/2 时

此时全桥子模块需要投入的电压在0～UC/2 之间，而1/2 辅助子模块的电容电压为UC/2。因此，通过调节PWM 参考波的大小控制1/2 辅助子模块正向投入，即可输出这个范围的电压要求，不需额外引入未被投入的半桥子模块。此时，1/2 辅助子模块输出电压为

2）当1/2＜t＜1 时

此时全桥子模块需要投入的电压在UC/2～UC之间，而1/2 辅助子模块的电容电压为UC/2。因此，只通过正向投入1/2 辅助子模块无法输出这个范围的电压要求，需额外引入未被投入的半桥子模块。为了使半桥和全桥子模块之间的电容电压保持均衡，额外引入1 个半桥子模块后，1/2 辅助子模块需要反向投入。此时，额外投入的半桥子模块和1/2辅助子模块等效输出电压为：

式中，up为额外引入的半桥子模块的输出电压。

由于电容的充放电特性，半桥子模块和1/2 辅助子模块的电容电压一直处于波动状态，上述控制策略并不能完全保证1/2 辅助子模块充放电平衡。为了实现1/2 辅助子模块的平衡控制，使得1/2 辅助子模块电容电压维持在UC/2 附近，可以通过调节1/2 辅助子模块的调制信号来实现，该调节量大小记为m。调节量m 的大小需要考虑每一时刻1/2 辅助子模块的电容电压实际值和标称值之间的大小关系以及上、下桥臂电流的方向，即根据当前1/2 辅助子模块对充放电的需求来决定调节量m 的正负。

生成1/2 辅助子模块调制信号调节量m 的控制框图如图5 所示，调节量m 的生成采用滞环控制。将调节量m 加入即可得到上、下桥臂1/2 辅助子模块的调制信号。然后将得到的调制信号和三角载波进行比较即可生成上、下桥臂1/2 辅助子模块的PWM 控制信号，通过该方法可以使得1/2 辅助子模块的电容电压维持在UC/2 附近。

图5 1/2 辅助子模块调制信号生成框图Fig.5 Block diagram of 1/2 auxiliary sub-module modulation signal generation

图5 中，vHp1和vHn1表示每一时刻上、下桥臂1/2辅助子模块电容电压的实际值。以上桥臂1/2 辅助子模块为例，uHp1和vHp1的关系可表示为

式中，S 为上桥臂1/2 辅助子模块的开关函数。

3.3 1/2 辅助子模块的降频策略

根据上一节1/2 辅助子模块的平衡控制策略可知，在上、下桥臂半桥子模块投入或者切除的每一瞬间，都需要1/2 辅助子模块正向或者反向参与电容电压的均衡，这样可以最大程度降低MMC 系统输出电流的谐波畸变率。但是由于1/2 辅助子模块采用的是载波控制，这就使得其开关频率会非常高。而开关频率的增加不但对开关器件的要求会大幅提高，而且还会造成较大的开关损耗，降低系统的输出效率。

由上述分析可知，系统输出电流的谐波畸变率和1/2 辅助子模块的开关频率存在矛盾。因此，研究两者之间的关系，在保证MMC 输出电流谐波畸变率满足需求的同时，尽可能的减小1/2 辅助子模块的开关频率，对串联全桥子模块的MMC 系统是必要的。

图6（a）所示为调制度m=0.8，1/2 辅助子模块全部投入时，半桥投入子模块个数和控制全桥子模块通断的PWM 信号之和的理论图。根据图6 可以看出，由于加入了1/2 辅助子模块，MMC 输出电流的电平数会增加，谐波畸变率会随之降低，但由于在每个电平跳变时，1/2 辅助子模块都会一直投切，其开关频率会非常高。

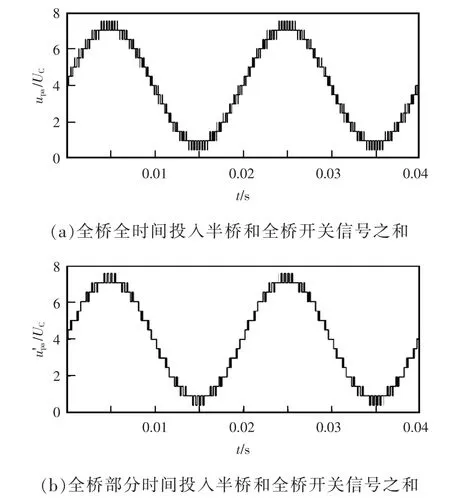
图6 改进前后半桥和全桥开关信号之和理论Fig.6 Improved theoretical diagram of sum of front and rear half bridge and full bridge switch signals

图6（b）所示为调制度m=0.8，1/2 辅助子模块部分投入时，半桥投入子模块个数和控制全桥子模块通断的PWM 信号之和的理论图。与图6（a）1/2辅助子模块完全投入时相比，虽然输出电流的谐波畸变率有所增加，但是1/2 辅助子模块的开关频率大幅度的降低。

4 仿真分析

为验证本文所提出的改进MMC 拓扑和控制方法的可行性和有效性，在MATLAB/Simulink 仿真平台上搭建三相MMC 仿真，仿真参数如表3 所示。

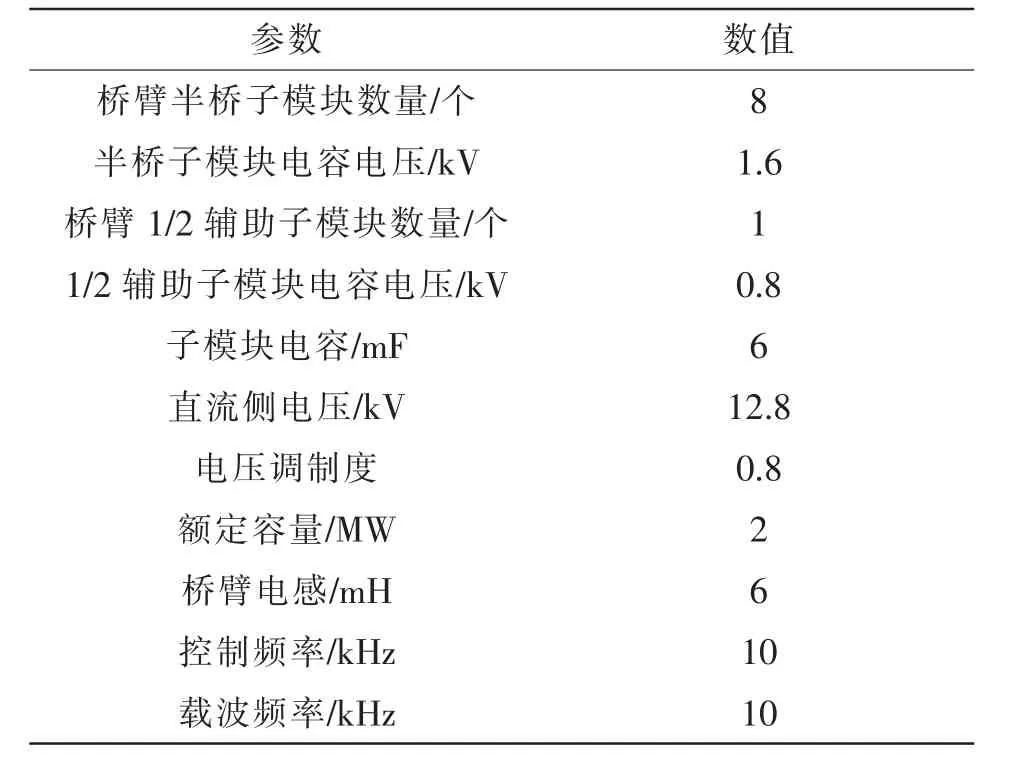
表3 仿真参数Tab.3 Simulation parameters

在半桥子模块每次投切过程中，投入全桥子模块的时间占比从0～100%变化时，MMC 输出电流的谐波畸变率和全桥器件的平均开关频率之间的关系如图7 所示。其中，电流THD 与平均开关频率关系是通过仿真结果描点得到。可以看出，随着全桥子模块投入时间占比的提高，MMC 输出电流的谐波畸变率会逐渐降低，但全桥器件的平均开关频率也在大幅提高。图8 所示为传统NLM 控制方法下，MMC 交流侧输出电流波形、谐波频谱图和A 相上桥臂电容电压的波形。根据仿真结果可知，基波幅值为508.5 A，总谐波畸变率为6.15%，子模块电容电压在1 600 V 附近波动。

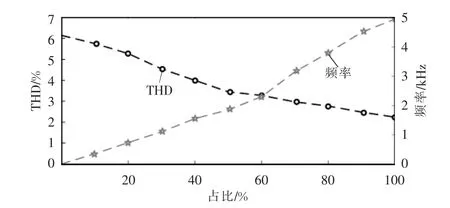
图7 全桥不同投入时间下输出电流THD 和全桥器件的平均开关频率Fig.7 Output current THD and average switching frequency of full-bridge sub-module under different operation time of full-bridge

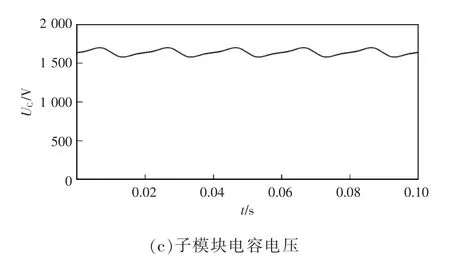
图8 传统NLM 调制仿真结果Fig.8 Simulation results under traditional NLM modulation

以全桥子模块投入时间的占比为50%为例，全桥子模块仅在0.25＜t＜0.75 时投入，仿真结果如图9所示。根据仿真结果可知，基波幅值为507.7A，总谐波畸变率为3.50%，相比于传统MMC 降低了43%，半桥子模块电容电压在1 600 V 附近波动，全桥子模块电容电压在800 V 附近波动。全桥子模块投入时间的占比为50%时，其器件的开关频率约为1.85 kHz；全时间投入时，其器件的开关频率约为4.95 kHz，全时间投入时其子模块相比于全桥全时间投入降低了63%。

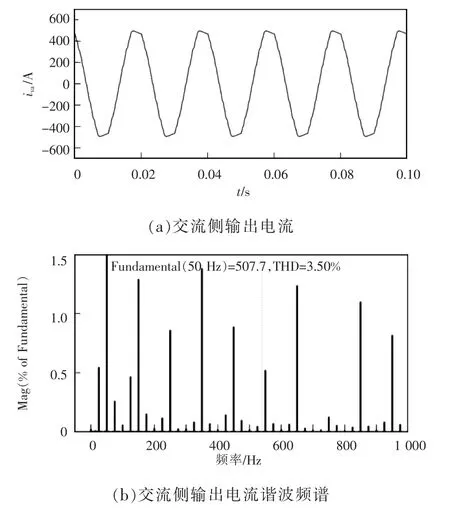
图9 改进混合调制策略仿真结果Fig.9 Simulation results under improved hybrid modulation strategy

为了验证所提混合调制策略在动态工况下的性能，系统在交流侧接10 Ω 负载电阻达到稳定后，在1s 时，负载电阻突然由10 Ω 增加到20 Ω，以考察系统的动态性能。采用传统控制方法，MMC 输出波形如图10（a）所示。从图中可以看出，稳定后输出电流的基波幅值为254.3 A，谐波畸变率为8.21%，子模块电容电压在1 600 V 附近波动。采用改进后的混合调制策略，MMC 输出波形如图10（b）所示。

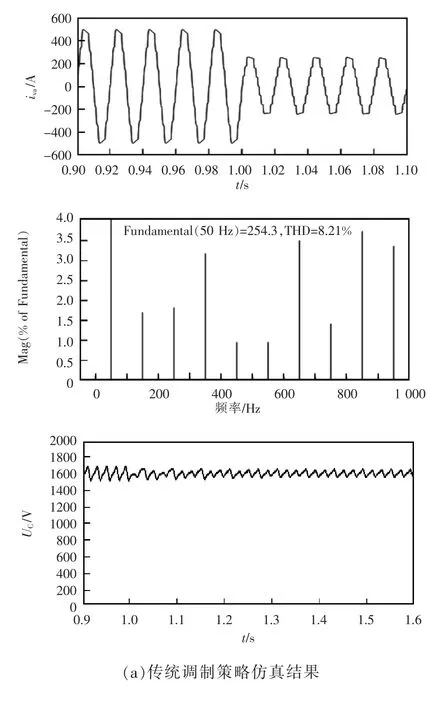
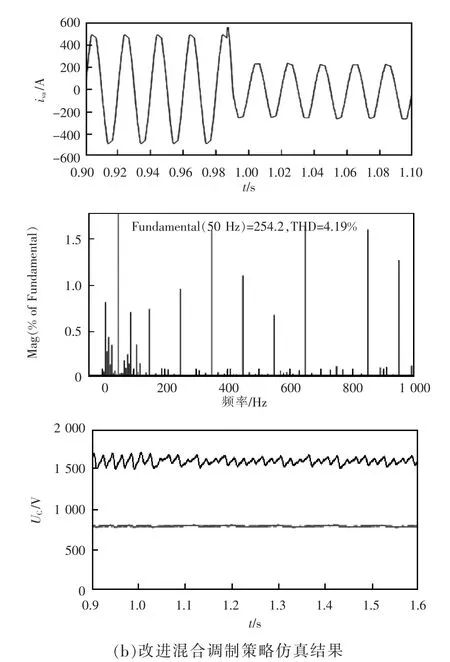
图10 变负载情况下改进前后调制策略仿真结果Fig.10 Simulation results before and after improved modulation strategy under variable load

从图中可以看出，稳定后输出电流的基波幅值为254.2 A，谐波畸变率为4.19%，半桥子模块电容电压在1 600 V 附近波动，全桥子模块电容电压在800 V 附近波动。因此，本文所提改进混合调制策略在变功率情况下仍旧适用。

根据仿真结果可以得到，本文提出的改进混合调制策略在电流畸变率和子模块电容电压方面优于传统NLM 控制方法，全桥器件的开关频率低于全桥子模块全时间投入时的器件的开关频率，仿真验证了本文所提控制方法的有效性。

5 结论

为了解决子模块数较少情况下，NLM 调制方式存在的电流谐波畸变率较大的问题，本文设计了一种在传统半桥MMC 每个桥臂串联1 个全桥子模块的拓扑，并针对这种MMC 拓扑提出了一种改进的混合调制策略，可以有效降低系统的谐波畸变率。通过分析输出电流谐波畸变率和1/2 辅助子模块的动态关系，给出了一种降低全桥子模块开关频率的方法。

考虑该MMC 拓扑在正常运行状态下，半桥和全桥子模块电容电压之间的差异，在调制策略中对1/2辅助子模块加入一个调节量，进一步对全桥子模块电容电压进行均衡控制，提高了输出电流的质量。

最后，在Matlab/Simulink 中搭建了本文MMC拓扑的仿真模型，并对本文提出的混合调制策略进行了验证，证明了本文提出的混合调制策略和电容电压均衡控制策略的可行性和有效性。