湍流信道中零填充三模光正交频分复用索引调制的性能分析

周伟煜,王惠琴,王 真,唐崎涵,张留堡,朱建梅

( 兰州理工大学 计算机与通信学院,兰州 730050)

0 引 言

索引调制(index modulation,IM)在不消耗额外能量的情况下,可利用天线、时隙、弥散矩阵和子载波[1]等额外传递信息。鉴于此,学者们将正交频分复用(orthogonal frequency division multiplexing,OFDM)与IM相结合,提出了正交频分复用索引调制(OFDM with IM,OFDM-IM)。OFDM-IM利用激活子载波索引携带额外信息,因而获得了更高的传输速率和频谱效率(spectral efficiency,SE)。同时,也因静默子载波的存在有效消除了载波间干扰、降低了峰均比(peak-to-average power ratio,PAPR),从而大幅降低了系统的误码率(bit error rate,BER)。目前,OFDM-IM凭借上述优点,已成为无线通信领域中的研究热点之一。

E. Basar等[2]于2015年首次将索引调制技术用于光OFDM(optical OFDM,OOFDM),并提出了OOFDM-IM技术。该技术为解决现有无线光通信(optical wireless communication,OWC)技术难以满足未来高传输速率的要求提供了新的解决思路。目前有关OOFDM-IM的研究主要集中在发端方案的构造上[3-5]。其中,文献[3]将索引调制与星座模式相结合,构建了双模OOFDM-IM(dual-mode OOFDM-IM,DM-OOFDM-IM),该技术利用2种不同的星座模式实现了传输速率的提升;为了进一步提高系统传输速率,文献[4]通过构建实值虚拟子载波,提出了增强型DM-OOFDM-IM,该技术通过扩展索引比特有效地提高了传输速率和能量效率;文献[5]利用离散哈特莱变换代替傅里叶变换,有效提高了传输速率。上述方案通过不同的方式提升了传输速率,但均以牺牲误码率为代价。

本文通过在不同激活子载波上加载不同模式的星座符号的方式,并结合小波变换提出了一种零填充三模OOFDM-IM(zeropadded tri-mode OFDM-IM,ZTM-OOFDM-IM)系统,进一步提升系统的传输速率和误码性能。

1 系统模型

传统的DM-OOFDM-IM通过在子载波上传输2种不同模式的星座符号,实现了传输速率的有效提高。同时,也因所有载波被激活导致误码性能不理想。为了弥补DM-OOFDM-IM的不足,本文通过在激活子载波上加载2种不同的星座模式,而其他子载波保持静默(即零模式)的方式,提出了一种ZTM-OOFDM-IM技术。3种模式的存在提高了系统的传输速率,同时静默子载波的存在还能够有效降低系统的BER。ZTM-OOFDM-IM系统模型如图1所示。

图1 ZTM-OOFDM-IM系统模型Fig.1 ZTM-OOFDM-IM system model

图1中,发端先将输入的信息流分为G组。假设每组包含R比特信息,对每组信息进行二次分割,即将R分为索引比特R1和星座符号比特R2。其中,R1被用来选择激活子载波以及加载在激活子载波上星座符号的映射顺序,R2被映射为2种不同星座模式的调制符号。之后,将调制符号加载在激活子载波上,再经OFDM数据块合并、逆离散小波变换、并串变换等处理后由光源发送出去。经大气湍流信道传输的光信号由探测器接收,通过离散小波变换以及最大似然检测等处理后,即可恢复为原始信号。下面将详细描述信号的处理过程。

1.1 系统传输速率

(1)

因此,ZTM-OOFDM-IM系统所对应的传输速率为

(2)

相应的SE为

(3)

为了更直观地说明ZTM-OOFDM-IM系统带来的优势,表1给出了其与传统系统频谱效率的对比。其中,ACO-OFDM表示非对称限幅光OFDM (asymmetrically clipped optical,ACO-OFDM),为了便于对比,所有系统均不考虑循环前缀。由表1可见,相较于传统系统,所提方案大幅提升了系统的传输速率及频谱效率。

表1 不同系统的频谱效率

1.2 信号的映射与解映射

(4)

下面以MA=2、MB=4、l=4、k1=k2=1为例来说明系统的映射规则,其结果如表2所示。在完成信号映射之后,合并各子载波块上的信号并生成OFDM块。为了提高子载波利用率,同时增强子载波间的正交性,采用离散小波变换(discrete wavelet transform,DWT)[6]替换传统的傅里叶变换,将信号转换成适合激光器传输的信号。也就是说,利用逆DWT (inverse DWT,IDWT)将OFDM数据块中的复数信号转换为正实数信号,再经并串转换后由激光器发送至接收端。采用DWT不仅提高了子载波的利用率,还可以增强子载波间的正交特性,有效抵抗大气湍流的影响。

表2 系统的映射规则

假设接收端检测器接收到的信号为

y=ηhx+ω

(5)

(6)

(6)式中:Γ(·)表示Gamma函数;Kr(·)为修正的第二类r阶贝塞尔函数r=a-b,a和b分别为大尺度和小尺度散射系数,它们与大气折射率结构常数、波长、空间波数、光束传输距离以及接收孔径的大小有关,具体关系见文献[8]。

光电探测器接收的信号经DWT后,可采用最大似然估计(maximum-likelihood,ML)来完成激活子载波索引、星座模式顺序和星座调制符号的检测。其准则为

(7)

2 系统误码率分析

下面以激活2个子载波,调制阶数M=MA=MB为例,详细推导ML检测时ZTM-OOFDM-IM系统的误码率。依据文献[9],采用联合界技术时,ZTM-OOFDM-IM系统平均比特错误概率(average bit error probability,ABEP)的上界可表示为

(8)

(9)

(10)

由(10)式可见,获得ABEP的关键是正确分析检测错误的类型,并计算出其对应的APEP。只有当激活子载波索引、星座映射顺序和QAM调制符号均被正确检出时,信号才能被正确解调。因此,综合考虑影响系统误码性能的因素,其错误可归纳为以下7类。

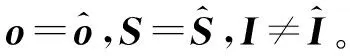
由于激活了2个子载波,因此,第1类错误中的索引错误有3种情况,即第1、2位索引均错,第1或第2位索引单独错误,可表示为

(11)

(12)

第2类、第6类和第7类错误可参照第1类错误的分析方法,其结果可表示为

W2=W7=3s2h2

(13)

(14)

其错误分别包含M(M-1)k、M(M-1)k(k-1)和M(M-1)k项。

第3类错误可以表示为

(15)

其错误结果可表示为

W3=s2h2

(16)

其错误共包含有Mk项。采用同样的分析方法,第4类和第5类的错误可以表示为

(17)

(18)

其错误分别有Mk、Mk(k-1)和M(M-1)k项。

由上述可见,其错误类型表达式包含有h加权平方累加和以及h加权差的平方累加和形式。对于第1种形式,由于h是服从G-G分布的随机变量,其平方的矩量母函数(moment generating function,MGF)[10]为

(19)

(19)式中,G[·]为Meijer G函数。令PW1=PW1_1+PW1_2,根据有关多个随机变量MGF的性质[10],可求得W1_1的APEP为

(20)

(20)式中,c1=c2=2s2。对于错误类型W1_2,由于采用慢衰落信道,因此,在一个载波内信道系数相同,可以忽略其影响。

使用MGF方法可求得错误类型W2、W3和W7的APEP为

(21)

(21)式的PW2、PW3中代入c=3s2,PW7中代入c=s2,即可得到上述3类错误的平均成对错误概率。错误类型W4、W5的APEP同样可以忽略计算。

同样,对W6采用MGF方法,可计算出(14)式中的APEP,因此,第6类错误类型可表示为

(22)

将上述错误类型对应的APEP代入(8)式,即可得到系统的APEP为

M(M-1)kPW2+MkPW3+Mk(k-1)PW4+M(M-1)kPW5+M(M-1)k(k-1)PW6+M(M-1)kPW7]

(23)

由(23)式可知,系统的理论误比特率会受到调制阶数、激活子载波数目、子载波索引以及大气湍流强度等的影响,其具体影响将在下文中详细分析。

3 系统性能的仿真分析

表3 湍流模型参数

图2 不同湍流下ZTM-OOFDM-IM (4,2,1,4,4)系统的理论与仿真误码率Fig.2 Theoretical and simulated BER of ZTM-OOFDM-IM(4,2,1,4,4) systems with different turbulences

3.1 ZTM-OOFDM-IM系统的误码率分析

图2为不同湍流时ZTM-OOFDM-IM (4,2,1,4,4)系统的理论与仿真误码率。由图2可见:①随着信噪比的提高,理论与仿真BER性能逐渐靠近,且仿真结果与理论上的边界重合;②随着湍流强度的增大,系统的误码率性能会随之下降;③相比于仅有高斯白噪声的信道,湍流信道对系统误码率影响比较严重,尤其是中、强湍流。

图3为子载波块长度与激活子载波数对系统误码率的影响。由图3可见:①当子载波块长度固定时,增加激活子载波数可以大幅提升传输速率和SE,但会造成BER损失。例如,相比于(4,2,1,2,4)系统,(4,3,2,2,4)和(4,3,1,2,4)系统的传输速率分别提升了1和2 bpcu,频谱效率分别提升了16.7%和33.3%,而其信噪比在BER=10-3时,分别损失了约1.8和2 dB。②当激活子载波数量相同时,子载波块长度的增加会带来BER改善。例如,相比于(4,2,1,2,4)系统,(8,2,1,2,4)系统的信噪比在BER=10-3时提升了约2 dB。因此,本系统可以在传输速率与BER之间做出灵活的选择。

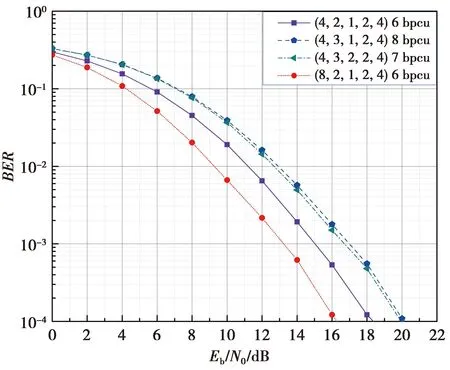
图3 子载波块长度与激活子载波数对系统误码率的影响Fig.3 Effect of subcarrier block length and number of activated subcarriers on system BER

图4为调制阶数对ZTM-OOFDM-IM系统误码率的影响。从图4可以看出:①随着调制阶数的增加,会带来传输速率的提升,但会损失一部分系统的误码性能。例如,在BER=10-3时,相较于M=4的系统,M分别为6、6、8和12时,系统的信噪比分别损失了约2、2、3和5 dB。而此时其对应的传输速率分别为5、6、6、7和8 bpcu。②当传输2种星座模式的激活子载波数相同时,星座模式顺序对系统的误码性能几乎没有影响。

3.2 不同系统误码率的对比分析

图5为OOFDM-IM、DM-OOFDM-IM和ZTM-OOFDM-IM系统的误码率。此时,所有系统子载波块长度均为4,且各激活2个子载波。由图5可见,在相同调制阶数下,ZTM-OOFDM-IM系统的误码率性能最佳。相较于OOFDM-IM和DM-OOFDM-IM系统,在BER=10-3时,ZTM-OOFDM-IM系统的信噪比分别提升了约2.8和3.2 dB。这是因为ZTM-OOFDM-IM系统降低了相邻子载波被同时激活的概率。

图5 OOFDM-IM、DM-OOFDM-IM和ZTM-OOFDM-IM系统的误码率Fig.5 BER of OOFDM-IM, DM-OOFDM-IM and ZTM-OOFDM-IM systems

4 结束语

为了解决传统无线光通信系统难以满足未来传输对速率和误码性能的高要求,本文提出了一种ZTM-OOFDM-IM系统。该系统通过子载波索引以及星座映射顺序来额外增加索引信息,实现了传输速率的有效提升,同时,通过静默子载波有效降低了误码率;利用仿真实验研究了湍流强度、激活子载波数、子载波块长度以及调制阶数对系统传输速率和误码率的影响,并与OOFDM-IM和DM-OOFDM-IM系统进行了对比。结果表明,ZTM-OOFDM-IM系统在保证传输速率的条件下,取得了较好的误码性能。虽然该系统获得了较好的性能,但因额外检测星座映射顺序而增大了ML算法的复杂度。因此,为了加速该技术的推广和应用,下一步将着重研究增强系统性能以及降低译码复杂度的有效方法。