基于压缩感知的可见光通信定位一体化系统性能分析
2024-02-26左洵赫王子雄于晋龙
左洵赫,王子雄,马 闯,于晋龙,江 阳
(1.天津大学 电气自动化与信息工程学院,天津 300072;2.贵州大学 物理学院,贵阳 550025)
0 引 言
随着科技的不断进步以及人们生活水平的改善,定位服务在日常生产生活中的应用越来越广泛[1]。传统的全球定位系统(global positioning system,GPS)在室外能够提供相当高的定位精度,但在室内环境中,信号在穿透建筑物时会发生衰减,从而导致系统定位精度的急剧下降[2]。因此,一些室内定位技术被提出,包括蓝牙、射频识别以及无线局域网等[3],它们都以电磁波作为传递信息的载体,一方面,可能会导致信息泄露,在一些对射频信号敏感的场景下,还可能会对人体或仪器设备造成一定的伤害;另一方面,发光二极管(light emitting diode,LED)技术趋于成熟,促进了可见光通信(visible light communication,VLC)技术的产生。VLC技术利用LED发出人眼无法察觉到的快速闪烁光信号传递信息,在充当照明设备的同时提供了通信服务,既降低了系统成本,又能够在封闭空间内有效保证传输信息的安全性[4]。近几年,随着VLC技术的快速发展,基于可见光通信的可见光定位(visible light positioning,VLP)技术逐渐成为室内定位的热门方案[5]。在可见光定位的传输信道中,接收成分主要以视距成分的光信号为主,降低了多径干扰对定位算法的影响,从而使可见光定位方案获得了较其他传统室内定位方案更高的定位精度[6]。
现有的可见光定位算法主要包括接收信号强度算法(received signal strength,RSS)、到达时间算法(time of arrival,TOA)、到达时间差算法(time difference of arrival,TDOA)、到达相位差算法(phase difference of arrival,PDOA)以及到达角度算法(angle of arrival,AOA)等[7]。其中,TOA定位算法首先在发射端与接收端之间利用原子钟精确同步,测量发射端的定位信号到达接收端时的时间传播延迟,然后计算发射端与接收端之间的距离,最后通过最小二乘法根据3个或3个以上的距离信息定位接收端的位置[8]。在室内定位中,由于发射端和接收端之间的距离通常较近,因而信号的传播时间较短,这就要求TOA定位算法中的接收端具备相当高的信号采样率,从而准确地估计接收信号的时间延迟。然而,随着信号采样率的增加,系统的部署成本也会增加,这使得TOA定位技术难以大范围应用[9]。
压缩感知算法提供了在远低于奈奎斯特采样率的条件下恢复原始信号的可能[10]。压缩感知算法是一种非线性重构算法,通过不等间距采样获得原始信号的离散测量样本,再利用信号重构算法恢复原始稀疏信号或原始信号的稀疏表示[11]。在过去的研究中,已有一些压缩感知算法在可见光通信领域中应用。文献[12]中,接收机只能接收到相邻区域内有限数量的发射端发来的信号,因此,接收信号具有自然稀疏性,作者利用压缩感知算法重构了房间内其他区域中发射端的信号,从而获得了更多的定位信息,由于参考位置数量的增加,因此提高了系统的定位精度。文献[13]中,作者提出了一种反向定位系统,定位目标作为发射端携带LED,天花板上放置多个光电二极管(photo diode,PD)接收来自发射端的信号,作者通过将目标定位问题转换为稀疏位置信息矩阵重构问题,并利用压缩感知算法降低了定位误差。2种方案都利用压缩感知算法重构可见光通信中的稀疏信号,但未能充分发挥压缩感知算法在信号处理上的重要作用。在基于正交频分复用(orthogonal frequency division multiplexing,OFDM)技术的可见光通信系统中,每个发射端的传输信号都只占据整个通信带宽中的一部分,信号满足频域上的稀疏性,这为在可见光通信中应用压缩感知算法进行信号处理提供了理论基础。
为了降低TOA定位算法对接收信号采样率的需求,本文提出了基于压缩感知的可见光通信定位一体化系统。系统采用OFDM通信技术和TOA定位技术相组合的方式,既实现了发射端与接收端的通信,又能准确估计收发端之间的距离。发射端通过OFDM技术将传输数据调制到不同的频带上并作为发射端的驱动信号。同时,不同的发射端也依次向接收端发送用以定位的导频信号。接收端将光信号转换为电信号后,通过带通滤波器将来自不同接收端的OFDM通信信号与TOA定位信号进行分离,并通过压缩感知算法进行信号重构,最终经过译码得到传输数据,通过测量峰值时间差计算收发端之间的估计距离。
1 系统模型
1.1 信道模型
本文提出的定位系统包括4个LED为发射机提供通信与照明功能,1个PD作为接收机接收来自LED的信号。LED被放置在天花板上关于中心对称,PD被放置在距离地面一定高度的某个位置上以模拟现实情况,系统模型如图1所示。

图1 系统模型Fig.1 System model
由于多径作用,可见光通信信道包括视距(light of sight,LOS)成分和非视距(non light of sight,NLOS)成分,而OFDM技术可以有效地对抗多径干扰[14],因此,本文仅考虑视距成分。根据朗伯模型,当PD的入射角小于视角时,从发射端到接收端信道增益的数学表达式为[15]
(1)
(1)式中:A是PD的有效面积;D是LED与PD之间的距离;φ和ψ分别是LED的发射角和PD的入射角;T(ψ)和g(ψ)分别是光滤波器的增益和聚光器的增益;m是朗伯系数,它的数学表达式为[16]
(2)
(2)式中,Φ1/2是LED的半功率角。假设发射信号为x(t),则接收信号y(t)的数学表达式可以表示为
y(t)=GLOSx(t)+n(t)
(3)
(3)式中,n(t)由散粒噪声和热噪声组成[17]。
1.2 TOA定位算法
由于光速恒定,光的传播距离与传播时间成正比,因此,在接收机和发射机精确同步后,可以通过测量信号发出到信号接收的传播延迟来计算发射机与接收机之间的距离。第i个发射机与接收机的距离di的数学表达式为
di=cτi
(4)
(4)式中:c表示光速;τi表示第i对收发端的总传播延迟,主要由2部分组成,其数学表达式为
τi=τLOS+τNLOS
(5)
(5)式中:τLOS表示LOS链路上的传播延迟;τNLOS表示NLOS链路引起的附加误差[18]。为了简化系统,本文仅考虑压缩感知算法对接收信号LOS链路上的传播延迟的重构。
在得到3个或3个以上的距离关系后,通过最小二乘法从发射机的已知位置推算接收机的未知位置,假设第i个发射机的坐标为(xi,yi,zi),接收机的坐标为(x0,y0,z0),根据三边定位法,接收机坐标、发射机坐标以及收发端之间距离的数学关系式为
(6)
当TOA定位系统采用导频信号作为定位信号时,在不考虑噪声的情况下,发射信号x(t)与接收信号y(t)如图2所示,其数学表达式为[19]
(7)

图2 TOA算法中的发射信号与接收信号Fig.2 Transmitted and received signals in TOA algorithm
(7)式中:K为发射信号的峰值;fc为导频。
从图2可以看出,2种信号达到峰值的时间差为1 ns,则可以认为传播延迟为1 ns,因此,计算得到发射机与接收机的距离为0.3 m。此时,接收机的采样率至少为1 GHz才能采集到准确的峰值信息,即TOA定位算法的定位精度由系统采样率决定。假设想要获得至少3 cm的定位精度,则系统至少需要10 GHz的信号采样率,这会增加系统的部署成本。
本文采用基于导频信号的TOA定位算法,假设发射机与接收机之间已经精确同步,4个发射机依次向接收机发送导频信号,接收机依次测量导频信号的传播延迟,从而获得接收机与4个发射机的距离信息,最终得到接收机的估计位置。值得注意的是,4个发射机依次发送信号的时间间隔不宜太短,以防止相互干扰。
1.3 基于OFDM的通信定位一体化系统
OFDM技术能够在一定带宽内同时实现VLC和VLP两种功能,频谱分配如图3所示。在发射端,整个带宽被划分成5个部分,包括4个LED与PD通信所用的频带以及用来确定收发端距离的定位导频。由于传输的光信号要求为正实数信号,因此,采用厄密特对称确保快速反傅里叶变换后LED的驱动信号是实数信号[20],并在其基础上加上一定的直流偏置信号以保证信号幅度始终为正。在接收端,PD将光信号转换为电信号,经过快速傅里叶变换(fast Fourier transform,FFT)后分析接收到的每一个LED各自所占频带的通信信息以及导频信号通过传播延迟传递的距离信息,最后计算一体化系统的误码率以及距离估计误差。

图3 基于OFDM的VLC和VLP系统的频谱分配Fig.3 Spectrum allocation of VLC and VLP system using OFDM
2 压缩感知算法的基本原理
压缩感知算法是利用先验信息在某个变换域上的稀疏性,通过远低于奈奎斯特采样定理要求的采样点数重建原始信号的方法,能准确恢复信号的两个原则是原始信号或其稀疏表示的稀疏性以及测量矩阵与稀疏正交基的不相关性[21]。假设原始信号x是长度为N的一维离散信号,则可以用一组标准正交基Ψ={φ1,φ2,…,φN}的线性组合来表示原始信号x,其数学表达式为
(8)
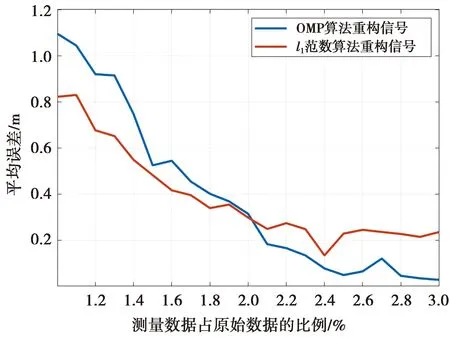
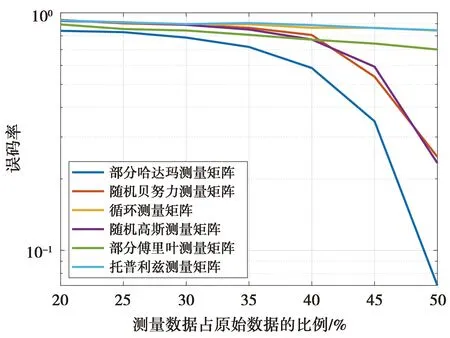
(8)式中:θi是原始信号x在正交基φi方向上的投影系数,假设向量θ中含有K个非零元素,则向量θ称为K稀疏的投影稀疏向量;Ψ也可称为原始信号x的稀疏矩阵。如果将原始信号x投影至与稀疏矩阵Ψ不相关的M×N(M< y=Φx (9) (9)式中,测量信号y是长度为M的一维离散信号。结合(8)式—(9)式可以进一步表示为 y=ΦΨθ=Θθ (10) (10)式中,Θ=ΦΨ是感知矩阵。为了求解稀疏向量θ,在一定条件下,可以将(10)式转换为最优化问题[23] min‖θ‖0s.t.y=ΦΨθ (11) (11)式中,‖·‖0表示l0范数。 压缩感知算法主要由信号稀疏表示、压缩测量矩阵以及信号重构算法3部分内容构成。通常情况下,原始信号x是非稀疏的,因此,需要选取合适的正交基Ψ对原始信号进行稀疏表示,常用的稀疏表示基包括傅里叶基、离散余弦基以及小波基等。 为了选取适合的测量矩阵确保与稀疏矩阵的不相关性[24],需要确定感知矩阵是否满足约束等距性(restricted isometry property,RIP)条件,常见的测量矩阵包括部分哈达玛矩阵、高斯随机矩阵、局部傅里叶矩阵以及稀疏随机测量矩阵等。 常见的信号重构算法包括凸松弛算法和贪婪算法两类[25]。当感知矩阵满足RIP条件时,l0范数优化问题与l1范数优化问题具有相同的解,凸松弛算法将l0范数最优化问题转换为l1范数最优化问题,虽然运算过程复杂,但算法精度高;贪婪算法的代表之一是正交匹配追踪(orthogonal matching pursuit,OMP)算法,其主要特点是运算速度快、算法复杂度低。 为了降低TOA定位算法中对接收信号采样率的需求,从而减少系统的部署成本,本文提出了基于压缩感知的可见光通信定位一体化系统,系统框图如图4所示。在发射端,通信部分通过OFDM技术将传输信息利用快速反傅里叶变换调制到不同的频带上作为每个LED的驱动信号,定位算法通过导频信号依次驱动LED发出定位信号并测量系统中的TOA信息来估计LED与PD的距离。在接收端,PD首先将接收到的光信号转换为电信号,通过5个带通滤波器分别将来自4个LED的OFDM通信信号与来自某一个LED的导频定位信号分离,然后利用压缩感知算法采集少量测量数据进行信号重构,最后对重构后的OFDM信号进行FFT,并译码为二进制比特数据从而计算误码率;重构后的导频信号通过收发端的同步得到接收信号的绝对时间信息,从而计算发射信号与接收信号的峰值时间差即传播延迟,以此计算出各个LED与PD的距离。 图4 基于压缩感知的可见光通信定位一体化系统的系统框图Fig.4 System block diagram of an integrated system for visible light communication and positioning based on compressed sensing 本文采用MATLAB软件仿真平台构建了一个OFDM仿真系统以验证本文所提出的一体化系统,系统部分参数如表1所示。 表1 仿真设置的系统参数 系统的整个带宽共分为128个子载波,直流分量为0,奈奎斯特分量作为导频子载波,其余126个子载波为信息子载波,均匀分给每一个LED,其中,LED1、LED2以及LED3各自占据32个子载波,而LED4占据30个子载波。导频信号频率为50 MHz,正交基选择为FFT变换基,测量矩阵选择为部分哈达玛矩阵。仿真系统的房间大小为8 m×8 m×6 m,其中,包括4个LED与1个PD,LED关于天花板中心对称,距离中心2.83 m,它们的坐标分别为(-2,-2,6)、(-2,2,6)、(2,-2,6)以及(2,2,6),单位为米。PD放置在房间的地面中心高0.8 m的位置,坐标为(0,0,0.8),单位为米。发射机与接收机之间精确同步,4个LED依次发送导频信号以标识身份,导频信号每次在一个LED上持续驱动1.28 μs,间隔时间为5 μs。由于驱动LED1的OFDM信号的最高频率高于其他LED的驱动信号,因此,接下来的仿真均针对于LED1的发射信号进行误码率仿真和收发端距离的估计仿真。为了得到插值重建后更高频率的离散原始信号以仿真压缩感知算法,且更有利于在模拟过程中重构峰值信息,分别选择100 MHz和800 MHz作为通信系统和定位系统的原始采样频率。 本节探究了重构算法与测量数据比例对一体化系统定位性能的影响。当原始信号的采样频率为800 MHz时,取原始采样数据的1.0%作为测量数据,采用l1范数算法以及OMP算法重构的信号如图5所示。可以看出,虽然OMP算法的重构信号更加平滑,但在20 ns和40 ns时刻,l1范数算法重构信号的峰值时间都比OMP算法重构信号更接近真实的峰值时间,l1范数算法的峰值时间平均误差为0.125 ns,OMP算法的峰值时间平均误差为1.25 ns。 图5 不同重构算法下的重构信号与原始信号Fig.5 Reconstructed signal and original signal under different reconstruction algorithms 其他条件不变,取1 000个峰值时间差计算平均误差,2种算法下,不同测量数据比例的平均误差如图6所示。随着测量数据比例的增加,2种信号重构算法的平均误差都逐渐降低,同时,l1范数重构算法始终优于OMP算法,当测量数据占原始800 MHz采样信号的2.1%时,l1范数算法的平均误差下降至0,为采样定理所需点数要求的16.8%;OMP算法的平均误差下降至0时,测量数据比例则增加到2.6%,为采样定理所需点数要求的20.8%。 图6 不同测量数据比例下定位系统的平均误差Fig.6 Average error for positioning system under different measurement data ratios 本节探究了重构算法与测量数据比例对一体化系统通信性能的影响。当原始信号的采样频率为100 MHz时,取原始信号的50%作为测量数据,通过l1范数算法以及OMP算法的重构信号如图7所示,OMP算法重构信号与L1范数算法重构信号对比的局部放大图也在图7中被标出。从图7可以看出,2种算法均能准确地重构原始信号。以重构信号幅度与原始信号幅度的标准差作为衡量算法重构程度的标准,经计算得到,l1范数算法重构信号幅度的标准差为2.49×10-8V,OMP算法重构信号幅度的标准差为1.86×10-21V,与原始信号十分接近。因此,在测量数据量占原始采样数据量一半的情况下,OMP算法的性能优于l1范数算法的性能。当原始数据采样率为100 MHz,即奈奎斯特采样率时,传输100帧数据并计算误码率,每一帧包含16 bit,共1 600 bit,2种算法在不同测量数据占原始数据比例下的误码率如图8所示。从图8可以看出,在测量数据比例小于45%时,OMP算法始终优于l1范数算法,在测量数据比例继续增加时,2种算法的误码率都迅速下降,在测量数据比例大于60%时,2种算法的误码率均下降到10-3以下。 图7 不同重构算法下的重构信号与原始信号Fig.7 Reconstructed signal and original signal under different reconstruction algorithms 图8 不同测量数据比例下通信系统的误码率Fig.8 Bit error rate for communication system under different measurement data ratios 为了探究噪声对一体化系统性能的影响,在其他条件不变的情况下,本文对加入噪声后的一体化系统进行了仿真,噪声参数如表2所示。 表2 仿真系统的噪声参数 保持原始信号采样率800 MHz不变,不同测量数据比例下定位系统的平均误差如图9所示。从图9可以看出,噪声存在时,定位系统的平均误差普遍高于图6中的平均误差,这是由于噪声会导致定位系统错误判断峰值时间,从而引起定位误差的增加。同时,在测量数据比例上升时,OMP算法的定位精度逐渐超过l1范数算法,这说明OMP算法在重构原始信号时拥有比l1范数算法更高的对抗噪声干扰的能力。然而,在测量数据比例达到3%时,平均误差仍未达到0,这说明需要通过进一步增加导频信号功率来提高系统信噪比水平,从而获得更好的定位结果。 图9 不同测量数据比例下定位系统的平均误差Fig.9 Average error for positioning system under different measurement data 保持原始信号采样率100 MHz不变,不同测量数据比例下通信系统的误码率如图10所示。在测量数据比例小于45%时,OMP算法相较于l1范数算法能够更好地从噪声中重构OFDM通信信号,并获得更低的误码率,但随着测量数据比例的增加,l1范数算法的高精度特点逐渐显现,在测量数据比例占75%时,l1范数算法的误码率降低到10-3以下,而OMP算法的误码率仅低于10-2。在当前的噪声水平下,虽然测量数据比例较没有噪声时的测量数据比例增加了15%,但压缩感知算法所需的测量数据量仍少于采样定理所需的采样率100 MHz时的测量数据量。 图10 不同测量数据比例下通信系统的误码率Fig.10 Bit error rate for communication system under different measurement data ratios 因此,对于一体化系统,在提高传输信号功率以改善信噪比的同时,也需要适当提高一体化系统的采样率以适应不同的工作环境,在实际应用中,采用相对较高的测量数据量是必要的,且不会造成系统性能的冗余。 本节探究了测量矩阵对一体化系统性能的影响。虽然部分哈达玛测量矩阵拥有良好的重构性能,但仍有许多满足RIP条件,即与大多数稀疏矩阵不相关的测量矩阵可以应用于压缩感知算法,因此,本节对比了随机高斯测量矩阵、随机贝努力测量矩阵、部分傅里叶测量矩阵、托普利兹测量矩阵以及循环测量矩阵在一体化系统中的性能表现,重构算法选择为OMP算法,稀疏基选择为FFT基。 保持原始信号采样率100 MHz不变,不同测量矩阵下通信系统的误码率如图11所示。从图11可以看出,在测量数据比例达到50%时,循环测量矩阵、托普利兹测量矩阵以及部分傅里叶测量矩阵都未能达到理想的误码率,误码率依然高于0.7;其余3种测量矩阵中,本文所提的压缩感知算法采用的部分哈达玛测量矩阵的误码率低于10-1,随机高斯测量矩阵和部分贝努力测量矩阵的误码率均在0.23左右。在整个测量数据比例中,本文所采用的部分哈达玛测量矩阵的精度均优于随机高斯测量矩阵、部分贝努力测量矩阵以及其他测量矩阵。 图11 不同测量矩阵下通信系统的误码率Fig.11 Bit error rate for communication system under different measurement matrices 本文为了降低TOA定位算法对信号采样率的需求,提出了基于压缩感知的可见光通信定位一体化系统。接收端利用带通滤波器分离不同频带下的通信信号与定位信号,以远低于奈奎斯特采样点数的不等间隔采样得到原始信号的离散数据,通过信号重构算法恢复原始信号,并计算误码率,进行距离估计得到平均误差。仿真结果表明,当通信系统误码率低于10-3时,压缩感知算法所需测量数据量为采样定理所需点数的60%;当定位系统能够准确估计收发端距离时,压缩感知算法所需测量数据量为采样定理所需点数的16.8%,仿真证明了压缩感知算法在一体化系统上的优越性,并且也证明了在本文所提出的工作环境下,部分哈达玛测量矩阵较其他测量矩阵对于后续重构信号有着更为积极的作用。此外,在引入噪声后,随着压缩感知算法对测量数据需求量的增加,也要求提高原始信号功率以改善信噪比情况。因此,在未来的工作中,针对低信噪比环境下的信号重构算法仍有很大的研究空间。3 基于压缩感知的定位算法

4 仿真分析
4.1 仿真设置

4.2 重构算法与测量数据比例对系统定位性能的影响


4.3 重构算法与测量数据比例对系统通信性能的影响


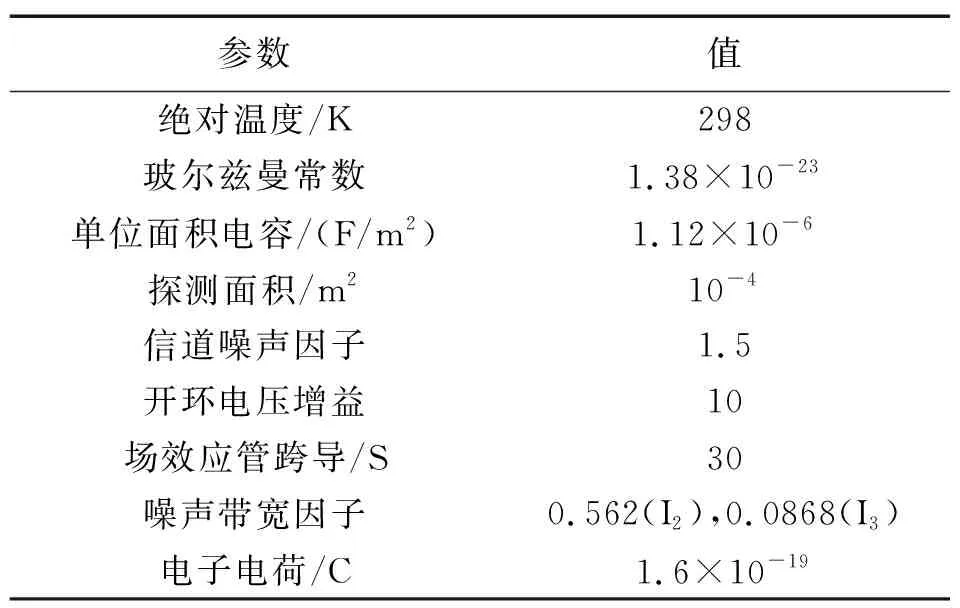
4.4 噪声对系统性能的影响

4.5 测量矩阵对系统性能的影响
5 结束语
