混合供能蜂窝网络的投资回报率和碳效联合优化

喻 越,闫 文,钟 祎,葛晓虎

(1.华中科技大学 电子信息与通信学院,武汉 430074;2.华为技术有限公司,上海 201206)

0 引 言

随着无线设备数量增加,无线业务流量随之增加,信息和通信技术行业逐渐成为引人注目的高能耗与高碳排行业。据估计,全球 2%～10% 的能源消耗、约 2% 的二氧化碳排放量是由信息和通信技术行业造成的,其中基站占总能源支出的60%～80%[1]。在“双碳”目标的驱动下,通信领域“5G基站+光伏+储能”的5G基站系统成为数字基础设施应用光伏供能的新方式[2]。但是此应用面临一定挑战。光伏发电具有间歇性、波动性及能流密度低等缺点,如果光伏储能系统规模过小,基站供能不足,那么会导致网络服务不稳定;但光伏储能系统规模过大,又会导致系统建设成本过高。那么在建设5G基站系统时,该如何布设光伏板容量和电池储能容量,才能在保证蜂窝网络服务质量的情况下,使得全系统经济性最佳呢?

对于此类问题,已有了不少研究。此类问题的优化目标主要在于经济性指标,比如系统单日运营费用等。一部分研究通过规划光伏容量优化经济性指标。文献[3]采用多目标粒子群算法优化设计分布式能源系统,优化目标为尽量减少系统运营费用和二氧化碳排放。针对光伏容量规划的研究,主要是在光伏并网场景中,以保证电能质量为前提,极大化光伏容量。另一部分研究通过规划电池储能容量优化经济性指标。文献[4]利用机会约束规划理论和蒙特卡洛模拟方法分析分布式电源,通过建立基站间非合作博弈模型,使用粒子群算法和内点法求解各个基站的电池储能容量配置和储能策略,使得系统单日费用最小。文献[5]在基于太阳能-光伏-功率共享的分布式储能系统中,通过遗传算法搜索其分布式电池的最佳容量以最小化能量损失。此外,也有研究同时规划光伏容量与储能容量以优化经济性指标。文献[6]提出了基于博弈论的微电网多智能体容量配置优化模型,以年利润函数为目标函数,通过粒子群算法优化求得光伏储能配置容量的博弈纳什均衡。文献[7]在独立微电网中优化光伏存储容量,基于此非线性规划优化问题,使用顺序二次规划法求解分布式资源最佳尺寸,以最小化微电网的年总能量损失和能源成本。文献[8]构建了5G基站光伏储能系统微电网,提出两层优化配置方法以解决光伏储能系统容量规划问题,内层优化考虑基站微网间的能量共享,以最小化微电网日常运营成本为目标确定光伏储能系统的经济调度策略;外层则以最小化微电网年平均综合成本为目标,最终采用CPLEX求解器和遗传算法求解此两层模型。

目前,部署光伏储能系统的蜂窝网络研究中,主要存在“在此场景下,研究主要考虑的是经济性成本影响,而没有考虑光伏引入对蜂窝网络性能的影响”的问题。针对此问题,本文做了以下研究及贡献。

1)在光伏与传统能源混合供能的蜂窝网络架构场景下,本文解决了混合供能蜂窝网络的双层优化问题。外层优化关注系统经济性,在满足光伏利用率的要求下,使得系统的投资回报率最大;内层优化关注蜂窝网络性能,在保证用户服务速率要求下,通过调整基站发射功率分配策略,使得网络逐小时碳排放效率最优。

2)本文采用基于模拟退火的粒子群算法求解外层优化模型,得到经济性最优的光伏板容量和电池储能容量配置;采用拉格朗日对偶分解方法求解内层模型,得到碳排放效率最大的基站功率分配策略。

3)本文通过对光伏储能系统配置可变的5G基站系统经济性分析,分别得出了系统投资回报率、碳效与系统的光伏板面积和电池储能容量的关系。仿真结果表明,使用本文提出的算法可使得全系统投资回报率达到380.3%,光伏利用率达到96.5%;其内层的碳效优化算法相较于注水算法降低了31.8%碳排放量。

1 系统模型

1.1 系统架构

本文考虑下行链路蜂窝网络,网络包括Nb个同构基站,表示为B={B1,B2,…,BNb}。由于基站可部署的光伏系统体量较小,基站自建项目发电难以百分之百地满足基站需求[2],因而每个基站均配备光伏供能系统和电池储能系统 (主电源),同时单向接入传统能源(备用电源)。基站系统除了基本的设备结构外,还包括智能能量管理单元(energy management unit,EMU),主要功能是负责光伏供能与传统能源供能切换、电池储能充放电调度等。光伏与传统能源混合供能的蜂窝网络系统架构如图1所示。图1中,左下角为混合供能的基站简化示意图。

图1 混合供能蜂窝网络系统架构图Fig.1 Architecture diagram of cellular networks with hybrid energy supply

1.2 蜂窝网络模型

假定区域内包括Nb个同构基站,每个基站配置K根天线,接入基站Bi的用户数量为Nu,i,其中i=1,…,Nb。针对基站用户通信的下行链路,基站Bi的信道矩阵Gi为

Gi=HiDi

(1)

(1)式中,Hi、Di计算式为

(2)

(3)

(2)—(3)式中:Gi∈K×1为信道矩阵;Hi∈K×Nu,i为信道小尺度衰落矩阵(服从瑞利分布);hi,j∈K×1为基站Bi与其通信用户Uj的信道小尺度衰落,j=1,…,Nu,i;Di∈Nu,i×1为基站与用户间路径损耗矩阵;di,j为基站Bi与用户Uj间距离;α为路径损耗指数。

本文假设基站应用大规模多路输入多路输出(massive multiple input multiple output,Massive MIMO)技术,并使用匹配滤波(matched filter,MF)预编码技术。文献[9]指出,随着基站天线数的增加,Massive MIMO系统使用匹配滤波预编码时,基站信道矩阵矢量趋于相互正交,MF预编码趋于最优,信号干扰被逐渐削减,甚至可被消除。故依据香农公式和文献[10],用户Uj接入基站Bi的信息接收速率Ri,j为

(4)

(4)式中:Wi,j、Ptx,i,j分别为基站Bi分配给用户Uj的带宽和发射功率;σ2为加性噪声功率。

由于蜂窝网络通信中下行链路流量远大于上行链路流量[11],因而本文考虑蜂窝网络性能时仅考虑下行链路。网络下行链路总速率为网络覆盖范围内满足通信服务质量要求的用户信息接收速率总和,网络下行链路总速率C为

(5)

基站能耗模型可用静态功耗和动态功耗之和表示[12],基站总功率Pbs为

(6)

(6)式中:ηbs是基站功率效率;Pstatic是基站静态功耗;Pt是基站总发射功率。基站Bi的总发射功率为

(7)

1.3 光伏供能模型

光伏供能系统由光伏电池板、光伏控制器等组成。光伏发电量主要取决于光伏电池板接收到的太阳辐射量。参考地球自转规律,本文使用正态分布函数拟合单日太阳辐射量,时隙t的平均太阳辐射强度Ts(t)为

(8)

(8)式中,as、bs、cs为由实测数据拟合所得的太阳辐射强度拟合参数。依据常用的光伏组件发电量模型[13],时隙t的平均光伏供电功率Ppv(t)为

Ppv(t)=Ts(t)·ηpv·Spv

(9)

(9)式中:Spv为光伏板面积;ηpv为光伏板效率。本文规划的光伏容量即为光伏板面积Spv。

1.4 电池储能模型

储能系统一般包含充电、放电以及静置3种状态。单基站电池储能状态模型在单个时隙中,电池只允许处于一种状态,时隙间进行状态切换。当电池处于充电状态时,仅考虑电池由光伏充电,不考虑传统能源给储能电池充电。

1)当处于充电状态时,电池能量状态转移方程式为

Bsoen(t+1)=min{Bsoen(t)+C·ηbatt,Bnc·ηdod,max}

(10)

C=Ppv(t)·Δt-Pbs(t)·Δt,Ppv(t)>Pbs(t)

(11)

(10)—(11)式中:Bsoen(t)为电池储能系统在时隙t起点的能量;C表示单位时隙的电池充入电量;ηbatt为电池充放电效率;Bnc是电池储能容量;ηdod,max为电池充电上限阈值;Ppv(t)是单位时隙光伏供电功率;Pbs(t)是单位时隙基站功率;Δt是单位时隙。

2)当处于放电状态时,电池能量状态转移方程为

Bsoen(t+1)=max{Bsoen(t)-D/ηbatt,Bnc·ηdod,min}

(12)

D=Pbs(t)·Δt-Ppv(t)·Δt-Pgrid(t)·Δt,

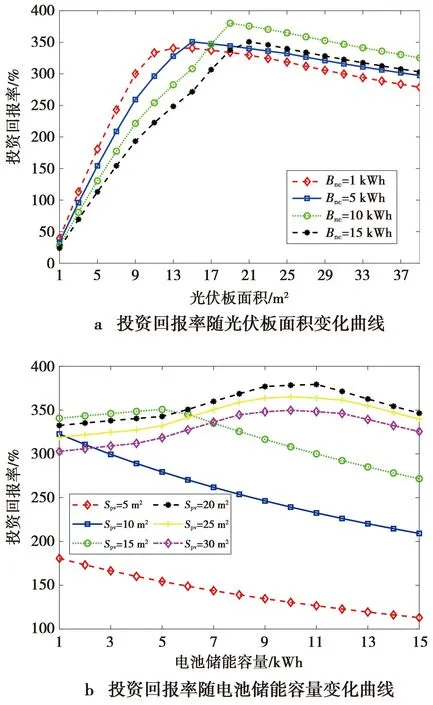
Ppv(t)

(13)

(12)—(13)式中:D表示单位时隙的电池放出电量;ηdod,min为电池放电下限阈值;Pgrid(t)是单位时隙传统能源供电功率。

3)当处于静置状态时,假设静置时间为单位时隙,电池能量状态转移方程为

Bsoen(t+1)=Bsoen(t)

(14)

2 优化建模

2.1 外层优化模型

外层优化模型关注系统经济性指标,通过衡量系统成本与收益,在满足光伏利用率的要求下,对基站布设的光伏板面积和电池储能容量进行规划,使得系统投资回报率最大。

投资回报率(return on investment,ROI)用于衡量商业投资活动盈利能力[14]。投资回报率一般由收益与成本的比值计算而得。本文使用投资回报率衡量基站系统的经济可行性。收益主要包括使用光伏供能后系统节省的电费和节省的碳税[15],成本则主要包括光伏储能系统的建设、运维和更换费用。光伏利用率(utilization of photovoltaic energy,UPE)为蜂窝网络使用的光伏电量与光伏系统总发电量的比值,其描述的是该5G基站系统的光伏消纳能力,光伏利用率越大,则系统弃光越少,光伏就地消纳能力越好。

因此,外层优化问题可描述如下:在给定时间段T内,在已知太阳辐射强度以及基站能耗的前提下,以满足光伏利用率指标为要求,通过求解基站光伏板面积与电池储能容量,使得系统投资回报率最大,即

maxξROI

(15)

s.t.ξUPE>ξUPE,req

(16)

(15)—(16)式中:ξROI为投资回报率;ξUPE为系统光伏利用率;ξUPE,req为系统光伏利用率指标要求。

外层模型将时间尺度T确定为1天,即24小时,其中1小时为一个时隙,则该时间尺度的系统投资回报率ξROI为

(17)

(17)式中:Ggrid,i(t)是单位时隙基站Bi节省的电费;Gcarbon,i(t)是单位时隙基站Bi节省的碳税;Gcost,i是依时间尺度折算后基站Bi建设光伏储能系统的成本。三者计算式为

Ggrid,i(t)=(Pbs,i(t)-Pgrid,i(t))·γgrid·Δt

(18)

Gcarbon,i(t)=(Pbs,i(t)-Pgrid,i(t))·γcarbon·

ηcarbon·Δt

(19)

(20)

(18)—(19)式中:Pbs,i(t)是单时隙基站Bi的功率;Pgrid,i(t)是单时隙基站Bi消耗的传统能源功率;γgrid是传统能源价格;γcarbon是碳税因子[15];ηcarbon是碳排放因子[16];Δt为1小时;Spv,i是基站Bi布设的光伏板面积;Bnc,i是基站Bi布设的电池储能容量;Cpv是单位面积光伏板成本;Cnc是单位容量电池成本;Cother是系统其他部分(如管理单元)的成本;Lpv是光伏板使用寿命;Lnc是电池使用寿命;L是系统使用寿命。

光伏利用率ξUPE表达式为

(21)

(21)式中,Ppv,i(t)是单位时隙基站Bi的光伏发电功率。

2.2 内层优化模型

内层优化模型关注蜂窝网络性能指标,根据基站接入的用户流量进行基站发射功率控制与分配,在满足用户服务速率的要求下,使得蜂窝网络碳排放效率(carbon efficiency,CE)最大。

与网络能量效率、网络频谱效率等传统蜂窝网络度量指标[17-18]类似,蜂窝网络碳排放效率(以下简称为碳效)描述的也是一种资源换取效用的关系,即蜂窝网络通过排放温室气体以换取网络效用。碳效是衡量蜂窝网络碳足迹效率的指标,通常是由蜂窝网络效益与相应的碳足迹作比较获得。碳足迹[19]是对一项活动直接或间接造成的在产品生命周期内二氧化碳总排放量的唯一度量。本文将蜂窝网络的碳排放效率确定为网络下行链路总速率与网络碳排放量的比值,具体碳排放量可通过系统产生碳排放消耗的能源与此能源碳排放因子相乘计算得出。在混合供能蜂窝网络场景下,网络碳效既可以度量蜂窝网络性能,又可以评估光伏供能网络带来的节能减碳作用。网络碳效越大,说明达到同样的性能,网络所排放二氧化碳越少。

因此,内层优化问题可描述如下:在给定时间段T内,在已知太阳辐射强度、满足用户服务质量要求的前提下,通过基站发射功率控制与分配,使得网络碳排放效率最大,即

maxεCE

(22)

s.t.Ri,j>Rreq,∀i∈{1,2,…,Nb},

j∈{1,2,…,Nu,i}

(23)

Pt,i≤Ptmax,∀i∈{1,2,…,Nb}

(24)

(22)—(24)式中:εCE为碳排放效率;Ri,j为蜂窝网络中的用户实际速率;Rreq为蜂窝网络中的用户速率需求;Pt,i为基站总发射功率;Ptmax为基站最大发射功率。

内层模型将时间尺度确定为1小时,即一个时隙。考虑蜂窝网络在使用阶段的碳效,单位时隙的碳排放效率εCE为

(25)

(25)式中:C为网络下行链路总速率;Ecarbon为网络碳排放量。当仅考虑混合供能基站系统在使用周期的碳排放量时,可认为光伏供能不会产生碳排放量[20],所有碳排放量均来源于传统能源。单位时隙的网络碳排放量Ecarbon计算式为

(26)

2.3 模型求解

本文使用双层优化模型求解混合供能蜂窝网络的联合优化问题。外层模型将时间尺度压缩在1天,采用基于模拟退火的粒子群算法求解5G基站系统各个基站的光伏板面积和电池储能容量,要求在保证满足光伏利用率的前提下,使得系统投资回报率最大。内层模型将时间尺度确定在1小时,采用拉格朗日对偶分解方法求解基站发射功率分配策略,要求在满足用户服务速率需求下,使得网络逐小时碳排放效率最优。外层模型将当前光伏板面积和电池储能容量传递给内层模型,内层模型基于当前系统配置求解基站发射功率分配策略,使得单小时的网络碳排放效率最大,在累积优化24小时后,内层模型将单日的网络光伏用量、传统能源用量回馈给外层模型。外层模型依据内层模型输出参量计算单日系统投资回报率,依据粒子群寻优情况调整基站系统配置,并将其传递到内层模型。外层模型中粒子群寻优变量即为基站光伏板面积和电池储能容量,通过退火、自适应变异操作,内外层模型循环迭代求解直至收敛,使得系统投资回报率最大和网络逐小时碳排放效率最优。图2是双层优化模型的求解流程图。

图2 双层优化模型的求解流程图Fig.2 Flowchart of the solution of the two-layer optimization model

2.3.1 基于模拟退火-粒子群的投资回报率优化算法

模拟退火-粒子群算法(simulated annealing-particle swarm optimization algorithm,SA-PSO)[21]结合了粒子群优化算法(particle swarm optimization,PSO)的全局寻优能力和模拟退火算法(simulated annealing,SA)易跳出局部最优解的能力,提高了迭代后期算法的收敛速度与精度。SA-PSO算法体量小,求解程序简单,收敛速度快,适用于不相关的变量求解。由于外层模型中各个基站彼此的光伏板面积和电池储能容量不具备相关性,因而本文使用SA-PSO算法求解外层模型。混合算法在模拟退火各个温度下依次进行粒子群搜索直至迭代结束,最终得到最优解。

在外层模型求解中,SA-PSO算法中粒子群位置即为待求解变量——基站光伏板面积以及电池储能容量。因此,本文将粒子位置拓展成一个2×Nb维矩阵,表示为

(27)

s.t.Spv,min≤Spv,i≤Spv,max

(28)

Bnc,min≤Bnc,i≤Bnc,max

(29)

(27)—(29)式中:x∈2×Nb为粒子位置;i=1,2,…,Nb;Spv,min、Spv,max分别为可配置的最小光伏板面积和最大光伏板面积;Bnc,min、Bnc,max分别为可配置的最小电池储能容量和最大电池储能容量。本文基于SA-PSO的投资回报率优化算法见算法1。

算法1基于SA-PSO的投资回报率优化算法

输入:微粒数M,基站数Nb,微粒速度限制[vmin,vmax],微粒位置限制[xmin,xmax],学习因子c1、c2,预估迭代次数Osum,初始温度To,退温系数λ,最大加权因子wmax,最小加权因子wmin,自适应变异概率p

输出:微粒群最佳位置gbest,最大投资回报率ξROI,max

/*gbest∈2×Nb*/

1:初始化微粒群的位置x、速度v、适应度ffit,迭代次数o=1,并设当前位置为ξROI最大的位置xbest

2:使用(17)—(21)式,计算各微粒的ξROI和ξUPE

3:对于微粒群体,将ξROI最大且满足ξUPE,req的位置存储至gbest,微粒群的ξROI最大值记为ξROI,max

4:whileffit≠0 do

5: 计算各微粒xbest的适应度为

ffit(ξROI)←(ffit,1,…,ffit,M)

7: 计算微粒速度更新权重w为

/*权重w采用线性递减权值策略[21]*/

8: 更新各微粒的速度

9: 限制各微粒的速度和位置

10: 以概率p随机改变第m个粒子的位置

xm←xmin+r3·(xmax-xmin)

11: 使用(17)—(21)式,计算各微粒的ξROI和ξUPE

12: 更新gbest、ξROI,max

13: 执行退温操作To←λTo

14: 记录迭代次数o←o+1

15: end while

/*r1、r2和r3是[0,1]之间的随机数*/

2.3.2 基于拉格朗日对偶分解的碳效优化算法

内层模型的优化问题转换如下。

存在最优碳效值的充要条件为

(30)

(31)

s.tRi,j>Rreq,∀i∈{1,2,…,Nb},

j∈{1,2,…,Nu,i}

(32)

Pt,i≤Ptmax,∀i∈{1,2,…,Nb}

(33)

(31)式中,基站消耗的传统能源功率Pgrid,i为

Pgrid,i(Pt,i)=[Pbs,i-Ppv,i]+=

(34)

上述问题的拉格朗日对偶问题可表示为

(35)

(35)式中,χi、γi,j为拉格朗日乘子。

将(4)、(5)、(7)、(34)式代入(35)式中,问题转化为

(36)

s.t.χi≥0,∀i∈{1,2,…,Nb}

(37)

γi,j≥0,∀i∈{1,2,…,Nb},j∈{1,2,…,Nu,i}

(38)

根据KKT条件[22-23]求解上述问题,得到功率分配策略为

(39)

使用梯度下降法[22]对拉格朗日乘子进行求解,得

(40)

(41)

通过迭代计算直到拉格朗日乘子收敛,得到最优功率分配策略。

3 仿真分析

3.1 实验环境与仿真参数

为了验证上述模型求解方法的有效性,本文使用表1—表4的参数进行仿真。其中,表1的光伏供能系统参数和表2的电池储能系统参数参考文献[24];表3的蜂窝网络基站参数参考文献[2,12],传统能源价格参考国家工商业电价,碳税因子参数参考文献[25],碳排放因子参数参考文献[2];表4中模型求解算法参数通过多次模型仿真收敛性测试获得。本文实验环境为Intel(R) Core(TM) i5-10400F CPU @ 2.90 GHz,8 GB内存,64位操作系统,实验系统为windows 10,仿真平台是MATLAB R2022a。

表1 光伏供能系统仿真参数

表2 电池储能系统仿真参数

表3 蜂窝网络仿真参数

表4 模型求解算法参数

使用武汉、北京、深圳和拉萨的 2021 年 1 月 1 日至 2021 年 12 月 31 日每日逐小时太阳辐射数据集(来源于欧洲中期天气预报中心)进行基站单日太阳辐射数据拟合,得到典型日太阳辐射曲线,如图3所示。使用正态分布函数拟合不同地区日太阳辐射强度,其R2拟合优度均可达99.0%以上。但当使用不同地方的太阳辐射数据时,其拟合的正态分布函数曲线数值不同。由于地区日照条件不同、经纬度存在差异,因此,不同地区的日太阳辐射强度最大值及其出现时间点均存在差异。拉萨位于我国西部,最大日照点约在14时;武汉、北京和深圳位于我国东部,最大日照点约在12时。基站接入用户仿真曲线[12]如图4所示。

图3 典型日太阳辐射曲线Fig.3 Curve of typical daily solar radiation

图4 基站接入用户曲线Fig.4 Curve of the base station access users

3.2 仿真结果分析

3.2.1 投资回报率优化算法

基于模拟退火-粒子群的投资回报率优化算法通过调整光伏板面积和电池储能容量参数,使得系统投资回报率最大。图5是模拟退火-粒子群算法、粒子群算法和模拟退火算法的迭代寻优对比分析结果。由图5可知,SA-PSO算法和PSO算法在2-3次迭代后即可寻找到使得投资回报率最大的光伏板面积和电池储能配置;SA算法的迭代曲线呈阶梯式渐进趋势,在30次迭代后才能寻找到投资回报率最优点;PSO算法利用多粒子并行搜索最优点,全局寻优能力较好;SA算法串行搜索,速度慢于PSO算法,但其跳出局部最优的能力较好;SA-PSO算法兼两者之长,寻优速度优于PSO算法和SA算法。仿真结果与算法特点吻合。图6是不同粒子数的SA-PSO算法对比分析图。由图6可见,当只有2个粒子寻优时,在50次迭代后仍无法找到投资回报率最优点。粒子越多,算法寻优速度越快。当粒子数大于20时,经过2-3次迭代后即可寻到全局最优投资回报率。

图5 算法对比图Fig.5 Graph of algorithm comparison

图6 不同粒子数的SA-PSO算法对比图Fig.6 Comparison chart of SA-PSO algorithm with different particle numbers

算法结果如表5所示。以武汉为例,使用3.1中仿真参数所得最优投资回报率为381.3%,对应光伏板面积为18.4 m2,电池储能容量为9.3 kWh,此时光伏利用率为96.5%。当使用不同地方的太阳辐射数据时,模型算法的输出结果不同。由图3可知,在4个地区中,拉萨日太阳辐射峰值最大;由表5可知,算法输出的拉萨对应光伏板面积最小,成本最低,投资回报率最大。

表5 各地区基站投资回报率优化结果

进一步分析系统投资回报率随系统配置的变化趋势(以武汉为例)。图7是系统投资回报率分别随基站光伏板面积和电池储能容量的变化曲线。

图7 投资回报率曲线Fig.7 Curve of return on investment

由图7a可见,随着基站光伏板面积增多,基站投资回报率呈先增大后缓慢减小趋势,且随着电池储能容量的增大,投资回报率最大值对应的光伏板面积随之增大。由图7b可见,当光伏板面积较小时,随着电池储能容量的增大,基站投资回报率呈减小趋势;当光伏板面积较大时,随着电池储能容量的增大,投资回报率呈先增大后减小趋势。

3.2.2 碳效优化算法

碳效优化算法效果分析中,以采用碳效优化算法与不采用碳效优化算法进行对比分析(以武汉为例)。其中,不采用碳效优化算法的对比方案为使用注水算法[26]进行功率分配,基站始终保持最大发射功率工作。图8为单日累积碳排放量对比图。图8中,CEOA为碳效优化算法(carbon efficiency optimization algorithm,CEOA)。在一天时间内,未使用CEOA的基站累积碳排放量为26.29 kgCO2,使用CEOA的基站单日累积碳排放量为17.93 kgCO2。使用CEOA进行发射功率控制,降低了31.8%的碳排放量。

图8 有无碳效优化算法的基站日累积碳排放量对比曲线Fig.8 Comparison curve of daily cumulative carbon emissions of base stations with or without carbon efficiency optimization algorithm

以武汉为例进一步分析单基站碳效随系统配置的变化趋势。图9展示了基站碳效分别随基站光伏板面积和电池储能容量的变化曲线。由图9a可见,随着基站光伏板面积增加,基站碳效先增大后趋于不变。在一定范围内,光伏板面积越大,基站使用的光伏能量越多,碳排放量越小,碳效越大;超出此范围,碳效趋于稳定。这是因为受基站能耗限制,可减少的碳排放量是有限的。电池储能容量越大,碳效曲线转折点对应的光伏板面积就越大,碳效最大值也越大。由图9b可见,当光伏板面积较小时,基站碳效不受电池储能容量影响,这是因为光伏能量全部用于基站,无多余能量存储到电池;当光伏板面积较大时,随着电池储能容量增大,碳效先增大后趋于不变。

图9 碳效曲线Fig.9 Curve of carbon efficiency

以武汉为例分析单基站碳效随太阳辐射强度最大值的变化趋势。取投资回报率最优的基站配置——光伏板面积为18.4 m2、电池储能容量为9.3 kWh,可得基站碳效随日太阳辐射强度最大值的变化曲线,如图10所示。由图10可知,随着地区太阳辐射量的增多,基站碳效先增大后趋于不变。在一定范围内,太阳辐射量越多,基站使用的光伏能量越多,碳排放量越小,碳效越大;超出此范围,碳效趋于稳定,此变化趋势与基站碳效随基站光伏板面积的变化趋势一致。

图10 碳效随日太阳辐射强度最大值变化曲线Fig.10 Curve of carbon efficiency changing with the maximum value of daily solar radiation

综上所述,本文通过基于光伏容量与储能容量可变的系统经济性分析,计算得到在仿真条件下满足光伏利用率和用户服务速率的5G基站系统规划结果——基站光伏板面积和电池储能容量配置,并得到了系统的最优投资回报率和最优碳效。

4 结束语

本文针对混合供能蜂窝网络的场景,提出双层优化模型以求解5G基站系统的投资回报率和碳效优化问题。本文通过对光伏储能系统配置的5G基站系统经济性分析,分别得出了系统投资回报率、碳效与系统的光伏板面积和电池储能容量的关系。仿真结果表明,求解所提出的双层模型不仅可给出满足用户服务质量且碳排放效率最优的基站功率分配策略,还能给出满足光伏利用率要求且经济性最优的基站光伏板面积和电池储能容量配置。使用本文算法可使得全系统投资回报率达到380.3%,光伏利用率达到96.5%;其内层的碳效优化算法相较于注水算法碳排放量降低了31.8%。本文使用的模型算法未考虑不同基站由于周边环境不同而导致的光伏布设面积限制差异,下一步工作将完善模型算法,进一步考虑基站的光伏板面积配置限制差异,使得模型算法计算结果更具有实用价值。