一种融合时差频差和测向的运动目标跟踪方法*

徐海源,苏成晓,汪华兴

(北京市遥感信息研究所,北京 100011)

0 引 言

星载无源定位系统通过侦收地球表面或具有一定高程的雷达、通信等辐射源的辐射信号,采用单星或多星定位体制获取辐射源的位置信息。其中,由星座构成的无源定位系统具有覆盖面积大、定位精度高的优点,通过建立时差、频差等参数测量方程,结合地球表面约束方程可以实现已知高程辐射源的高精度定位[1-3]。对于运动辐射源,无源定位系统需要估计其每一时刻的位置,并进一步得到速度信息,即实现目标的跟踪。对于未知高程的空中运动目标的无源定位跟踪,假设高程的定位方法将带来较大的跟踪误差。

目前,已有相关文献研究了基于星座体制无源定位系统的空中运动目标的定位跟踪问题。文献[4]在三星时差定位系统中增加一维干涉仪测方位角信息实现未知高程目标的定位,并通过无迹卡尔曼滤波(Unscented Kalman Filter,UKF)提高定位精度,但垂直于主星飞行方向存在不可观测区域。文献[5]提出了假定高程下的三星时差、频差运动辐射源定位和测速求解方法,但在高程估计误差较大时将导致定位误差和测速误差增大。文献[6]研究了双星时差、频差融合二维角度信息的运动目标跟踪方法,但仍假设目标高程为已知量参与跟踪滤波。文献[7]采用主星高精度测向和双星时差联合实现空中目标高精度定位,但需要较高的测向精度,传统的干涉仪测向系统难以满足要求。文献[8]提出了一种三星时差、频差融合一维干涉仪测向信息的改进迭代卡尔曼滤波动目标跟踪方法,能够提高未知高程目标的位置、速度估计性能,但更适合三星同轨编队的应用场景,并且也存在不可观测区域。

针对由3颗卫星构成的无源定位系统,采用异轨三角形构型能够获得更高的时差定位精度分布[9];若采用同轨编队构型,将导致星下点附近存在不可观测区域,对地球表面已知高程的固定或慢速目标的定位性能带来较大损失。因此,在异轨编队三星时差、频差定位系统基础上,本文提出在其中一颗卫星上增加二维干涉仪测向信息,然后采用迭代扩展卡尔曼滤波(Iterative Extended Kalman Filter,IEKF)方法实现未知高程运动目标的跟踪滤波。

1 三星时差、频差和二维测向融合跟踪模型

本文考虑的无源定位系统由异轨三星构成,假设一颗卫星上安装二维干涉仪,并且与另外两颗星之间可测得辐射源信号到达时间差(Time Difference of Arrival,TDOA)和多普勒频差(Frequency Difference of Arrival,FDOA)。在目标定位跟踪中,一般采用WGS-84坐标系描述目标的状态,因此本文在WGS-84坐标系下建立未知高程运动目标跟踪的状态方程和观测方程。

1.1 状态方程

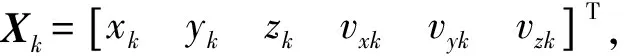
Xk=AXk-1+wk-1

(1)

(2)

式(1)中:A为状态转移矩阵;wk-1为过程噪声,其均值为0;协方差矩阵为Qk-1;Δt为观测时间间隔。

对于CV模型,状态噪声协方差Qk-1表示为[10]

(3)

1.2 观测方程

在干涉仪测向系统中,原始观测量为相位差φ,通过式(4)可以得到角度测量值β:

(4)

式中:n=d/λ,d为干涉仪基线长度,λ为信号波长。

由式(4)可以看出,角度与相位差呈现非线性关系,因此角度测量误差随着角度变化而发生变化。而干涉仪相位差测量误差在地面可以准确测量,且不随目标所在的方向而变化,因此本文将干涉仪相位差作为观测量。假设星体坐标系下辐射源的位置为(xb,yb,zb),则方位、俯仰向的相位差φA和φB可表示为

(5)

(6)

式中:mij为坐标旋转矩阵M中的元素。于是,式(5)可表示为

(7)

Zk=h(Xk)+vk=

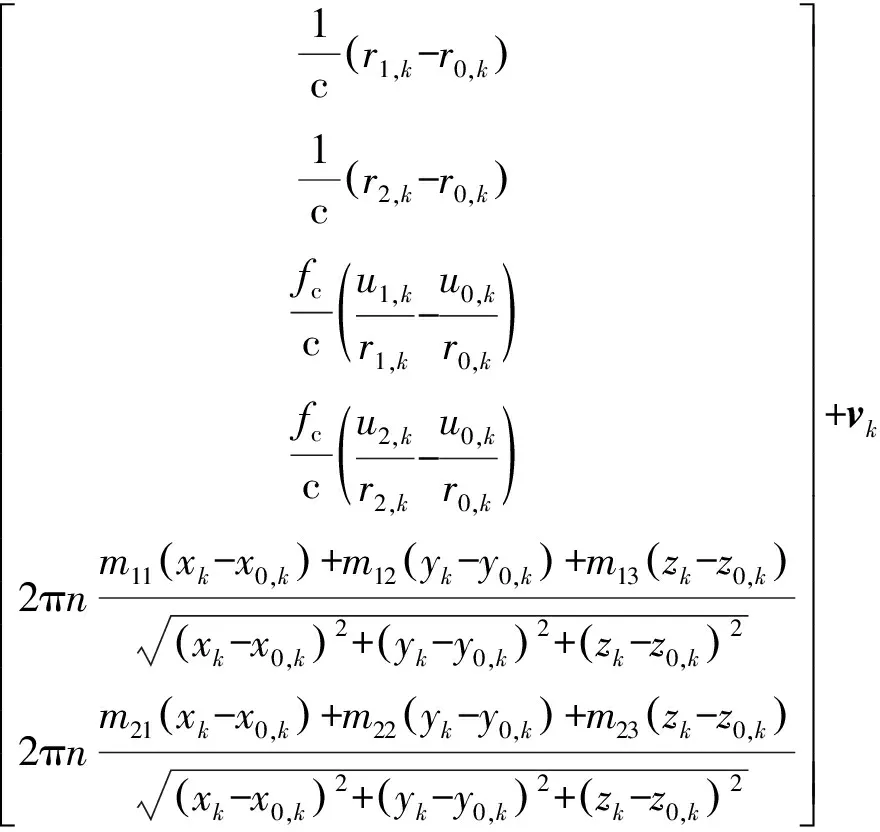
(8)

ui,k=(xi,k-xk)(vxi,k-vx,k)+(yi,k-yk)(vyi,k-vy,k)+

(zi,k-zk)(vzi,k-vz,k)

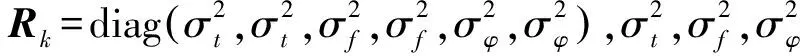
2 IEKF跟踪算法

由于观测方程为非线性方程,需要采用非线性滤波方法提高对运动目标位置和速度的估计精度。扩展卡尔曼滤波(Extended Kalman Filter,EKF)算法通过对非线性方程做线性化截断处理,并只保留一阶泰勒级数的展开项,以达到线性化的目的,是一种次优非线性滤波算法。迭代扩展卡尔曼滤波算法通过多次计算量测更新环节,即反复地去线性化量测方程,并根据量测值修正估计值,以逐渐减小估计误差,从而提升滤波精度[11]。本节采用IEKF算法基于上节建立的状态方程和观测方程进行空中运动目标的跟踪滤波。

2.1 滤波初始化

1)目标状态初始值

2)初始预测协方差矩阵

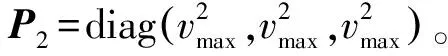
2.2 IEKF跟踪算法步骤

由于观测量中相位差的直接测量值会出现模糊,在实际应用中需要首先去除相位差模糊。采用IEKF跟踪算法的步骤如下:

1)计算三星时差定位结果

2)得到无模糊相位差

3)目标状态和协方差矩阵预测

Xk/k-1=AXk-1/k-1

Pk/k-1=APk-1/k-1AT+Qk

4)设置迭代初值

X0=Xk/k-1

P0=Pk/k-1

5)开始迭代

②计算卡尔曼增益矩阵

Kj=P0(Hj)T[R+HjP0(Hj)T]-1

③更新目标状态

Xj+1=X0+Kj[Zk-h(Xj)-Hj(X0-Xj)]

④更新协方差矩阵

Pj+1=P0-KjHjP0

当达到设定迭代次数或条件时终止迭代,本文采用‖Xj+1-Xj‖≤ε作为迭代终止条件,ε为设定的门限值。

6)更新目标状态和协方差矩阵

Xk/k=XN

Pk/k=PN

3 仿真分析

为验证提出的三星时差、频差和二维测向融合的空中运动目标跟踪方法的有效性,建立典型场景进行了仿真分析。3颗卫星采用双星同轨、一星异轨的构型,卫星轨道高度均为700 km,星间距80 km,其中异轨卫星上安装二维正交干涉仪,基线长度3 m;目标高程为10 km,作速度为300 m/s的匀速直线运动;目标辐射源频率为3 GHz。时差测量误差为20 ns,频差测量误差为1 Hz,相位差测量误差为15°。观测时间间隔为1 s,图1给出了跟踪时长为150 s后的定位误差(含高程误差)几何精度因子(Geometric Dilution of Precision,GDOP)分布仿真结果,单位为km;其中,目标高度误差GDOP分布仿真结果如图2所示,单位为km。从图1中可以看出,对存在高程的空中运动目标,在三星异轨构型下,采用本文所提的方法跟踪滤波后能在较大的范围内达到较高的定位精度,这与同轨三星的目标跟踪方法在星下点附近存在不可观测区域是不同的[4,8]。由于三星时差频差定位系统对地球表面目标的定位误差分布与星座构型密切相关,采用三星异轨形成近似三角形构型能够在更大的范围内实现较高的目标定位精度。因此,本文提出的在异轨三星中的一颗星上增加正交干涉仪,通过时差、频差融合相位差的IEKF跟踪算法,可以提升三星时差频差定位系统对空中运动目标的定位跟踪能力,同时也保证了其对地球表面大范围固定目标和慢速目标的定位能力。从图2中可以看出,对目标高度的估计误差在较大范围内可以达到百米量级,表明所提方法能够有效估计未知运动目标的高度信息。

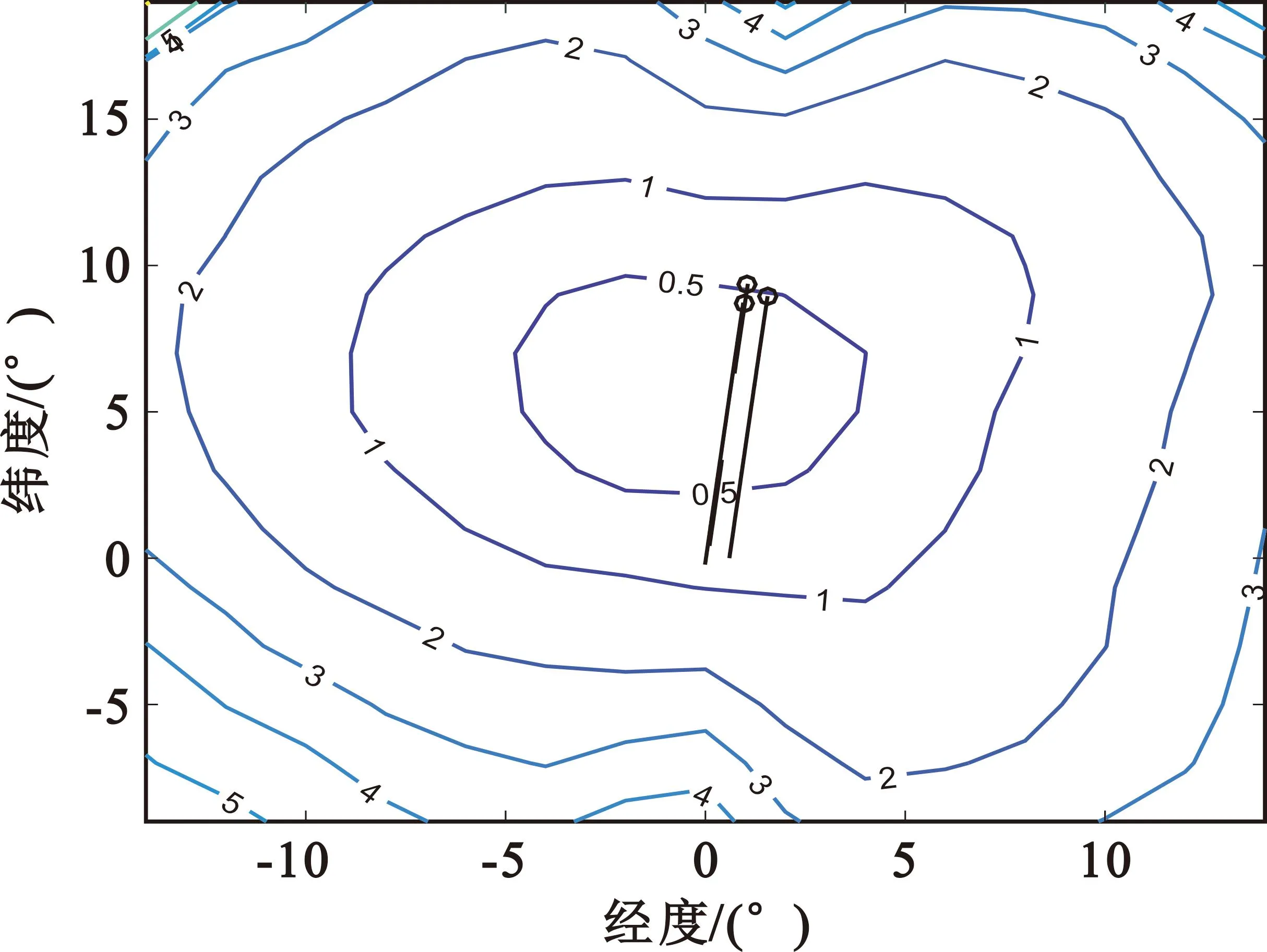
图1 定位误差GDOP分布

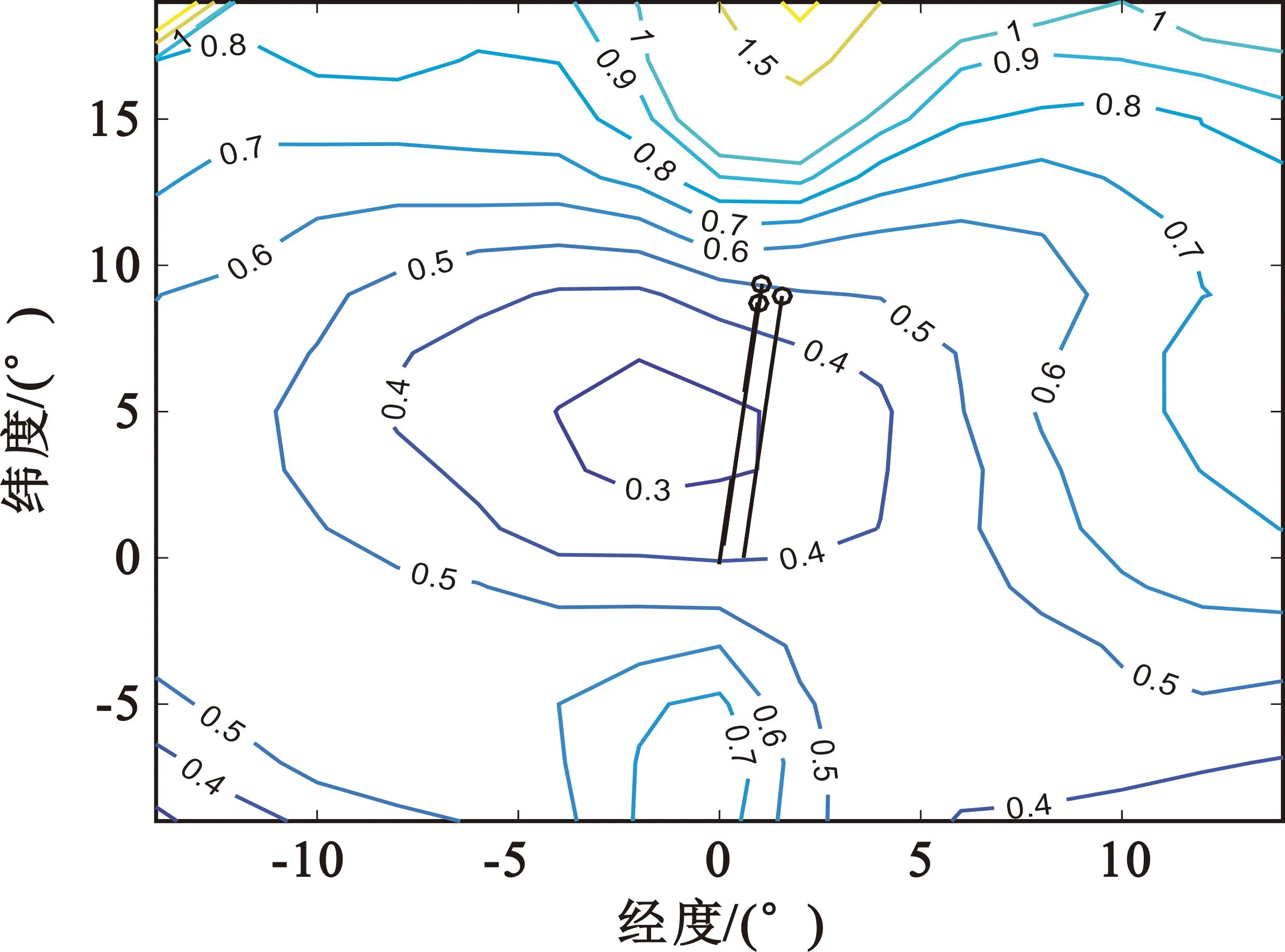
图2 高度误差GDOP分布

在三星覆盖区域内选取一个目标位置,按照上述目标运动参数和观测量误差对采用不同观测量的IEKF跟踪滤波方法的性能进行仿真比较。针对三星时差频差+一维测向、三星时差+一维测向和本文三星时差频差+二维测向等3种方法,分别进行了100次蒙特卡罗仿真,对目标位置、高度、航速和航向估计误差进行了比较,结果如图3～6所示。

图3 位置估计误差

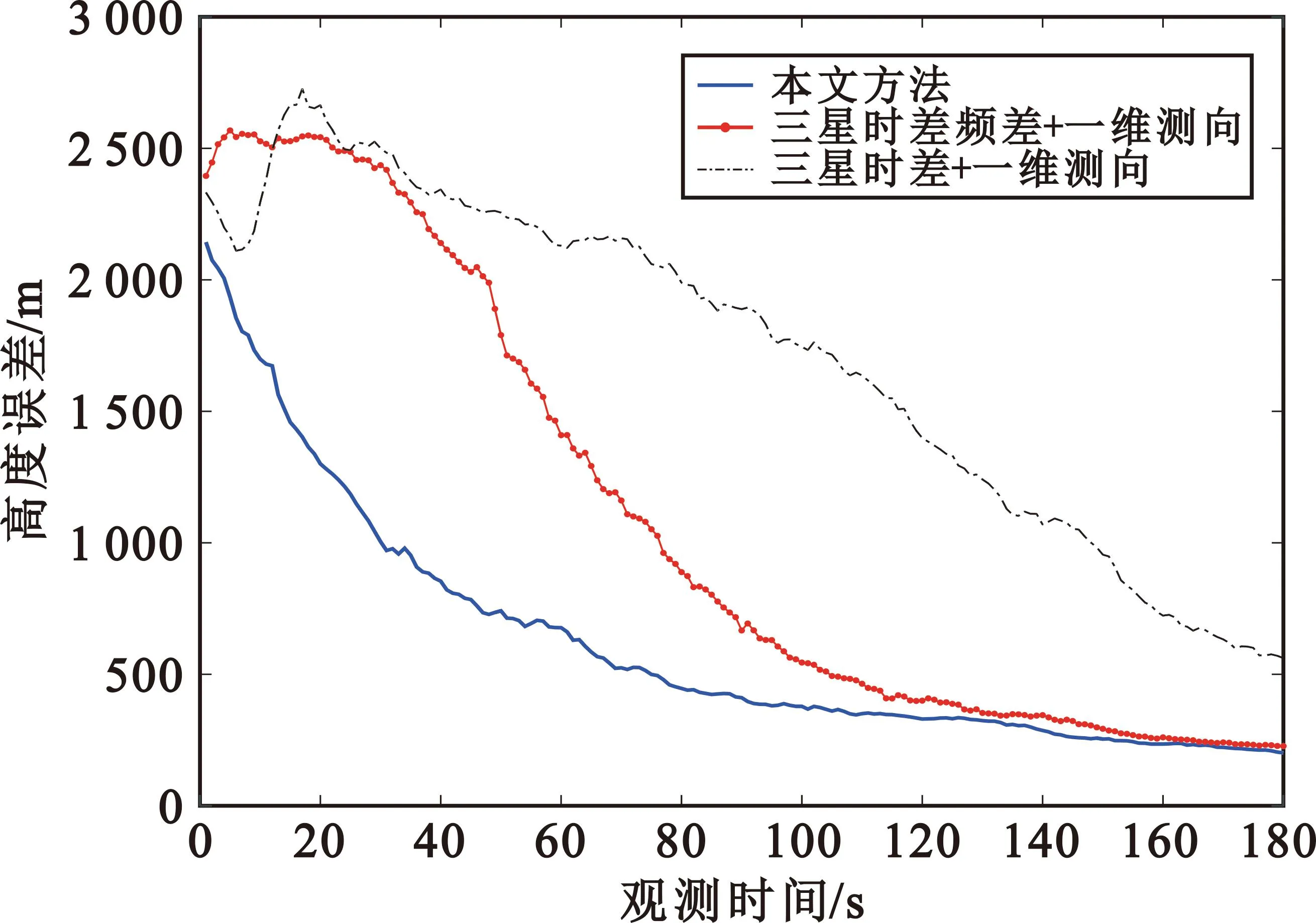
图4 高度估计误差

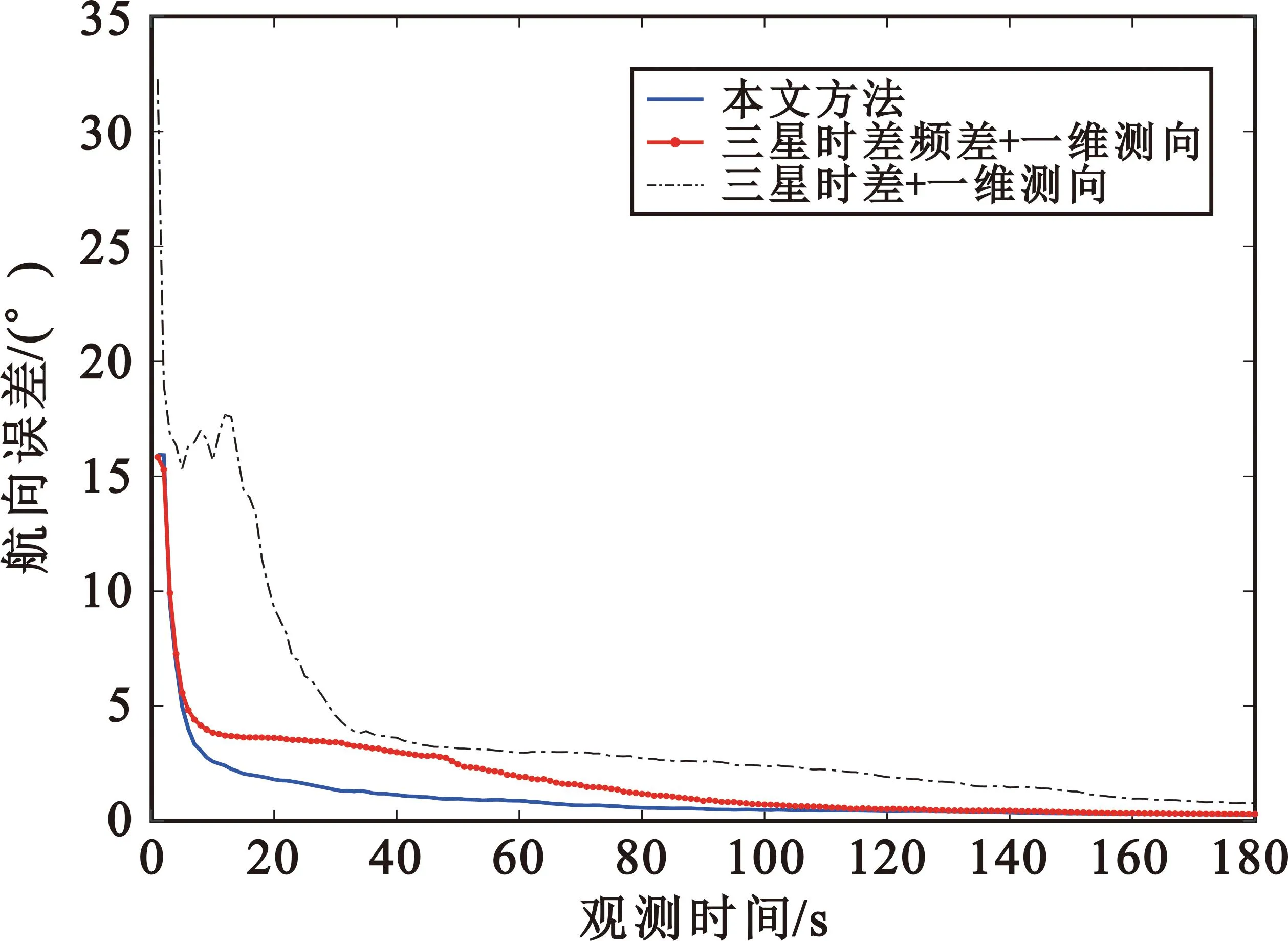
图6 航向估计误差

从图中可以看出,3种方法均可以实现未知高程目标的跟踪定位,但三星时差+一维测向的跟踪方法估计误差最大,收敛速度较慢;三星时差频差+一维测向的跟踪方法由于引入频差测量信息,在位置、速度估计精度方面有大幅提高;而本文的三星时差频差+二维测向跟踪方法通过增加一维测向信息,位置(含高度信息)、速度估计精度均进一步提高,且收敛速度更快。

4 结 论

本文针对星载无源定位系统对未知高程运动目标的定位跟踪问题,提出了一种基于异轨三星时差频差和二维测向融合的跟踪滤波方法。在WGS-84坐标系下建立了由二维时差、二维频差和二维相位差构成的观测方程,并采用IEKF方法进行跟踪滤波。仿真结果表明,本文所提的目标跟踪方法在目标高程未知的情况下,能够实现运动目标位置、高度、航速和航向的高精度估计,相对已有方法在收敛速度和估计精度上有明显提高,并且可以获得更大范围的高精度定位跟踪结果。