地铁车站嵌套式隔振柱的动力特性分析

王智弘，金 浩，夏瑞萌，顾兴宇

(1.东南大学交通学院,南京 211189; 2.北京城建设计发展集团股份有限公司,北京 100037)

引言

随着我国城市轨道交通的快速发展,各大城市建立了较为完备的地下交通体系,城市交通拥堵问题得到缓解,然而地铁网逐步密集带来的环境振动问题也愈发严重。由车辆-轨道系统运行产生的振动经由轨道结构、隧道结构或车站结构,引起沿线建筑结构振动。这种振动虽振幅小,但持续时间长,给居民日常生活带来了一定影响。目前,常用的减振措施主要针对振源、传播路径以及敏感目标进行研发[1]。其中,以地铁列车与轨道系统为代表的研究已经相对成熟,并成功运用到工程实践中。

近年来,从建筑物本身出发进行的减隔振研究发展迅速,吸引了广大学者的注意。常用的隔振结构通常设置在建筑物主体结构与基础之间,即为基础隔振[2]。基础隔振如叠层橡胶减振系统[3]、复位弹簧和平面滑板并联机构[4]、摩擦摆支座体系(FPS)[5]等隔振结构已经用于工程实践中。叠层橡胶减振系统已相对成熟,能满足自振周期较短的房屋隔振性能要求。其不足之处是对竖向振动一般没有减振效果,对于长周期振动存在危险性[6]。

针对这种现象,一种常见的思路是减小支座竖向刚度来达到减振的目的。例如,厚叠层橡胶支座通过增加橡胶层的厚度以达到降低竖向刚度的目的,ZHOU等[7]研究发现,厚叠层橡胶和三维非线性隔振支座会具有更好的竖向振动隔离能力;PENG等[8]将厚肉型叠层橡胶支座和油阻尼器的隔振系统应用于日本某两层声学实验室,该系统的竖向频率为5 Hz,同时能隔离地震和地铁振动响应;邹立华等[9]在普通橡胶支座的基础上,增大橡胶厚度,提出一种预应力厚叠层橡胶支座,研究表明,该支座不仅有普通橡胶支座的功能,还有良好的水平限位功能。另一种思路是将竖向隔振装置与水平隔振装置组合。葛楠等[10]提出一种新型的FPS摩擦摆与碟型弹簧组合隔震系统,通过降低竖向刚度实现三维隔振;魏陆顺等[11]提出一种新型三维隔振支座,竖向隔振支座和水平隔振支座具有较小刚度,研究表明,支座对于振动的高频信号具有显著衰减效果;吴从晓等[12]研发了一种竖向隔振支座,用于降低地铁竖向振动,并用SAP2000进行模拟分析;李雄彦等[13]提出一种适用于大跨空间结构的碟簧-叠层橡胶支座,研究表明,三维复合隔振支座在水平及竖向均有较好的滞回性能,竖向刚度的降低使支座的水平等效刚度、等效阻尼比增加;曹迎日等[14]提出的碟簧-单摩擦摆三维隔震(振)装置(3DFPS)由碟簧竖向隔振单元和单摩擦摆水平隔震单元组成,可以实现环境激励工况下建筑结构的竖向隔振与地震工况下的水平隔震;王维等[15]设计一种新型三维多功能隔振支座,由铅芯橡胶隔振支座、碟形弹簧组成,通过研究,该支座延长了结构水平和竖直方向的自振周期,对结构的振型影响较大。

基于上述两种思路,并根据振动波传播的路径特点,对叠层橡胶系统没有竖向减振作用这一缺陷进行改进。根据异形U状嵌套结构这一设计要点,以橡胶减振柱为主要嵌套形式,提出了一种新的隔振柱。通过模态分析、频域下加速度传递率分析验证该结构对于减少竖向振动的有效性。

1 嵌套式竖向隔振柱

以雄安至北京大兴国际机场快线(R1线)金融岛站某站台柱为研究对象,该站台柱尺寸为1.4 m×1.1 m×9.45 m。站台柱底部以两个异形U状钢结构进行嵌套,产生3个嵌套单元。嵌套单元水平面上设置橡胶减振柱。初始模型中的异形U状钢结构底部平面长宽比为1,中部支撑宽度为0.4 m,橡胶减振柱的截面半径尺寸为0.55 m。整体模型示意如图1所示。基于异形U状嵌套钢结构这一设计要点,在建模过程中忽略不均匀和内部空隙的影响,建立的隔振柱模型如图1所示。

各部件均选用线弹性材料,并在模态分析前根据选用材料确定杨氏模量、密度及泊松比,如表1所示。

表1 模型材料参数Tab.1 Model material parameters

2 分析工况

设置对照组模型,如图2所示,下部的普通橡胶支座为叠层橡胶减振系统的简化模型。探究在站台柱下设置异形U状嵌套钢结构是否有竖向隔振效果的提升。

图2 普通隔振柱模型Fig.2 General vibration isolation column model

分析三类工况变量,分别为异形U状嵌套钢结构底部长宽比、纵向支撑宽度以及橡胶减振柱截面尺寸。异形U状嵌套钢结构底部长宽比及纵向支撑宽度具体释义如图3所示。三类工况变量均在初始嵌套隔振柱模型的基础上进行分析。分别对初始隔振柱模型橡胶减振体截面半径的85%以及75%进行研究;对初始隔振柱模型异形U状嵌套钢结构中部支撑宽度的1.1倍及1.2倍进行研究;在初始隔振柱模型异形U状嵌套钢结构底部长宽比为1的基础上,开展长宽比分别为1.1及1.2的隔振性能研究,上述工况变量如表2所示。

表2 工况变量Tab.2 Working condition variables

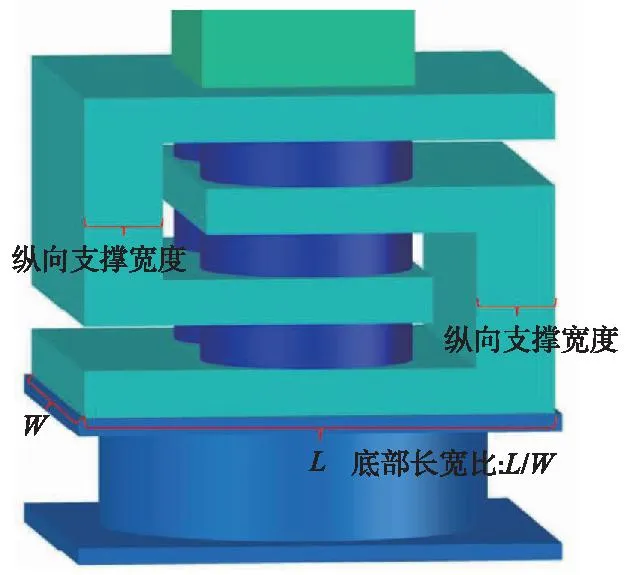
图3 工况变量释义Fig.3 Interpretation of working condition variables

3 嵌套式隔振柱模态分析

3.1 嵌套式隔振柱基频分析

由于固有频率是结构的固有属性,只与材料的弹性模量、泊松比以及边界条件有关,外部荷载对其影响很小[16]。为更真实地模拟在实际应用过程中的动态性能,并预测隔振柱的实际振动响应,将站台柱顶面与基础支座底面固定,求解隔振柱的振动频率及模态振型。

在约束模态分析中,低阶模态通常表征结构的整体特性,高阶模态反映结构的局部特性[17]。在地铁车站实际运营中,相对较低的固有频率值对站台柱共振来讲是危险的,所以也是模态分析所关注的重点。其中,一阶频率也称为基频,是系统的最低振荡频率。基频数值越小,受到外界激励时,更容易实现减隔振的功能。

取嵌套式隔振柱模型各工况前10阶自由模态进行计算,并按一阶模态频率即基频进行比较,如表3所示。

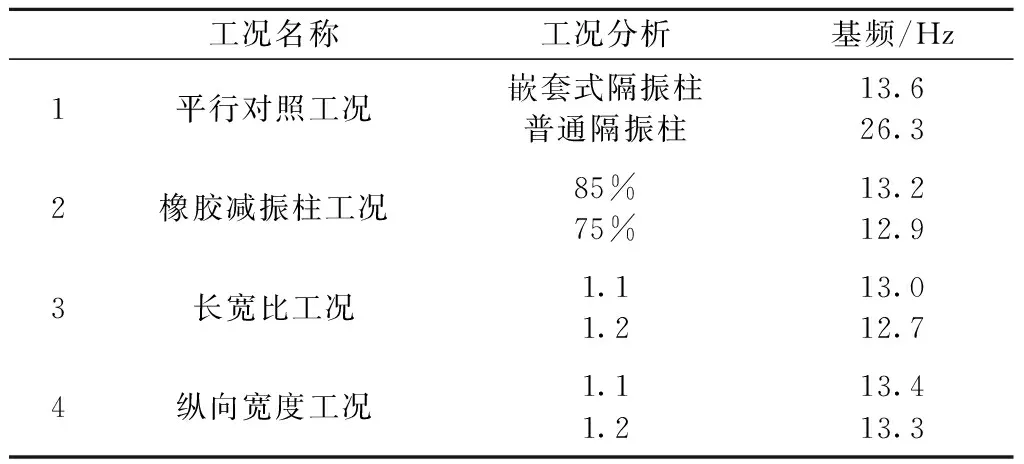
表3 各工况基频对比Tab.3 Comparison of fundamental frequency for each working condition

由工况1分析可知,普通隔振柱的基频为26.3 Hz,在站台柱下增设异形U状嵌套钢结构后,基频为13.6 Hz,降低了12.7 Hz,从而说明设置异形U状嵌套钢结构后有明显的竖向隔振效果。

由工况2分析可知,降低橡胶减振体截面半径尺寸到初始隔振柱模型的85%与75%,分别为0.47,0.41 m;隔振柱基频由13.6 Hz分别降低到13.2,12.9 Hz。因此,从隔振角度出发,适度降低橡胶减振柱体的截面尺寸能够使隔振柱结构的竖向隔振性能增加。

由工况3分析可知,在初始隔振柱模型的基础上,增加异形U状嵌套钢结构底部长宽比至1.1倍、1.2倍,隔振柱基频由13.6 Hz分别降低到13.0,12.7 Hz,从而说明,随着长宽比增加,隔振柱更容易实现竖向隔振的目的。

由工况4分析可知,增加异形U状嵌套钢结构中部支撑宽度至初始隔振柱模型的1.1倍、1.2倍,隔振柱基频由13.6 Hz分别降低到13.4,13.3 Hz。因此,从隔振角度出发,增加异形U状嵌套钢结构中部支撑宽度可使得隔振柱更容易实现竖向隔振的目的。

3.2 嵌套式隔振柱典型模态分析

以初始嵌套隔振柱模型为例,对振型图进行分析。

简化模型的1阶模态固有频率为13.6 Hz,对应的模态振型如图4(a)所示,振型特征为隔振柱侧向弯曲。从振型图可以看出,当隔振柱发生该阶模态振动时,隔振柱底部的普通橡胶支座扭转位移量较大,有侧翻倾向,同时带动上部隔振柱偏移,上部隔振柱特别是异形U状嵌套钢结构保持原有结构相对稳定。因此,在激励频率接近该基频频率时,结构对应的薄弱环节发生于隔振柱下部的叠层橡胶支座区域。

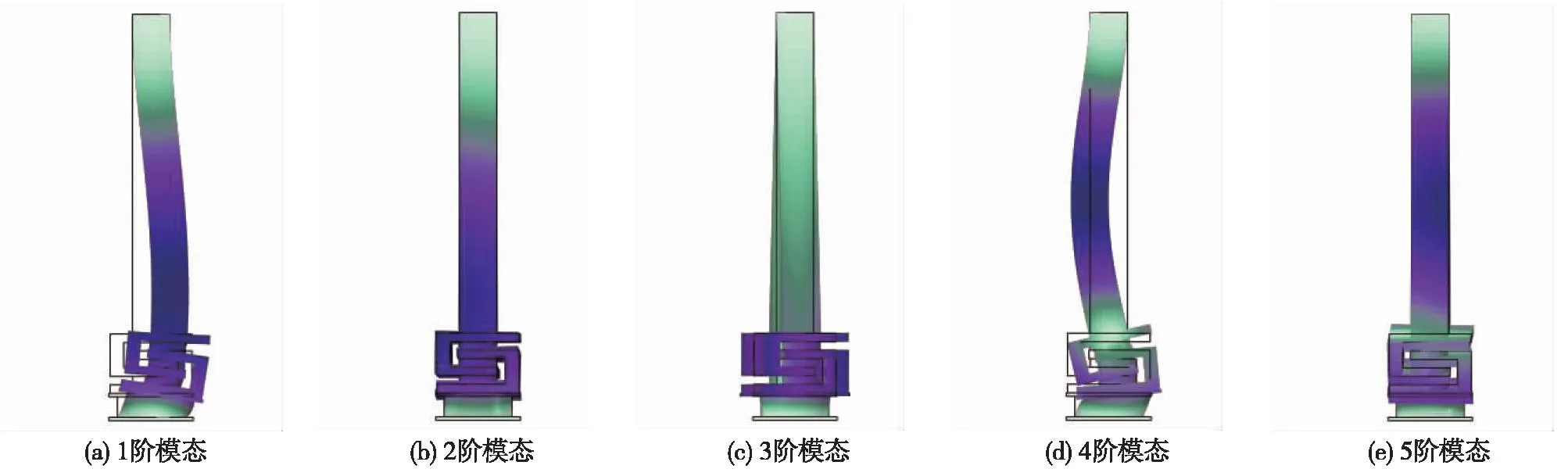
图4 嵌套式隔振柱简化模型前5阶模态Fig.4 Simplified model of nested vibration isolation column with first 5 order modes

简化模型的2阶模态固有频率为15.0 Hz,对应的模态振型如图4(b)所示,振型特征为结构基本保持相对稳定。从振型图可以看出,当隔振柱发生该阶模态振动时,隔振柱整体偏移较小,维持稳定状态。

简化模型的3阶模态固有频率为17.9 Hz,对应的模态振型如图4(c)所示,振型特征隔振柱保持相对稳定。从振型图可以看出,当隔振柱发生该阶模态振动时,异形U状嵌套钢结构发生水平面内的扭转,产生变化的扭转剪切力,通过自身的扭转变形实现竖向隔振。因此,在激励频率接近该固有频率时,隔振柱能实现竖向的隔振。

简化模型的4阶模态固有频率为29.1 Hz,对应的模态振型如图4(d)所示,振型特征为隔振柱整体结构失稳。从振型图可以看出,当隔振柱发生该阶模态振动时,隔振柱柱体中部区域发生明显的弯曲变形,异形U状嵌套钢结构扭转失稳,底部支座产生侧向偏移,结构整体变形较大。因此,隔振柱在该阶模态振动下未能实现隔振。

简化模型的5阶模态固有频率为33.9 Hz,对应的模态振型如图4(e)所示,振型特征为结构基本保持相对稳定。从振型图可以看出,当隔振柱发生该阶模态振动时,只有异形U状嵌套钢结构出现了纵向伸缩变形,说明在竖向振动的扰动下,嵌套式隔振柱实现了良好的隔振效果。

简化模型的6阶模态固有频率为49.3 Hz,对应的模态振型如图5(a)所示,振型特征为异形U状嵌套钢结构底部失稳。从振型图可以看出,当隔振柱发生该阶模态振动时,异形U状嵌套钢结构发生较大逆时针扭转,底部支座产生侧向偏移,而上部隔振柱结构保持相对稳定,偏移量较小。因此,在该阶模态振动下,异形U状嵌套钢结构实现了相对较好的隔振,利用自身变形稳定了上部柱体结构。

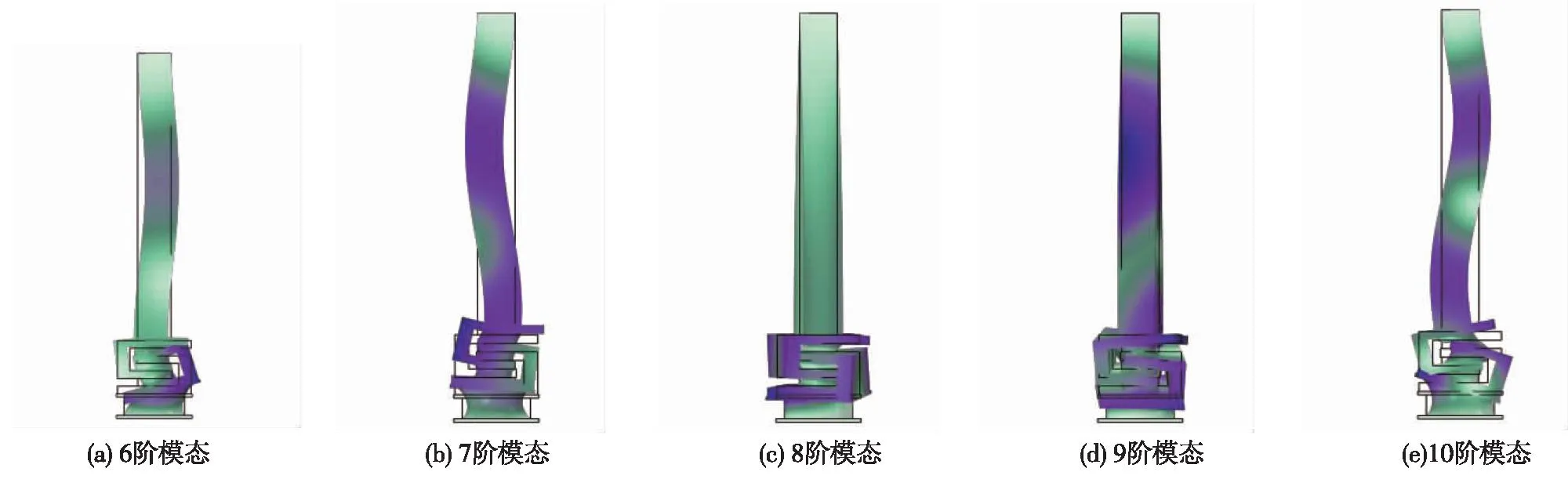
图5 嵌套式隔振柱简化模型后五阶模态Fig.5 Fifth-order modes after simplified modeling of nested vibration isolation columns

简化模型的7阶模态固有频率为54.8 Hz,对应的模态振型如图5(b)所示,振型特征为柱体整体结构失稳。从振型图可以看出,当隔振柱发生该阶模态振动时,柱体结构中部与底部均失稳,异形U状嵌套钢结构上部产生扭转变形。在该阶模态振动下,异形U状嵌套钢结构并未实现良好的隔振效果。

简化模型的8阶模态固有频率为56.5 Hz,对应的模态振型如图5(c)所示,振型特征为柱体结构相对稳定。从振型图可以看出,当隔振柱发生该阶模态振动时,异形U状嵌套钢结构在水平向变形较大,而上部柱体结构保持相对稳定,加速度传递造成的位移偏移较小。因此,在该阶模态振动下,异形U状嵌套钢结构实现了较好的隔振,利用自身变形维持了上部柱体的稳定。

简化模型的9阶模态固有频率为62.5 Hz,对应的模态振型如图5(d)所示。振型特征为柱体结构相对稳定。从振型图可以看出,当隔振柱发生该阶模态振动时,异形U状嵌套钢结构与底部叠层橡胶支座在竖向变形较大,而上部柱体结构保持相对稳定,加速度传递造成的位移偏移较小。因此,在该阶模态振动下,异形U状嵌套钢结构实现了较好的隔振效果,利用自身变形维持了上部柱体的稳定。

简化模型的10阶模态固有频率为76.1 Hz,对应的模态振型如图5(e)所示。振型特征为隔振柱结构整体失稳。从振型图可以看出,当隔振柱发生该阶模态振动时,柱体结构在纵向扭转变形较大,异形U状嵌套钢结构产生倾覆。因此,在该阶模态振动下,异形U状嵌套钢结构并未实现良好的隔振效果。

表4对嵌套隔振柱模态频率及振型特征进行了总结,隔振柱在5个特征频率下实现柱体稳定。

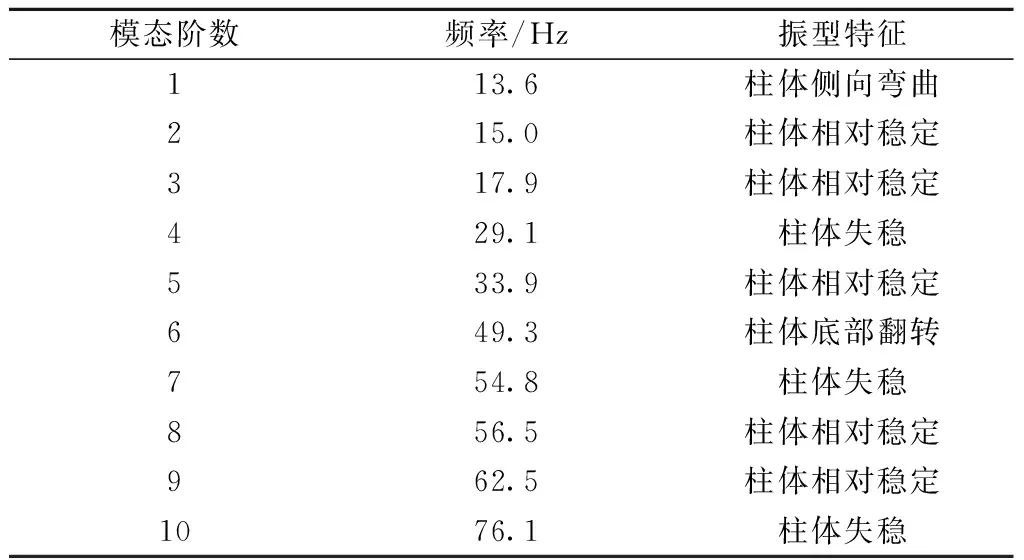
表4 嵌套隔振柱模态频率及振型特征Tab.4 Modal frequency and mode characteristics of nested vibration isolation column

4 频域下加速度传递率分析

4.1 加速度传递率计算方法

定义加速度传递率函数为

661 Prevalence of skin diseases among marine-training soldiers stationed in east coastal area and its influencing factors

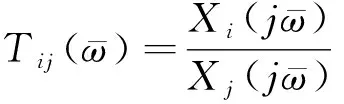
(1)

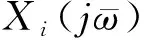
N自由度系统的动力学方程为

(2)

对式(2)作傅氏变换,可得

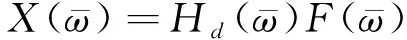
(3)

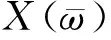
隔振系统所受底部激励向量为

(4)

则隔振系统第i和第j自由度响应分别为

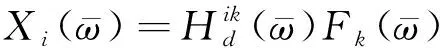
(5)

(6)

响应信号为加速度信号,则式(1)中频响函数为加速度频响函数,系统加速度传递率函数

(7)

4.2 加速度传递率分析

SHENG[18]研究表明,由车辆-轨道系统引起的振动传递至地面时,地面振动频率主要为集中在200 Hz以下的中低频。DING[19]等研究结果表明,车辆-轨道系统引起的荷载传递造成的振动频率一般在1～80 Hz,而引起地面建筑物二次振动的频率与SHENG[20]的研究结果类似,结果为不超过200 Hz的中低频。因此,在频域-加速度传递率分析中主要选取0～200 Hz内频率进行研究。

在隔振柱底部施加1 m/s2加速度,模拟地铁车辆-轨道系统经由土体产生的竖向振动,检验柱体顶面的加速度变化情况。在式(7)的基础上设置对数函数,以比值进行比较,当振动减小时,顶部加速度与底部加速度的比值小于1,在传递函数上的表现为小于零,反之,则大于零,依此函数能够便捷地统计在0～200 Hz频域范围内振动的传递情况。

结合图6并分析可知,将普通隔振柱与嵌套式隔振柱0～200 Hz的加速度传递率进行对比,新式隔振柱在119个频率上有明显的减振效果,即图6中零线下方的点。而普通隔振柱仅在22个频率范围内有减振效果,且其减振频率分布范围集中在175～200 Hz内,在地铁列车运行过程中,不具备很好的减振效果。

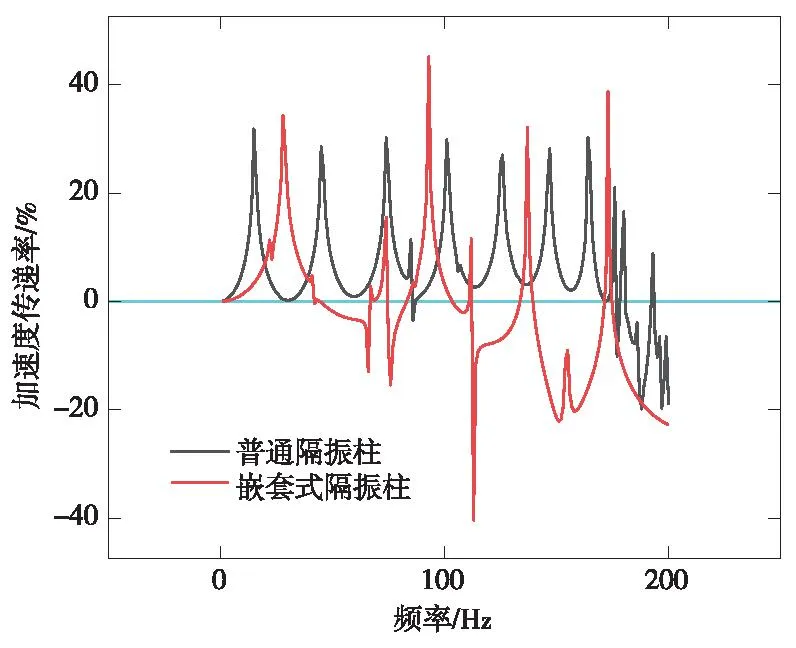
图6 普通隔振柱与嵌套式隔振柱对比Fig.6 Comparison of ordinary vibration isolation columns and nested vibration isolation columns

结合图7并分析可知,在以橡胶减振柱截面直径尺寸为变量的实验中,初始隔振柱模型在119个频率上有减振效果,75%工况在126个频率上有减振效果,而85%工况在130个频率上有隔振效果,较初始模型隔振效果提升了9.2%。

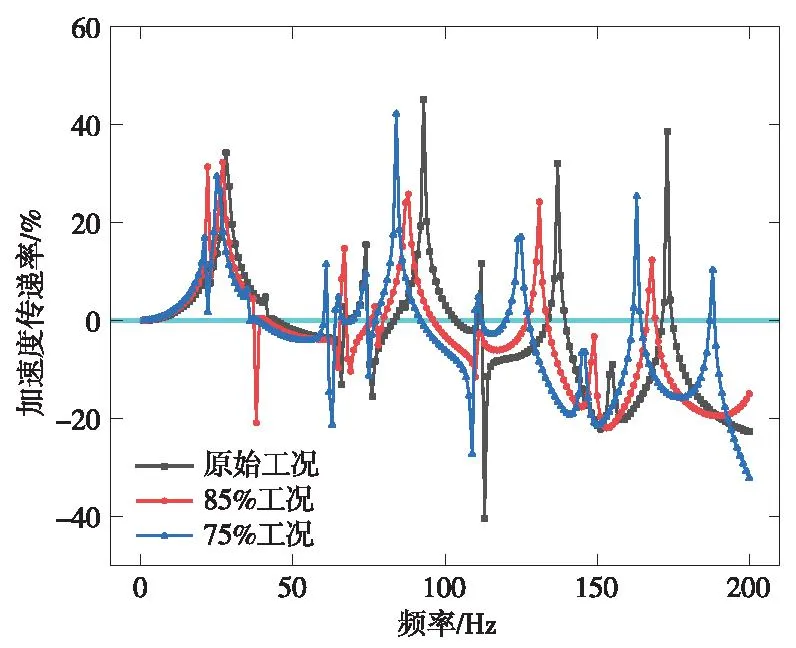
图7 橡胶减振柱直径工况对比Fig.7 Comparison of rubber damping column diameter working conditions

结合图8并分析可知,在以异形U状嵌套钢结构底部平面长宽比为变量的实验中,初始隔振柱模型在119个频率上有减振效果,长宽比为1.1倍工况在120个频率上有减振效果,而长宽比为1.2倍工况在124个频率范围内有明显的减振效果,较初始模型隔振效果提升了4.2%。

图8 长宽比工况对比Fig.8 Aspect ratio comparison

结合图9并分析可知,在以异形U状嵌套钢结构纵向支撑宽度为变量的分析实验中,初始隔振柱模型在119个频率上有减振效果,宽度为1.1倍工况在119个频率上有明显的减振效果,而宽度为1.2倍工况在122个频率上有减振效果,较初始模型隔振效果提升了2.5%。

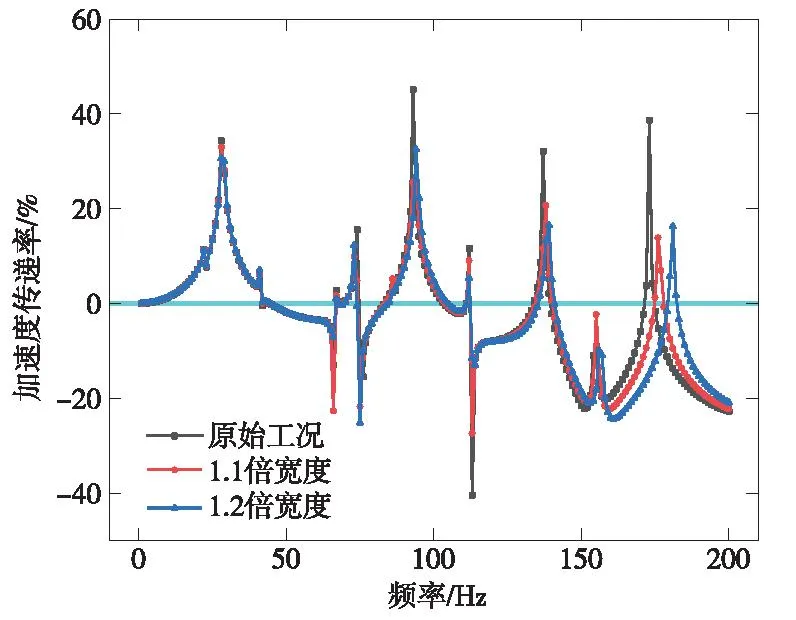
图9 纵向支撑宽度对比Fig.9 Longitudinal support width comparison

5 结论

通过建立地铁车站嵌套式隔振柱的模型,对不同工况进行了模态分析、频域下加速度传递率分析,确定影响地铁车站嵌套式隔振柱隔振性能的因素,主要结论如下。

(1)在普通隔振柱的基础上加设异形U状嵌套钢结构后,隔振柱基频大幅降低,在0～200 Hz的频率范围内实现了60%频率下的竖向隔振,满足地铁车站底部竖向隔振的目的。

(2)在前10阶模态中,设置异形U状嵌套钢结构能使上方柱体结构在5个特征频率下实现相对稳定,达到竖向隔振效果。

(3)适当提高异形U状嵌套钢结构底部长宽比、纵向支撑宽度以及降低橡胶减振体截面直径会带来基频下隔振性能的提升。