隧道纵向开挖变形位移监测数值仿真分析

李江沙，周 荣

(湖北省地质局地球物理勘探大队，湖北 武汉 430056)

0 引 言

隧道在纵向开挖的过程中将会引起地表沉降，进而造成地表建筑物的形变，对人类的生命及财产安全形成较大的威胁，影响整体地表上方正常活动。为此，需对隧道纵向开挖变形位移进行相应监测，提前获取位移信息，避免危险的发生，进一步确保地表及上方建筑物的安全。张英杰[1]基于BIM模型对隧道纵向开挖工程进行实时监控，提升整体监控的有效性，进一步分析隧道纵向形变原因，并分析不同高程和轴向的隧道内部空间网络结构，增强对中心结构数据的调整力度，设置纵向轴网管理变形位移数据，转化标高信息，标记不同区域的位移变化数值，判断区域内部的位移变化程度，标记变化信息，强化对位移数据的精准掌控，提高整体数值仿真分析的精准度，该方法能够同时应用于不同的施工场景，具有较强的可操作性，但对于数值采集的程序较为繁琐，数值分析的效率较低。杨三强等[2]针对隧道开挖过程中的地表形变状态进行数值预测与控制，基于随机介质理论与软件程序编写分析系统，对不同形变产生的位置进行追踪，进一步研究变形区域与隧道挖深之间的关系，匹配关系数值，构建反向传播神经网络，预测隧道断面的变形值，同时离散分析取值信息，调整收缩面积数值，利用滚动预测的方式构建神经网络研究平台，将收集的位移监测数值录入平台中，等待随机处理，该方法具有较高的监测效率，但无法精准获取所需的监测数值，数值仿真的精准度较低。

针对上述问题，本文根据不同区域的隧道变形特征，对其地基结构进行分析，并由此设置数值仿真参数，加强对内部隧道开挖结构的处理力度，调整参数预测信息，提高数据监测的精准程度，进一步强化模型空间构建平台，完善基础数值录入与分析性能，判定位移变形位置，达到信息监测的目的，实现有效的数值仿真分析处理。

1 工程依托

所研究的隧道为城市公路隧道，沿线为城市主要干道路线，隧道中心衬砌管环为预制装配式钢筋混凝土结构，属于浅埋暗挖隧道，采取机械挖掘与预裂挖掘相结合的方式开挖[3]。内部围岩主要组成成分为混合花岗岩，局部区域分布较软岩，岩体整体较为破碎，内部节理裂隙发育，主要结构为破碎状。

对隧道纵向开挖变形位移数据进行监测，并构建仿真模型[4]。在构建模型的初始阶段首先需要设置相应的模型参数，根据隧道开挖的具体特征划分为地基参数与隧道参数，进一步整合参数信息，预测变形位移数据，减少仿真模型构建时的误差，并建立最终的仿真模型，从而实现数值仿真分析。

在距离研究区域西侧150 m处设置5个监测断面(DM-1～DM-5)，每个监测断面的间隔为15 m，分别标记监测点位置(D-1～D-11)，并收集监测点位置信息。在监测断面中存在12个相同的监测点，每个监测点的距离为5 m，其距隧道中心线的距离相等。调整监测断面内部监测点的定位信息，并采用软件程序编写分析系统，利用函数信息对实际测量的地表状态进行数据提取处理，进行相应的仿真分析研究。监测断面及监测点布置见图1，断面监测点布局见图2。

图1 监测断面及监测点布置

图2 断面监测点布局

2 隧道纵向开挖变形位移监测数值仿真模型建立

2.1 地基模型参数构建

在地基模型上添加无法进行压缩的剪切层，同时改善剪切层的土壤信息。考虑土体弹簧之间的相互剪切作用，并配置相关的缺陷检验公式，即

(1)

式中，q为隧道地表上层施加的压力数值；t、u分别为隧道中地基弹簧门限上、下限；D为隧道中地表剪切层的剪切刚度。根据剪切作用分析隧道地表的压力数值，补充隧道外部连接区域的土层信息，设置数据采集平台管理收集的压力数值信息，模拟地基梁信息。针对地基剪力弹簧系数检验变形位移距离，并设置剪力模拟数值验算公式，即

(2)

式中，DF为剪力模拟数值验算值；Ps为隧道中心土层弹性模拟验算值；dp为隧道地基剪切层的厚度；η为隧道地基土层受力比值。按照隧道地面的长梁参数计算地基梁的埋深，进而获取位移的距离参数，考虑地应力之间的平衡，减少建筑物对隧道开挖应力场的影响[5]。整合隧道内部的应力参数信息，估计一定埋深的地基网格数据，判断地基量的基床系数，其计算公式为

(3)

式中，s为基床系数；svesic为基床系数模拟标准参考数值；QI为相关地基网络数据。

为进一步模拟隧道中的土体状态，根据施工方案对隧道内挖掘压力与地表面压力进行测量，去除与隧道地表关系较大的注浆压力值，并在隧道管片中施加顶推力，计算隧道顶推力模拟数值[6-7]。在隧道管片横断面中取得地层损失信息，计算损失系数和隧道地表收缩系数，控制模拟地表缺陷数值，获取地层损失率参数，将其与推荐数值进行对比，并模拟界面收缩率参数。设置相应的土层断面收缩，见图3。图3中，H为隧道顶高；SD为断面收缩损失点；Hg为断面收缩损失点到隧道顶部距离。

图3 隧道开挖断面收缩示意

分析土层中不同微元体的受力状况，并在受力集中区域设置监测点，控制监测点的间距处于相同的数值范围内，微元体受力分析见图4。图4中，Z为顶部受力方向；M为微缘体受力中点；dx为受力范围；Q为剪力夹角。按照分析的受力状态调节地基模型内部结构，并匹配模型简化机制，避免无关因素对整体模型参数构建的影响，完成地基模型参数设置操作。

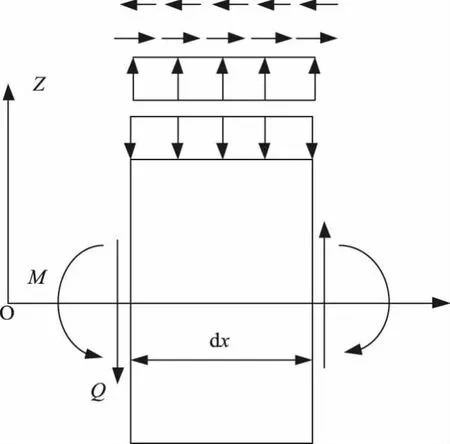
图4 微元体受力分析

2.2 隧道模型参数构建

针对隧道内部结构计算其在开挖过程中的变形与内力，加强对隧道等效弯曲度与剪切刚度数据的收集，并调整不同数据存储的空间位置，简化模型计算程序，在横向修正惯数的条件下处理横向刚度变化参数，设置等效抗弯刚度计算公式，即

(4)

式中，Erp为等效抗弯刚度；Eb为隧道中管片弹性模量；m为隧道纵向开挖过程中使用的螺栓总体个数；Ha为隧道纵向平均线高度数值；ks为螺栓相应长度数值；FD1为隧道横断面受力数据。

根据隧道中不同区域的土质分布情况分析地表沉降状态，并记录沉降数值[8]。在地层中构建整体大地坐标系，加强对隧道内部中心结构的控制，同时管理地表隧道之间的土壤湿度参数，计算管片混凝土的弹性模量，并集中收集隧道中心区域的地层影响角数值[9]。在土体中设置三角单元，计算单元体与开挖变形中心区域的距离。控制不同影响角的设置高度，调节中心角的位置，计算此时位移土层的等效剪切刚度，并设置其表达式，即

(5)

式中，Aϑrp为位移土层的等效剪切刚度；ξ为隧道内部开挖结构经过修正的摩擦系数；Ds为隧道中心螺栓剪切模量；Es为管片环剪切系数；ϑ为隧道中管片剪切模量。将经过剪切处理的隧道模型参数进行土层状态分析，对隧道断面收缩不均匀状况进行调整。不均匀收缩示意见图5。图5中，a～g为设置的7个隧道断面不均匀收缩监测点；x为隧道水平位面；R为点f到点d之间的收缩夹角。调整断面收缩范围，得到所需的隧道模型参数。

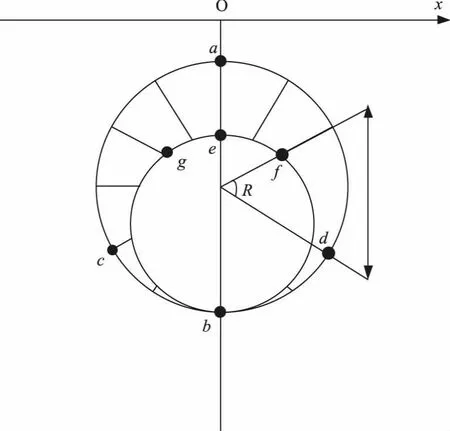
图5 隧道断面不均匀收缩

2.3 开挖变形位移数据预测

在获取仿真参数的基础上，对隧道开挖变形位移数据进行预测处理，判断位移产生的位置范围，同时设定位置检测参数并对其进行集中调整[10]。模拟不同区域的位移信息采用BP神经网络对预测数据进行训练处理，设置训练目标最小误差数值，并将其组合成训练样本[11]。预测实际位移数据与设置数据之间的差异，采用网络相关系数评价构建的预测模型，并设置其位移系数评价公式，即

(6)

式中，S为位移系数评价等级；Wi为不同数据之间的误差参数；N为评价门限；i为评价初始数值。经过系数评价后，调节不同预测参数之间的匹配关系信息，并加强对训练集的集中处理，简化内部处理操作，缩短预测时间，提升整体仿真分析的效率。进一步计算平均评价数值，其计算公式为

(7)

式中，Se为位移平均评价数值；M为训练集中的数据总量。调整预测数据的位置信息，同时针对隧道开挖过程中产生形变的位置变化状态进行标记处理。描述地表沉降相对间距参数，设置临界值，将该值作为预测训练集与实际数据集合之间的距离远近的判断依据，其临界判断公式为

(8)

式中，Q为断面纵向收缩临界值；I为隧道内部轴线间距数值；n为隧道开挖过程中地表沉降槽水平宽度临界值；Z为相关地表沉降槽宽度参数；O为隧道开挖深度；λ为隧道土体内部摩擦角系数。在计算临界数值后，分析土体附加应力，获取所需的预测参数，由此实现开挖变形位移数据的预测处理。土体附加应力分析见图6。图6中，A为断面纵向2个监测点Z1、Z2的土体应力夹角；B为断面水平2个监测点X1、X2的土体应力夹角。

2.4 数值仿真模型构建

将预测的数据集中收录至仿真模型构建系统中等待模型建立[12]。将数据划分为多个不同的仿真微元体进行数据拟合处理[13-15]。标记地层整体坐标，并对隧道开挖时的地表整体沉降状态进行仿真模拟，设置其模拟公式，即

(9)

式中，I(X)为隧道开挖时的地表整体沉降状态的仿真模拟数值；α为隧道开挖地层影响角数据；μ为设置的数据体集合距地表中心的距离数据；ζ为隧道中心距离宽度参数；R为隧道中心沉降水平距离参数；d为隧道直径。经过模拟后调整不同区域土体的挖掘状态，并加强对中心隧道结构的数据调节处理，拟合隧道挖掘变形位移状况，并提取隧道中开挖施工相互作用影响信息。内部施工相互作用影响见图7。

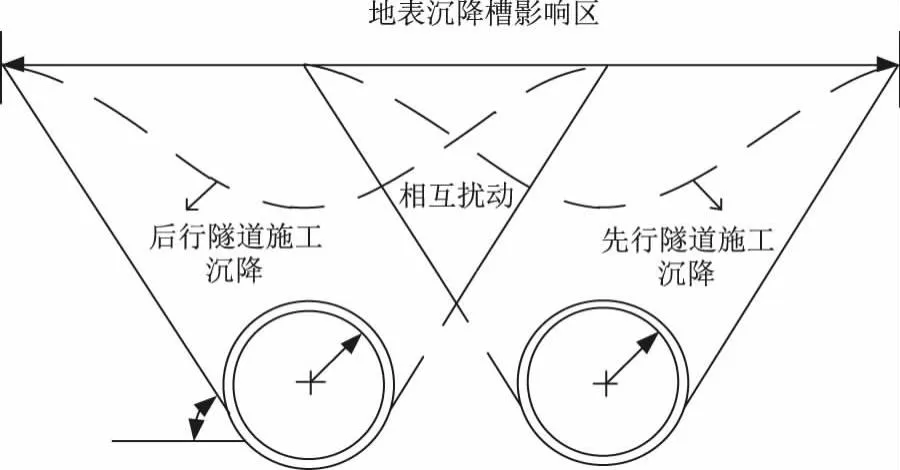
图7 隧道开挖相互作用影响

根据影响信息匹配仿真参数，同时监测隧道土体与表层墙体之间的扰动关系，标记沉降点信息，构建扰动比值计算公式，即

(10)

3 数值仿真结果分析

3.1 隧道地表沉降

为有效验证研究方法监测的有效性，对数值仿真进行相应的数据对比处理，将不同方法得到的地表沉降数值与实际测量数值进行比较，并分析其比较结果。不同方法地表沉降数值结果见图8。从图8可知，当距隧道中线距离为0时，实际监测的地表沉降数值为-0.014 5 m，本文方法为-0.014 6 m，基于BIM模型方法为-0.012 5 m，基于随机介质理论方法为-0.012 m。由此可知，本文方法地表沉降数值与实际监测数值之间的差异最小，整体误差率为0.005%，具有良好的监测效果。

图8 不同方法地表沉降数值对比

3.2 隧道隆起

为进一步验证不同方法数值仿真分析的精确度，对隧道隆起变形进行对比分析。不同方法得到的隧道隆起变形对比见图9。从图9可知，本文方法隧道纵向开挖变形位移的隆起数值变化曲线与实测值相一致。当隧道于基坑中心距离为0时，实测隧道隆起数值为2.6 mm，本文方法为2.7 mm，基于BIM模型方法为2.9 mm，基于随机介质理论方法为2.0 mm。由此可知，所研究方法的隧道隆起数值与实测值的差距最小，整体误差率为0.001%，能够有效监测隧道纵向开挖造成的变形位移，具有良好的分析效果。

图9 不同方法隧道隆起变形结果对比

4 结 语

本文针对隧道纵向开挖变形位移进行监测数值仿真分析，在获取变形位移数据的基础上设置相应的仿真模型参数，构建模型数据，以达到精准监测位移数据的目的，得到以下结论：

(1)由于隧道地表的变形主要呈现反对称分布状态，其变化大小随着地层的深度而变化，在实际监测的过程中需加强对中心区域的结构化处理，避免地层数据对仿真结果的影响。

(2)在进行变形位移数据采集的同时，需时刻监控地表参数的变化状况，发生不良反应时及时进行数据收录处理，避免无关因素的影响，进而提升整体研究的精准度。

(3)在掌控隧道特征信息的基础上进行数值仿真能有效提升仿真的效率，并获取可靠度较高的仿真数值，提升了数值仿真的科学性。