基于MIQP-GWO的水火风光近似区间需求响应调度

陈 晨，丁 武，罗景镇，康传雄

(1.水电水利规划设计总院，北京 100120；2.水电水利规划设计总院有限公司，北京 100120；3.珠江水利科学研究院，广东 广州 510611；4.华中科技大学土木与水利工程学院，湖北 武汉 430074；5.南昌工程学院水利与生态工程学院，江西 南昌 330099)

0 引 言

随着新能源规模化接入电网，未来电网将呈现显著的“双侧随机性”，源网荷之间将形成更加“互动”的模式，构成形式和交互模式也较目前电网也将更趋复杂。为了更好的应对风电和光电的不确定性，充分发挥梯级水电、火电的调节能力，开展多种能源的联合优化调度，构建适应新能源占比逐渐提高的新型电力系统，已经成为当前电网调度亟需解决的问题。

区间方法建立在区间算法的基础之上[1]，Moore针对计算机数值截断误差的问题，提出了区间数的概念[2]，并引入到现代数值分析中[3]，随后人们对区间模型的理论和应用进行了大量的研究[4]。区间算法的一个重要功能是计算区间函数值包含区间，因此区间函数也称为扩张函数。区间算法能够快速地计算出函数值域的包含区间，但是这个包含区间可能比实际区间放大很多，因此需要将区间算法进行适当调整。目前用于计算区间函数值的扩张函数主要包括自然扩张函数、中心扩张函数和Taylor扩张函数[5-7]，文献[2]指出，如果函数表达式中每个区间变量只出现一次，则自然扩张函数计算所得区间不会被放大，但是大多数函数无法表示为每个区间变量只出现一次的形式。文献[3]对这3种扩张函数进行了比较，结果显示在大多数情况下，Taylor扩张函数将得到最窄的区间，即区间被放大量最小，而中心扩张函数则在区间变量的变化范围比较大时才会比自然扩张函数更有效。文献[8]指出对非单调函数，契比雪夫扩张函数比传统的泰勒扩张函数能更有效地控制区间算法的“包裹效应”。

在应用区间变量求解问题的过程中，区间变量往往通过区间数序关系或最大最小后悔准则将不确定性优化问题转换为确定性优化问题进行求解。通过引入区间数序关系，Tanaka[9]，Rommelfanger[10]和Ishibuchi[11]将区间数优化转换为确定性的参数进行规划求解。文献[12-14]通过序关系的满足程度将区间约束转换为确定性约束进行求解。文献[15]在多种区间可能度之间的关系基础上给出了区间数排序的可能度法来求解不确定多属性决策的方案排序问题。姜潮针对一般的不确定性优化问题，提出了区间序关系转换模型和区间可能度转换模型这两种模型，从而将不确定优化问题转换为确定性优化问题[16]。赵子衡针对区间不确定优化中内层优化的极值性要求问题，提出了基于代理模型的全局搜索策略，提高了区间算法在求解强非线性的复杂系统不确定优化问题时的效率[17]。Zhang等人利用区间仿射技术将区间优化方法应用到区间潮流问题解决中，并取得了一定的成果[18]。

电力系统优化调度通常要求在满足一系列实际约束的前提下，在调度期内的每个时段为各火电站分配负荷以及为各水电站安排发电流量从而实现系统效益最大化。本文提出一种基于实时电价需求响应的风光出力不确定区间调度模型，并提出一种嵌套混合整数二次规划的灰狼算法(MIQP-GWO)优化求解该模型。本文首先通过切比雪夫区间扩张函数求解得风光出力的精确近似区间，然后通过启发式方法将包含区间变量的目标函数与约束转化为确定性的目标函数与约束，再通过启发式的确定性算法，基于火电最低成本对火电站间进行负荷分配。最后通过算例对提出的区间需求响应调度模型以及MIQP-GWO算法的性能进行了测试，并将所得结果与其他单目标启发式方法求解区间需求响应调度模型的结果进行了对比。结果表明本章中提出的调度模型结合MIQP-GWO算法求解效益问题的可行性与稳定性。

1 基于电价不确定性的水火风光区间联合调度模型

1.1 基于供给侧的电力售价需求弹性模型

需求响应是一种用于激励终端用户根据电力出售价格随时间的变化而进行的用电变化。为了评估客户参与需求响应模型对电力系统负荷特征的影响，有必要开发响应式负荷经济模型。在这个模型中，客户可以根据实时的电力价格调整他们的需求，与此同时，电力价格将实时更新，以考虑这些负荷的调整变化，存在彼此之间相互影响、相互制约的关系。典型的电力售价—需求关系如图1所示。

图1 电价—需求曲线及其时段线性化处理

可以根据每个调度时段的负荷情况在其附近将图1所示的电力售价—需求曲线进行截取，本文采用已知每个时段的负荷预测值D0以及与其对应的电力价格ρ0作为基准点(D0，ρ0)，以基准点为中点、以电力供应商确定的价格对负荷的可调控区间作为响应负荷的上下限，截取电力售价—需求曲线以获得每个调度时段初始的电力售价—需求曲线，得到初始电力售价—需求曲线后，为了简化计算以及方便建立基于价格弹性的需求响应模型，可将初始曲线线性化处理，得到每个调度时段的电力售价—需求关系曲线。

每个调度时段的电力售价—需求关系确定之后，基于电力售价—需求弹性建立实时定价的电力售价需求响应模型。需求的价格弹性系数定义为线性化的电价—需求模型的相对斜率，即电力需求对电力售价定位的敏感度。由于每个时段的电力售价—需求关系是单独线性化处理的，本文认为每个时段的需求响应是完全独立的，各时段不同电价下消费者的响应表达式和约束可以描述为

(1)

Dt，min≤Dt≤Dt，max

(2)

式中，εt为t时段的价格弹性系数；Dt为电力供应商调整电价后的消费者的负荷需求；Dt，0为电力供应商所预测的t时段消费者的负荷需求；ρt为电力供应商经调整后的电价；ρt，0为t时段预测负荷所对应的基准电价；Dt，min为响应负荷的下限；Dt，max为响应负荷的上限。响应负荷的上下限的制定一定程度制约电力供应商为了追求利益最大化而一味调控出力破坏电力市场机制。根据式(1)，调整电价后消费者的负荷需求Dt为

(3)

式中，Dt为调整电价后t时段消费者的负荷需求。

本文选取Dt，0的±15%作为响应负荷容量，即Dt，min=0.85Dt，0作为响应负荷的下限，Dt，max=1.15Dt，0作为响应负荷的上限。由上述线性化的价格—需求模型可知，Dt，min对应电价的上限ρt，max，Dt，max对应电价的下限ρt，min，由此可求得每个时段电价的上下限。通过求得调度期内每个时段电价的可调范围，电力供应商可以根据各时段的电价上下限建立优化模型，从而实现电力系统的效益最大化。

1.2 水火风光区间需求响应调度模型

本文选取电厂效益最大以及发电成本最小作为经济调度原则，结合实时定价的电力售价需求响应模型，将不确定性的风、光新能源并入系统以及对负荷进行爬坡限制建立区间优化调度模型。在此模型中，由价格需求弹性模型，电力供应商对每个时段的电价进行调整设计，以引导消费者用电行为从而得到新的负荷曲线，基于此再对水、火电厂进行最优负荷分配，考虑到风、光出力皆为不确定性的区间变量，模型中的总效益与总的发电成本亦皆为区间数，具体的数学模型如下。

发电厂的效益可由售电收入减去发电总成本，其目标函数可表示为

(4)

式中，T为调度期内总时段；FI为调度期内电力系统发电总成本。电力系统中各部分的发电成本可由其出力乘以其对应发电成本系数给出

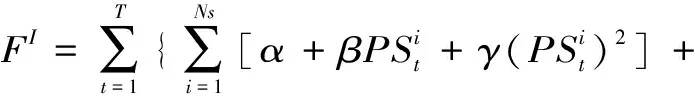
(5)

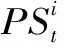
模型需考虑的约束条件如下：

(1)系统总负荷平衡约束

(6)

(2)负荷爬坡率约束

-Dsc≤Dt-Dt-1≤Asc

(7)

式中，Asc、Dsc分别为每个调度时段内负荷的最大升值、降值。

(3)水电出力关系

(8)

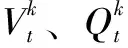
(4)火电出力限制

(9)

式中，minPSi、maxPSi分别为第i个火电厂的出力下限和上限。

(5)水库库容约束

(10)

式中，minVk、maxVk分别为水库k的库容下限和上限。

(6)水库发电流量约束

(11)

式中，minQk、maxQk分别为水库k的发电流量下限和上限。

(7)水库水量动态平衡约束

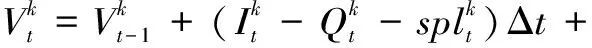
(12)

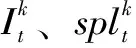
(8)水库初末库容约束

(13)

(14)

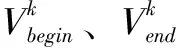
(9)电价上下限约束

ρt，min≤ρt≤ρt，max

(15)

式中，ρt，min为t时段电价的下限；ρt，max为t时段电价的上限。

2 MIQP-GWO算法及需求响应区间调度求解过程

灰狼算法(GWO)模拟了灰狼在自然界中的领导层次和狩猎机制，GWO算法具有结构简单、需要调节的参数少、容易实现等特点，其中存在能够自适应调整的收敛因子以及信息反馈机制，能够在局部寻优与全局搜索之间实现平衡，因此在对问题的求解精度和收敛速度方面都有良好的性能。

由于标准的GWO算法是针对无约束单目标优化问题而开发的，对于水火风光区间调度中高维度、复杂、强耦合的非线性约束缺乏有效的处理方式。为此，本文提出一种MIQP-GWO算法，引入确定性算法计算调度期内各时段每个火电站出力使其出力总成本最低，并将水电站发电流量修正到可行范围内使其满足水库调度约束，这些启发式的约束处理策略有效的提高了寻优效率。

2.1 区间目标函数转换和约束处理策略

2.1.1 区间目标函数转换

区间优化调度模型的目标函数包含了区间变量，在处理目标函数时无法直接判断其优劣次序，本文采用区间的中点与半径来衡量，对于本文的目标函数，可将其转化为最小化问题：

(16)

其中目标函数的上下限P.r和P.l可分别表示为

(17)

(18)

由此可求得目标函数区间的中点和半径

(19)

(20)

即可将区间目标函数转换为如下的确定性多目标优化问题

min{P.c，P.w}

(21)

为进一步简化，本文采用线性加权法将上述多目标优化问题转化为单目标模型

(22)

式中，fd(x)为多目标评价函数；β为多目标权系数，0≤β≤1；ξ为保证P.c+ξ、P.w+ξ为非负的参数；φ、Ψ为多目标函数的正则化因子。

2.1.2 启发式区间负荷平衡约束处理

含有区间变量的约束函数无法有效的表达成为确定性的约束关系，为了将区间定量化，采用概率表示的方法定量地判断一个区间与另一个区间的大小关系。在用概率表达的形式量化各区间之间的大小关系之后，进而引入“区间置信水平”的概念，即使得区间不确定约束在某一可能度水平下得以满足，进而将区间不确定约束函数g(x，u)≥aj转化为确定性不等式约束P(gI(x)≥aj)≥λ。其中λ∈[0，1]为一预先给定的区间置信水平，gI(x)∈[gl(x)，gr(x)]。本文采用区间扩张函数得到风、光出力近似区间，并按照“区间置信水平”的概念可将其转换为

(23)

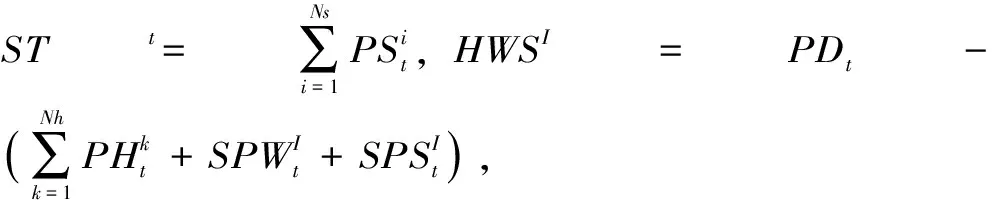
(24)

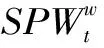
2.1.3 基于MIQP的火电负荷分配

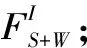
(25)

(26)

2.2 基于MIQP-GWO求解基于需求响应的水火风光区间调度流程

下面给出MIQP-GWO求解基于需求响应的水火风光区间调度模型的详细应用步骤：

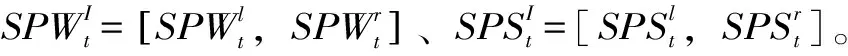
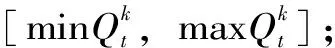
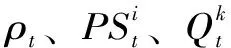
(4)基于各时段电价ρt通过需求响应模型计算出各时段的负荷需求Dt，利用启发式的水库库容约束策略调整水库发电流量，应用启发式的区间负荷平衡约束处理策略求得火电总出力STt。

(5)由各时段火电总出力与各火电站额定总出力上下限建模，基于MIQP使成本最小的火电站负荷分配策略对各火电站出力进行调整。经过各项调整后得到新的种群invi。

(6)通过区间序关系对区间目标函数进行转换，并求解出种群中各个体的适应度值，按照适应度值对种群进行排列，然后按照GWO算法的狩猎、寻找猎物、包围猎物和攻击猎物4个主要流程进行计算。

(7)如果达到最大迭代次数Maxiter，转到下一步；否则重复步骤4～6，直到达到最大迭代次数。

(8)选出最终种群中的适应度值最高的解，为最优解集。输出结果为调度期各时段的电价、水电站计划发电流量，各火电站时段出力和电力系统的总发电利润。

3 仿真实例分析

3.1 算例描述

本文应用一个带风、光电的水火电力系统的日调度模型来验证MIQP-GWO算法解决水火风光联合区间调度问题的性能。该系统包含4个梯级相连的水电站，8个火电站，20个风电机组，50 000 m2的光伏出力场。该问题的调度周期为1 d，分为24个时段。系统24 h总负荷预测如表1所示。

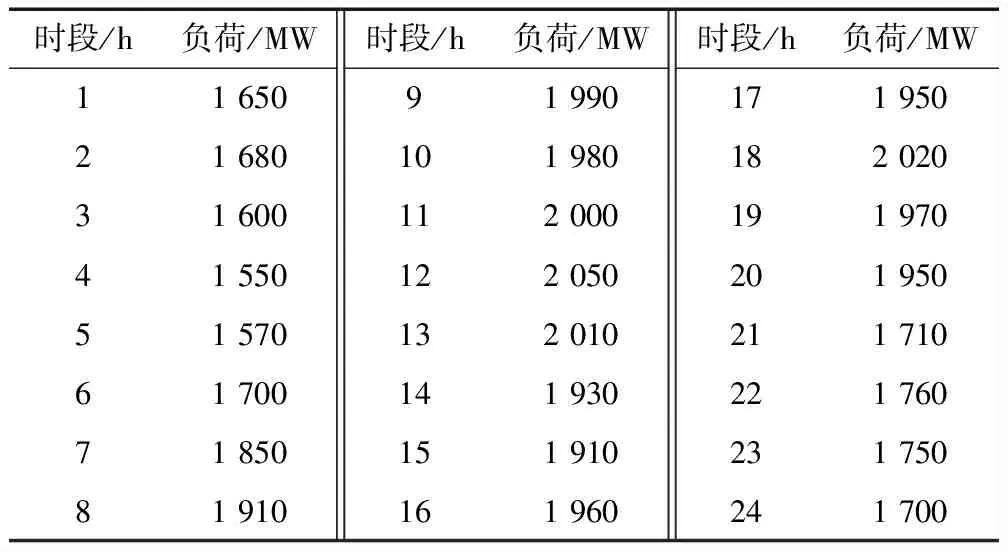
表1 系统24 h总负荷

3.2 参数设置

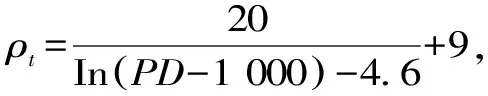
3.3 计算结果对比

由于这3种算法在产生初始种群时具有随机性，所以为了消除随机性的影响，本文独立运行这3种算法各10次，计算结果记录如图2所示，取这10次中每种算法的最好结果作为水火风光联合区间调度问题的最优解。

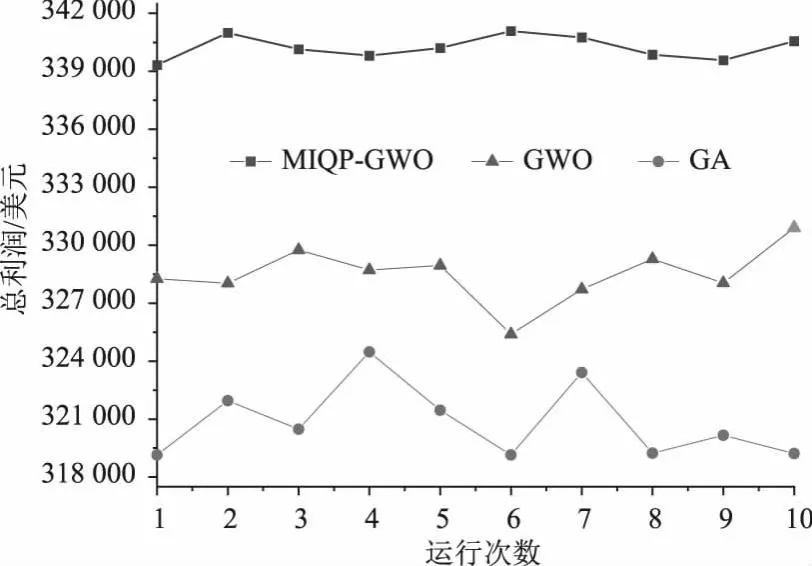
图2 3种算法10次独立计算的结果收益对比

由图2可以看出，3种方法计算得到的最优解中，MIQP-GWO的优化结果都远远优于其他2个算法，可以得出在处理水火风光区间联合调度问题时，MIQP-GWO的效果好于GA和GWO。为了更加直观的说明MIQP-GWO算法的优越性，本文使用标准差与算法计算所得最大最小值作为每种算法的性能指标，对3种算法进行比较，每种算法的性能指标的结果如表2所示。

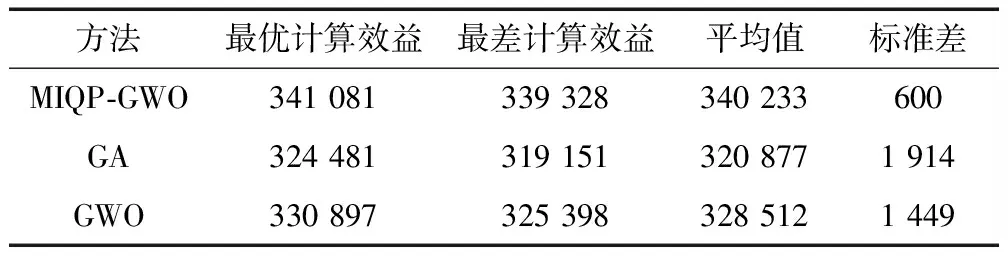
表2 3种方法的性能指标比较 美元

由表2可知，MIQP-GWO算法对于优化求解风光水火区间联合调度问题的绝对优势，其计算所得的最差效益都比GA与GWO的计算所得最优效益要好，且通过对其平均值与标准差进计算，得出MIQP-GWO所计算的结果具有非常好的性能和稳定性，这在工程中具有较好的实用价值。下面选取MIQP-GWO所计算的结果中最好的一次(第6次)进行具体分析，其结果如图3～7所示。

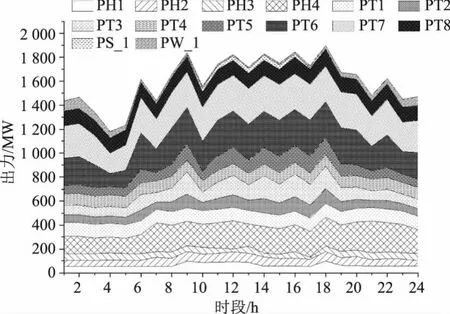
图3 系统出力下限

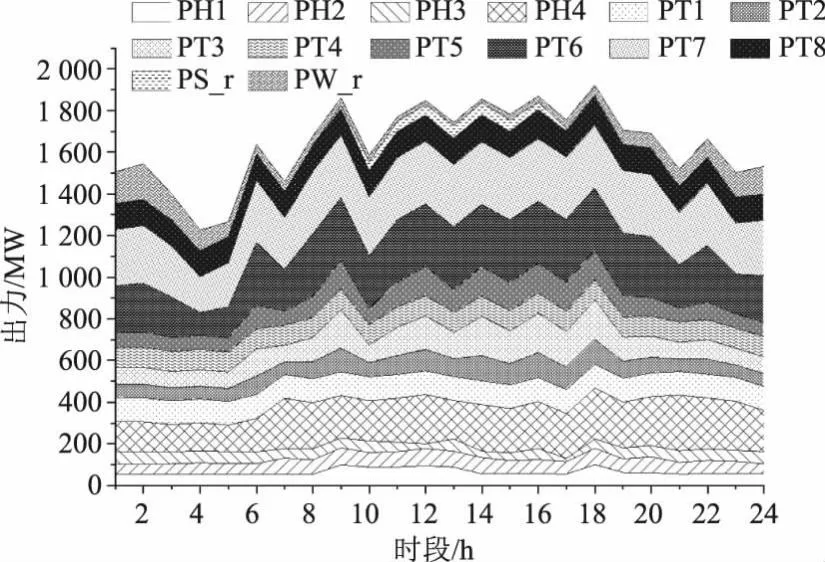
图4 系统出力上限

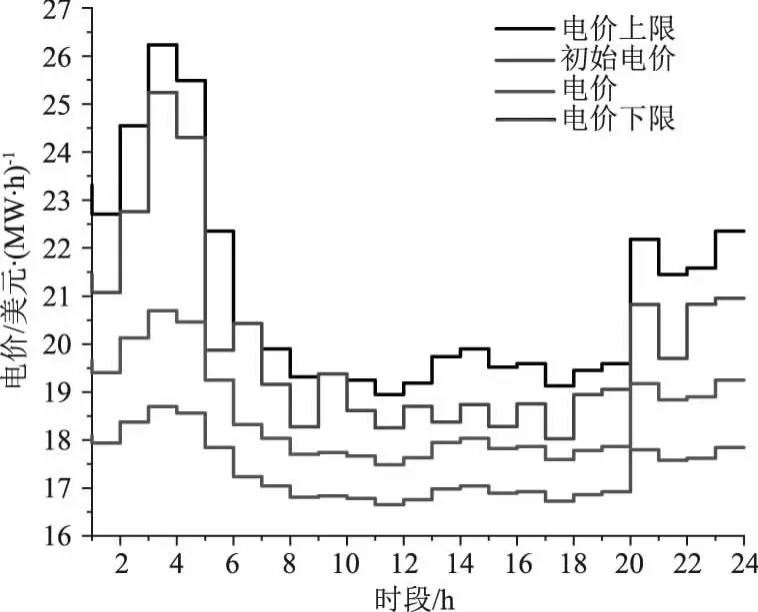
图5 时段电价曲线

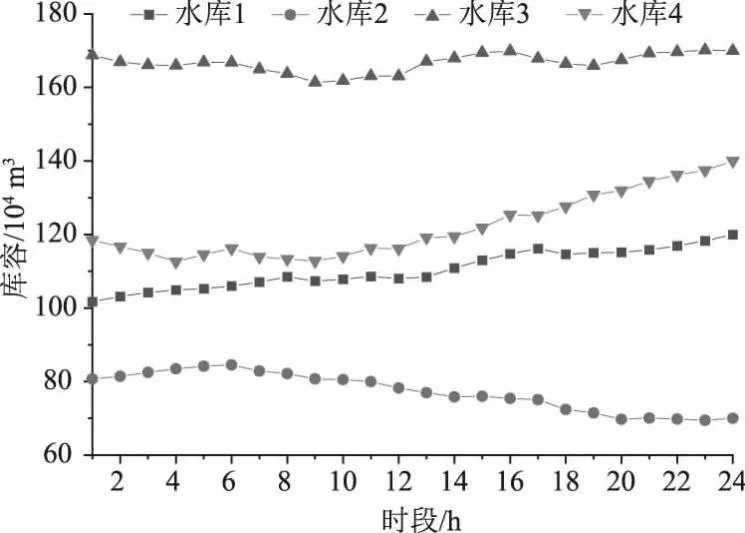
图6 水库时段库容变化过程

由图3～7可以看出，所有火电厂出力、水电站发电流量和水库库容均处于约束范围内，调度时期的末库容也符合末库容约束，电价也在负荷电价区间，所以计算所得解是可行解。

由此可见，将需求响应与资源规划相结合，实现需求响应的全方位影响，实现效益的最大化，这些努力有助于建立对需求响应的短期和长期价值和贡献的期望，需求响应计划经理和监督人员能够可靠地衡量电力系统的净效益，以确保它们能有效地提供所需的需求减少和成本效益方面。同时，从图7可知，相对于客户的原负荷，经过调度后负载在各时段都有所下降，即需求响应导致了批发市场电力售价的下降，从而降低了零售商的供应成本，并最终使几乎所有零售客户都能享受到电力售价的优惠。

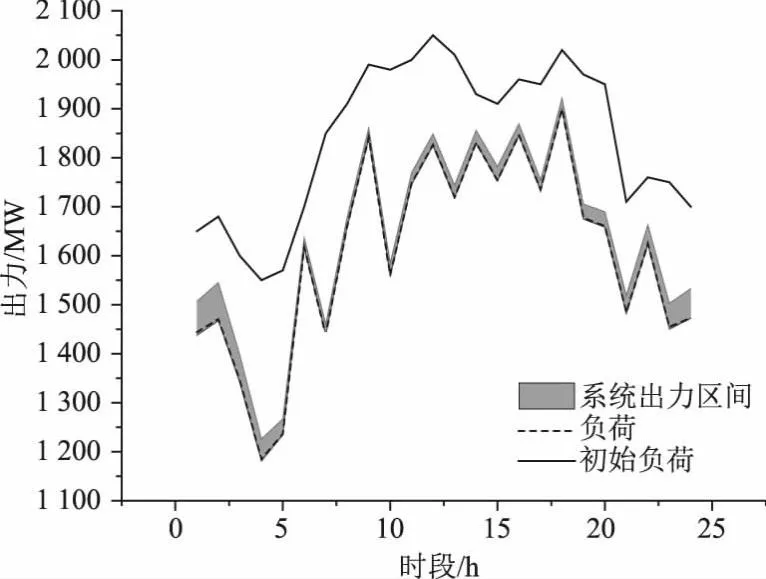
图7 系统负荷与区间出力曲线

4 结 语

本文对短期水火风光区间联合调度问题进行了探索。首先以电力系统发电效益最大作为经济调度原则，结合价格弹性的用户需求响应模型，将不确定性的风、光新能源并入系统建立区间优化调度模型，然后利用契比雪夫扩张函数计算出不确定性的风、光出力区间。本文在原始的灰狼算法(GWO)的基础上，嵌入确定性算法，并采用启发式的约束处理策略，将其改进为可求解区间单目标问题的区间灰狼算法(MIQP-GWO)。最后，本文应用一个含有四个梯级水电站、八个火电站、一个大型风场和一个大型光电场来验证MIQP-GWO算法解决该类区间单目标问题的能力。同时，还利用两种区间单目标算法(GA和GWO)与MIQP-GWO算法进行对比，由对比结果可知，MIQP-GWO算法的性能要远远优于其他两种算法的性能，可以得到效益更大，计算结果更稳定的最优解。因此，可以说，MIQP-GWO算法在解决水火风光单目标区间联合调度问题时有着优秀的表现，可以为决策者提供较为优秀可靠的决策方案。