基于最优经济效益的虚拟电厂平台优化调度模型
2024-02-26黄宸希吴雪琼冯荣强黄晓铭
黄宸希,吴雪琼,冯荣强,黄晓铭,唐 伟,夏 栋
(1.南瑞集团公司(国网电力科学研究院),江苏 南京 211100;2.国电南瑞南京控制系统有限公司,江苏 南京 211100)
0 引 言
虚拟电厂(Virtual power plant,VPP)通过将多种分布式资源聚合成一个发电整体可向大电网提供发电计划及负荷需求,为分布式资源并入电网提供可靠的方法[1-2]。
文献[3]提岀了一种含有需求响应VPP的风电并网模型,通过建立激励型需求响应VPP模型增强系统调度的灵活性,提高新能源的消纳。文献[4]提出了一种关于需求侧响应的虚拟电厂模型,其以系统运行成本最低为目标,建立了关于需求侧响应的虚拟电厂优化调度模型。文献[5]提出一种分布式风电和储能构成虚拟电厂参与电力系统优化调度模型,并通过相关方法进行验证。文献[6]提出了一种含电动汽车的虚拟电厂优化调度模型,通过考虑电动汽车的时空分布特性,以EVPP综合收益最大化与申报偏差率最小化构建了EVPP调度优化模型。文献[7]提出了一种基于分时电价的虚拟电厂双层优化调度模型,通过运行方式的改变使虚拟收益最大。文献[8]提出一种考虑虚拟电厂的碳成本与用户侧需求响应,构建含虚拟电厂之间功率交互的经济调度策略。以上研究大多是基于单一分布式资源的虚拟电厂的优化模型,未考虑在多因素作用下的VPP优化调度模型。本文以VPP经济效益最优为出发点,提出了一种含分布式储能、风电及需求侧响应的VPP最优调度模型,根据电力市场需求响应信息、分布式资源的日前出力预测、协调虚拟电厂各发电单元的运行策略降低其预测出力与实际出力之间的偏差,使得VPP收益最大。
1 虚拟电厂最优调度策略
本文以VPP经济效益最优为目标,通过构建VPP最优调度运行策略,协调VPP各发电单元出力情况,降低VPP预测出力与实际出力的偏出,使得VPP经济效益最大。虚拟电厂最优调度流程(见图1)包括以下4个步骤:
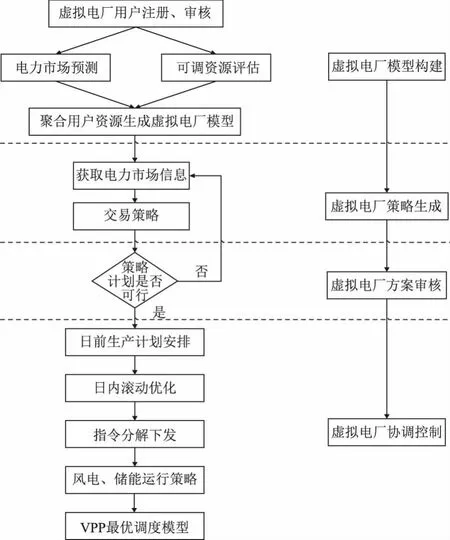
图1 VPP最优调度流程
(1)虚拟电厂模型构建。虚拟电厂根据接收注册的用户信息及电力市场的预测情况,整合用户的可调资源,将不同用户下属的各种分布式资源进行聚合,生成对应的虚拟电厂模型。
(2)虚拟电厂策略生成。虚拟电厂根据电力市场基本信息生成对应交易策略,并提交相关运行调度信息。同时接受市场出新结果进行日前计划生产安排。
(3)虚拟电厂方案审核。将日前计划生产安排提交调度审核,根据审核结果进行日前生产计划安排、日内滚动优化调整及指令下发,通过指令下发进行分布式资源的协调控制。
(4)虚拟电厂协调控制。根据分布式资源的实时出力情况,动态调整VPP各分布式资源运行策略,使得VPP的预测出力情况与实际出力情况偏差最小,生成VPP最优调度模型。
2 虚拟电厂最优调度模型构建
本文通过构建各发电单元出力模型,VPP模型约束条件,实现VPP经济效益最优化。VPP基于各类分布式资源的出力预测,实际出力情况,协调各类分布式资源的出力,使得VPP的预测出力与实际出力偏差最小,效益最优。
2.1 虚拟电厂可调资源评估模型构建
2.1.1 风电出力模型
风电出力情况主要取决于输入风速和光照强度,因此其出力模型可表示为
(1)
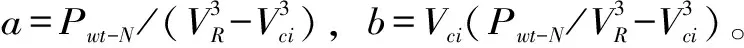
风力发电的总成本为
(2)
式中,Cwt为风机出力的总运行成本;cwt为风力发电的单一运行成本;M为风力发电机组的总个数。
2.1.2 储能出力模型
由于储能自身具有充放电能力,其出力不受外界环境的影响,分布式储能出力模型可表示为
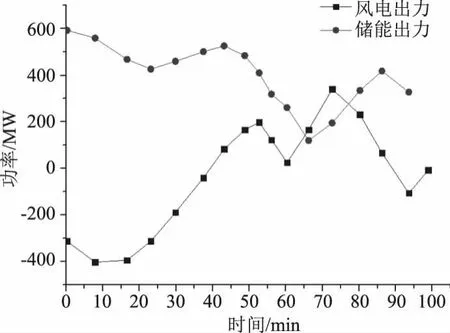
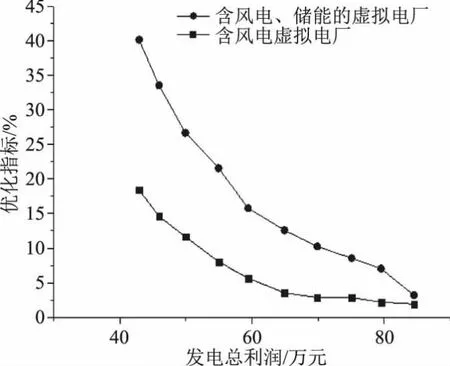
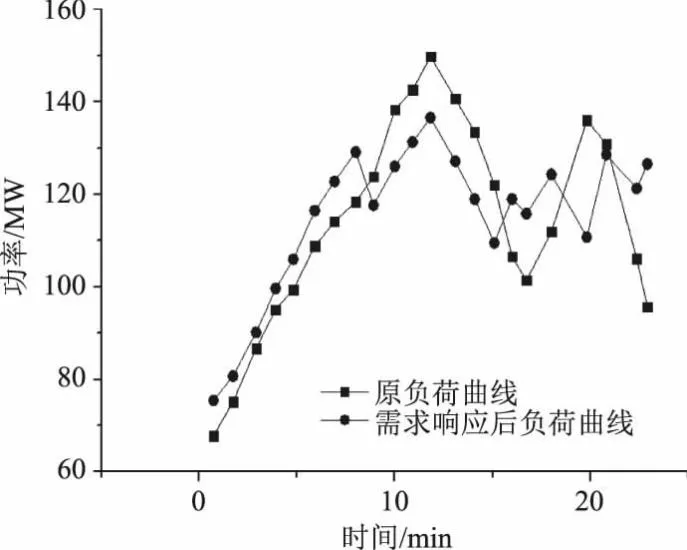
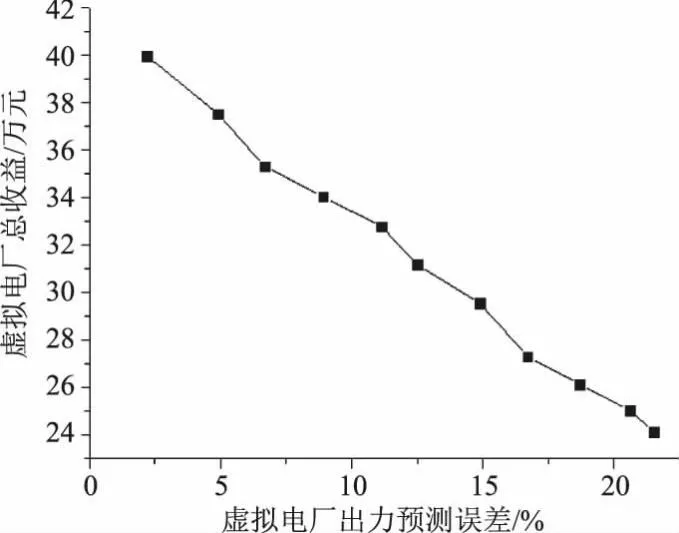
-Pn,max (3) 式中,Pn,ES(t)为第n个储能设备在t时刻的出力;Pn,max为储能的最大出力。 储能的总成本为 (4) 式中,CES为储能的出力的总成本;cES为单个储能设备的出力情况。 由于VPP由多种分布式资源构成,因此在VPP接入电网侧需要满足电网对于分布式资源接入的要求及分布式资源自身的约束。 (1)有功功率平衡约束 (5) (2)潮流约束 (6) (3)风电机组的出力约束 PW≤Pw (7) 式中,Pw为风电的预测出力;PW为风电实际出力。 (4)储能设备充放电约束 0≤pesc(t)≤pesc,max (8) 0≤pesd(t)≤pesd,max (9) Ssocmin≤Sscot≤Ssocmax (10) 式中,Pesc(t)、Pesd(t)分别为储能设备t时间段内充、放电功率;pescmax为储能设备充电功率的最大值;Pesd,max为储能设备放电功率的最大值;Ssocmin为储能设备的最小剩余容量;Ssocmax为储能设备的最大剩余容量。 基于分布式资源及电网侧的各类约束条件构建虚拟电厂最优调度模型,通过考虑、需求响应、风电、储能出力等多种因素,降低VPP预计出力与实际出力的偏差,实现VPP收益最大化。 (1)虚拟电厂的目标函数 (11) (12) 式中,Rload(t)为t时段内虚拟电厂响应基于价格型的需求响应获利情况;Rwind(t)为t时段内风电机组的收益情况;Rstored(t)为t时段内储能的收益情况;C(t)为t时段内VPP的运行成本;D(t)为t时间段内VPP实际出力与计划出力偏差的惩罚成本。 (3)虚拟电厂t时段内运行成本即C(t)为 C(t)=λstored(Pesd(t)+Pess(t))+λwinPwin(t) (13) 式中,λstored和λwin分别为风电、储能接入VPP的管理系数,通过管理系数对风电、储能进行一定的约束。Pesd(t)和Pess(t)分别为储能的放电和充电功率;Pwin(t)为风电的实际出力情况。 (4)虚拟电厂采用基于价格的需求响应收益即Rload(t)为 Rload(t)=L1(t)P1-L0(t)P0 (14) 式中,L1(t)为t时段内VPP参与需求响应后的负荷使用情况;P1为需求响应后的实时电价;L0(t)为t时段内VPP参与需求响应前的负荷使用情况;P0为需求响应前的实时电价。 (5)虚拟电厂t时段内实际出力与计划出力偏差的惩罚成本即D(t)为 D(t)=αG(t)|ΔPvpp(t)| (15) 式中,α为惩罚系数,VPP实际出力与预测出力偏差越大惩罚系数越大;G(t)为t时间段的惩罚电价;ΔPvpp(t)为t时间段内VPP实际出力与计划出力的偏差值。 (6)虚拟电厂t时段内实际出力与计划出力的偏差值即ΔPvpp(t)为 ΔPvpp(t)=Pwinf(t)+L0(t)-Pwin(t)- (16) 式中,Pwinf为风电的预测出力情况;L0(t)为t时段内VPP参与需求响应前的负荷使用情况;Pwin(t)为风电的实际出力情况;Pesd(t)和Pess(t)分别为储能的放电和充电功率;L1(t)为t时段内VPP参与需求响应后的负荷使用情况。 本文假设VPP由300 MW的风电场,100 MW的储能设备构成,假设储能充放电功率为20 MW,风电、储能设备参数为:风电运行管理系数32.6元/(MW·h),处理范围的上限按照30 MW计算,处理下限按照0计算;储能运行管理系数83元/(MW·h),处理范围的上限按照50 MW计算,处理下限按照0计算[9-10];惩罚电价按照当前电价的2倍进行计算;需求响应前的平均电价按照30元/(MW·h),需求响应后按照峰谷电价可按照不超过25%进行波动[11];VPP中按照风电预测出力误差不大于15%,储能预测出力误差不超过20%[12],并根据VPP预测情况,协调各分布式资源生成最优调度方案。 根据相关资料规定[13],风电的价格按照0.597元/(kW·h)计算,储能可按照不同时段内价格不同计算,如表1所示[14-15]。 表1 储能价格 依据上述数据,对优化结果进行分析。图2给出了风电及储能在某一段时间的出力情况。从图中可以看出,虚拟电厂在风电等新能源设备总出力处于高峰时段可利用分布式储能来储存电量,而在负荷高峰时段来放电,以获取更优的经济效益。进一步对含风电的虚拟电厂和既含有风电又有储能的虚拟电厂进行对比,如图3所以,可以看出含有风电和储能的虚拟电厂比只含有风电的虚拟电厂总利润高,且能提高新能源的消纳比。 图2 风电、储能出力情况 图3 含不同新能源的虚拟电厂总利润对比 当分布式资源参与需求响应后,原负荷曲线与需求侧响应后曲线对比如图4所示,由图4表明,负荷的峰谷差由原来约75 MW变为67.78 MW,且需求侧响应后的负荷曲线相较于原曲线波动更小,具备削峰填谷的作用并根据对分布式资源的预测情况可实时调节虚拟电厂的运行,图5为风电、储能出力预测与实际出力的曲线对比,根据虚拟电厂中分布式风电、储能的误差计算虚拟电厂预测运行与实际运行情况,对VPP经济效益进行分析,如图6所示。 图4 需求响应前后负荷曲线 图5 风电、储能实际出力与预测出力对比 图6 虚拟电厂总收益及出力预测误差情况 表2及图6表明在不同出力预测误差下的VPP收益,结果说明:随着VPP平均误差的减小,惩罚系数随之减小,VPP模型的总经济效益在增加。当平均误差从16.708%降低到6.683 4%时,总收益增加了7.982万元。 表2 不同出力预测误差下虚拟电厂经济性分析 本文提出了一种含有风电、储能及需求响应的虚拟电厂优化调度方法,针对分布式资源的出力的不确定性,协调VPP的各发电单元的工作,弥补不同种类的分布式资源的不足,优化运行。基于风电的预测出力及需求响应策略制定VPP的运行方案,制定日前生产计划安排,并进行日内滚动优化实现分布式资源的实时调控。降低各发电单元的预测出力与实际出力的偏差,使得VPP的运行能按照日前生产计划进行执行,从实验结果可以看出含有多种分布式资源的虚拟电厂比含有单种分布式资源的虚拟电厂发电总利润高,且分布式资源实际出力与预测出力偏差越小,VPP的经济效益越高。2.2 虚拟电厂优化约束条件
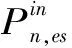
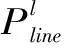
2.3 虚拟电厂最优调度模型

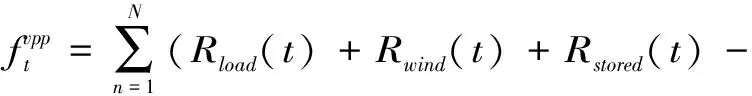
Pesd(t)+pess(t)-L1(t)3 算例分析



4 结 论
