基于多模型融合的中长期径流集成预测方法
2024-02-26朱非林陈嘉乙徐向荣钟平安
朱非林,陈嘉乙,张 咪,徐向荣,钟平安
(河海大学水文水资源学院,江苏 南京 210024)
0 引 言
中长期径流预报在水资源开发调度与管理、水利工程运行与维护以及水旱灾害防御等领域中扮演着重要的技术角色。近年来,随着极端洪涝干旱事件的频发,它也成为水文领域研究应用中备受关注的难点和热点问题。然而,受全球范围内气候和大气环流等复杂要素的综合影响,中长期径流预报缺乏可靠的气象预报信息,导致预报结果的不确定性较大。因此,如何提高预报精度已成为当前研究的重点[1]。
近年来,中长期水文预报研究取得了诸多进展。根据研究方法的不同,预报模型可分为考虑径流时间序列演变特征的序列演变方法和考虑预报因子与径流数量关系的因子关系方法[2]。通过机器学习方法建立预报模型成为当前主流的研究途径,在单一模型预测方面,岳兆新等[3]基于改进深度信念网络模型对雅砻江流域进行中长期径流预测,实现更好的预测速度和精度;杨文发等[4]使用流域多尺度水文预报模型,探讨了流域水文预报中涉及的不确定性因素以及水文气象耦合方面的不匹配性;邵健伟等[5]提出了基于SpringBoot框架的中长期水文预报系统,实现了中长期水文预报业务化运行。在多模型集成预测方面,李宏亮[6]采用加权平均法组合3种不同预报模型实现水文集合预报;周研来等[7]采用Gamma Test数据驱动模型与长短期记忆神经网络结合3种机器学习算法的综合模型,以解决在变化环境下降雨-洪水过程统计的非线性、随机性和时变性问题;Tan等[8]采用EEMD-ANN混合方法建立适合长江流域汛期月径流的预测模型;Liu等[9]将隐马尔可夫模型与高斯混合回归相结合,证明其可以处理多模态和异方差数据。然而,单一预报模型虽然可以通过特征提取、参数优化等方式提高预测精度并缩短训练时间,但其模型结构相对固定,参数选择范围有限,考虑因子无法适应不同流域。现有集成预测方法大多研究多个确定性模型的加权组合,但由于不同模型数据结构、参数形式和变量分布具有复杂性,简单的随机加权容易导致过拟合现象。
鉴于此,本文提出了一种基于多模型融合的水库中长期径流集成预测方法。采用Stacking融合算法,选取ARMA、BP、LSTM、RF和SVR等5个异质预测模型进行融合,并通过超参数寻优方法对这些模型进行参数优化。以黄河上游龙羊峡水库作为研究对象,验证了该方法在提高中长期径流预报精度方面的有效性。
1 研究方法
图1为基于多模型融合的中长期径流集成预测框架流程图。首先,采用相关性分析确定与径流显著相关的因子,并利用主成分分析降低数据维度,完成预报因子的筛选。然后,使用不同累积贡献率的主成分组对应的基学习器进行训练,并采用超参数优化寻优,得到各基学习器的最优主成分结果。最后,通过K折交叉验证处理最优主成分结果,训练元学习器预测模型,得到多模型融合的预测结果。
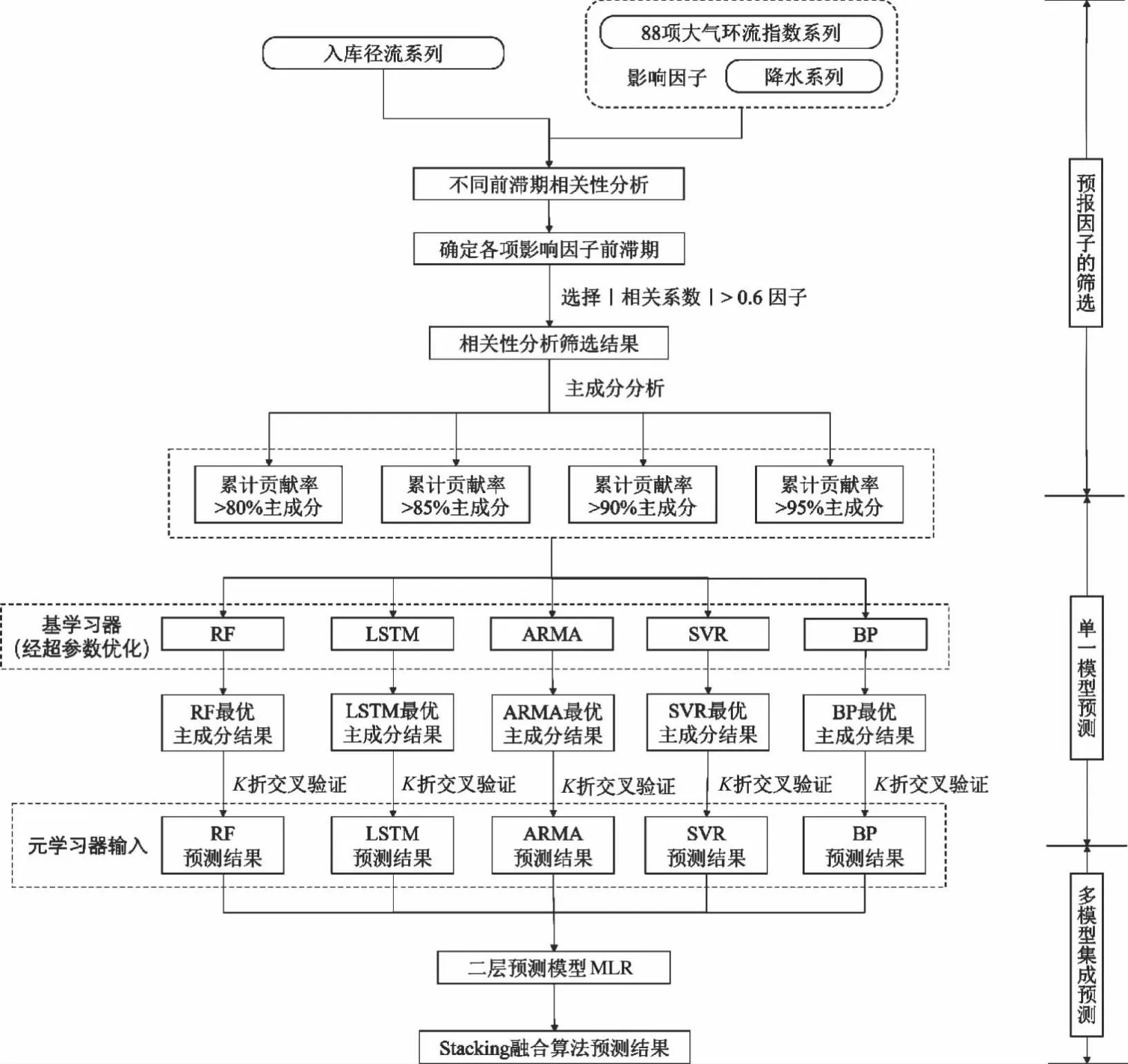
图1 基于多模型融合的中长期径流集成预测框架
1.1 预报因子的筛选
1.1.1 初始预报因子集
中长期径流变化的复杂性使其影响因子的类型较多。本文从影响中长期径流变化的机制出发,选择前期径流变量、大气环流因子、水文要素因子3类因子作为研究数据。具体包括:1959年~2016年龙羊峡水库逐月入库径流量;1959年~2016年中国气象局国家气候中心88项大气环流指数逐月数据;1959年~2016年青海省西宁气象站逐月降水数据。
1.1.2 相关性分析
相关性分析是一种常用的统计分析方法,用于研究两个或多个变量之间的相关性或关联性,甄别对径流变化贡献大、作用强的影响因子。本文采用Spearman相关系数来衡量径流量与影响因子之间的相关程度,其公式为
(1)

1.1.3 主成分分析
主成分分析(PCA)是一种常用的多元统计分析方法,该方法通过对一组变量的线性组合来寻找变量间的主要模式和结构,将多个变量转化为少数几个主成分,在降低维度的同时使保留的信息量最大化。
假设原始样本为X={x1,x2,…,xm},xi∈Rn,样本数m个,每个样本有n个特征维度。对样本进行标准化变换,得标准化矩阵Z。
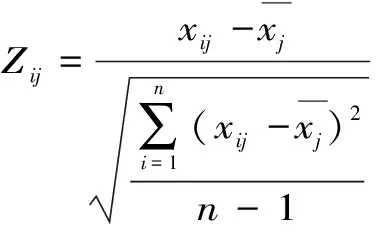
(2)
对标准化矩阵Z求相关系数矩阵,rij为两变量之间的相关系数,相关系数矩阵R为
R=[rij]n
(3)
解样本相关系数矩阵R的特征方程|R-λIn|=0,λ为特征根,In为特征向量,按不同方差贡献率a确定各因子的信息利用率,即
(4)

(5)
1.2 单一预测模型
本文选择在水文预报领域经过大量实践验证的5种具有典型性、代表性、异质性的单一模型,分别是属于监督学习类的支持向量回归模型(Support vector regression,SVR)、BP神经网络模型(BP neural network,BP);属于集成学习类的随机森林模型(Random forest,RF);属于时间序列分析类的自回归滑动平均模型(Autoregressive moving average model,ARMA);属于深度学习类的长短期记忆神经网络模型(Long short-term memory,LSTM)。
1.2.1 自回归滑动平均模型
ARMA模型是一种基于时间序列分析的预测模型,结合了自回归(AR)和移动平均(MA)模型,可被用于描述时间序列中的自相关和移动平均关系。
AR模型yt=c+∑(φiyt-i)+εt
(6)
MA模型yt=μ+εt+∑(θtεt-i)
(7)
ARMA模型
yt=c+∑(φiyt-i)+εt+∑(θtεt-i)
(8)
式中,yt为时间序列的观测值;c为常数项;φi和θt分别为AR和MA模型的系数;εt为误差项;μ为时间序列的均值。
1.2.2 BP神经网络模型
BP预测模型是一种基于人工神经网络的机器学习算法,用于解决回归和分类问题。它通过反向传播算法来训练神经网络,不断调整权重和偏置使预测值与实际值之间的误差最小化。模型结构如图2所示。

图2 BP神经网络模型结构
1.2.3 长短期记忆神经网络模型
长短期记忆网络LSTM是循环神经网络(RNN)的一种改进算法。LSTM的细胞单元包括输入门、遗忘门、输出门,其中输入门用于控制信息输入,遗忘门用于控制是否遗忘历史序列信息,输出门用于控制信息输出。
遗忘门中输入xt与状态记忆单元St-1、中间输出ht-1共同决定状态记忆单元遗忘部分。输入门中的xt分别经过sigmoid和tanh函数变化后共同决定状态记忆单元中保留向量。中间输出ht由更新后的St与输出ot共同决定,计算公式为
ft=σ(Wfxxt+Wfhht-1+bf)
(9)
it=σ(Wixxt+Wihht-1+bi)
(10)
gt=σ(Wgxxt+Wghht-1+bg)
(11)
ot=σ(Woxxt+Wohht-1+bo)
(12)
St=gt⊙it+St-1⊙ft
(13)
ht=φ(St)⊙ot
(14)
式中,ft、it、gt、ot、ht和St分别为遗忘门、输入门、输入节点、输出门、中间输出和细胞单元的状态;Wfx、Wfh、Wix、Wih、Wgx、Wgh、Wox、Woh分别为相应门与输入xt和中间输出ht-1相乘的矩阵权重;bf、bi、bg、bo分别为相应门的偏置项;⊙为向量中元素按位相乘;σ为sigmoid函数变化;φ为tanh函数变化。
1.2.4 随机森林模型
随机森林是一种基于Bagging思想和特征子空间思想的集成学习模型,以多个由Bagging技术训练得到的决策树作为基学习器,组合单个决策树的输出结果,投票决定最终分类结果。随机森林模型具有较强的非线性模拟能力,不易出现过拟合现象,对数据集特征的挖掘的鲁棒性强[10]。
通过K轮训练,以Bagging抽样技术从原始训练集{(xi,yi),xi∈X,yi∈Y,i=1,2,…,N}中产生K个决策树{h(X,θk),k=1,2,…,K},其中N为样本容量,θk为由Bagging思想和特征子空间思想产生的随机变量序列。用它们构成集成学习模型,以投票法产生最终分类决策,即
(15)
式中,H(x)为组合分类模型;h(X,θi)为单个决策树模型;Y为目标变量;I为示性函数。
1.2.5 支持向量回归模型
支持向量回归(SVR)是一种用于预测连续数值型目标变量的机器学习模型。它基于支持向量机(SVM)的原理,在高维特征空间中找到一个超平面,最小化预测值与实际值之间的误差。SVR目标函数(误差最小化)为
(16)
式中,ω为超平面的权重向量;x为输入特征向量;y为实际值;f(x)为预测值;ε为控制模型容忍误差的参数;C为正则化参数。
1.3 超参数优化
超参数的选择与估计是机器学习模型在实际应用中的关键问题,模型泛化性能的优劣依赖于对超参数的合理选择[11]。超参数优化是一种通过寻找最优超参数值来优化模型性能的方法,目标是在超参数空间中找到使目标函数最小化或最大化的超参数组合。
常见的超参数优化方法有网格搜索、随机搜索、贝叶斯优化等。其中,随机搜索要求样本点集足够大,贝叶斯优化算法容易陷入局部最优值。而网格搜索在采用较大的搜索范围及较小的补偿时,有更高概率获得全局最优值[12]。本文主要采用GridSearchCV方法进行超参数寻优。该方法是一种基于网格搜索的交叉验证方法,将超参数空间划分为多个网格,然后对于每个网格对应的超参数组合进行模型训练和评估,选择最优结果[13]。
1.4 多模型集成预测
1.4.1K折交叉验证
K折交叉验证方法是一种用于提高分类效果的统计分析方法。将样本量大小为N的数据集划分为大小近乎相同但互不交叉的K份数据集,并以不同方式组合为训练集与测试集。“交叉”意为某种组合方式中训练集的样本,在另一组合方式中可能成为测试集,重复使用数据。其中训练集用于训练模型,测试集用于评估模型性能。该方法可使两层使用的训练数据不同,在一定程度上防止过拟合。
1.4.2 Stacking融合算法
Stacking融合算法被广泛应用于多种学习器的组合。该算法分为2层,先训练第一层中的多个基学习器,产生的结果作为输入训练第二层中的元学习器,得到最终输出。基学习器的选择对算法的预测精度有重要影响,学习能力较强的基学习器可提升算法的预测精度;同时,基学习器间的异质性可弥补不同基学习器的短板,进一步提升模型的泛化能力。元学习器的训练集由基学习器的输出产生,直接使用基学习器来产生元学习器时,容易造成过拟合。选择较简单的元学习器可有效降低过拟合风险。本文采用多元线性回归(MLR)模型对5种单一模型预测结果进行拟合,MLR模型是多元回归分析中最基础,最简单的模型,适合作为Stacking融合算法中的第二层学习器。算法原理如图3所示。

图3 Stacking融合算法原理示意
本文采用的Stacking融合算法中,第一层为K折交叉验证方法下的5种单一模型预测结果,将输入数据训练集划分为5折对每个单一模型进行交叉验证,验证后组合的训练集作为单一模型的输入项,得到5组预测结果。第二层将5组预测结果输入多元线性回归模型,分析每组输入项的权重分配,得到最终预测结果并与单一模型结果进行比较。算法结构如图4所示。

图4 双层Stacking融合算法结构示意
1.5 模型评价指标
本文选取4种常用评价指标来衡量模型预测精度,分别为平均绝对误差(Mean absolute error,MAE)、均方误差(Mean square error,MSE)、平均绝对百分比误差(Mean absolute percentage error,MAPE)和确定性系数(R-square,R2)。各项指标计算公式如下
(17)
(18)
(19)
(20)
式中,MAE、MSE、MAPE指标值越小,R2指标越接近1,说明模型拟合效果好,预测结果误差小;反之,模型拟合效果差,预测结果误差大。
2 实例分析
2.1 研究区域概况
龙羊峡位于青海省共和县与贵南县交界处的黄河上游干流河段,龙羊峡水电站是黄河上游第一座大型梯级电站,水库控制流域面积13.1万km2,调节库容193.6亿m3,总库容247亿m3。库区海拔高程2 600~3 000 m,多年平均流量650 m3/s。
2.2 因子相关性分析
为分析各项大气环流指数与龙羊峡水库月入库径流在时间尺度上的变化,确定预报因子的前滞期,将龙羊峡水库月入库径流与前1~4个月的88项大气环流指数进行相关性分析,结果如图5所示。龙羊峡水库月入库径流与前1个月的大气环流指数相关性最大,前滞期为2个月、3个月时,相关性明显随滞时增加而减小,前滞期为4个月时部分环流指标相关性由正相关变为负相关,但大多数相关系数绝对值仍明显小于前滞期为1个月时对应的相关系数。故选取大气环流指数影响因子前滞期为1个月。

图5 不同前滞期龙羊峡月平均径流与大气环流指标相关性比较
利用相关性分析确定水文要素因子的最佳前滞期,选取前滞期分别为1~4个月,对不同前滞期龙羊峡水库月入库径流量与不同前滞期西宁站月降水量作相关性分析,如表1所示。由表1可知,龙羊峡月径流量与西宁站降水量在前滞期为1个月时相关性最大,随着前滞期增长,相关系数逐步减小,前滞期4个月时由正相关转为负相关,但相关系数绝对值仍小于前滞期1个月时的相关系数。故选取水文影响因子的前滞期为1个月。将各项影响因子的月数据前滞1个月,与龙羊峡水库当月入库径流量做相关性分析,选择相关系数大于0.6的影响因子作为筛选结果。
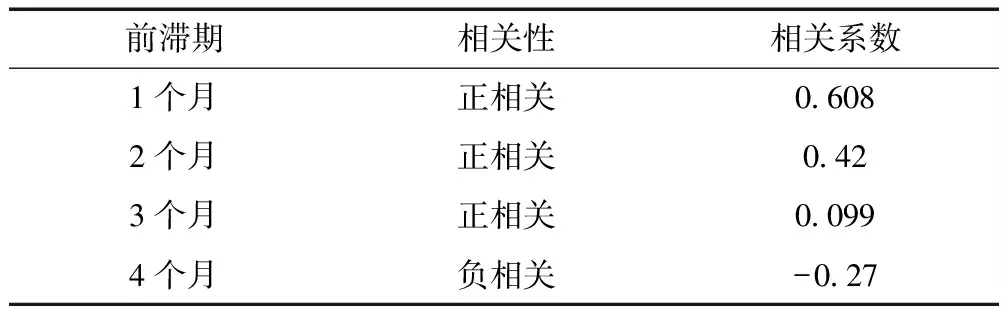
表1 不同前滞期龙羊峡月平均径流与西宁站降水量相关性比较
2.3 因子综合筛选
对使用相关性分析筛选出的36项影响因子进行主成分分析,结果如表2所示。以不同的累计贡献率为界限来确定输入项:以80%的累计贡献率为下限,提取主成分4个(CA1~CA4),累计贡献率达81.85%;以85%的累计贡献率为下限,提取主成分6个(CA1~CA6),累计贡献率达87.10% ;以90%的累计贡献率为下限,提取主成分8个(CA1~CA8),累计贡献率达90.46%;以95%的累计贡献率为下限,提取主成分13个(CA1~CA13),累计贡献率达95.79%。根据主成分的荷载计算分别得到4组主成分序列(CA4、CA6、CA8、CA13)作为中长期径流预报模型的输入因子。
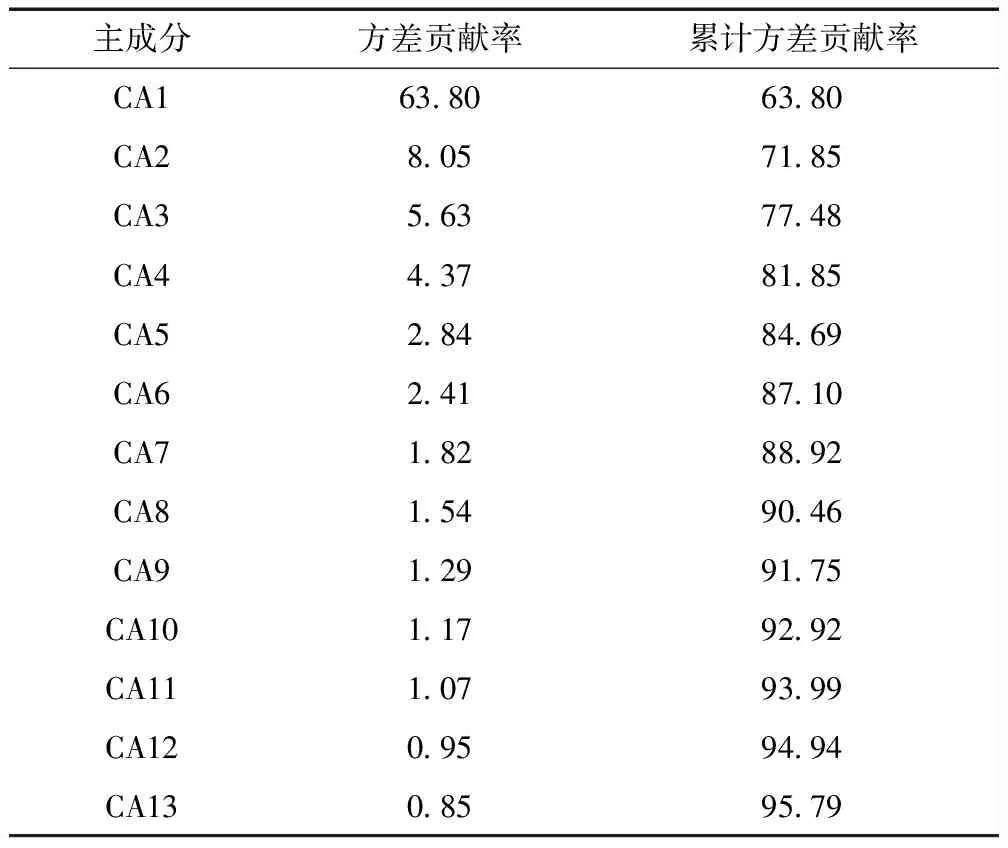
表2 因子综合筛选结果 %
2.4 单一模型预测结果
以默认参数建立5个单一模型,划分输入因子前495项为训练集,后200项为测试集,使用GridsearchCV方法进行超参数寻优,得到最优参数下的不同主成分组合的预测结果,对其精度指标进行比较,以最优主成分组合得到的结果作为单一模型的最优预测结果。每个模型的预测结果对比如图6所示,精度指标如表3所示。
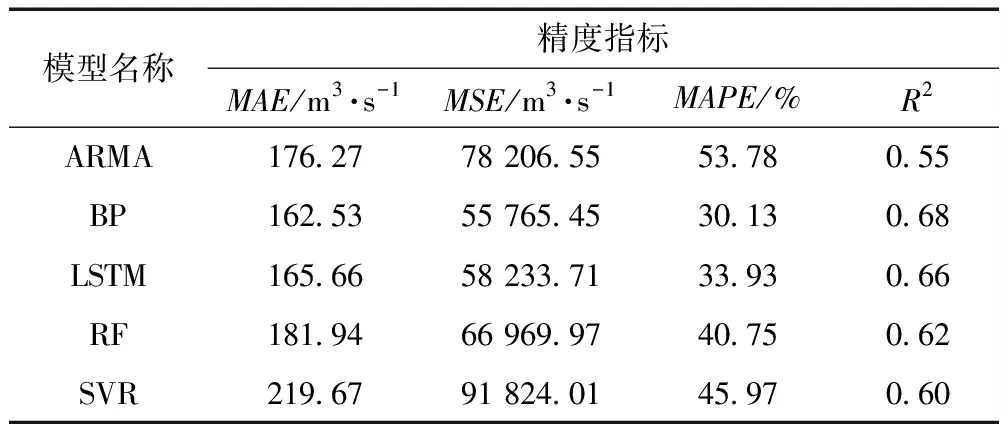
表3 单一模型预测精度指标(K折交叉验证前)

图6 单一模型预测值与实测值对比
超参数优化前后预测结果对比(以MAPE指标为例)如表4所示。

表4 超参数优化前后单一模型预测结果精度对比 %
由表3和表4可知,不同的单一模型对龙羊峡径流预报效果具有一定的差异性;超参数寻优方法对模型精度有一定提升,但是仅局限于模型参数的优化,模型本身存在的缺点导致的精度误差无法避免,预测结果有待进一步优化。
2.5 多模型集成预测
第一层Stacking将5个单一模型分别采用5折交叉验证进行预测,输入因子使用最优主成分组合,模型参数采用超参数优化后的最优参数,预测结果对比如图7所示,精度指标如表5所示。

表5 单一模型预测精度指标(K折交叉验证后)

图7 K折交叉验证后单一模型预测结果与实际值的对比
对比表4和表5可知,K折交叉验证后MAE、MSE、MAPE指标值减小,R2指标提高,说明K折交叉验证后一定程度上降低了过拟合,有效提高了预测精度。
第二层Stacking以单一模型的预测结果作为MLR模型的输入因子,通过超参数寻优得到单一模型的最优权重,得到最终预测结果对比,如图8所示,精度指标与单一模型K折交叉验证后对比如表6所示。
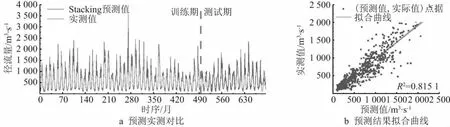
图8 Stacking融合算法预测结果与实际值的对比
由表6可知,基于多模型融合的集成预测方法的MAE、MSE、MAPE指标值最小,R2指标最接近1,说明模型拟合效果好,预测结果误差小,预测效果相较于单模型有较大的精度提升。
3 结 论
本文提出了一种基于多模型融合的集成预测方法,通过结合5个异质模型,建立了龙羊峡水库中长期径流预测模型。同时,采用超参数寻优方法对各模型参数进行了优化,将得到的预测结果与单一模型的预测结果进行比较,得出以下结论:
(1)采用超参数优化方法确定模型的最优参数,可以有效提高融合后的集成模型的预测精度。
(2)本文使用了Stacking融合算法,并采用了K折交叉验证策略,有效避免了模型训练中出现的过拟合现象,进一步提升了预测精度。
(3)基于Stacking融合算法,将ARMA、BP、LSTM、RF和SVR等5个异质模型进行了融合。与单一模型相比,集成预测方法取得了更高的精度,R2值从0.71提升至0.82。
