混合Beta分布GARCH模型的EM算法求解与实证分析

石 凯，刘洪江，孙 峰

（乐山师范学院a.数理学院；b.旅游学院，四川 乐山 614000）

0 引言

时间序列分析是考察经验样本数据随时间演变的学科，由于时序样本的走势与波动都包含着不确定的随机因素，因此统计的理论和方法在其中起着重要作用。单变量时序数据信息的提炼主要集中在均值的平稳性和波动的方差齐性两个方面。关于时序均值平稳性信息的提炼可以依据差分整合自回归移动平均（ARIMA）模型，但是ARIMA模型设定的前提条件要求方差齐性。如果时序数据资料中存在违背方差齐性的特征，则还需要进一步提取异方差信息。异方差所呈现的类型也有很多，在金融市场领域中广泛具有的是一种条件异方差特性，即在波动偏大的时段持续偏大，波动偏小的时段持续偏小，也称为集群效应。集群效应处理对应的方法是自回归条件异方差（ARCH）模型，最初是由Engle（1982）[1]在分析英国通货膨胀率序列时提出的对残差平方进行的一种自回归建模方法。在实际应用中，ARCH模型拟合异方差函数往往会产生较高的移动平均阶数，为克服这一缺陷，Bollerslev（1986）[2]提出广义自回归条件异方差，即GARCH 模型。GARCH模型的提出，有效解决了异方差的长记忆性问题，成为现今普遍采用的处理时序数据条件异方差的方法。

为了拓展GARCH 模型的应用范围，提升时序波动特征的拟合和预测精度，学者们从不同角度出发，在GARCH模型的基础上衍生出一系列模型。然而，需要指出的是，经典GARCH族类模型中均对模型作了正态分布的假定，可是在处理一些特殊领域，尤其是金融市场时，这一假定存在严重的问题。Hsieh（1989）[3]在对金融市场汇率的相关研究中指出，可以用GARCH（1,1）模型解释汇率波动的绝大部分信息，但是正态分布设定却不能捕获金融数据特有的“高峰厚尾”特征（即在均值附近的样本点比正态分布多，取极端值的样本点也比正态分布多）。此后，关于金融市场的一些特殊特征一直是学术界研究的热点之一，如Clark 和Baccar（2018）[4]在研究信用利差波动率的变化情况时证实，利差数据除了高峰厚尾外，还具有非对称性等特征，与传统GARCH模型的正态性假定严重不符。同样，国内金融市场也不例外，徐龙炳（2001）[5]、别晓芳（2018）[6]等均指出中国金融市场也不服从正态分布的特性；同时，白仲林等（2011）[7]还认为受我国当前经济发展水平和金融制度的限制，金融市场的资产收益率等序列还具有“有界取值区间”的特征。

针对此类特性的刻画，众多文献指出要采用非正态分布来弥补模型设定的缺陷[8—10]。这些文献扩展了模型的应用范围，重点提取了金融市场的高峰厚尾、非对称性等信息，但是由于金融市场，尤其是国内金融市场的一些特殊制度和交易规则，使得时序数据的波动存在有界的取值区间。而正态分布、t 分布、GED 分布、混合高斯分布等分布类型的变量取值范围都是整个实数域，严重制约了GARCH 族模型在现实环境中的应用。因此，为进一步拓展GARCH模型的应用领域，本文试着引入变量取值为有界区间（0,1）的Beta分布，并构建混合Beta分布的GARCH模型，以期能有效提取金融市场波动的复杂特性。同时，为考察混合Beta 分布对GARCH模型刻画能力的改进，本文给出了模型设立原理与求解过程，并通过模拟仿真数据和现实金融数据，对参数估计效果进行了比较和检验。

1 混合Beta分布GARCH模型的构建

1.1 GARCH模型的一般形式

GARCH 族模型是一种自回归条件异方差模型，实质是将历史波动信息作为条件，并采用自回归形式来刻画波动的演变规律，基本GARCH模型的设定形式如下：

其中，yt是可观测的时序数列。式（1）是均值方程，用以刻画均值的信息；式（2）是对式（1）残差项的异方差进行处理，使其转化为一个白噪声序列；波动信息的提炼主要体现在式（3）上，也是GARCH模型的核心，使用自回归的方式提取时序数列波动中蕴含的自相关信息。经典GARCH 模型中假定白噪声序列et是服从均值为0、方差为1的正态分布，即(0, 1)。则由GARCH模型的结构可以得出εt|(εt-1,εt-2,…;ht-1,ht-2,…)~N(0,ht)，以及可观测序列yt的条件分布为N(w,ht)。由此可见，经典GARCH 模型正态分布的假定限制性太强，若序列存在高峰厚尾、非对称、波动有界等特征，则难以进行有效的信息获取，为此，需要放宽模型分布的设定假设，以便得出更符合现实需求的研究结果。

1.2 混合Beta分布及其性质

在概率统计中，Beta 分布是一类定义在有界区间(0,1)上的连续型概率分布，若随机变量X服从Beta 分布，用f(∙)表示Beta 分布的概率密度函数，则其对应的概率密度函数形式为：

式（2）中，Γ(∙)为Gamma函数，α和β为参数，且要求满足α>0，β>0。Beta分布对应的期望与方差分别为：

相比而言，其他分布往往形态单一，而Beta 分布的形态更具有灵活性，随着参数α、β不同而不同。当α、β>0 时为单峰型形态；当α=β时为对称型分布；当α≠β时为非对称型分布，随α、β取值的增大，峰度增加；当0<α、β<1 时呈现“U”型形态；当(α-1)(β-1)≤0 时呈现“J”型形态，即在0 或1 边界的取值范围对应的概率增大。有学者指出，利用多个Beta 分布的混合加权，能够对金融市场特有的高峰厚尾、非对称、有界取值区域等特征进行测度。因此，假设随机变量X由K个Beta分布加权混合构成，记ωk为第k个Beta 分布的权重，k=1,2,…,K，h(∙)为混合Beta 分布的概率密度函数，则X的概率密度函数为：

式（5）中，为保证f(x)作为概率密度函数所须满足的非负性和规范性等基本性质，要求ωk≥0，且若记混合Beta分布的均值为m，方差为d2，组合中的第k个Beta分布的均值为μk，方差为σ2k，则：

1.3 混合Beta分布的GARCH模型构建

将混合Beta 分布引入GARCH 模型中，令式（2）中，其中X的分布由式（5）的形式决定，即将式（2）中的et设定为服从均值为0、方差为1 的非标准混合Beta分布。同时，根据GARCH模型的结构，εt服从均值为0、方差为ht的非标准混合Beta 分布；可观测序列yt服从均值为w、方差为ht的非标准混合Beta分布，即有：

其中，d>0，ht>0。式（8）说明可观测序列yt是随机变量X（服从混合Beta 分布）的单调递增线性变换函数，记yt的概率密度函数为g(yt)，根据概率论知识可得yt的概率密度函数为：

由此，在得到观测值序列yt,t=1,2,…,T后，可以建立GARCH 模型的似然函数。对于金融市场而言，GARCH（1,1）模型能解释波动的绝大部分信息，所以本文选择GARCH（1,1）模型进行分析。对式（3）选择滞后阶数p与q均等于1，得到对应GARCH（1,1）模型的对数似然函数为：

其中，待估参数Λ=(w,γ0,η,λ,ωk,αk,βk;k=1,2,…,K)。

2 模型估计的EM算法求解

EM算法最初由Dempster等（1977）[11]提出，当似然函数有多余参数或含有隐变量时，可以通过两步迭代进行求解，先进行E步，求均值以去掉多余参数，再进行M步，求似然函数的极大值，反复迭代E步和M步，直至收敛。而要采用EM算法，就要先构建包含隐变量的完全数据的似然函数。

2.1 完全数据的似然函数构建

假设时序样本{yt,t=1,2,…,T}是从式（9）的非标准混合Beta分布中产生的，能观测到的是样本序列的取值yt，但是混合权重{ωk,k=1,2,…,K}是无法观测的，所以对混合分布数据来说含有缺失的隐变量，也称为不完全数据或者缺失数据。假设式（9）的生成是先以概率ωk抽取到第k个分量，然后再以这个分量的概率分布密度抽取到yt，其中该分量的概率密度函数为非标准的Beta分布，即有：

其中，fk(∙ |αk,βk)为式（4）Beta分布的概率密度函数，m和d分别由式（6）和式（7）决定。由此可以引入一个不能观测的随机隐变量{zt,t=1,2,…,T} ，zt取值为1,2,…,K，当zt=k时，说明第k类分量被抽中，对应概率即为P(zt=k)=ωk，显然满足：

可见，缺失数据yt对应的完全数据样本序列应为{(y1,z1),(y2,z2),…,(yT,zT)}，对应概率密度函数为g(yt,zt)，虽然统计推断只能基于缺失数据g(yt)进行，但是可以通过全概率公式建立两者之间的关系：

所以，基于观测数据{yt,t=1,2,…,T}的对数似然函数可改写为如下形式：

其中，θ=(w,γ0,η,λ,αk,βk;k=1,2,…,K)，而包含隐变量的完全数据对应的对数似然为：

针对式（12）基于完全数据对数似然函数的最大化就可以用EM 算法求解，结合混合Beta 分布GARCH 模型的对数似然函数式（10），可以给出EM 算法的具体求解过程。

2.2 E步（求期望）

E 步，英文Expectation 的简写，即求期望。EM 算法也是一种迭代算法，以上标“*”标记上一步迭代值，记上一步参数θ的估计值为θ*，则在给定yt和θ*时，E步是计算完全数据对数似然函数关于未观测数据zt的条件期望，该条件期望也称为Q函数[12]。

其中，f(∙)为Beta 分布的概率密度函数，将上式进一步分解可得由两个部分构成的Q函数：

2.3 M步（最大化条件期望）

M 步，英文Maximum 的简写，表示最大化条件期望Q(θ|θ*)函数。根据式（13），前一部分仅与ωk有关，后一部分与参数向量θ=(w,γ0,η,λ,αk,βk;k=1,2,…,K)，即不包含ωk的部分有关，同时注意到，所以关于ωk有约束的一阶条件为：

其中，τ为拉格朗日乘子，求解可得：

其中，ω*k为参数ωk的上一步迭代值，gk(yt|θk*)由式（11）决定。

对于其余参数(w,γ0,η,λ,αk,βk;k=1,2,…,K) 的估计只需最大化式（10）的后一部分。令：

其中：

可见，与参数(w,γ0,η,λ,αk,βk;k=1,2,…,K)有关的部分在于ln(∙)部分，该H函数求解时无法得到显式表达式，可以通过数值解方式求其极大值。最后，不断重复E步和M步，直至收敛。EM算法在计算机上实现较为容易，其优点是每次迭代都增加似然函数的数值，一直到逼近最大值，因此尤其适合混合概率分布模型的参数估计求解。

2.4 EM算法实施流程

基于EM算法的混合Beta分布GARCH模型参数估计的流程可归纳如下：

（1）选取参数(w,γ0,η,λ,ωk,αk,βk;k=1,2,…,K)的初始值。

（2）依据当前模型参数值，生成混合Beta分布GARCH模型的ht序列。

（3）E步：代入参数当前值和序列ht，计算Q函数。

（4）M 步：最大化Q 函数，计算下一轮的参数迭代值(w,γ0,η,λ,ωk,αk,βk;k=1,2,…,K)。

（5）重复步骤（2）至步骤（4），直至收敛。

3 基于仿真模拟数据和现实数据的实证分析

3.1 仿真模拟数据的生成过程

假定一条GARCH（1,1）时间序列链生成过程为：

其中，et设置为由两个Beta分布混合而成，具体形式为：0.85 ∙Beta(38,38.5)+0.15 ∙Beta(3.5,3.6)，即混合权重为0.85和0.15。采用模特卡洛仿真的方式，在计算机上模拟生成一条T=1000的序列yt，并将yt序列的走势图及其分布直方图分别绘制为图1 和图2。从图1 可以看出，yt序列的走势符合GARCH模型特征，即自回归条件异方差特征，当前序列的波动受到往期波动的影响；进一步对yt和进行Box检验，选择滞后期为12期，yt序列的Q统计量对应的P 值为0.86，认为yt序列不存在自相关特征，但是序列的Q统计量对应的P值为2.2×10-16，显著拒绝不存在序列自相关的原假设，所以Box检验结果也验证了yt序列符合GARCH模型的生成机理。从图2的yt序列分布直方图来看，序列分布具有明显的高峰厚尾、有限取值区域等特征，图形中附加的分布曲线是以yt的均值和方差绘制的正态分布的概率密度曲线，对比可知正态分布的设定难以有效刻画数据的真实特征，若不进行分布类型假设的调整，则势必会产生模型设定上的偏误问题。

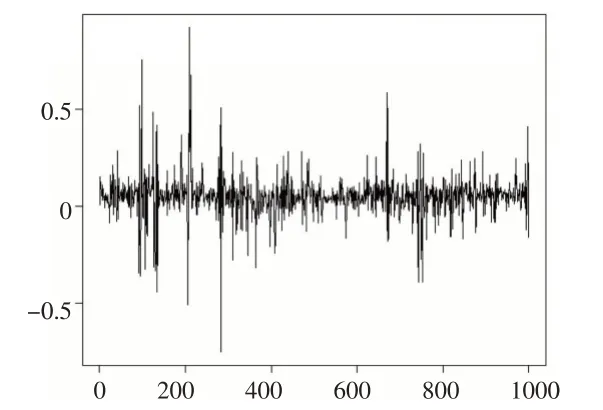
图1 yt 序列走势图

图2 yt分布直方图

3.2 模型参数的求解

根据前文给出的混合Beta分布GARCH模型的EM算法流程对yt序列进行参数估计求解，待估的参数向量包括(w,γ0,η,λ,ω1,ω2,α1,β1,α2,β2) ，对应的真值分别为（0.05, 0.0015, 0.4, 0.5, 0.85, 0.15, 38, 38.5, 3.5, 3.6），对于GARCH 模型的现实应用来说，尤其关注系数η和λ的估计，反映当前序列波动受到往期波动影响的程度。同时，为了对比不同分布类型假定下，参数求解的效果，本文将正态分布假定和混合Beta 分布假定进行了对比。传统的GARCH 模型假定(0,1) ，根据模型结构可知(w,ht)，由此可得出样本对数似然函数式（16），从而进行MLE求解，待估参数仅包括(w,γ0,η,λ)。

对yt序列建立GARCH(1,1)模型，基于正态分布假设的参数估计和基于混合Beta 分布的参数估计的结果如表1所示。

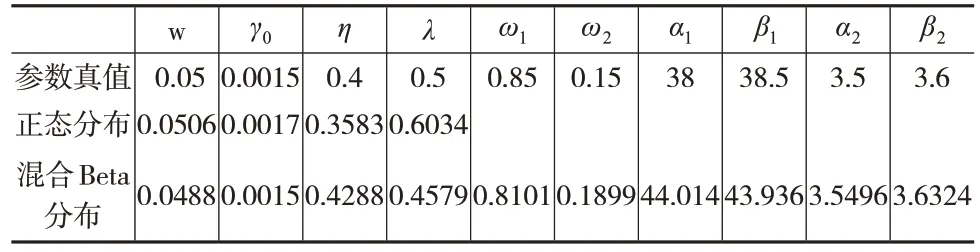
表1 yt 序列各参数估计结果

从表1的结果可知，混合Beta分布的参数估计与参数真实值的结果更为接近；同时，就本例而言，基于正态分布假设倾向于高估前一期条件方差的影响，低估GARCH项的影响程度，而基于混合Beta 分布正好相反。事实上，在金融市场里面，波动信息的冲击往往具有较为持久的效应，因此采用混合Beta分布的模型设定在此类领域中更具有重要的现实意义。

3.3 现实数据分析

为了进一步体现模型的现实应用意义，本文选取从2015 年1 月1 日至2022 年6 月24 日1818 个交易日上证指数的收益率数据进行实证研究，去除掉序列自相关后的收益率序列标记为rt。序列走势图和其分布直方图分别见图3 和图4。从图3 的rt序列走势图来看，序列的波动具有GARCH模型的集群效应。从图4的rt序列分布直方图来看，序列分布的高峰厚尾、有限取值区域、非对称等特征明显，图4中附加的分布曲线是以rt的均值和方差绘制的正态分布的概率密度曲线，对比可知正态分布的设定难以有效刻画金融市场数据的真实特征。因此，本文运用混合Beta 分布GARCH 模型进行信息的提炼，考虑到计算量的大小，采用两个Beta 分布的混合形式。同时，由于收益率序列rt受我国股票市场涨跌停板的限制，取值区间为[- 0.1,0.1] 的有限区域，因此通过线性变换(rt+0.1)/0.2 将rt的取值范围转换到Beta 分布的区间[0 ,1] 上。表2 展示了EM算法的参数求解结果。为了对比，也给出正态分布设定下的估计结果。从表2的结果来看，在正态分布假定下，对GARCH项影响的估计结果偏高，而对前一期扰动项平方影响的估计结果偏低；而在混合Beta 分布设定下，对这两项的估计结果进行了修正，加强了前一期扰动项平方的影响，减弱了GARCH项的影响。虽然在金融市场中波动信息的冲击具有较为持久的效应，但是相对而言，近期随机信息冲击对当前条件方差的影响较大，较远时期的影响会随着时间间隔的增加逐渐减弱。因此，混合Beta分布GARCH模型的估计结果更为合理。

表2 rt 序列各参数估计结果

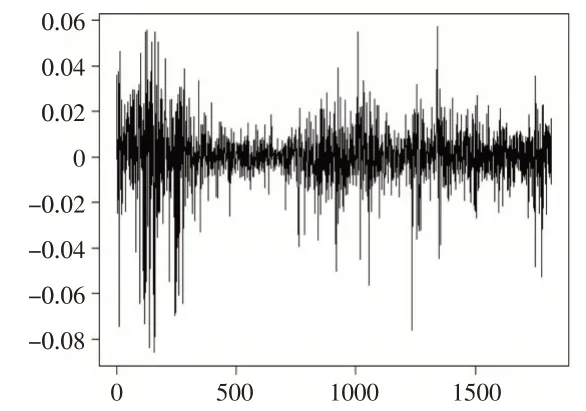
图3 rt 序列走势图

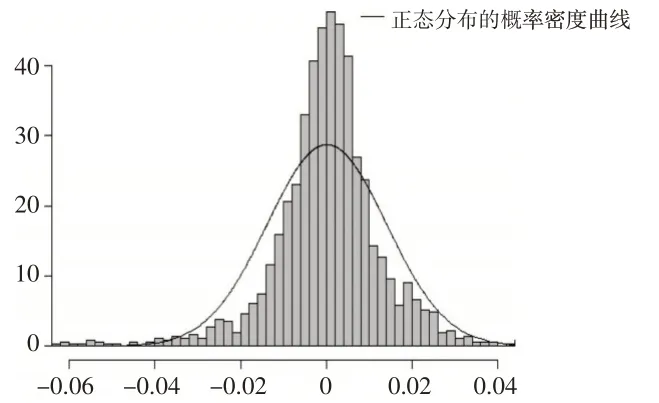
图4 rt 分布直方图

4 结束语

经典GARCH模型可以用来解决时序数据资料分析中方差齐性设定所引起的问题，通过将方差的条件自相关特性引入模型中，从而能更准确地拟合时序变量波动的变化规律。然而，在金融市场等现实领域中，还需关注的一个重要问题是模型分布类型的设定，高峰厚尾、非对称、取值区间有限等特征难以被单一的正态分布所刻画。有鉴于此，本文提出了基于混合Beta 分布的GARCH 模型，并通过分析给出了模型参数求解的EM 算法流程。基于模拟数据和现实数据的实证分析结果均显示，混合Beta分布能更有效提炼波动的非正态性信息，同时，也验证了EM 算法对模型的参数求解行之有效。需要指出的是，EM 算法也存在缺点，如对初始值的设置敏感、得到的最优解是局部最优、收敛速度较慢等，而且至今还没有较好的解决方案。因此，在未来的进一步研究中，关于EM 算法的优化是一项值得探讨的课题。