基于混合需求的高铁快巴动态线路规划方法研究

王瑜琼

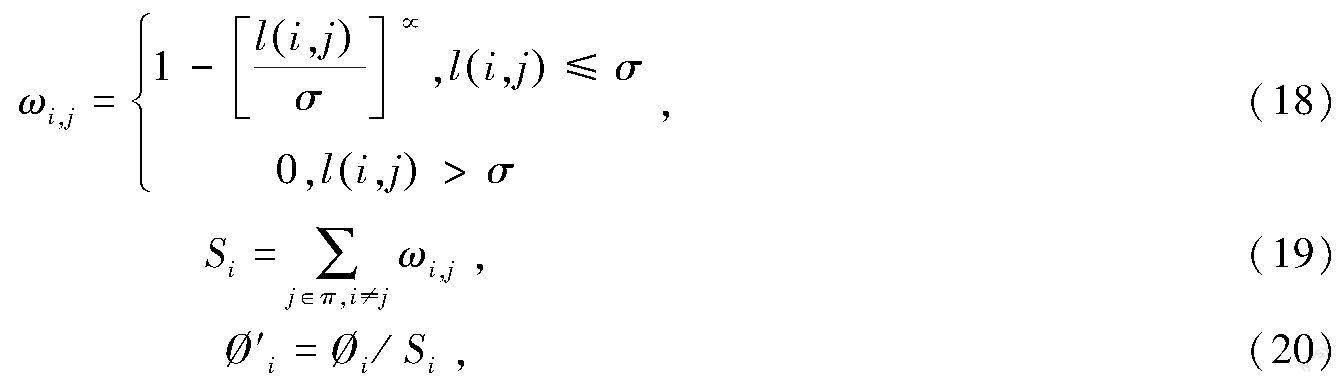
摘要：为满足旅客在高铁站的接驳及疏散需求，增强高铁站作为城市综合交通枢纽的作用，建立基于提前预约和实时混合需求的高铁快巴动态线路规划模型。在运营开始前，基于提前预约需求，兼顾公交公司的运营成本和乘客出行时间成本，建立线路规划模型；利用小生境技术对传统遗传算法进行改进，设计算法求解。运营开始后，允许实时需求插入既定路线，引入临时站点，以最小化系统变动成本为目标，建立整数规划模型决策动态线路规划方案。应用本方法在北京市北太平庄街道区域随机生成并求解30组需求算例。结果显示，该模型可以在两阶段生成最优的高铁快巴线路方案满足混合需求；与传统遗传算法相比，小生境遗传算法有效避免了算法早熟，运算结果更优，模型和算法具有可行性。

关键词：高铁快巴；混合需求；动态线路；临时站点

中图分类号：U491   文献标志码：A   文章编号：1002-4026（2024）01-0118-10

Dynamic route planning method for a high-speed rail feeder bus based on mixed demand

Abstract∶To meet the needs of passengers for connection and evacuation at high-speed rail stations and enhance the role of high-speed rail stations as urban comprehensive transportation hubs， a dynamic route planning model of a high-speed rail feeder bus is established based on mixed demand that includes reservation and real-time demands. Based on the reservation demand， considering the operation cost of a bus company as well as the travel time cost， the route planning model is established before the start of operation. An improved genetic algorithm was designed using niche methods to solve the problem. After the start of operation， real-time demand can be inserted into the established vehicle route with temporary stations. To realize a dynamic route planning scheme， an integer planning model is established to minimize the variable cost of the system. Using the proposed method，30 demand groups were randomly generated and solved in the Beitaipingzhuang street area， Beijing. Results show that the model can generate an optimal dynamic route planning scheme for a high-speed rail feeder bus in two periods to satisfy the mixed demand. Compared with traditional genetic algorithm， niche genetic algorithm can effectively avoid premature and obtain better results， thus confirming the feasibility of the proposed model and the niche genetic algorithm.

Key words∶high-speed rail feeder bus; mixed demand; dynamic route; temporary station

為提高高铁站的城市综合交通枢纽的地位，满足旅客在高铁站的接驳及疏散需求，出现了一种新型的城市公共交通运营模式——高铁快巴。高铁快巴是以高铁站为接驳站点，采用站内换乘的模式，在常规公共交通运力不足的早晚出行高峰期和夜间运营，服务于选择高铁出行的人群，是一种快速反应式公交[1]。

国内学者对高铁快巴的线路设计规划、车辆调度等运营管理方法等进行了诸多研究。张英群等[2]提出了一种基于交通引导开发（transit oriented development，TOD）理念构建高铁快巴服务网络的方法；安久烨等[3]考虑回程的服务去往，研究高铁车站接驳公交灵活线路的优化设计方法；姚恩建等[4]针对铁路车站夜间乘客疏散问题提出基于定制公交的解决方案，并对其核心的多线路动态规划问题展开研究。

高铁快巴具有“一人一座、预约出行、快速直达”的运营特点，是定制公交的一种模式。近年来国内外学者对定制公交路径优化和车辆调度方面进行了研究，LEE等[5]和BELHAIZA[6]以最小化运营时间或成本、最小化乘客出行时间等为目标，以车辆行程距离或时间、预约时间窗、乘客最大等待时间等为约束，建立数学模型；邵文等[7]进一步考虑乘客乘坐和到达的时间要求，建立兼顾降低成本和乘客满意度的调度模型；程仁辉等[8]考虑乘客心理和道路交通的影响，对定制公交给予一定的拥堵道路停车载客惩罚；赵力萱等[9]通过建立模型和构建算例研究以碳减排为目标的定制公交线路规划问题。路径优化和车辆调度的求解算法，多采用领域搜索算法、分布式算法、遗传算法等。信息采集和交互技术的发展为乘客需求的精细化管理提供了可能，乘客可以提前或实时定制出行需求。国内外学者同样在满足混合需求的定制公交调度方面做了许多研究，QUADRIFOGLIO等[10]提出了一种简单插入算法， 以效用变化最小的为目标， 将乘客逐次插入到每个班次中；邱丰等[11]建立了同时处理静态需求和动态需求的2阶段调度模型；邵孜科等[12]从减少乘客平均出行时间和降低系统拒绝率两个方向出发，对简单插入算法进行优化。

既有研究未考虑乘客需求点的分散性、路网的复杂性和封闭式小区的存在，以及乘客对在车时间、等待时间、步行时间等不同状态下时间的感知差异。在此基础上，本文考虑乘客需求点位于封闭式小区内部等复杂情况，引入临时站点，同时考虑乘客对在车时间、等待时间、步行时间的感知差异，建立基于混合需求的高铁快巴动态线路规划模型，提高响应实时需求预约的成功率。

1 问题描述

按照不同的线路类型和服务模式，高铁快巴分为固定和动态两类运营线路。固定线路是参照常规公交的运营方式；动态线路依托系统支持按照乘客需求动态响应，自动规划生成车辆行驶路径[13]。

本文研究的对象为高铁快巴动态运营线路，该模式线路在高铁站与一定范围内的乘客居住区之间运行，在居住区内部有调度站。本文将车辆发车前收到的预约定义为提前预约需求，将车辆发车后收到的预约定义为实时需求，车辆运行方向为乘客居住区至高铁站，建立基于混合需求的动态线路规划模型。车辆发车前，

乘客选择一个固定站点作为出行起点、高铁站作为出行终点，调度中心接收提前预约信息集合，生成多车辆行驶路线和时刻表信息，其中一辆车的行驶路线如图1（a）所示。车辆发车后以既定路线行驶，乘客可定位其当前所在位置为出行起点、高铁站作为出行终点，调度中心收到实时需求Q1、Q2，由于

Q1、Q2所在位置不适宜作为站点，将Q1、Q2引导到临时站点上车，实时调整车辆行驶路線，将车辆行驶路径和延误信息反馈给乘客，此阶段车辆行驶路线调整为图1（b）。

2 模型建立基础

2.1 基本假设

从实际问题中构建模型，作如下假设：

（1）车辆均从居住区内的调度站出发，响应乘客需求后通过城市快速路直达高铁站。

（2）每两个固定站点或临时站点间均可以通达，站点之间的距离固定。公交车辆在任一两个站点之间以一定速度匀速行驶，在每个站点的停留时间相等。

（3）满足所有提前预约乘客需求，但不一定满足所有实时乘客需求。

（4）由于响应实时需求会增加既定的行程时间，设置tr为单程松弛时间，单程增加的行程时间不能超过tr。

（5）提前预约乘客可预约出发和到达时间窗，实时需求乘客期望预约后尽快接受服务。

（6）为保持较高的服务质量，实行一人一座。

（7）临时站点位置由调度系统根据路网情况实时生成。

2.2 乘客时间窗分析

考虑到接驳高铁客流的特点，乘客对于到达时间的准时性要求更高。到达时间为硬时间窗，若乘客到达时间不在期望时间窗内时，乘客放弃高铁快巴出行，故将到达时间窗作为模型的约束。乘客出发时间为软时间窗，软时间窗乘客满意度函数如图2所示。为反映乘客对出发时间满意度的变化，构建惩罚函数来反映满足乘客时间窗的程度，函数图像如图3所示。

乘客出发时间惩罚函数g（t）为

式中：［Et，Lt］为乘客期望出发时间窗；［Et′，Lt′］为乘客可忍受出发时间窗；η、λ均为单位时间惩罚系数，且η>λ。

3 基于混合需求的高铁快巴动态线路规划模型

3.1 基于提前预约需求的线路规划模型

由于高铁快巴为社会提供公共服务，公交公司应综合考虑运营成本和满足乘客出行成本。达到系统最优时，公交运营成本、乘客出行成本和乘客时间窗惩罚的总和最小，目标函数可表示为

式中：N为固定站点集合；V为调度站集合；H为高铁站集合；K为车辆集合；N（k）为车辆k经过的站点的集合；Qi为i站点上车需求集合；f为乘客出行时间成本；c0p为车型p的公交车辆启动成本；c1p为车型p的公交车辆单位距离运输成本；qmaxp为车型p的公交车辆座位数；qα为预留座位数；dmax为车辆单程最大行驶距离；dij为站点i和j间的实际距离；p（k）为车辆k的车型；oki为车辆k离开i站时的载客人数；tki为车辆到达站点i时间；tqi为站点i的第qi个乘客接受服务的时间；tα为车辆在站点最小服务时间；tr为单程松弛时间;tlateqi为站点i第qi个乘客的可忍受最晚到达时间；车辆k从站点i到站点j时，xkij为1，否则xkij为0；站点i的第qi个乘客由车辆k提供服务时，ykqi为1，否则ykqi为0。

式（2）为模型的目标函数，为车辆固定成本、车辆变动成本、乘客出行时间成本、乘客时间窗惩罚值之和；式（3）表示车辆从调度站出发；式（4）表示车辆最终到达高铁站；式（5）表示固定站点至少由一辆车进行服务；式（6）表示一辆车不能重复经过某个站点；式（7）表示满足所有提前预约乘客；式（8）表示乘客只能由经过其预约站点的车辆提供服务；式（9）为考虑预留座位的载客量约束；式（10）为单程行驶距离约束；式（11）为考虑车辆单程松弛时间下的乘客到达时间窗约束。

该问题可转化为旅行商（TSP）问题，即所有需求点仅被经过一次且需求均被满足的车辆路径问题。将同一个站点不同的需求进行拆分，生成相应的虚拟站点。这些虚拟站点的位置信息与其真实站点相同，将虚拟站点放入需求站点集合N中，并将模型约束式（5）调整为式（12）。

3.2 考虑实时需求的动态线路规划模型

系统因满足实时需求，增加的系统变动成本包括车辆变动成本、预约乘客的时间成本和实时需求乘客的时间成本。由于乘客倾向认为与在车的时间成本相比，等待和步行的时间成本更大，且步行消耗体力更大，本文引入转换系数表示这一感知差异，三者的转换系数由大到小为：步行时间转换系数、等待时间转换系数、在车时间转换系数。模型的目标为最小化系统变动成本，即

式（13）为目标函数，求解系统增加的车辆变动成本、提前预约乘客增加的出行时间成本、实时预约乘客的出行时间成本之和最小的系统响应方案；式（14）为所有提前预约乘客增加的等价出行时间计算公式，为在车时间和等待时间之和；式（15）为该实时需求乘客的等价出行时间计算公式，为在车时间、等待时间和步行时间之和；式（16）表示每个可响应的实时需求在一个响应站点由一辆车提供服务。

4 算法设计

4.1 基于提前预约需求的线路规划模型的求解算法

遗传算法是一种基于概率统计的随机搜索算法，对求解TSP问题具有一定的优势，本文用遗传算法求解基于预约需求的线路规划模型。

4.1.1 编码与解码

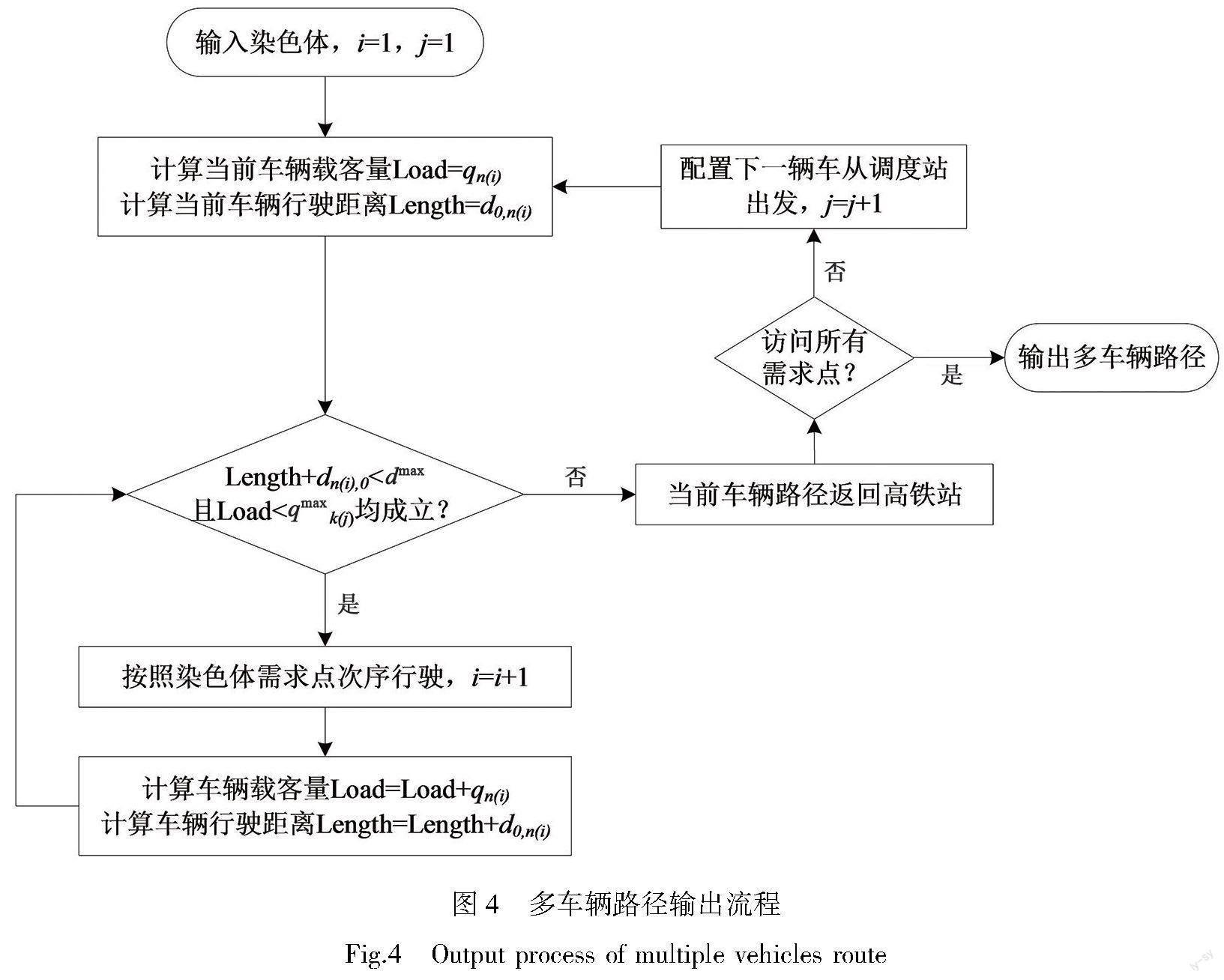
采用整数排列编码方法编码种群的染色体。每条染色体分为N+K段，其中N为对应需求点的编号，K为每辆车车型编号。利用式（9）载客量约束和式（10）单程行驶距离约束将一条所有站点访问顺序染色体转化为多辆车路径信息，该过程如图4所示。

4.1.2 计算适应度函数

通过解码得到的多车辆路径满足约束式（3）～ （10），为满足乘客到达硬时间窗约束，即约束式（11），构造适应度函数为

i=1/（Fi+Mi），（17）

式中：i为个体i的适应度；Fi为个体i的目标函数；Mi为硬时间窗惩罚值，当所有预约需求满足约束式（11）时，Mi=‘0，否则Mi=‘10 000。

4.1.3 更新适应度函数

本文利用小生境技术对传统遗传算法进行改进，通过共享函数调整适应度使较低适应度的个体被淘汰的概率增大，使得适应度较高的个体得以保留 [14]，更新个体适应度值′i的计算公式如下

式中：ωi，j为个体i与个体j的共享函数；σ为峰半径；α控制共享函数的形状，通常取α=1，表示线性共享函数；l（i，j）为个体i与个体j之间的欧氏距离；Si为个体i的共享度；π为遗传算法种群个体集合。

4.1.4 求解步骤

遗传算法的其他遗传操作与传统遗传算法相似，算法步骤如下。

Step1：初始化。设计遗传算法染色体的编码方案，确定参数，如种群规模、最大进化代数、交叉概率、变异概率、小生境技术参数等，生成满足模型约束的初始种群。

Step2：解码染色体，进行适应度计算和更新。

Step3：终止判定。如果进化代数达到最大进化代数，则停止算法，解码染色体，输出最优解的函数值、车型配置及线路路径；否则转step4。

Step4：进行遗传操作。执行选择、交叉、变异和逆转，转Step2。

4.2 实时需求响应机制

可响应实时需求的备选车辆为实时需求生成时刻正在运行或等待运行的车辆，备选响应站点为临时需求周边具备停车条件的临时站点，则当每个实时需求生成时，系统响应步骤如下。

Step3：枚举法求解动态线路规划模型，生成响应方案，调整线路方案，将信息反馈给司机和乘客。

5 案例分析

5.1 案例区域及参数取值

本文选择北京市北太平庄街道辖区南部地区为高铁快巴的服务区域，该区域以住宅用地为主，商业用地、办公用地及绿化设施用地为辅。根据道路条件和客流调研，设置13个固定站点和若干个临时站点，调度站位置在积水潭地铁站，终点站为北京南站。案例区域示意图见图5。模型参数取值如下[15-18]：vwalk=1.5m/s，f=12元/h，η=‘1.5元/min、γ=‘0.5元/min；β1=‘1.1，β2=‘1.2，β3=‘1.5；本文采用载客量为9人和14人的小型公交车，经估算qmax1=‘9，c01=‘50元/辆，c11=‘0.003元/m，qmax2=14，c01=‘70元/辆，c11=‘0.005元/m；dmax=20 km；在北太平庄街道区域内车辆vbus=‘15 km/h，在城市快速路上vbus=30 km/h；其他參数根据实际调研和需求赋值，qα=‘3，tα=‘30 s，tr=5 ‘min，第一辆车的发车时间为早7：00，发车间隔为10 min；模拟30组早高峰时段预约和实时需求，提前预约乘客的期望出发时间窗为2 min，可忍受出发时间为提前或推迟3 min范围内。其中一组需求见表1和表2，实时需求的位置见图5。

5.2 模型与算法的有效性验证

设计3组对比试验：A组为使用本文模型和算法的基本组；B组为使用本文模型、传统遗传算法的对照组，与A组结果对照来验证本文使用的小生境遗传算法的可行性与适应性；C组为在响应实时需求时取消临时站点、使用本文模型和算法的对照组，与A组结果对照来验证设置临时站点的合理性。对30组需求进行求解并进行对比试验，所有试验都在最大进化代数内收敛，结果见表3。A组与B组相比，系统成本降低3.4%，人均成本降低3.3%，得到的线路规划结果更优，证明小生境遗传算法有效避免传统遗传算法易陷入局部最优解的缺陷。A组与C组相比，实时需求响应率由54.6%提升至89.4%；由于A组服务的乘客更多，系统总成本稍高于C组；A组与C组相比，人均成本降低4.1%，说明临时站点的设置使响应方案更加柔性化，在大幅度提高响应率的同时降低了系统人均成本，具有经济性。

5.3 车辆动态线路规划结果

以表1～2中的需求为例，采用本文模型与算法进行车辆动态线路规划，算法在第117代完成收敛，优化过程如图6所示，高铁快巴在北太平庄区域内行驶路线图如图7，高铁快巴动态线路规划方案如表4所示，所有实时需求均能被响应。

6 结论

高铁快巴作为一种定制公交运营模式的绿色出行方式，满足旅客在高铁站的接驳及疏散需求，增强高铁站作为城市综合交通枢纽的作用。本文研究基于混合需求的高铁快巴动态线路规划模型，以系统总成本和变动成本最小为目标，建立基于提前预约需求和考虑实时需求的高铁快巴动态线路规划模型。案例验证了本文模型在提供更便捷灵活的线路规划方法的同时，可以提高实时需求响应率，降低系统人均成本；设计的小生境遗传算法可以保证种群多样性，提高进化效率，得到更优的结果。本文的案例是基于小规模需求，未来可在大规模需求中进行试验，进一步验证模型算法的可行性，并进一步精细考虑乘客预约时间要求，提高乘客满意度。

参考文献：

［1］李佳晖， 宋瑞， 郭小乐. 高铁快巴运营效果综合评价指标体系研究[J]. 大连交通大学学报， 2018， 39（4）： 1-6. DOI： 10.13291/j.cnki.djdxac.2018.04.001.

[2]张英群， 宋瑞， 何世伟， 等. TOD理念下高铁快巴服务网络设计研究[J]. 铁道学报， 2019， 41（9）： 12-19. DOI： 10.3969/j.issn.1001-8360.2019.09.002.

[3]安久煜， 宋瑞， 毕明凯， 等. 高铁车站接驳公交灵活线路优化设计研究[J]. 交通运输系统工程与信息， 2019， 19（5）： 150-155. DOI： 10.16097/j.cnki.1009-6744.2019.05.021.

[4]姚恩建， 马斯玮， 向镇， 等. 面向铁路夜间乘客疏散的定制公交线路优化[J]. 北京交通大学学报， 2021， 45（1）： 78-84. DOI： 10.11860/j.issn.1673-0291.20200046.

[5]LEE A L， SAVELSBERGH M. An extended demand responsive connector[J]. EURO Journal on Transportation and Logistics， 2017， 6（1）： 25-50. DOI： 10.1007/s13676-014-0060-6.

[6]BELHAIZA S. A data driven hybrid heuristic for the dial-a-ride problem with time windows[C]//2017 IEEE Symposium Series on Computational Intelligence （SSCI）. Honolulu， HI， USA： IEEE， 2017： 1-8. DOI： 10.1109/SSCI.2017.8285366.

[7]邵文， 贾顺平， 曹文娟. 基于混合车型的灵活型接驳公交路径协同优化研究[J]. 山东科学， 2019， 32（4）： 64-73. DOI： 10.3976/j.issn.1002-4026.2019.04.009.

[8]程仁辉， 贾顺平. 考虑拥堵道路停车惩罚的定制公交调度研究[J]. 山东科学， 2021， 34（1）： 53-61. DOI： 10.3976/j.issn.1002-4026.2021.01.007.

[9]赵力萱， 吴泽驹， 何康园， 等. 碳减排背景下定制公交路线规划方法[J]. 交通运输研究， 2022， 8（3）： 56-65. DOI： 10.16503/j.cnki.2095-9931.2022.03.006.

[10]QUADRIFOGLIO L， DESSOUKY M M， PALMER K. An insertion heuristic for scheduling Mobility Allowance Shuttle Transit （MAST） services[J]. Journal of Scheduling， 2007， 10（1）： 25-40. DOI： 10.1007/s10951-006-0324-6.

[11]邱豐， 李文权， 沈金星. 可变线路式公交的两阶段车辆调度模型[J]. 东南大学学报（自然科学版）， 2014， 44（5）： 1078-1084. DOI： 10.3969/j.issn.1001-0505.2014.05.036.

[12]邵孜科， 张泉， 王树盛， 等. 可变线路公交车辆调度算法优化研究[J]. 交通信息与安全， 2018， 36（5）： 83-89. DOI： 10.3963/j.issn.1674-4861.2018.05.011.

[13]万逸飞， 吴天真. 需求、平台、供给——创新驱动公交服务新模式：北京公交高铁快巴的思考与实践[J]. 人民公交， 2018（7）： 54-55. DOI： 10.16857/j.cnki.cn11-5903/u.2018.07.008.

[14]GOLDBERG D E. Genetic algorithms in search， optimization， and machine learning[M]. Reading， Mass.： Addison-Wesley Pub. Co.， 1989.

[15]闫平， 宋瑞. 城市公共交通概论[M]. 北京： 机械工业出版社， 2011.

[16]孙杨， 孙小年， 孔庆峰， 等. 轨道交通新线投入运营下常规公交网络优化调整方法研究[J]. 铁道学报， 2014， 36（3）： 1-8. DOI： 10.3969/j.issn.1001-8360.2014.03.001.

[17]范文豪. 需求响应式接驳公交路径优化模型研究[D]. 南京： 东南大学， 2017.

[18]沈犁， 杨京帅， 王周全， 等. 城市机动式辅助客运方式时间效用改进[J]. 长安大学学报（自然科学版）， 2016， 36（4）： 95-102. DOI： 10.19721/j.cnki.1671-8879.2016.04.013.