分数阶CEV模型下未定权益的紧致差分法
2024-02-24喻喜沩孙玉东
胡 青,喻喜沩,孙玉东
(1.贵州民族大学 数据科学与信息工程学院,贵阳 550025; 2.贵州民族大学 政治与经济管理学院,贵阳 550025)
金融界中存在多种风险,投资者的任何一笔投资在未来都可能是一个未定权利.面对风险,常利用期权替换掉不利的风险,保留有利的风险.期权价格依赖于标的资产价格,是交易双方之间的一种合约,它赋予买方某种形式的权利,使得他可以在未来某一时间以某一固定的价格购买或出售某标的资产.未定权益定价主要以BS模型为基础.近年来,分数阶微分方程在科学等许多不同领域获得了重要意义. 一般来说,分数阶微分方程的解析解难以求解,甚至是没有解析解.因此利用数值技术来求解这些问题是必要的. BS方程是典型求解欧式期权定价的偏微分方程, 分数阶BS模型下期权定价带来更大的便利,为此许多学者提出多种求解分数阶BS模型下期权定价的技术[1-4]. 田朝微,李锦成[5]等人采用紧致有限差分格式研究了BS模型下欧式看跌期权的定价问题.龙敏,孙玉东[6]采用加权差分格式研究了时间分数阶CEV模型下的算术亚式期权. 张琪,左平[7]等人运用有限差分法研究了美式多资产定价问题. BS模型过于严格的假设使其在理论和应用上存在缺陷, CEV模型很好地解决BS模型中存在的不足,大量学者已经对该模型下的期权定价进行了研究[8-11].
本文在文献[4]的思想上,运用紧致差分来求解分数阶CEV模型下未定权益的数值解.首先在时间上采用Caputo分数阶导数进行离散,空间上采用4阶紧致差分格式,通过傅里叶分析法和数学归纳法验证该方法的稳定性和收敛性,得到该方法是无条件稳定的,且是O(t2-α+Δx4)收敛.所考虑以下的分数阶CEV模型[1]
(S,τ)∈R+×(0,T), 0<α<1,
(1)
边界条件和初始条件分别为

C(S,T)=φ(S),
(2)

下面将通过变量的转换和空间截断,很好地求出分数阶CEV模型(1)-(2)的解.将采用变量变换和空间截断的方法对式(1)、(2)进行调整.
1 时间分数阶CEV模型下欧式未定权益的数学模型
为了能推导出紧致差分格式,本节通过变量变换对模型进行简单处理.设式(1)、(2)中变量S=ex,τ=T-t,有z(x,t)=C(ex,T-t),得到以下分数阶CEV模型
z(-∞,t)=φ(t),z(∞,t)=Ψ(t);
z(x,0)=f(x)
(3)
(4)
为了方便数值求解分数阶CEV模型(3),将无限空间截断为有限空间,满足方程
h(x,t),(x,t)∈(xA,xB)×(0,T),
z(xA,t)=φ(t),z(xB,t)=Ψ(t);z(x,0)=f(x),
(5)
其中:δ=σ2exp(2αx-2x)/2,β=r-δ,且r>0
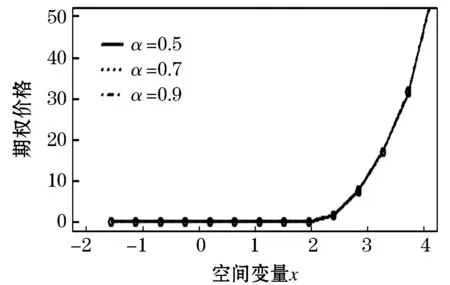
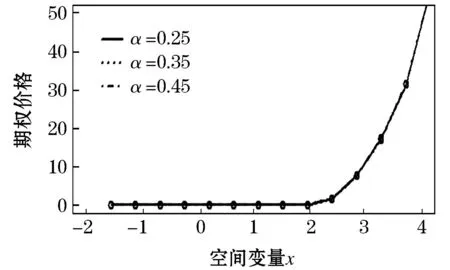
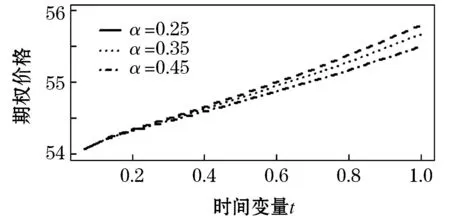
根据变量变换,得到分数阶CEV模型(5).其次,分别对该模型在时间上和空间上进行离散.首先,在时间上采用Caputo分数阶导数对式(5)在[0,T]内进行离散. 令0=t0 (6) 引理1[13]式 (6)中bl满足以下关系 1)b0=1; 2)bl>0, 0≤l≤N; 3)bl-1>bl, 1≤l≤N. 上述采用了Caputo导数对时间离散,将构造4阶紧致差分格式对空间离散. 为求解方程(5),本文通过构造一种紧致差分格式来近似该模型,并结合边界条件和初始条件求解模型.本节借鉴文献[4]中的思想,构造紧致差分格式来对空间进行离散.紧致差分格式具有高精度和稳定性,且具有小的离散子域、处理边界单元时无特殊困难.因此,在空间上采用该方法对式(5)在[xA,xB]进行离散. 首先,令M={xA=x0 i=1,2,…,I-1, (7) i=1,2,…,I-1, (8) 定理1 考虑下列微分方程 (9) 得到微分方程的4阶紧致差分格式 i=1,2,…,I-1, 其中: 证明:结合式(7)、(8) ,则微分方程在x=xi处的差分形式有 (10) 其中: 分别对 式(9)求导,进一步逼近γ1中的z(3)(xi)和z(4)(xi),并代入到γ1中.在x=xi处,有 将式(7)、(8)代入到上式中,有 (11) i=1,2,…,I-1, 证毕. (12) h(x,t)-y(x,t). (13) 根据定理1, 其中a=-δ,b=-β,c=-r,则式 (13)在点(xi,tj)表示为 (14) 误差项为R(xi,tj)=O(t2-α+Δx4).离散边界条件和初始条件,得到如下形式 (15) (16) (17) (18) Q*Hj+Wj, 1≤j≤N, (19) 其中: 分别对问题(5)在时间和空间上离散,得到方案(16) .将对该方案进行理论分析. 通过上述的推导过程,得到问题(5)的一种紧致差分格式,即得到方案(16),现对该方法进行稳定性和收敛性分析. (20) j=0,1,…,N (21) (22) (23) 因此,式(22)可以简化为以下形式 上式两边同时取绝对后,因为Δx>0,Δt>0和0<α<1,所以Γ(2-α)>0和d>0因此,有p1>0,p2>0,p3>0,p4>0,满足下列不等式 (24) 进而推出 (25) 定理2 针对问题(5)所得到(16) 的数值格式是无条件稳定的. 证明:首先证明|ξj|≤|ξ0|.假设当j=1时,式(25)有|ξ1|≤b0|ξ0|.由于b0=1,则可以得到|ξ1|≤|ξ0|.因此,当j=1时,|ξj|≤|ξ0| 成立.接下来,假设|ξj|≤|ξ0|在j≤n-1时也成立,有|ξj|≤|ξ0|,j=1,2,…,n-1.当j=n时, 式(25)变为 其次,根据|ξj|≤|ξ0|,j=1,2,…,n-1,则上述不等式满足 =b0|ξ0|. 由于b0=1,则上述方程可以简化为|ξn|≤|ξ0|因此, 当j=n时, |ξj|≤|ξ0|也是成立的.综上所述, 通过数学归纳法,|ξj|≤|ξ0| 对于每一个j都是成立的, 即|ξj|≤|ξ0|,j≥1.最后,结合误差范数,即式(21),可以推出 即‖rj‖2≤‖r0‖2.综上,针对问题(5)所提出(16)的数值格式是无条件稳定的.证毕. (26) (27) (28) M1(Δt2-α+Δx4),j=1,2,…,N, (29) 上述等式和式(27)中级数部分是收敛的.存在一个正常数M2,使得 |σj|≡|σj(k)|≤M2Δt|σ1|≡ M2Δt|σ1(k)|,j=0,1,…,N. (30) 以上是陈述和证明了该方法主要部分的收敛性. 定理3 假设z(x,t)是问题 (5)的精确解,则数值格式 (14)是l2收敛的,且解满足 ‖εj‖2≤M(Δt2-α+Δx4). 证明:将采用数学归纳法证明下列方程. |μj|≤M2(1+Δt)j|σ1|,j=1,2,…,N. (31) 在式 (28)中假设j=1,结合|(p1+ωp2)+(p3-ωp4)|-1≤1.有 |σ1|≤M2(1+Δt)|σ1|. 因此,式 (31)在j=1时成立.接下来,假设式(31)在j≤n-1时,也是成立的,有 |μj|≤M2(1+Δt)j|σ1|,j=1,2,…,n-1. (32) 当j=n时,结合式 (24)且|(p1+ωp2)+(p3-ωp4)|-1≤1,得到 将式(32)、(30)代入到上述不等式中,可以得到 M2Δt|σ1|≤M2(1+Δt)n|σ1|. 因此,当j=n时,式(31)是成立的.综上所述,通过数学归纳法,式(31)对于每一个j都是成立的.现在,结合式(27),(29) 和(31),可以得到 M2(1+Δt)j‖R1‖2≤M1M2ejΔt(Δt2-α+Δx4). 由于jΔt≤T,上述公式可以变为‖εj‖2≤M(Δt2-α+Δx4),M=M1M2eT.证毕. 本节以欧式看涨期权期为例,研究所提出的方法对分数阶CEV模型下欧式看涨期权进行定价,通过变换参数,分析对欧式看涨期权定价的影响,来证明紧致差分格式的实用性.运用R软件模拟,考虑以下模型 rC(S,τ)=0,(S,τ)∈(0.1,100)×(0,1) 设定初边值条件分别为 C(S,T)=max{S-K,0};C(0.1,τ)=0, C(100,τ)=100-Kexp(-r(1-τ)). 固定参数r=0.05,K=10和T=1 a.讨论参数α和σ取不同值时,期权定价的变化,见图1、2. 图1 不同α下的期权价格 图1设定σ=0.25时,根据分数阶参数α分别为0.5、0.7和0.9时,绘制出资产价格与期权定价的变化图.数值结果表明,在空间上期权价格随着资产价格的增大而增大.其中,当空间变量x=2时,期权价格明显增加.图2设定α=0.5时,根据参数σ分别为0.25、0.35和0.45时,描绘出资产价格与期权定价的变化.同样得到在空间上随着资产价格的增大期权价格也增大,当空间变量x=2时,期权价格增长迅速. 图2 不同σ下的期权价格 图3固定σ=0.25时,根据分数阶参数α分别为0.5、0.7和0.9时,描绘出资产价格与期权定价的变化图.从图中可以看出,在时间上期权价格随着资产价格的增大而增大.其中,分数阶参数α越小时,图像越陡峭;反之分数阶参数α越大时,图像越平缓. 图4固定α=0.5时,根据参数α分别为0.25、0.35和0.45时,描绘出资产价格与期权定价的变化图.数值结果显示,同样的在时间上随着资产价格的增大期权价格也增大.与分数阶参数α相比, 参数α的变化对期权价格的影响较小. 图3 不同α下的期权价格 图4 不同σ下的期权价格 本文提出一种关于求解分数阶CEV模型下未定权益的紧致差分格式,讨论该格式是无条件稳定的,也证明该格式是O(t2-α+Δx4)收敛.并且以欧式看涨期权为例,验证该紧致差分格式的实用性.结果显示,期权价格明显受分数阶导数影响.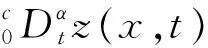

2 欧式未定权益的紧致差分格式
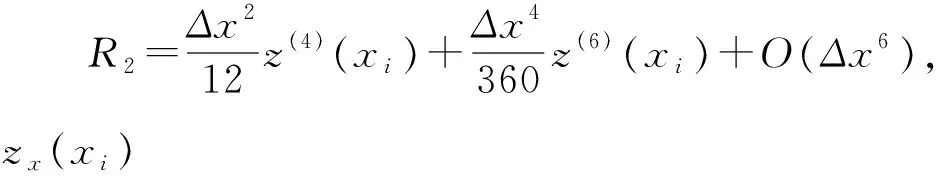
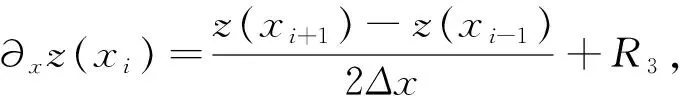
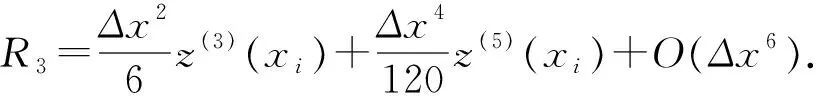
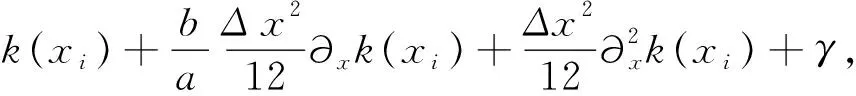

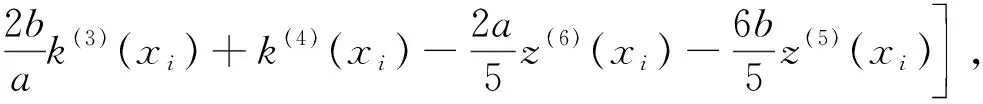
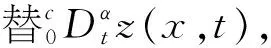

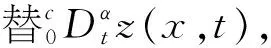
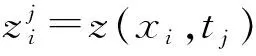
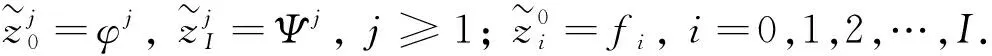
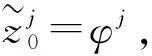
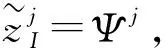
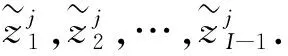
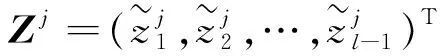

3 稳定性和收敛性分析
3.1 稳定性分析
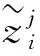
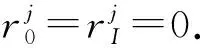


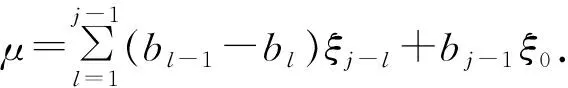
3.2 收敛性分析
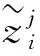

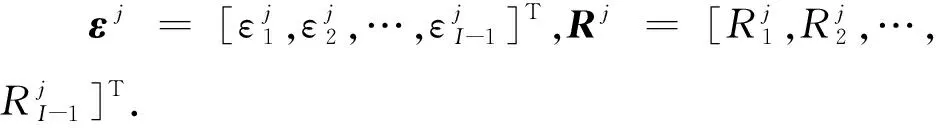
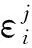

4 数值实验
5 结 语
