禁用两个子图的图的全控制数

杨树承, 胡夫涛, 张昶旭

(安徽大学 数学科学学院,合肥 230601)

1 研究背景

本文中的图G=(V(G),E(G))是顶点集为V(G),边集为E(G)的无环且无重边的简单无向图,图G的任一顶点v,其开邻域N(v)为在G中和点v相邻的所有点的集合,闭邻域记为N[u]=N(u)∪{u}.顶点v的度是指与v相邻点的数目,记为d(v)=|N(v)|.如果顶点v的度为0,则称它为孤立点.图G中点的度的最小值和最大值为图G的最小度和最大度, 分别用δ(G)和Δ(G)表示.如果图的顶点数目|V(G)|=n, 则称图G为n阶图.通常用e=uv表示G中的一条边,其中u和v是e的两个端点, 称u和v是邻接的, 记为u～v.如果图G的任意两个点都有路相连,则称图G为连 通图.设S⊆V,称顶点集为S, 边集为G中两个端点都在S中的图为由S生成的导出子图,记为〈U〉.没有给出定义的基本符号和图论术语[1].把n个顶点顺次连接起来形成的图称为路, 记为Pn.含有n个点的完全图, 记为Kn, 是指任意两个顶点都邻接的简单图.如果一个图G的顶点集可以被划分成两个子集X,Y, 并且每条边一端点在X中另一个端点在Y中, 那么G称为二部图, 记作G[X,Y].如果图G[X,Y]在集合X中的每一个顶点都和Y中的每一个顶点邻接,则称G为完全二部图, 设|X|=s,|Y|=t, 完全二部图G表示为Ks,t.特别的K1,3称为爪图, 见图1.

图1 爪图K1,3.Figure1 Claw graph K1,3

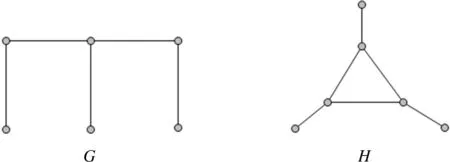
图2 图G是E图,图H是网图Figure 2 Graph G was E graph,graph H was net graph

图3 D图Figure 3 D graph

设D是V的子集.若不在D中的每个点都至少和D中一点相邻, 则称D为G的控制集.最小控制集所含的顶点数称为图G的控制数,记为γ(G).根据实际需要, 还引申出很多其他变形的控制.如果不含孤立点的图G的控制集D的导出子图〈D〉不含孤立点, 则称D为G的全控制集.图G的最小全控制集含有的顶点数称为全控制数, 记为γt(G).Pfaff等[2]证明了求解图的全控制数是NP-完备的.

图的控制数的研究可以追溯到1850年.图的控制问题和相关子集问题的研究是图论研究中心热点,引起了人们广泛的研究, 相关研究成果有几千篇论文[3-6].在图的控制论中,图的全控制是研究比较多的.Henning于2009年撰写了一篇图的全控制问题的综述[7].

对于无爪图的全控制数的研究有很多[8-9].对于禁用两个子图的图的全控制数研究暂时还未见到.本文考虑了禁用爪图和D图的N≥2阶连通图G全控制数得到γt(G)≤2「n/4⎤.

2 主要结论

设G=(V,E)是一个简单无向图,u是V中任一点和X是不包含u的顶点子集.记d(u,X)是G[X∪{u}]中最长的以u为端点的路的长度.设S⊆V,记

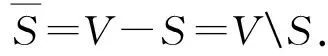
引理2.1 如果P=v1v2…vl是G中的一条最长路,则对任意i∈[l-1],

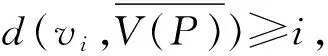
对于禁用两个子图的图的成对控制数研究暂时还未见到.本文得到了无爪图和无D图时全控制数的上界.

定理2.1 设G是n≥2阶连通无爪和无D的图,则γt(G)≤2「n/4⎤.

证明：首先考虑n≤6的情形.设u是G中的一个最大度点.当Δ(G)≤n-2时,G至多有一个点v不与u相邻,此时这样的点v一定与u的某个邻点w相邻,则{u,w}是G的一个全控制集,所以γt(Pn)≤2.当Δ(G)=2时,G是阶数为n的路Pn,此时γt(Pn)≤2「n/4⎤.剩余的情况为n=6且d(u)=3.设G不与u相邻的两个点为s,t.若s～t,则{u,w,s,t}是G的一个全控制集,所以γt(G)≤4.若点s与点t不相邻,则{u,s′,t′,t}是G的一个全控制集,其中s′∈N(s)∩N(u),t′∈N(t)∩N(u),所以γt(G)≤4.

下面设n>6.下证总是存在U⊆V(G),|U|=m且4≤m≤6,〈U〉是连通的,使得γt(〈U〉)≤「m/2⎤且〈V-U〉是连通的.此时根据归纳法原理γt(G)≤γt(〈U〉)+γt(〈V-U〉)≤2「m/4⎤+2「n-m/4⎤≤2「n/4⎤.

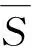
N(v1)⊆S,

N(v2)⊆S.

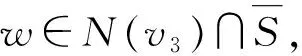
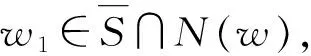
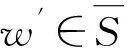
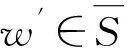
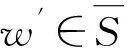
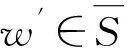
情形1v1～v3.N(w)∩{v1,v2,…,v6}=Ø且N(v1)∩{v4,v5,v6}=Ø.

取U={v1,v2,v3,v4,w},〈U〉是连通的,γt(〈U〉)=2且〈V-U〉是连通图.

情形2v1～v7.N(w)∩{v1,v2,…,v6}=Ø且N(v1)∩{v3,v4,v5,v6}=Ø.

取U={v2,v3,v4,w},〈U〉是连通的,γt(〈U〉)=2且〈V-U〉是连通图.

情形3v2～v4.N(w)∩{v1,v2,…,v6}=Ø且N(v1)∩{v3,v4,v5,v6,v7}=Ø.

取U={v1,v2,v4,w},〈U〉是连通的,γt(〈U〉)=2且〈V-U〉是连通图.

情形4v2～v5.N(w)∩{v1,v2,…,v6}=Ø,N(v1)∩{v3,v4,v5,v6,v7}=Ø,N(v2)∩{v4}=Ø.

由于〈v2,v4,v5,v6〉不是爪图,一定有v2～v6或v4～v6.分以下2种情形考虑.

1)v2～v6

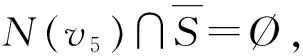
2)v4～v6

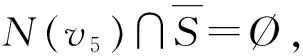
情形5v2～v6.N(w)∩{v1,v2,…,v6}=Ø,N(v1)∩{v3,v4,v5,v6,v7}=Ø,N(v2)∩{v4,v5}=Ø.

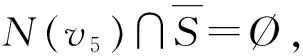
情形6v2～v7.N(w)∩{v1,v2,…,v6}=Ø,N(v1)∩{v3,v4,v5,v6,v7}=Ø,N(v2)∩{v4,v5,v6}=Ø.

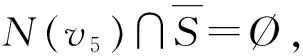
情形7v3～v6.N(w)∩{v1,v2,…,v6}=Ø,N(v1)∩{v3,v4,v5,v6,v7}=Ø,N(v2)∩{v4,v5,v6,v7}=Ø.

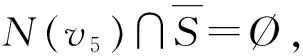
情形8v3～v7.N(w)∩{v1,v2,…,v6}=Ø,N(v1)∩{v3,v4,v5,v6,v7}=Ø,N(v2)∩{v4,v5,v6,v7}=Ø,N(v3)∩{v6}=Ø.

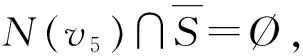
情形9v4～v6.N(w)∩{v1,v2,…,v6}=Ø,N(v1)∩{v3,v4,v5,v6,v7}=Ø,N(v2)∩{v4,v5,v6,v7}=Ø,N(v3)∩{v6,v7}=Ø.

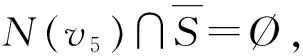
情形10v4～v7.N(w)∩{v1,v2,…,v6}=Ø,N(v1)∩{v3,v4,v5,v6,v7}=Ø,N(v2)∩{v4,v5,v6,v7}=Ø,N(v3)∩{v6,v7}=Ø,N(v4)∩{v6}=Ø.

由于〈w,v3,v4,v7〉不是爪图,所以v3～v7.由于v3～v7已经在情形8中进行了详细的讨论,这里不再赘述.

情形11v5～v7.N(w)∩{v1,v2,…,v6}=Ø,N(v1)∩{v3,v4,v5,v6,v7}=Ø,N(v2)∩{v4,v5,v6,v7}=Ø,N(v3)∩{v6,v7}=Ø,N(v4)∩{v6,v7}=Ø.

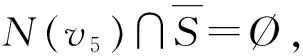
3 结 语

注意到,对于至少含两个点的路Pn,γt(Pn)≤2「n/4⎤.显然路是不含爪和D的图,因此定理2.1给出的上界是紧的.

对于n阶无爪连通图G的全控制数的研究非常多,2000年,Favaron和Henning[10]证明了:若δ(G)≥3, 则γt(G)≤n/2.2007年, Stephan和Anders[11]证明了:δ(G)≥4,则γt(G)≤3n/7.对于有两个禁用子图的全控制数研究还比较少,本文给出了无爪图和不含D图的全控制数的上界.此后可以考虑禁用其他两个子图的全控制数的上界问题,比如禁用一些比D图更大一点的子图.