变系数部分非线性模型的分位数回归估计
2024-02-24梁美娟罗双华张成毅
梁美娟,罗双华,张成毅
(1. 西安工程大学 理学院, 西安 710048; 2. 西安交通大学 经济与金融学院, 西安 710049)
为了能够获得响应变量和协变量之间更多的复杂关系,LI和 MEI[1]在变系数部分线性模型的基础上提出了变系数部分非线性模型,其标准形式为
Y=XTα(U)+g(Z,β)+ε,
(1)
其中:(X,Z)∈Rp×Rq和U∈R是协变量,Y是响应变量,α(·)=(α1(·),…,αp(·))是未知系数函数,g(·,·)是给定的非线性函数,β=(β1,…,βs)T是未知参数向量,且β和Z不一定有相同的维数,ε是期望为零,方差为σ2的随机误差,且与(U,X,Z)相互独立.该模型具有灵活的解释性,还能避免一些高维数据带来的不便,因此成为当今研究的热门话题.文献[1]给出了模型的参数与非参的截面非线性最小二乘估计.目前,已有一些统计学者对模型(1)做了许多研究.纵向数据是指对同一个受试个体在不同时间点上重复观测若干次,从而得到的由截面数据和时间序列数据结合在一起的数据.它在经济学、生物医学、传染病学以及其他的自然科学领域都有着广泛的应用,受到统计学家们的广泛关注.如LIU[2]研究了纵向数据下的变系数变量误差模型;YAN等[3]针对纵向数据对部分线性误差模型进行了经验似然推断.然而,在研究纵向数据时,其中一些数据可能会丢失,所以对于一些缺失数据的处理是统计学家关注的热点.处理随机缺失最常用的方法有完全数据法、逆概率加权法和插补法等.XU等[4]利用逆概率加权法研究了协变量随机缺失的变系数部分非线性变量误差模型;WANG等[5]提出一个逆概率加权轮廓非线性最小二乘估计协变量缺失的变系数部分非线性模型中未知参数和非参数函数.除此之外,文献[6-8]也有研究.对于回归模型的估计问题,大多是基于最小二乘回归法,最小二乘法效果虽然很好,但当数据存在显著的异方差,或者存在尖峰、厚尾等情况时,最小二乘估计的稳健性比较差.因此,人们在使用经典方法的同时,也在不断地探索更好的方法.KOENKER和 BASSETT[9]提出的分位数回归,不需要对误差项的分布作假设,适应性更强.TANG等[10]结合分位数信息和最小二乘方法方程构造无偏估计方程来提高模型的估计效率;YANG等[11]针对变系数部分非线性模型采用分位数回归估计并且进行了变量选择;TANG等[12]研究了协变量随机缺失的变系数复合分位数模型的估计问题.基于以上研究,针对纵向数据缺失情况的变系数部分非线性分位数回归模型的估计还有很多问题值得研究.因此,本文考虑使用逆概率加权法来讨论纵向数据随机缺失的变系数部分非线性分位数回归模型的估计问题.
1 估计方法
考虑如下变系数部分非线性分位数回归模型
(2)
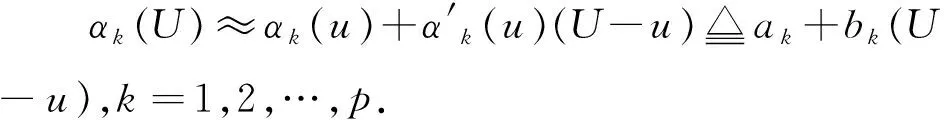
假设{Yij,Xij,Zij,Uij,i=1,…,n,j=1,…,ni}是来自模型(2)的一组随机样本,i和j表示第i个个体的第j次观测值.响应变量Yij随机缺失 (MAR),即δij=1时,Yij可以观测到;当δij=0时,Yij缺失,且满足
P(δij=1|Yij,Uij,Xij,Zij)=
P(δij=1|Uij,Xij,Zij)=π(Uij,Xij,Zij)

(3)
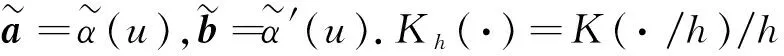
(4)
进一步有α(·)改进后的估计量
(5)
然而,在一些实际应用中,缺失概率π(Vij)一般是未知的,本文选择logistic回归模型作为缺失机制,即
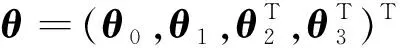
(6)
(7)
2 主要结果
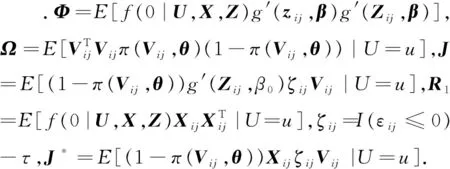
此外,给出一些证明过程中所需要的条件,如下常见的条件可参考文献[1,13].
C1 对任意的z,g(z,β)是β的连续函数,并且g(z,β)关于β的二阶连续导数.

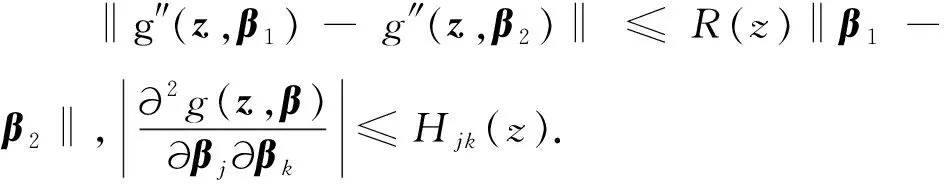
C4 随机变量U具有有界支撑Ω,其密度函数fU(·)在Ω上Lipschitz连续且大于零.
C5 变系数函数α1(·),…,αp(·)在Ω上二阶连续可导.
C6 条件密度函数f(·|X,Z,U)大于零,其导函数连续一致有界.
C7 选择概率π(u,x,z)有界且大于零,并且有连续二阶偏导数.
2.1 参数部分渐近性质
定理1 假设π(V)是已知的,在C1-C8条件下,有
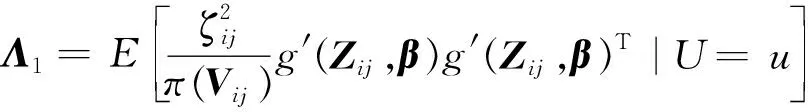
定理2 假设π(V)符合(7)且参数θ未知,在C1-C8条件下,有
其中:Λ2=Λ1-JTΩ-1J.
2.2 非参数部分渐近性质
定理3 假设π(V)是已知的,在C1-C8条件下,有
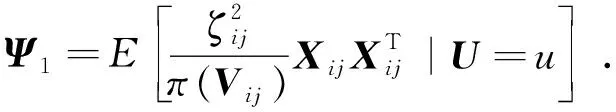
定理4 假设π(V)符合(7)且参数θ未知,在C1-C8条件下,有
其中:Ψ2=Ψ1-J*TΩ-1J*.
3 定理的证明
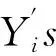
该引理证明细节可详见文献[14].

该引理证明细节可详见文献[15].
定理1的证明
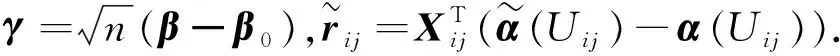
由KNIGHT[16]提出的恒等式

(8)
可得

又因为Bn(γ)-E[Bn(γ)|U,X,Z]=oP(1),所以


由Cramer-Wold理论和中心极限定理可得
最后根据Lindeberg-Feller中的极限定理有
定理1证毕.
定理2的证明
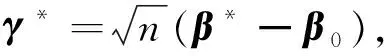
根据式(8)可得

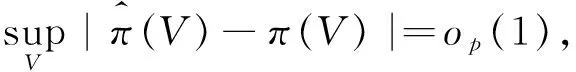
(9)
(10)
其中:π′(Vij,θ)=π(Vij,θ)(1-π(Vij,θ))Vij.根据式(9)、(10)可得

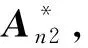
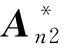

因此
定理3的证明

根据恒等式(8)有
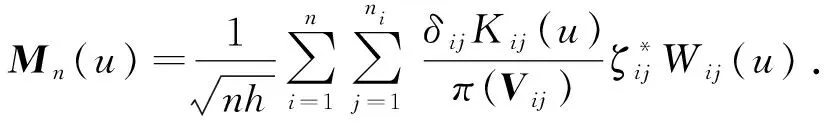
与定理1证明类似,求Nn(ξ)的条件期望,即
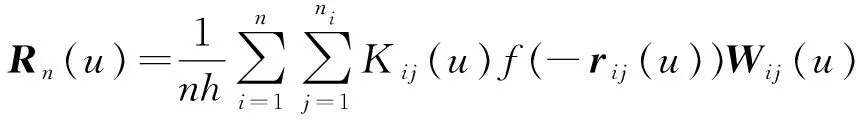
Wij(u)T.
因为E[Rn(u)]=fU(u)R(u)+O(h2),R(u)=diag(R1(u),R2(u)),
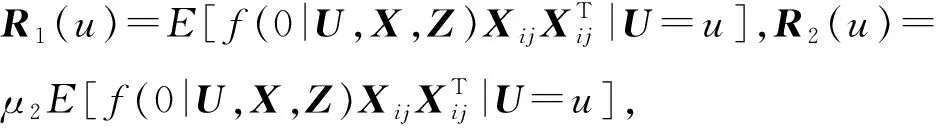
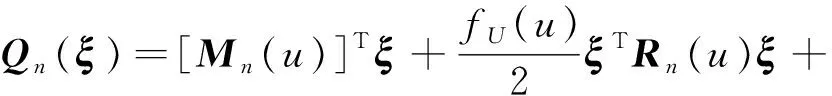
(11)
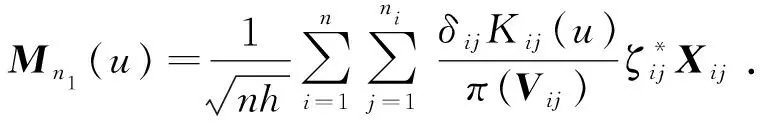
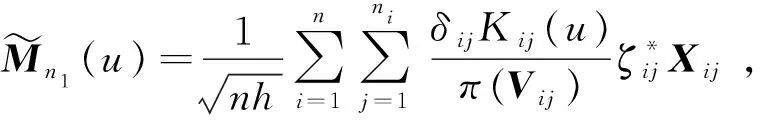
此外,与TANG[12]的定理1证明过程类似,
定理3证毕.
定理4的证明
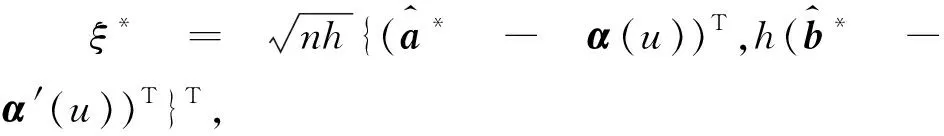
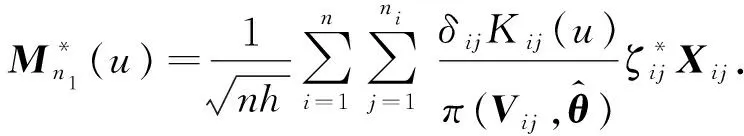
根据中心极限定理,最终有
定理4证毕.
4 数值模拟
本节过数值模拟来验证所提方法的有限样本性.考虑如下模型
i=1,…,n,j=1,…,ni,

模拟1
根据上述模型,选择如下三种选择概率函数
π1(u,x,z)=P(δ=1|U=u,X=x,Z=z)=
{1+exp(u+x+2z+4.5)}-1
π2(u,x,z)=P(δ=1|U=u,X=x,Z=z)=
{1+0.6exp(u+x+z+1.4)}-1
π3(u,x,z)=P(δ=1|U=u,X=x,Z=z)=
{1.5+exp(u-x-z-2)}-1
以上三种情形对于数据的平均缺失概率分别约为10%,30%,50%.在模拟过程中,误差服从标准正态分布, 样本容量分别取n=300,500,800,并且重复观测次数为ni=3,且对每一种情况实验重复1 000次.表1、2分别为分位数τ=0.5,0.75时参数估计量的均值(Mean),偏差(Bias),标准差(SD)和均方误差(MSE)的结果.
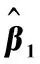
表1 τ=0.5时和的均值(Mean),偏差(Bias),标准差(SD)和均方误差(MSE)
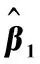
表2 τ=0.5时和的均值(Mean),偏差(Bias),标准差(SD)和均方误差(MSE)
由表1、2可以看出:
1) 当缺失概率函数和分位数一定时,随着样本量的增加,参数估计量的标准差和均方误差都在减小;
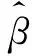
3) 当缺失概率函数和样本容量一定时,相比在τ=0.5时参数的估计效果,τ=0.75时的参数估计效果较好.
模拟2
基于上述模型,考虑在相同缺失概率大约为30%,分位数为0.75,n=800时比较2种情形下分位数回归估计的优越性,且考虑3种误差分布(N(0,1),U(0,1),C(0,1)).表3为缺失概率相同且在三种误差分布下的参数估计效果.
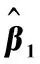
表3 缺失概率相同时和的均值(Mean),偏差(Bias),标准差(SD)和均方误差(MSE)
由表3可以看出:
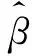
2) 当误差分布相同时,误差分布为标准正态分布的参数估计量,相比概率已知的结果,概率未知的结果较好,而其他两种误差下参数估计量的结果相差不大.
5 结 语
本文利用逆概率加权法给出了纵向数据缺失下变系数部分非线性分位数回归模型的2种参数估计,即选择概率已知、选择概率未知时的参数估计;并且在一定条件下证明了所给估计量的渐近正态性.通过数值实验说明了所得估计的有效性.
