用于训练神经网络的自适应梯度下降优化算法

阮 乐 笑

(安徽理工大学 数学与大数据学院,安徽 淮南 232001)

深度学习是一个复杂的机器学习算法,在语言和人脸识别方面[1-2]远远超过先前技术.深度学习在图像分类,医疗诊断,智能交通,音频识别领域得到广泛应用[3-6],在相关领域都取得了很多成果.深度学习让机器模仿视听和思考等人类活动,解决了很多复杂的模式识别难题,使得人工智能相关技术取得了很大进步.

最近,基于SGD优化算法已经被提出[7].AdaGrad[8]通过使用过去梯度平方和的根来控制学习率.但是在经过多次迭代之后会使得学习率非常小,从而终止了参数更新.于是AdaDelta[9]通过几个过去的梯度来解决AdaGrad的学习率递减问题.但是该算法仍然无法利用全局信息.于是有人提出了RMSProp[10],目的是将学习率除以梯度平方指数衰减平均值的根.紧接着提出了Adam,该算法主要结合了SGD和RMSprop的思想并使用了一阶矩和二阶矩.虽然Adam算法收敛速度较快,但由于不稳定和极端的学习率导致不能收敛,导致不能找到全局最优解,因此在泛化能力上不如SGD.为此提出了Adabound[11]优化算法,采用动态学习率,实现了自适应算法到SGD的平稳过渡,在保证其较高收敛速率的同时,也提高了泛化能力.diffGrad[12]通过在参数更新中使用梯度变化率引入摩擦项.RAdam[13]通过校正参数更新期间梯度的方差.Adabelief[14]通过梯度的信念计算二阶矩.同时还有一些加速算法,例如,NAdam[15]结合牛顿动量加速自适应算办法.

深度学习一般具有深层的神经网络模型结构,因此,深度模型的训练也是一项具有挑战的任务.一般情况下,衡量算法训练模型性能有两个指标:收敛速度和泛化能力.目前,应用较广泛的训练算法是随机梯度下降算法(SGD)和学习率自适应的随机梯度下降算法(Adam).其中SGD具有良好的泛化能力,但收敛速度较慢.Adam具有良好的收敛速度,但可能会因为极端学习率导致不能收敛或无法收敛到全局最优,所以泛化能力不如SGD.这就意味着Adam在学习率设计上还需要进一步提高.为此,Adam很多变体都被提出,但是最经典的还是Adabound,该算法采用了动态学习速率边界,在保证较高学习率的同时也保证了强泛化能力.

1 Adaboundinject算法设计

1.1 Adabound算法

本文介绍Adam[16]优化方法的一个变体.目的是结合自适应方法的特点,它类似于早期训练中的自适应方法和训练结束时的SGD.针对这一问题,一些人提出通过Amsgrad来解决.然而,Amsgrad的学习率低于Adam,被认为可能是学习率过高所导致.因此,推测Adam的学习率太高或太低,都会导致算法性能不佳,极端的学习率会产生不利影响.受梯度裁剪的启发,本文在Adam中使用了学习率裁剪.具体操作如下.

(1)

剪裁后控制学习率

[ηl(t),ηu(t)]

随着深度学习网络越来越复杂,模型的训练也会越来越困难,本文提出了新的优化算法Adaboundinject,在Adabound中短期的参数更新作为权重加入二阶矩中再注入一阶矩.可以更好地控制参数的更新,避免了在最小值附近振荡和无法到达全局最优值的现象,提高了Adabound的性能.

1.2 Adaboundinject算法

本文提出了新的自适应优化算法,在优化过程中,将二阶矩注入一阶矩中,其计算方法如下:

(2)

其中:Δθ=θt-2-θt-1,为短期的参数更新,k为注入的超参数,在接近最小值时,执行较小的参数更新,更好地接近最小值,避免了局部最优.具体的算法设计如下.

2 收敛性分析

2.1 简介

我们可以将在线凸优化视为一种迭代游戏.在第K轮中,决策者会做出决策,但在做出决策之前不知道结果.在做出决定后,决策者会知道自己遭受了多少损失.这种损失可以被视为在线凸优化过程中正确答案和决策结果之间的差距.决策集是n维欧氏空间K⊆Rn中的一个凸集.损失可以看作是定义在凸集K上的有界凸函数.然后,可以将此问题视为一个优化问题.即学习者xt在做出决策时产生的最小成本ft(xt),即

通常将T轮迭代博弈中决策者的总成本[17]和最优成本之间的差定义为算法的遗憾界.经过T次迭代后,可以通过以下公式表示遗憾

2.2 遗憾分析

证明：由文献[16]中引理10.2有

接下来,用提出的Adabound注入更新公式

则

将上面的更新公式进行重新排列

由文献[16]中引理 10.4,对ft(xt)-ft(x*)在i∈1,…,d的上界在t=1,…,T的累加求和,得出遗憾界满足

对上式进行放缩:

对定理1中参数设置和条件,有

证明：利用L2范数的定义

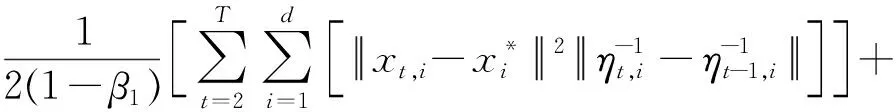
对定理1中参数设置和条件,有

证明：定义ηt,有

因此

对定理1的参数设置和条件,有

证明：

所以

所以,遗憾界可以进一步表示为:

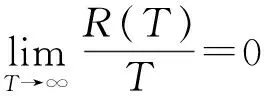
3 深度神经网络实验

卷积神经网络的目标函数是非凸的,尤其是多层卷积.在非凸形环境下.本文选择ResNet、VGG和SENet深度神经网络进行实验,并采用CIFAR数据集作为训练模型.

3.1 ResNet-18,VGG-16和SENet-18在CIFAR-10上的图像分类

在图像分类任务中,本文选择使用CIFAR-10数据集来测试深度神经网络ResNet-18[18],VGG-16[19]和SENet-18[20].CIFAR-10[21]是一个用于识别常见对象的小型数据集.共包括十类彩色图片,图片大小为32×32.该数据集包含50 000张训练图片和10 000张测试图片.在实验中比较了在不同的网络下Adaboundinject算法和其他自适应算法的性能.从图1中可以清楚地看出,Adaboundinject算法的精确度都高于其他算法,也比其他算法更稳定.同时,在表1中可以看出该算法的损失也是最少的.

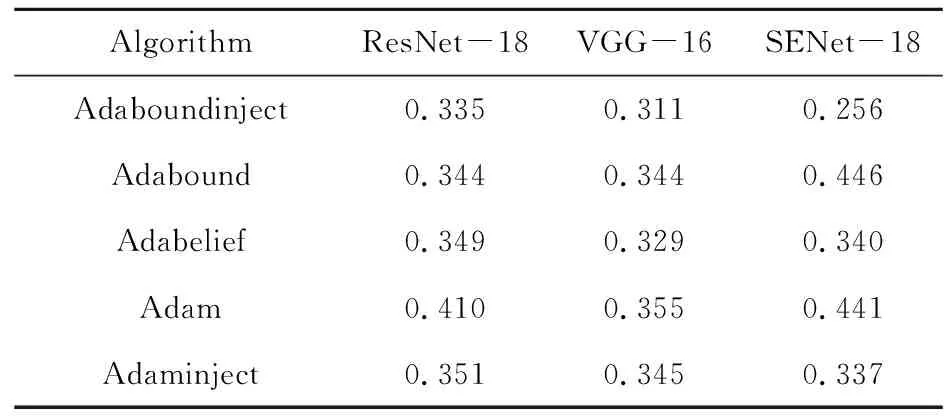
表1 ResNet-18,VGG-16和SENet-18在CIFAR-10测试集上的损失Table 1 Test loss for ResNet-18, VGG-16 and SENet-18 on CIFAR-10

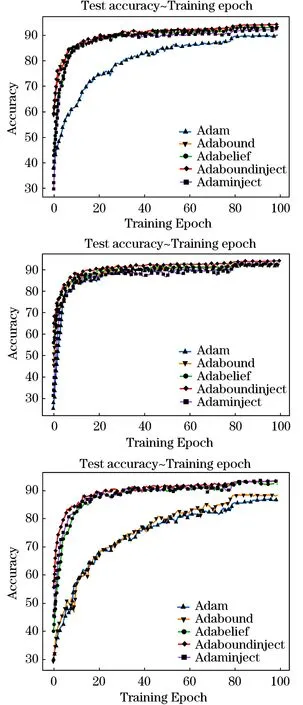
图1 ResNet-18,VGG-16和SENet-18在CIFAR-10测试集上的精确度Figure 1 Test accuracy for ResNet-18, VGG-16 and SENet-18 on CIFAR-10

3.2 ResNet-18,VGG-16和SENet-18在CIFAR-100上的图像分类

在图像分类任务中,选择使用CIFAR-100数据集来测试深度神经网络ResNet-18,VGG-16和SENet-18.CIFAR-100数据集是一种用于机器视觉领域的图像分类数据集.共有100个类别.每个类别有600张尺寸为的彩色图像,其中500张用作训练集,100张用作测试集.从图2中可以清楚地看出,在不同网络下,该算法在测试集上,精确度都比其他算法更高,同时在表2中也可以看出,该算法的损失最低.进一步说明本文算法具有更好的性能.

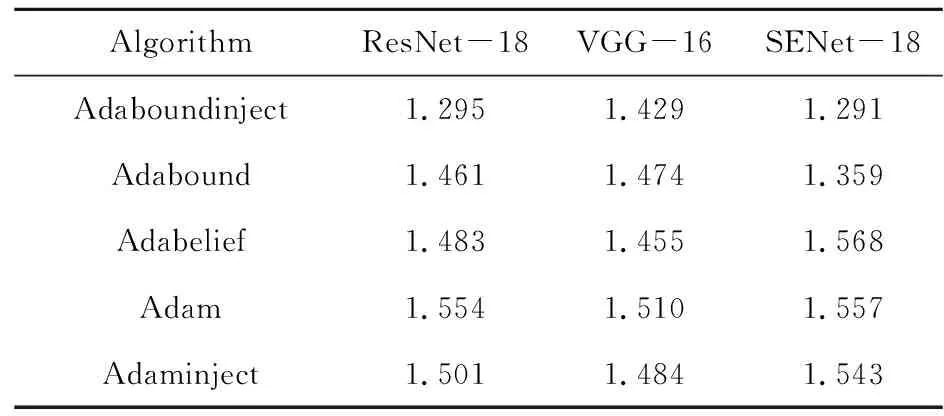
表2 ResNet-18,VGG-16和SENet-18在CIFAR-100测试集上的损失Table2 Test loss for ResNet-18, VGG-16 and SENet-18 on CIFAR-100

图2 ResNet-18,VGG-16和SENet-18在CIFAR-100测试集上的精确度Figure 2 Test accuracy for ResNet-18, VGG-16 and SENet-18 on CIFAR-100

3.3 ResNet-18,VGG-16和SENet-18在FashionMNIST上的图像分类

在图像分类任务中,本文选择使用FashionMNIST数据集来测试深度神经网络ResNet-18,VGG-16和SENet-18.FashionMNIST数据集包含70 000张灰度图像,其中包含60,000个示例的训练集和10,000个[22]示例的测试集,每个类别都是一个 灰度图像.表3展示了经过100次迭代之后,使用不同优化器训练不同的深度神经网络在FashionMNIST测试集上的精确度,通过数据可以看出,本文算法优于其他算法.

表3 ResNet-18,VGG-16和SENet-18在FashionMNIST测试集上的精确度Table 3 Test accuracy for ResNet-18, VGG-16 and SENet-18 on FashionMNIST

4 结 语

本文提出了Adaboundinject算法,该算法通过将Adabound算法二阶矩注入一阶矩得到.Adaboundinject具有良好的泛化能力和较快的收敛速度.同时在凸设置下证明了该算法的收敛性,在非凸设置下,通过实验对比可以直观地观察到Adaboundinject具有更好的性能.在图像分割的三个数据集下都证实了将二阶矩注入一阶矩可以提高Adabound的性能,与其他典型的优化算法相比,Adaboundinject性能更好.

目前的工作中将二阶矩注入一阶矩中可以更好的接近最优值.本文证明是在常见的假设下完成,所提出的算法在应用方面可能会受到限制.因此,下一步将探索把算法拓展到更广义的条件下进行改进.