隧道开挖对上覆既有管线影响的简化解析计算方法*

董瑞桥 施展斌

(1.中铁十八局集团有限公司,300222,天津; 2.浙江大学滨海和城市岩土工程研究中心,310058,杭州)

由于城市轨道交通的快速发展,新建隧道开挖对邻近既有隧道或管线会产生较大的不利影响。目前,大多数研究通过两阶段分析法对其进行计算,并推导理论解析计算方法。第一阶段可以采用文献[1]提出的Longanathan解析法获得周边土体在隧道开挖下的自由位移场,第二阶段将既有管线简化为搁置在Winkler或Pasternak地基模型上的梁,并建立该状态下的管线受力平衡控制方程,从而获得既有管线相应的地变形响应。文献[2]提出考虑土体剪切变形的Pasternak和Vlazov双参数地基模型。文献[3-4]将管线简化为Euler-Bernoulli梁和Timoshenko梁搁置在Pasternak地基模型上,获得了邻近隧道开挖引起的既有管线变形响应。此外,文献[5-8]的研究表明,三参数Kerr地基模型对于预测土同隧道及桩基间的相互作用较为准确,但由于其参数较多,公式较为复杂,难以在实际工程中应用。

由此可知,考虑管线侧向土体作用对既有管线受力变形的影响研究较少。基于此,本文基于两阶段法提出了一种可预测隧道开挖对上覆既有管线变形响应影响的简化计算方法,将既有管线假定成搁置在Vlazov地基模型上的Euler-Bernoulli梁,引入侧向土体的影响,进一步获得了盾构开挖引起上覆既有管线变形的解析计算方法。此外,本文系统地分析了地层损失率、隧道开挖半径、新建隧道与既有管线夹角变化对既有管线受力变形的影响。

1 理论分析方法

Vlazov地基模型示意图见图1。既有管线被假定为搁置在Vlazov地基模型上的Euler-Bernoulli梁,管线受到的附加荷载为q(单位为N)。

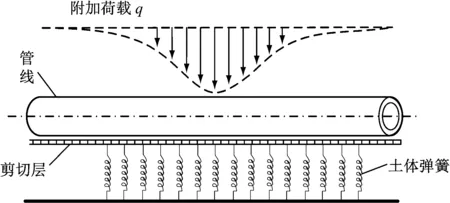
图1 Vlazov地基模型示意图

根据Vlazov地基模型及管线侧向土体影响[9],可以进一步推导获得管线沉降变形的控制方程:

(1)

式中:

w——管线沉降值;

J——管线抗弯刚度;

D——管线直径;

K——地基弹簧刚度;

t——地基切应力;

x——沿着既有管线中线水平方向的坐标值。

式(1)为4阶微分方程,可采用差分法进行求解,考虑到实际管线两端边界受到隧道开挖的影响很小,可将两端简化为两个自由端[5,7-8],则式(1)可简化为:

w(K1+K2-G0)=qD

(2)

式中:

K1——管线单元刚度矩阵;

K2——地基刚度矩阵;

G0——地基剪切刚度矩阵;

w——管线沉降矩阵;

q——管线附加应力列向量。

具体矩阵求解方法可参考文献[5-9]。此时,可得到管线沉降的解析解,由材料力学理论可进一步获得管线的弯矩和剪力。值得注意的是,当不考虑侧向土体力时,可获得退化的双参数Vlazov地基解(以下简称“EB-V法”);当不考虑侧向力及土体剪切效应时,可获得退化的Winkler地基解 (以下简称“EB-W法”)。

2 算例验证

2.1 工程概况

深圳某地铁隧道垂直下穿既有管线模型示意图如图2所示。根据文献[10]的研究可知,隧道开挖引起的地层损失率ε=0.84%,管线和隧道埋深分别为8.7 m和14.4 m,两者的半径分别为1.5 m和3.0 m,土体弹性模量和泊松比分别为8.2 MPa和5.87×1010。

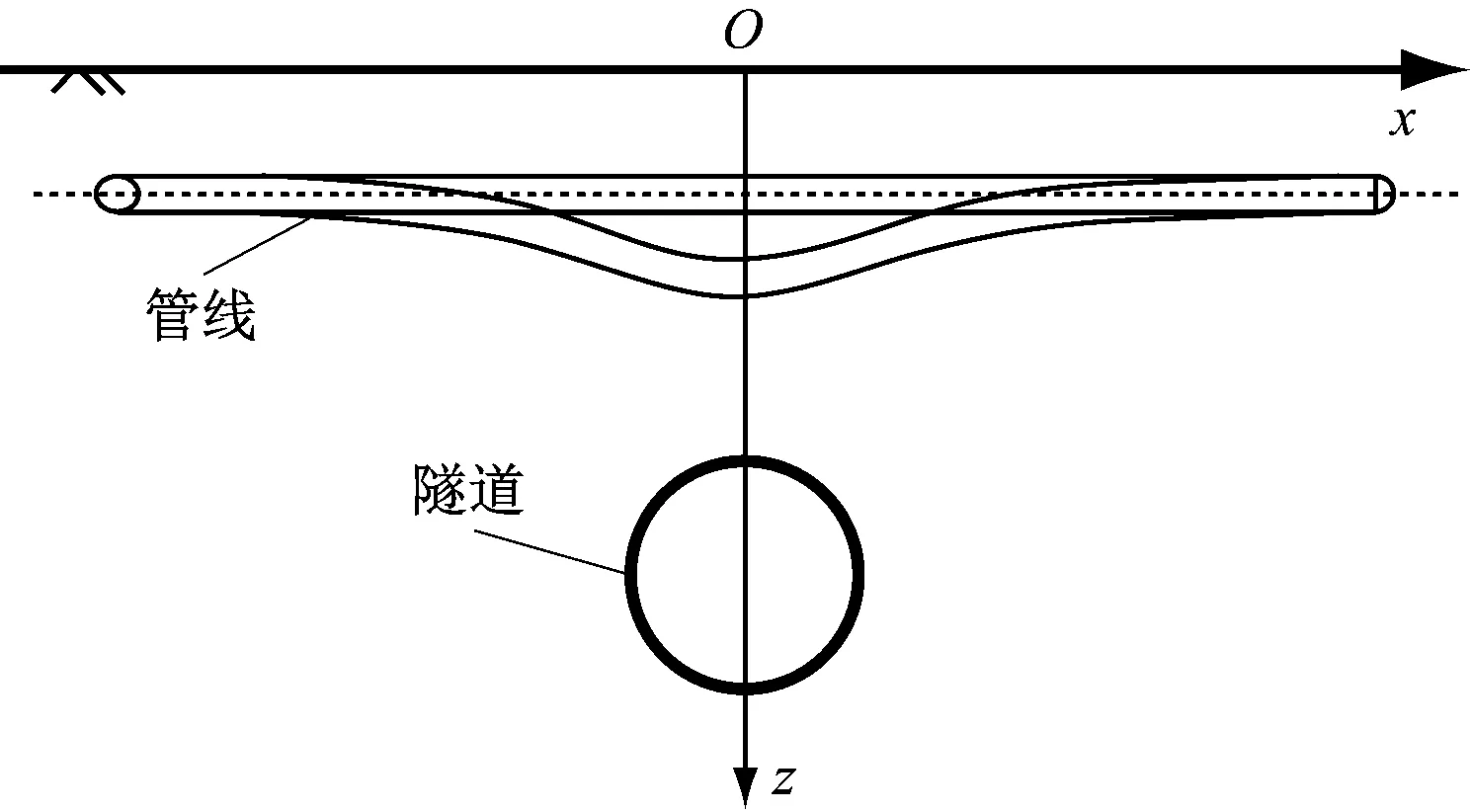
图2 深圳某地铁隧道垂直下穿既有管线模型示意图

2.2 计算结果分析

将不同计算方法所得既有管线竖向位移与文献[10]的实测数据进行对比,如图3所示。由图3可知:既有管线发生大变形范围集中在隧道中轴线两侧30 m范围内,所提简化计算方法、EB-V法和EB-W法所得结果均较为符合实测数据的分布;采用所提简化计算方法获得的管线最大沉降为7.6 mm;EB-V法的计算结果较小,其最大沉降值为5.9 mm;EB-W法的计算结果明显偏大,管线最大沉降值为10.9 mm。造成这一现象的原因在于EB-W模型忽略了既有管线侧向土体对管-土相互作用的影响,导致其预测结果低估了下穿隧道对既有管线的影响。与EB-V法和EB-W法相比较,文献[10]中实测数据的管线最大沉降为8.0 mm,与本文所提简化计算方法的计算结果更为相符。

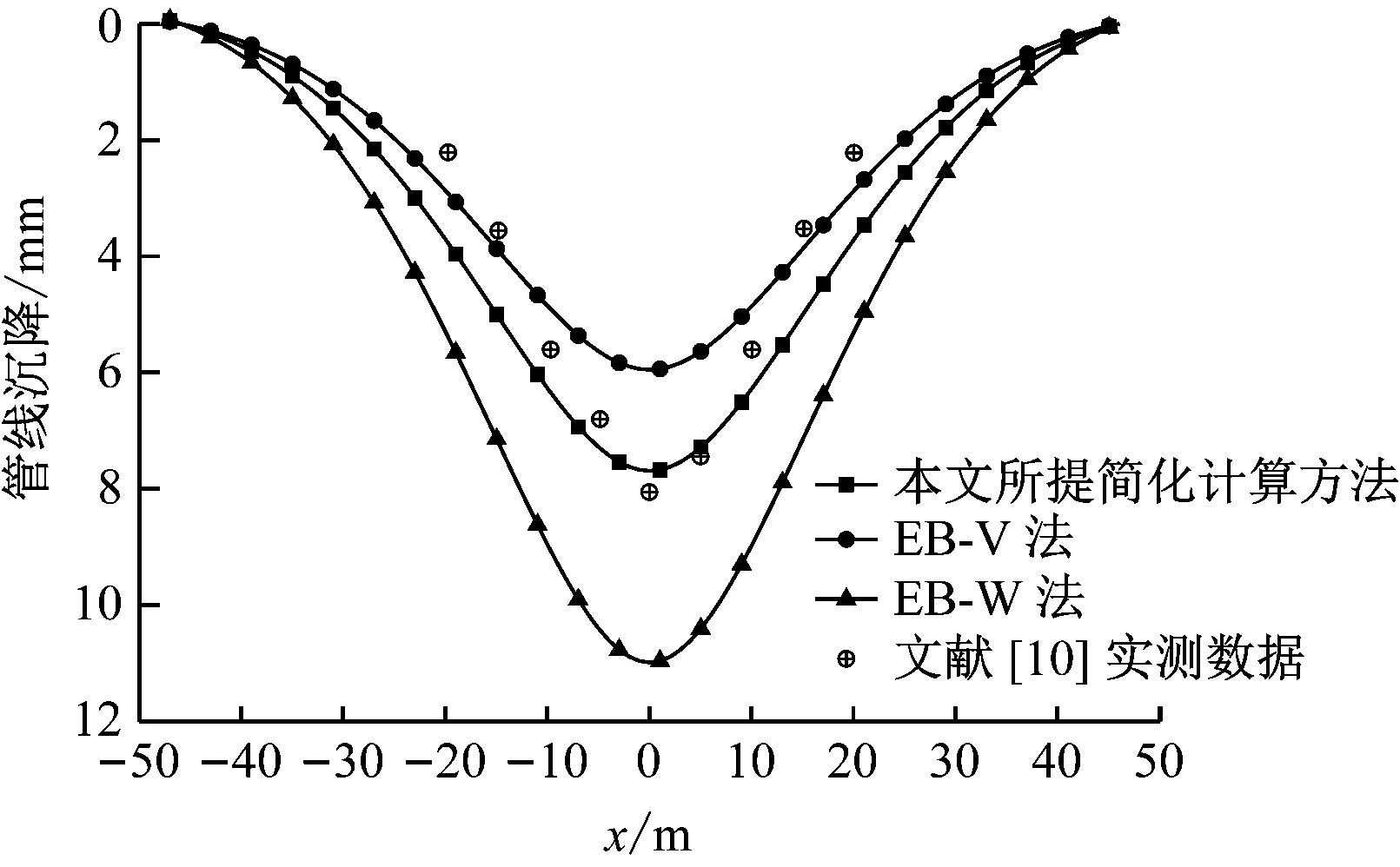
注:x以管线中线向右为正,以管线中线向左为负;余类同。

不同计算方法下,管线弯矩同管线上的点与管线中线水平距离间的关系如图4所示。由图4可知:本文所提简化计算方法与EB-V法的计算结果较为相近,但本文所提简化计算方法的计算结果偏大;EB-W法的计算结果明显更大。因此,本文所提简化计算方法及EB-V法在预测管-土相互作用时有较大的优势,进一步验证了本文所提简化计算方法的合理性。

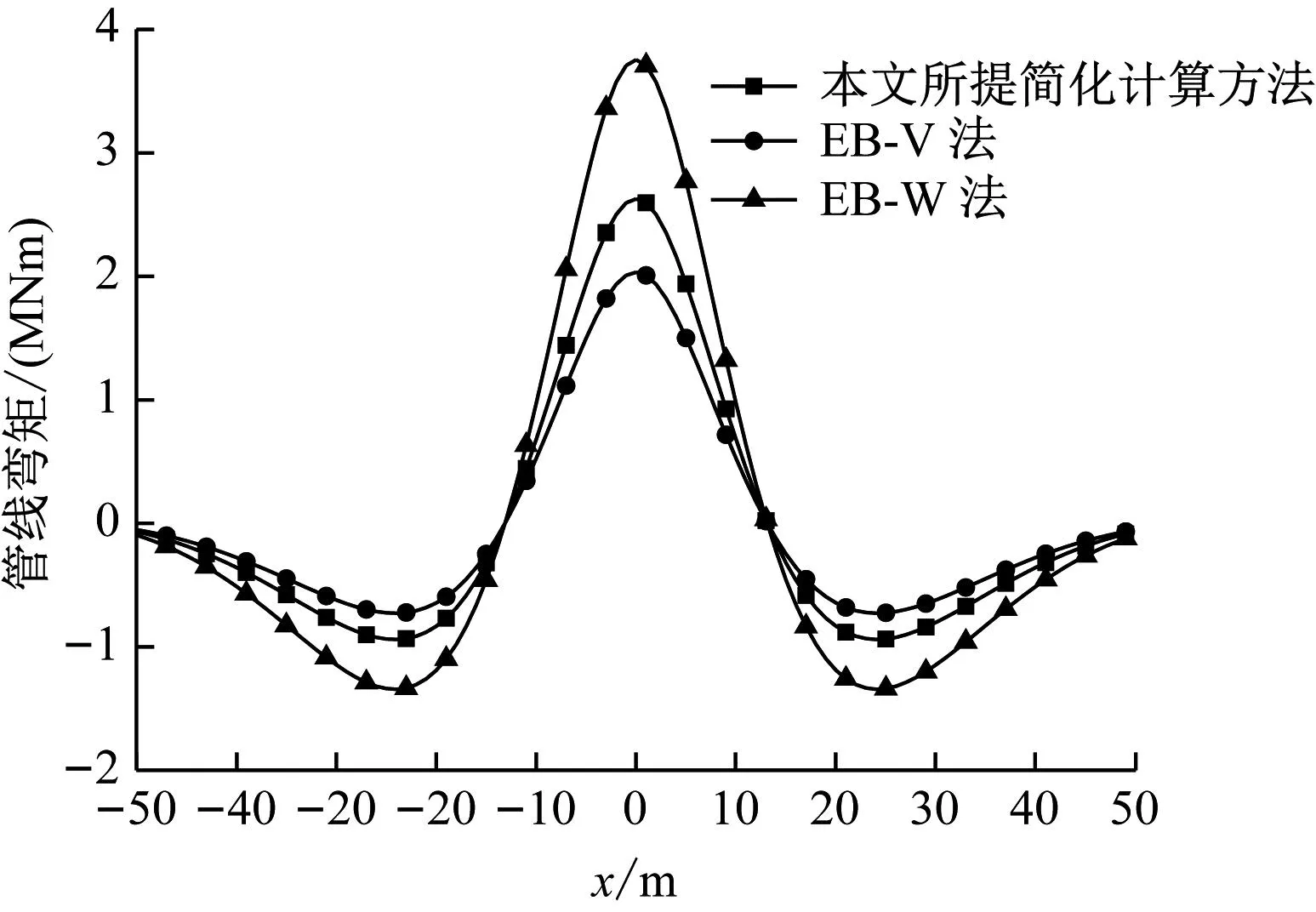
注:弯矩以管线下侧受拉为正,以管线上侧受拉为负;余类同。

3 敏感参数分析

考虑到地层损失率、隧道开挖半径及新建隧道与管线夹角θ的变化对上覆既有管线受力变形响应的影响,假设隧道轴线和管线轴线垂直相交,管线和隧道埋深分别为10 m和18 m,两者半径分别为1.5 m和3.0 m,土体弹性模量和泊松比分别为10 MPa和5.87×1010。

3.1 地层损失率

不同地层损失率下,管线的沉降及弯矩随管线上的点与管线中线水平距离的变化情况,如图5所示。既有管线沉降变形和弯矩变化曲线沿管线中心轴线对称分布,且管线纵向最大沉降和最大弯矩值均出现在管线中心轴处。同时,既有管线纵向沉降及弯矩随着地层损失率的增大而线性增大。这是由于管线附加应力随着地层损失率线性增大,致使既有管线每个位置处的沉降也随着地层损失率线性变化。因此在实际工程中,应尽可能减小盾构造成的地层损失率,以减轻对邻近建筑物的损害。

a) 管线沉降

3.2 隧道开挖半径

不同隧道开挖半径下,管线的最大沉降和最大弯矩如图6所示。由图6可知:随着隧道开挖半径从3.0 m增加至5.5 m过程中,既有管线最大沉降从4.4 mm逐渐增大至15.5 mm,增幅高达2.5倍,且增长速率有逐渐增大的趋势;随着隧道开挖半径的增大,管线最大弯矩从1.4 MNm逐渐增大至4.7 MNm,弯矩增幅接近2.36倍。这说明增大隧道开挖半径对上覆既有管线影响较大,且管线应力应变峰值增速会越来越快,故在实际工程中,应尽可能减小隧道开挖半径以降低地层应力变化对上覆既有管线的影响。

图6 不同隧道开挖半径下管线的最大沉降和最大弯矩

3.3 新建隧道与既有管线夹角

不同新建隧道与既有管线夹角下,管线的最大沉降和最大弯矩如图7所示。由图7可知:新建隧道与既有管线夹角从15°增大至90°过程中,既有管线最大纵向沉降从8.1 mm逐渐减小至4.4 mm,降幅约为46%,其减小速率逐渐平缓;随着新建隧道与既有管线夹角的增大,管线最大弯矩从0.52 MNm逐渐增大至1.41 MNm,弯矩增幅接近1.7倍,其增长速率也逐渐平缓。这说明新建隧道与既有管线夹角是引起上覆既有管线沉降及其内力变化的敏感参数,在实际工程中应注意新建隧道和既有管线夹角的变化对既有管线变形受力的影响。

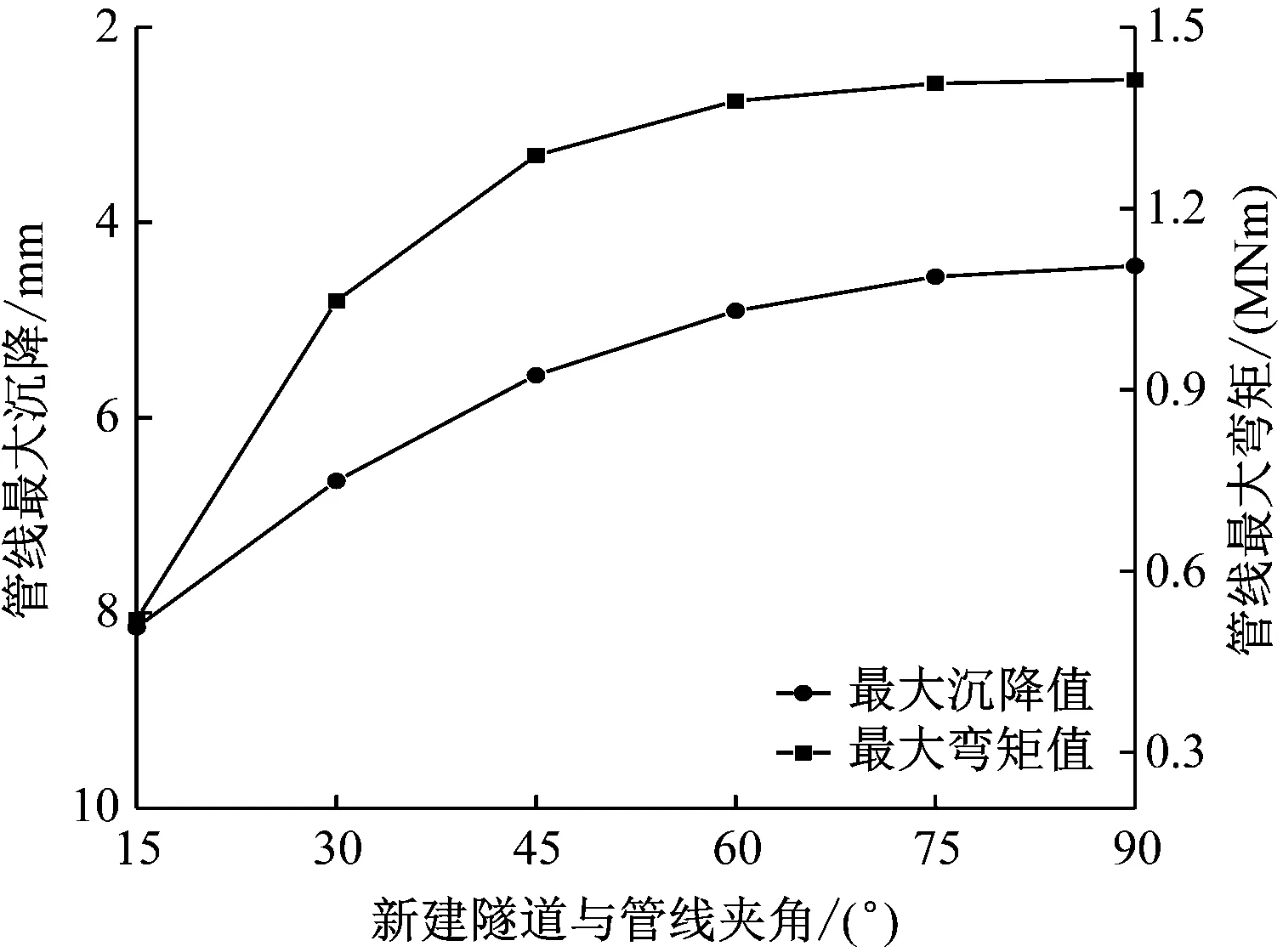
图7 不同新建隧道与既有管线夹角下管线的最大沉降和最大弯矩

4 结语

本文基于两阶段法提出了一种可预测隧道开挖对上覆既有管线变形响应影响的简化计算方法,主要获得以下几个结论:

1) 将管线假定成搁置在Vlazov地基模型上的Euler-Bernoulli梁,引入了管线两侧侧向土体的影响,采用有限差分法简化获得管线受力变形响应。

2) 与深圳地铁某地铁隧道实测数据进行对比,本文所提简化计算方法结果与实测数据基本吻合,更接近实测数据。

3) 增大地层损失率能够有效增大既有管线的沉降及其内力;管线的沉降及弯矩值随着下穿隧道开挖半径的增大而逐渐增大;增大新建隧道与既有管线的夹角会引起管线沉降的减小,但会增大管线的内力。