基于Adaline算法的高速磁浮列车谐波检测及抑制方法
2024-02-22毛中亚李凌霄王宗艳
毛中亚 王 勇 李凌霄 王宗艳
(同济大学电子与信息工程学院,201804,上海)
近年来,我国高速磁浮技术获得了快速发展,尤其是运行速度为600 km/h的高速磁浮列车的示范运营,标志着其技术水平已进入到世界领先水平。高速磁浮列车牵引供电系统采用直流电流供给同步直线电机和各种车载设备用电,直流电流主要通过多重整流器整流交流电流后获得。在这个过程中,多重整流器的开关动作会产生较多高次谐波,进而导致电流畸变[1-2],而这些畸变电流会降低高速磁浮列车系统的安全性和可靠性,同时也会造成电网电能质量的下降。
目前,神经网络因其简单性、学习能力和强泛化能力受到了研究者们的关注,已被应用于谐波检测领域。神经网络具有自适应能力和学习能力,通过训练可以自行处理数据,自动发现研究对象的规律和特点。应用神经网络的目的是利用特定的函数和网络结构来训练神经网络的权值和参数,使目标输出及均方误差最小。利用神经网络对高速磁浮谐波进行有效检测,并采取适当的控制策略产生相应的补偿电流对谐波进行抑制,减少电网电流的畸变。
本文针对高速磁浮列车牵引供电系统中存在的谐波问题,通过构建基于Adaline神经网络算法的高速磁浮谐波检测模型,采用谐波补偿控制策略,进行了谐波检测及抑制的仿真研究。研究结果表明,所提谐波检测及抑制方法可以有效减少系统中的谐波畸变率,改善电流波形品质,提高电能质量。本文研究可为高速磁浮列车的安全稳定运行提供一种有效的谐波抑制策略,具有一定的工程应用价值。
1 高速磁浮列车牵引供电系统谐波分析
1.1 牵引供电系统
以上海磁浮列车示范运营线的牵引供电系统为例进行分析,其主要由四部分组成:①同步直线电机,即电能动能转换装置;②逆变器,其是采用PWM(脉冲宽度调制)控制的GTO(门控晶闸管)逆变器;③直流联结电路;④整流器,其是采用双三相半控12脉冲的多重整流装置[3-4]。牵引供电系统产生可变电压和可变频率信号,为同步直线电机提供动力,进而驱动列车运行。高速磁浮列车牵引供电系统框图如图1所示。
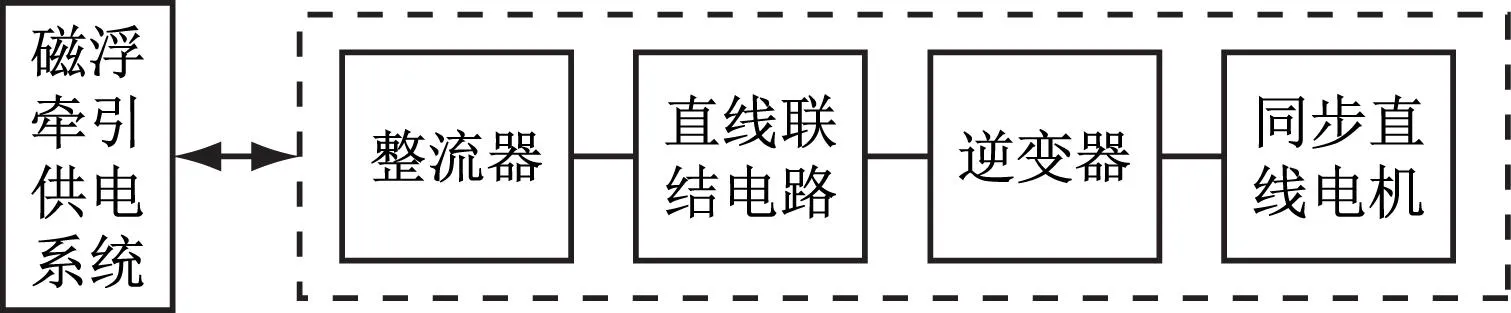
图1 高速磁浮列车牵引供电系统框图
牵引供电系统产生谐波电流的原因有:①在整流器切换过程中,有谐波电流注入供电系统;②逆变器作用。由于大部分逆变器谐波在进入电源侧前已被直流母线电路滤除,逆变器产生的谐波相对较弱,其影响可以忽略不计。因此,本文所提谐波抑制方法主要针对多重整流器运行时产生的谐波。
1.2 多重整流电路

网侧整流变压器一次侧输入端电流Ia可以表示为:
(1)
式中:
Id——整流器输出电流;
n——谐波次数,n=12k±1;
k——正整数;
t——时间;
ω——市电电网角频率。
由式(1)可知,双三相半控12脉冲多重整流电路的Ia主要有12k±1次谐波,即高速磁浮畸变电流中的主要谐波为11、13、23、25、35、37次等高次谐波。
2 基于Adaline算法的高速磁浮谐波检测
根据前文的谐波分析,对式(1)进行改写:
Ia=w1sinωt+w2sin 11ωt+w3sin 13ωt+
w4sin 23ωt+w5sin 25ωt+w6sin 35ωt+
w7sin 37ωt+w8cosωt+w9cos 11ωt+
w10cos 13ωt+w11cos 23ωt+w12cos 25ωt+
w13cos 35ωt+w14cos 37ωt
(2)
式中:
w1,w2,…,w14——基波和各次谐波的权值。
定义矩阵W、S、C分别为基波和各高次谐波的权值矩阵、正弦谐波矩阵和余弦谐波矩阵,则式(2)中的函数关系可以表示为:
W=[w1w2…w13w14]
(3)
S=[s1s2s3s4s5s6s7]T=[sinωtsin 11ωtsin 13ωtsin 23ωtsin 25ωtsin 35ωtsin 37ωt]T
(4)
C=[c1c2c3c4c5c6c7]T=[cosωtcos 11ωtcos 13ωtcos 23ωtcos 25ωtcos 35ωtcos 37ωt]T
(5)
(6)
式中:
si——基波(i=1)和高次谐波(i≠1)的正弦波分量;
wi——基波(i=1)和高次谐波(i≠1)正弦波分量的权值;
wj——基波(j=1)和高次谐波(j≠1)余弦波分量的权值;
cj——基波(j=1)和高次谐波(j≠1)的余弦波分量。
由式(3)—式(6)可以构造Adaline神经网络谐波检测模型,其示意图如图2所示。

注:I1为畸变电流的基波成分;Ih为畸变电流中的高次谐波成分;为神经网络检测出来的畸变电流中的基波成分;为神经网络检测出来的畸变电流中的高次谐波成分;e为误差函数。
Adaline神经网络使用梯度下降法来更新权值,使得代价函数J最小化[5-6]。根据梯度下降法的更新规则[7],可以通过式(7)来更新权值:
wt+1=wt-η∂J/∂wt
(7)
式中:
wt——t时刻各次谐波的权值;
η——学习速率,且0<η<1。
根据图2所示的Adaline神经网络谐波检测模型,除去基波后,畸变电流中的高次谐波成分为:
(8)
利用基于Adaline算法的谐波检测模块检测出高次谐波分量,然后在谐波补偿控制模块采用一定的补偿控制策略对谐波进行抑制。所采用的补偿控制策略是根据检测出的谐波情况,将其转化为与其方向相反、大小相等的电流,并作为补偿信号馈入牵引供电网。这种基于Adaline算法的谐波检测及抑制方法,可以抵消牵引供电系统中的高次谐波信号,有效抑制牵引供电系统中的谐波信号,达到对牵引供电系统电流信号进行谐波抑制的目的。
3 基于Adaline算法的谐波检测及抑制仿真
3.1 多重整流电路仿真
把两个半控12脉冲多重整流电路并联连接,再接入三相电压,并在直流输出处接上阻感负载,即可模拟高速磁浮系统的24脉冲多重整流电路模块。根据高速磁浮牵引系统多重整流电路原理,在MATLAB/Simulink软件中对24脉冲多重整流电路进行仿真。高速磁浮多重整流电路仿真图如图3所示。仿真后得到的输出端电压、输入端三相电流及谐波FFT(快速傅里叶变换)仿真波形如图4所示。
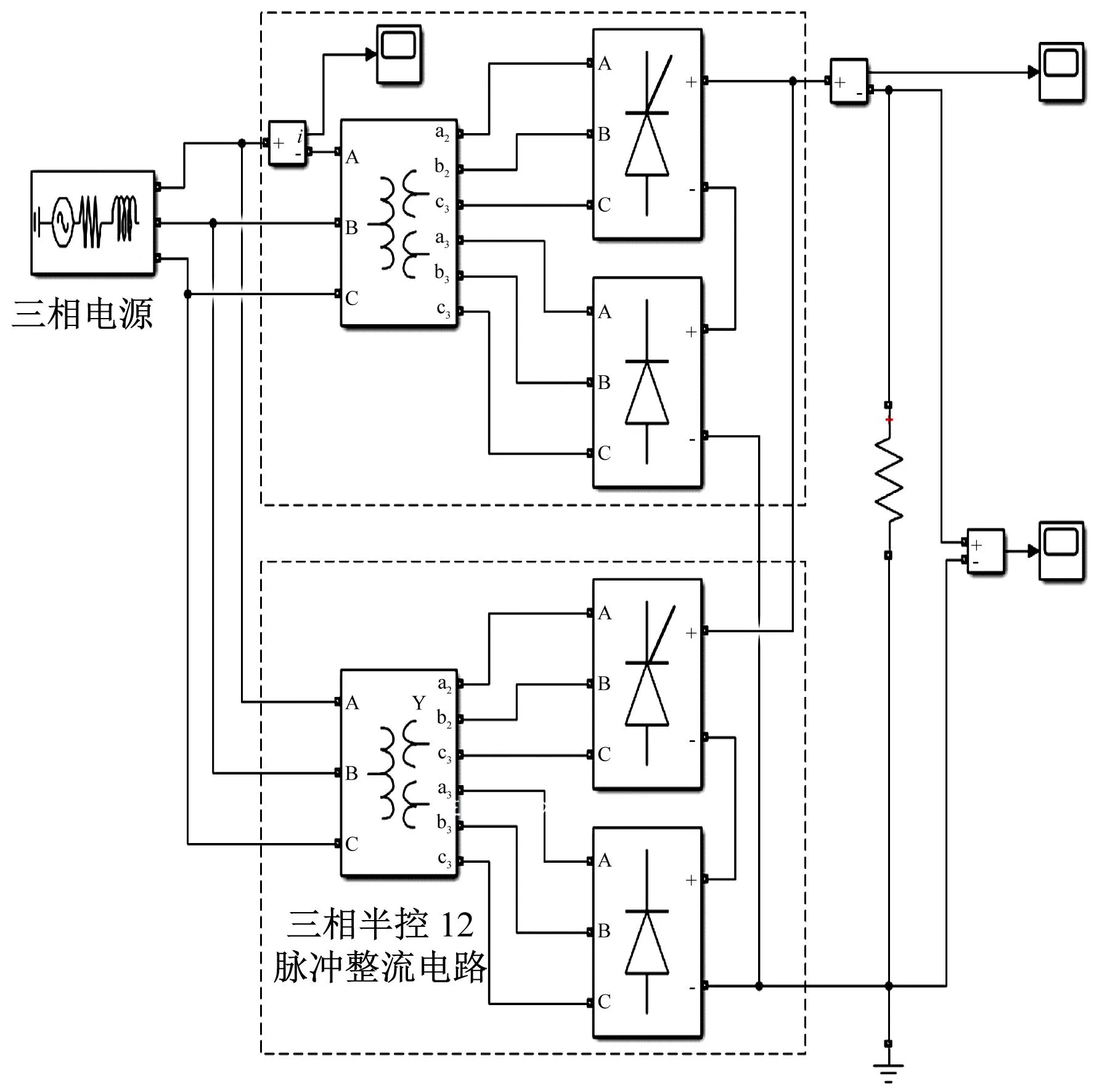
注:A、B、C为输入电流端;a2、b2、c2、a3、b3、c3为输出电流端。
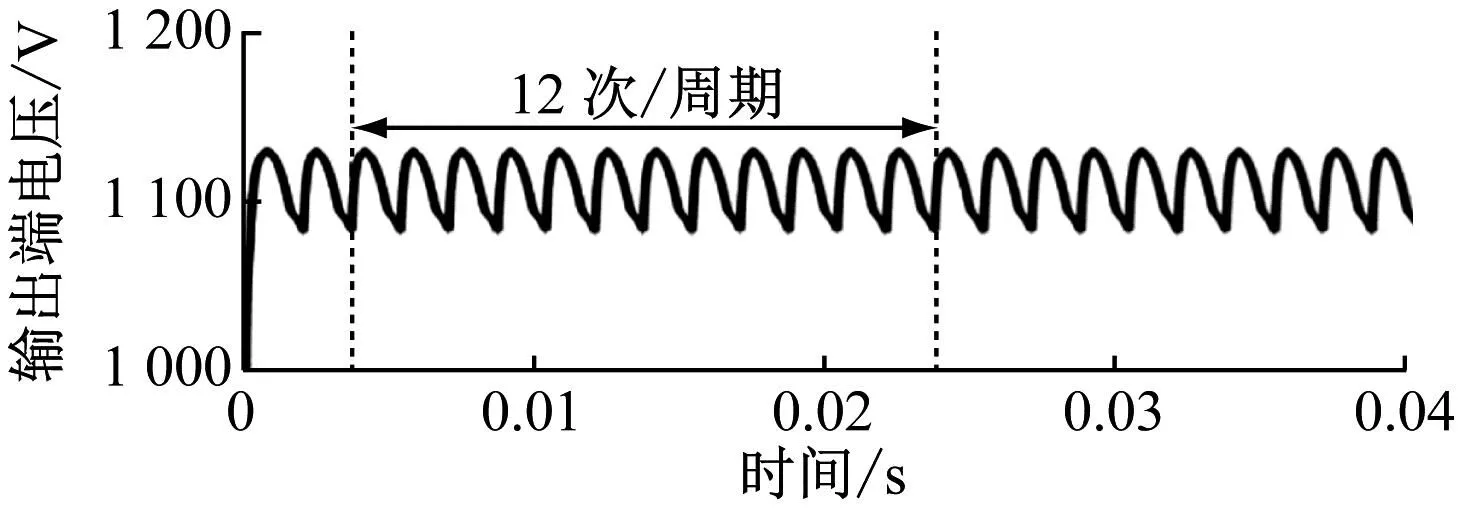
a) 输出端电压波形
输出端电压波形一周期脉动次数为12次,这是由于该模型采用的是双三相12脉冲整流电路并联连接,其特性与12脉冲多重整流电路的特性相似。对输入端三相电流波形进行FFT分析,可以获得双三相12脉冲多重整流电路谐波成分及谐波畸变率。畸变电流中的主要谐波次数为11、13、23、25、35、37次,这些高次谐波幅值在基波幅值中的占比分别为8.727%、5.633%、2.987%、2.161%、1.161%、0.858%,谐波畸变率为11.16%。
3.2 谐波检测与抑制仿真
为验证所提基于Adaline算法的高速磁浮谐波检测及抑制方法的准确性,基于高速磁浮牵引供电系统多重整流电路原理和Adaline神经网络谐波检测原理,在MATLAB/Simulink软件中建立了检测及抑制谐波的仿真模型,其软件截图如图5所示。其中:高速磁浮模块主要用于产生谐波并馈入到牵引网中;Adaline谐波检测模块是基于Adaline神经网络原理和Adaline神经网络谐波检测模型搭建的,主要用于检测牵引供电系统的谐波;谐波补偿控制模块主要根据Adaline谐波检测模块检测出的谐波情况,采取相应的谐波补偿控制策略并产生补偿信号,以实现对牵引供电系统中谐波的抑制。

图5 谐波检测与抑制仿真图软件截图
基于Adaline算法的高速磁浮谐波检测及抑制方法,首先经过Adaline谐波检测模块检测谐波,然后根据谐波情况,由谐波补偿控制模块产生补偿电流,对牵引供电系统进行谐波抑制。采用高速磁浮谐波检测和抑制方法后的谐波仿真波形如图6所示。由图6可知,该电路中的11、13、23、25、35、37次的谐波幅值在基波幅值中的占比分别为0.370%、0.287%、0.201%、0.168%、0.127%、0.076%,谐波畸变率为1.41%。

a) 输入端三相电流波形
综上所述,采用高速磁浮谐波检测及抑制方法可以明显改善牵引供电系统中的网侧电流波形,减少各次谐波含量,降低谐波畸变率。此外,采用高速磁浮谐波检测及抑制方法后,网侧电流的各次谐波含量均有较大幅度的降低,谐波畸变率从11.16%降至1.41%。由此可知,所提方法可以有效减少谐波畸变,提高牵引供电系统的稳定性和工作效率。
4 结语
对双三相半控12脉冲多重整流电路及其谐波进行了理论和仿真分析,高速磁浮畸变电流中的主要谐波为11、13、23、25、35、37次等12k±1次谐波,其谐波含量较高且畸变率严重。为补偿上述谐波带来的影响,采用基于Adaline算法的谐波检测及抑制方法。利用Adaline算法检测出畸变电流中的高次谐波分量,然后根据检测结果产生与高次谐波方向相反、大小相等的电流,并将其作为补偿信号馈入牵引供电网,对其进行谐波抑制。仿真结果表明,所提方法可以大大降低系统谐波畸变率,在谐波抑制方面取得了较好的效果。本文研究仅论证了离线的MATLAB软件仿真方法的理论效果,建议后续研究进一步开展试验验证。
