基于内容结构化的初中数学学业水平考试命题实践——以2023年浙江省金华卷第24题为例

傅瑞琦

(金华市教育教学研究中心,浙江 金华 321000)

《义务教育数学课程标准(2022年版)》(以下简称《课标》)在学业质量标准中提出,初中学业水平考试(以下简称“中考”)数学试题命制要选择学生熟悉、符合学生认知发展规律的数学情境,以结构化的数学知识主题为载体,评估学生在形成和发展“四基”的过程中核心素养的达成和发展状况,在学生经历“发现和提出问题”“分析和解决问题”的过程中,综合考查“四基”“四能”与核心素养[1].笔者现将2023年浙江省金华市数学中考试题第24题的命制过程及思考整理成文,为从结构化视角设计试题做一些有益探索.

1 素材追溯

根据试卷命制的双向细目表,最后一道题目选择“图形与几何”的内容,并适度关联其他核心内容,以体现其综合性,让学生在独立探究图形性质的过程中,建立空间观念、几何直观,实现对推理能力等核心素养的全面考查.为此,查阅教材后,笔者选择浙教版《义务教育教科书·数学》八年级上册第2.3节“等腰三角形的性质定理”中的练习题作为素材研究的起点.

素材已知:如图1,在△ABC中,AB=AC,D为BA延长线上一点,DE⊥BC于点E,交AC于点F.求证:∠D=∠AFD.

图1

分析此素材以等腰三角形为背景,证明等角需要具备一定的推理能力.如图2,在边BC上取点H,满足HE=EC,联结DC,DH,AH,则△DHC也为等腰三角形.若H是边BC的中点,则DE,AH都是对应等腰三角形的“三线”(高线、角平分线和中线),实现了从“边”“角”的研究上升到“形”的研究.若改变点D的位置,则能实现特殊与一般的转化,使图形丰富有内涵,有想象空间.若联系抛物线的轴对称性,进行图形整合,则有拓展空间.

2 编制过程

命题组经过讨论,选择此素材的特殊位置,在直角坐标系中通过直观猜想、推理验证、坐标法分析等方法研究图形,体现数形结合,以期发现图形特征.

2.1 组合基本图形,探寻一般结论

选择学生熟悉的三边之比为“3∶4∶5”的直角三角形为基本结构,作为试题第2)小题的题干,尝试从边、角、形等角度出发研究图形,引导学生经历观察图形、发现和证明几何命题的过程.

第2问(题干)如图3,在平面直角坐标系中,OA=OC=4,OB=3,点P在直线AB上,已知PO=PC.

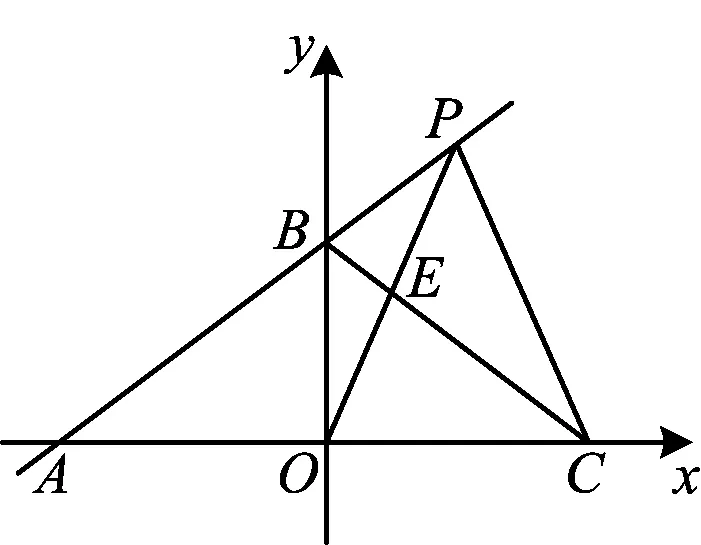
图3

分析从“边、角、形”等要素获得的结论:从“边”的角度分析,有BA=BC,OE=EP,EC=3BE等数量关系;从“角”的角度分析,有∠APO=∠BCP等;从“形”的角度分析,有△BAC与△POC是等腰三角形等图形特征,△BPE∽△BCP等图形关系.其中,从“边”的数量关系来看,“EC=3BE”这一结论更能体现思维的深度与广度,因此,命题组尝试将其作为设问的方向.

思路1用坐标法研究图形,体现数形结合.

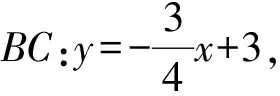
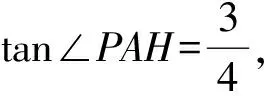
图4

思路2联系等腰三角形的特征,构造“三线”.

思路3联系相似的基本图形,得出AB=2BP后,作平行线构造全等或相似三角形.

方法4如图6,过点O作OF∥BC交AB于点F,则OF是△ABC的中位线,从而BC=2FO.易得△BPE∽△FPO,则FO=2BE,于是EC=3BE.

图6

事实上,除过点E外,过任何一个关键点作平行线构造相似图形都能证明该结论.这说明推理获得该结论的思路广泛,有考查的价值,并且能提炼出学生熟悉的几何图形,因此,将此结论的验证作为试题的第2问.

2.2 整合基本内容,挖掘特殊规律

进一步思考,若调整点P的位置,则存在△APC也是等腰三角形这一特殊情况,此时图形具有良好的数学结构.从“边、角、形”等角度研究,如图7,若增加“点D在线段AC上,且PD=PC,联结PD交BC于点E”的条件,还能得到“CE=CD,∠CDE=∠CED,△CDE为等腰三角形,△PDC∽△APC∽△CDE,△PEC∽△ADP”等结论,其中探究△CDE为等腰三角形、三角形相似存在性问题都比较常规,选择探究∠DPC=∠BAO的存在条件,由此,形成新的考查方向.

图7

第3问(初稿)如图7,在平面直角坐标系中,OA=OC=4,OB=3,点P在直线AB上,点D在直线AC上,PD=PC.试探究∠DPC=∠BAO时点P的位置.

图8

图9

分析将题目与抛物线进行整合,一方面,利用对称性确保PC=PD,间接表述题干,学生易于理解;另一方面,关注抛物线、等腰三角形的共性(对称性),分别从坐标分析、图形性质分析等角度出发寻找解决问题的思路,体现了方法的多样性,让学生关联相关知识以及解题经验,选择适合自己的方法完成求解.

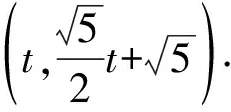
图10

方法1在Rt△APH中,利用勾股定理可得

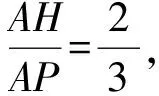
思路2从“角”的角度分析,记∠BAO=α.尝试在等腰△DPC中构造含α角的直角三角形,利用边的比例关系求解.

方法3如图11,过点D作DF⊥PC于点F.在Rt△PDF中,

图11

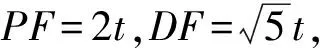
FC=PC-PF=t.

在Rt△DFC中,

即可求得交点P的坐标.

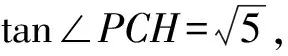
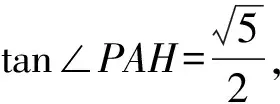
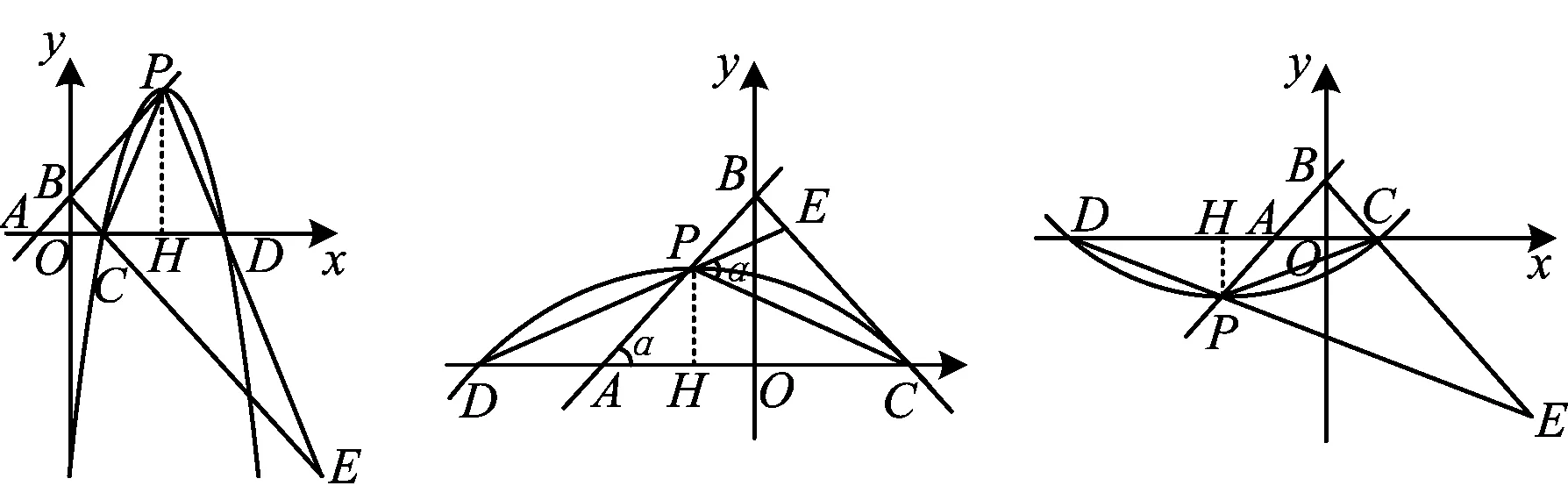
图12

图15

1)如图16,若抛物线经过原点O.

①求该抛物线的函数表达式;

2)联结PC,∠CPE与∠BAO能否相等?若能,求符合条件的点P的横坐标;若不能,试说明理由.

(2023年浙江省金华市数学中考试题第24题)

定稿后试题的第1)小题设置的入口较宽,体现基础,引导学生关注等腰三角形、抛物线的共同特征,从“边、角、形”的研究路径出发,为发现新的等腰三角形提供了方向.第2)小题为学生提供了探究、发现、思考的空间,需要学生完整画出图形,很好地考查了学生关联相关知识的能力和对这些知识的理解、掌握和灵活运用的程度,以及数形结合、分类讨论的思想[3].

3 命题反思

该试题的编制过程采用“关注内在结构,整合熟悉图形,关联研究路径,探究设问方向”的方法,不断尝试,经历“整合结构、形成结构、应用并反思结构”的过程,最终形成试题.该题外形简约,以等腰三角形、抛物线的轴对称为背景,以等角的存在性问题为探究方向,全面考查等腰三角形、直角三角形、抛物线等相关核心知识,问题探究层层递进,让学生经历用几何直观和逻辑推理分析问题和解决问题的过程,有效考查学生的几何直观、空间观念、推理能力等核心素养.(命制思路如图17所示.)

图17

3.1 明确考查意图,实现对知识与素养的考查

学业质量评估重视学生核心素养的达成和发展情况,这就需要设计体现结构化特征的试题内容,以引导学生对数学本质的理解,考查学生掌握“四基”的过程中所需要的推理能力、运算能力、几何直观和空间观念等.例如,推理是数学的基本思维方式,也是人们学习生活中常用的思维方式.试题的第1)小题涉及线段比的求值,让学生从“边、角、形”等角度去发现图形特征、图形蕴含的结论,在此过程中关联了不同的知识,产生了不同的思路、方法,说明该小题实现了“等腰三角形、相似图形、抛物线、函数表达式、点的坐标”等内容的结构化整合,也为第2)小题的解决提供了探究的路径,体现了对考查合情推理、演绎推理的重视.

3.2 创设适宜情境,符合认知水平和生活经验

此题依托等腰三角形和抛物线,求线段比值和探究等角存在的条件,这些都是学生熟悉的内容.第2)小题画出点P在不同位置时的各种图形(图12～14),需要借助几何直观,联系等腰三角形、抛物线的轴对称性.等角问题的探究与三角形研究的路径一致,对边、角的数量关系的分析,图形形状判别(等腰三角形)和图形关系判定(全等或相似),以及添加辅助线的方法(作平行线、等腰三角形的高线),都是学生在学习三角形、四边形中常见的方法.基于学生的经验,容易把复杂的数学问题变得简单、形象,形成解决问题的思路.让学生学会数学思考,学会用图形的运动与变化的方式去认识和理解问题,形成研究数学、学习数学的基本能力,进一步积累解决问题的经验.

3.3 设置合理问题,让学生充分经历探究过程

问题的设置与呈现,重点是对内容的结构化整合,注重数学知识与方法的层次性和多样性,有利于考查学生对数学概念、性质、关系、规律的理解、表达和应用,让学生经历探究发现、获得结果的过程,以考查学生的思维能力.在解决问题的过程中,不同的学生有不同的经验和几何直觉,选择的方法就会各显特色.第2)小题先通过角的研究,得出等腰三角形,再到直角三角形中利用三角函数、代数式表示3条边,比其他的方法简洁,并且形成当点P在不同位置时研究问题、解决问题的通法.即利用已知角在直角三角形中构造相关角,再转化为边的比例关系求解,这种方法有很大的灵活性和创造性,也是解决每一种情况的通法.这种方法的获得需要学生具有良好的数学思维习惯,同时也体现了方法的选择性,逐步加深探究,适合学生发展的需求.