几何画图追寻本质 深度探究享乐其中——一道自编题的思考

程 峰, 何漫天

(1.彭泽县钓鱼台中学,江西 彭泽 332700;2.彭泽县教体局教育发展中心,江西 彭泽 332700)

1 试题展现

例1如图1,已知△ABC和△DEF是全等的等边三角形,且点B,D,C,E在同一直线上.试仅用无刻度的直尺按要求完成以下作图(不写作法,保留作图痕迹).

图1

1)在图1(a)中,作出DC的中点;

2)在图1(b)中,作出以AB,BC为邻边的菱形.

(2023年江西省彭泽县九年级模拟考试数学试卷第14题)

此题是笔者为江西省彭泽县模拟考试提供的试题.从考后各校反馈的信息看,此题受到了较好的评价.下面笔者把对此题的思考和探究整理成文,与读者分享.

2 试题解答

本文主要讨论第2)小题.为了便于读者理解第2)小题的画法,笔者先介绍画法中用到的几个模型图(图2～5),限于篇幅,4个图中相关结论的证明略.

图2

图2说明AD∥BC,O是AC的中点,AD,BO的延长线交于点E,联结CE,则四边形ABCE是平行四边形.若AB=BC,则四边形ABCE是菱形.

图3说明四边形ABCD,DCEF都是平行四边形,对角线AC,BD交于点G,对角线DE,CF交于点H,GH与DC交于点M,则点M是DC的中点.

图4说明四边形ABCD,AEFD都是平行四边形,且点B,C,E,F在同一条直线上,对角线AC,BD交于点M,对角线DE,AF交于点N,MN与DC,AE分别交于点P,Q,则点P是DC的中点,点Q是AE的中点.

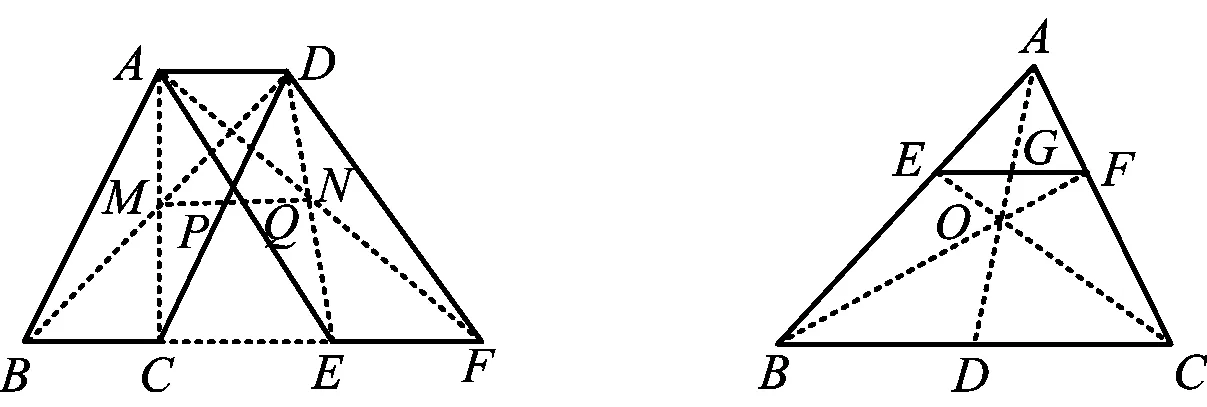
图4

图5说明在△ABC中,EF∥BC,BF,CE交于点O,联结AO,AO的延长线与BC,EF分别交于点D,G,则D,G分别是BC,EF的中点.反之,若AD是△ABC的中线,O是AD上任意一点,联结CO并延长交AB于点E,联结BO并延长交AC于点F,则EF∥BC.

第2)小题笔者提供的答案如图6～8所示.在阅卷过程中,有少数学生给出了如图9和图10所示的画法,显然,这两种画法(本质上是一种)也是正确的.阅卷结束后,笔者教学之余继续探究第2)小题的画法,又找到如图11～14所示的画法.其实,图9～14的画法与图6思路相同,都是先作出边AC上的中点,再作出菱形.

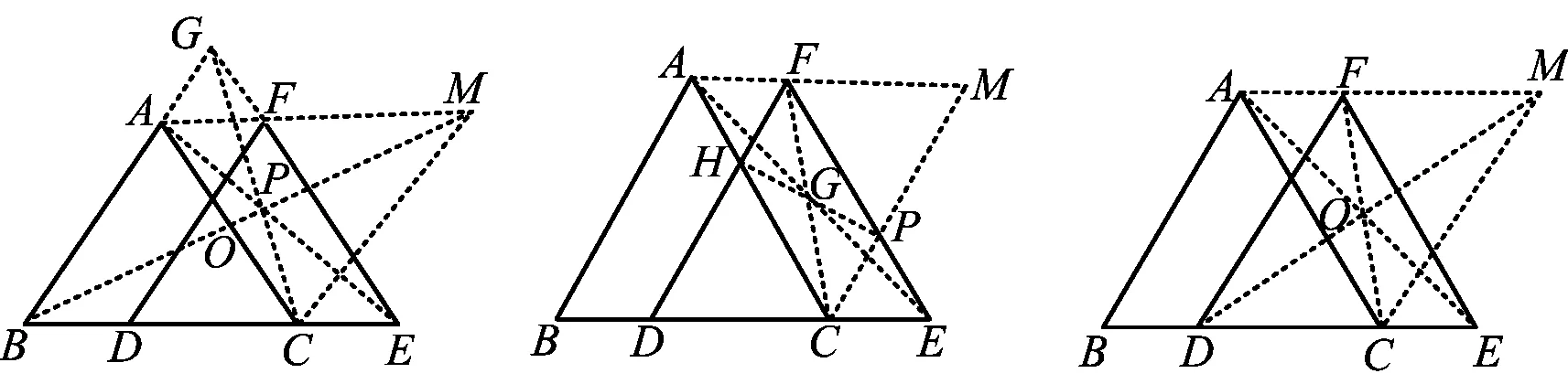
图6

图9

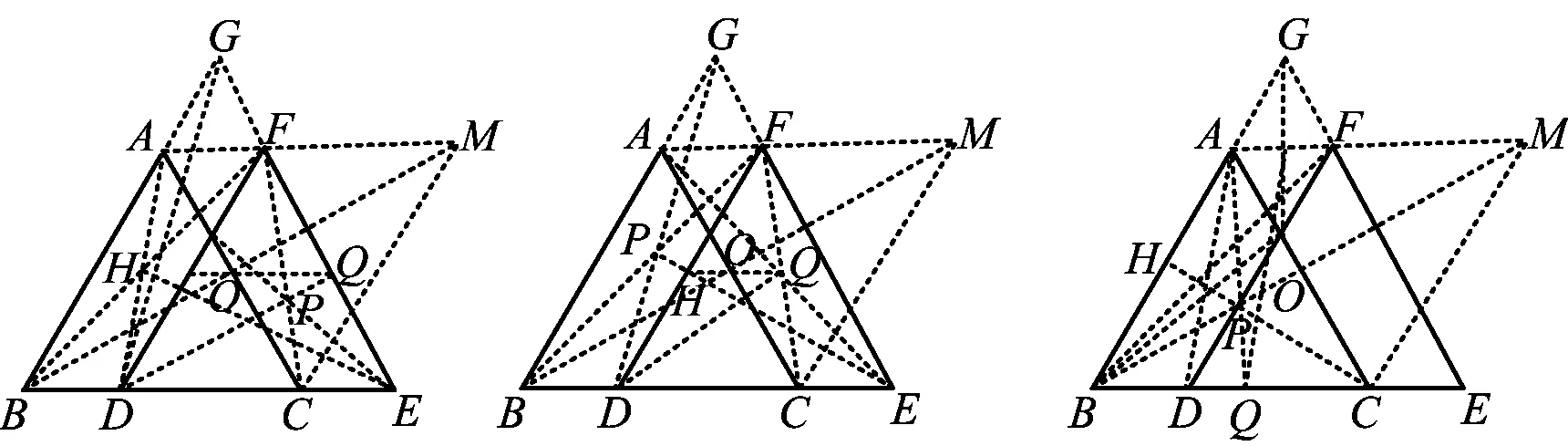
图12

3 试题再探

美国数学教育家波利亚说过:“没有一道题可以解决得十全十美,总还有值得我们探究的地方.”他还说过:“好题就像蘑菇,当你找到第一棵蘑菇后,要环顾四周,因为它们总是成堆生长的.”因此,笔者教学之余对此题进行了再探究,并得出了一个一般性的结论.

1)把图1(b)中的等边△DEF向下翻折,如图15,同样可以作出以AB,BC为邻边的菱形ABCM(画法提示:先画出以AB,BE为邻边的平行四边形ABEN,再画出菱形ABCM).

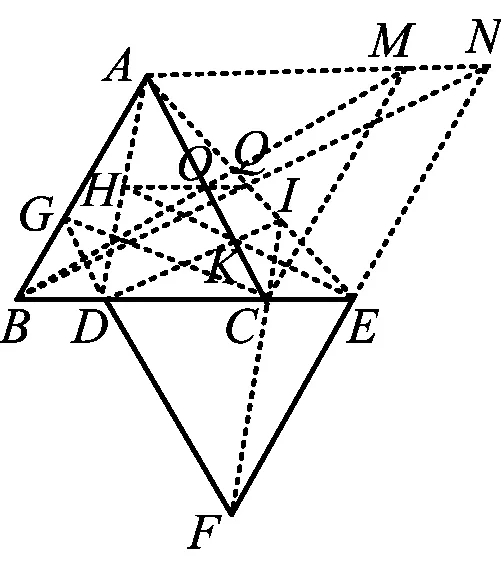
图15

2)把等边△DEF缩小,此时△ABC∽△DEF,是否还能画出以AB,BC为邻边的菱形呢?答案是肯定的,笔者历经一个月的持续思考,探究了两个等边三角形如图16～34的各种位置关系,发现均能作出菱形ABCM.

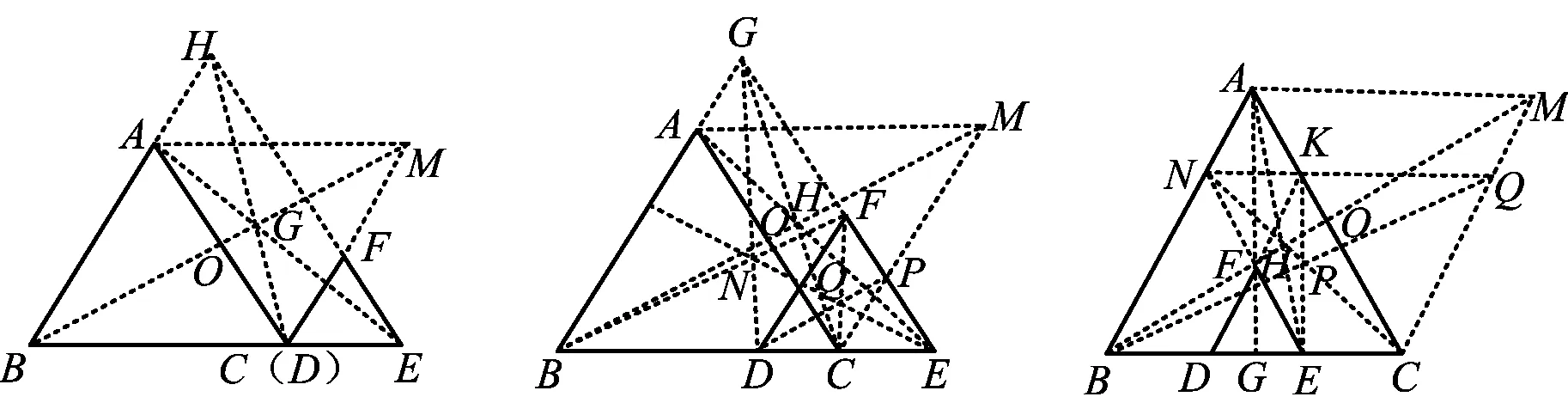
图16

图19

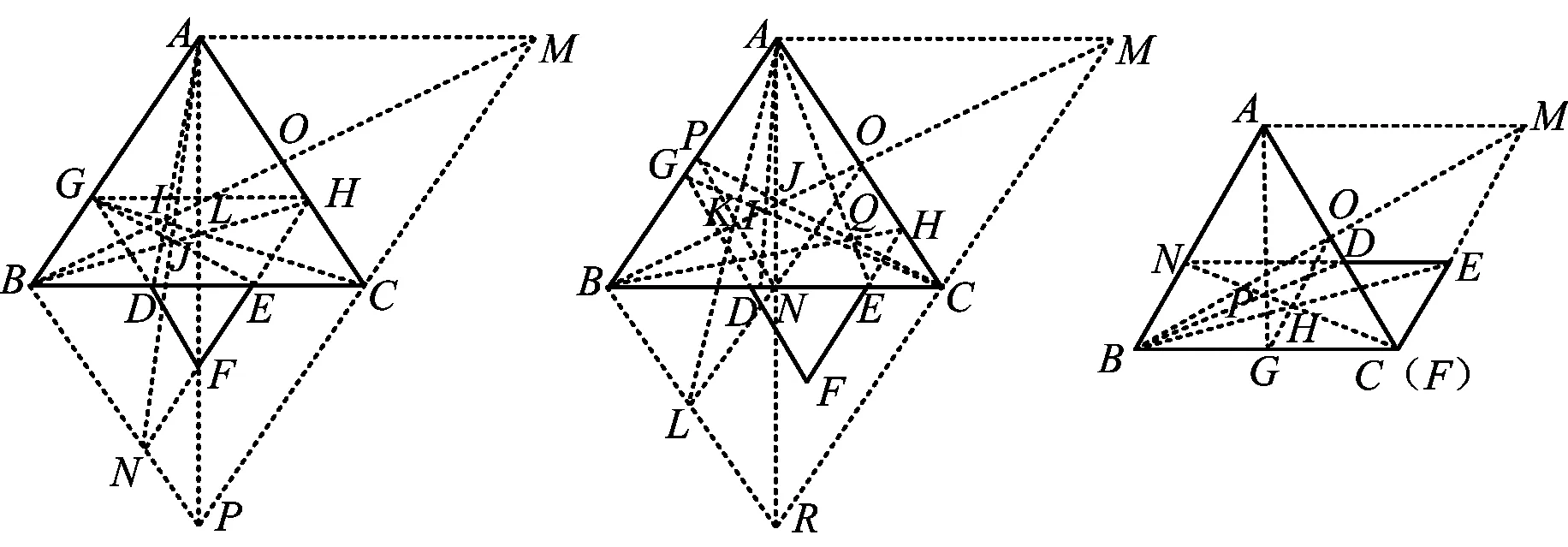
图22

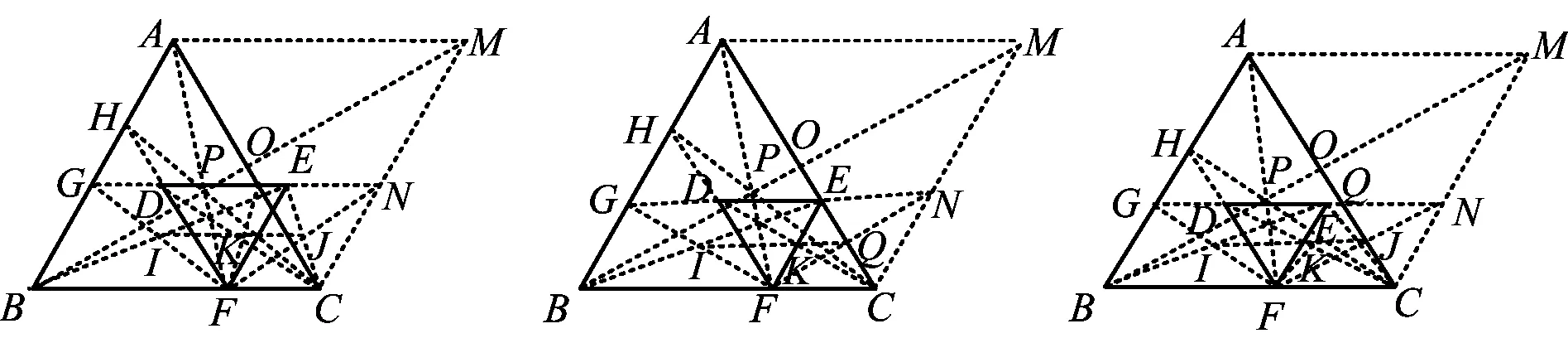
图25

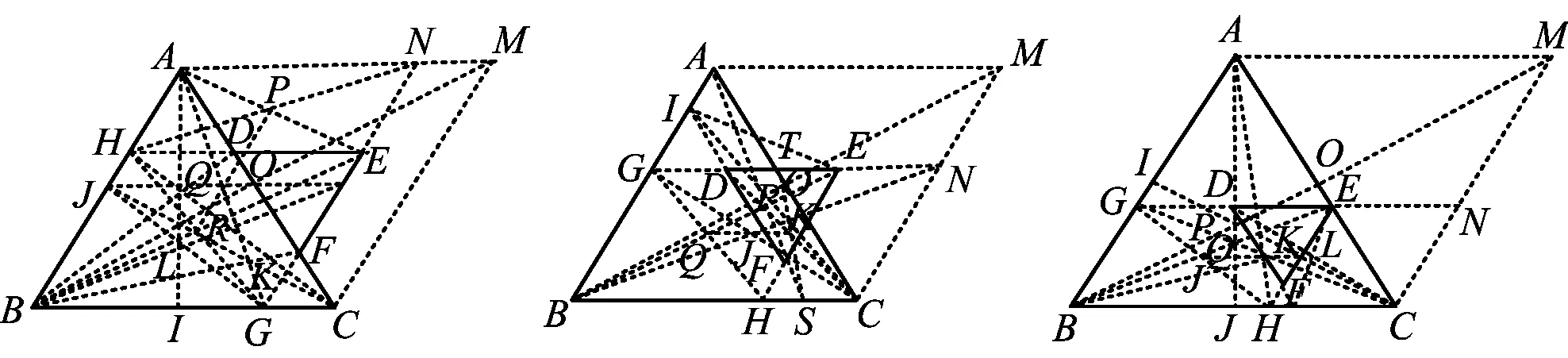
图31

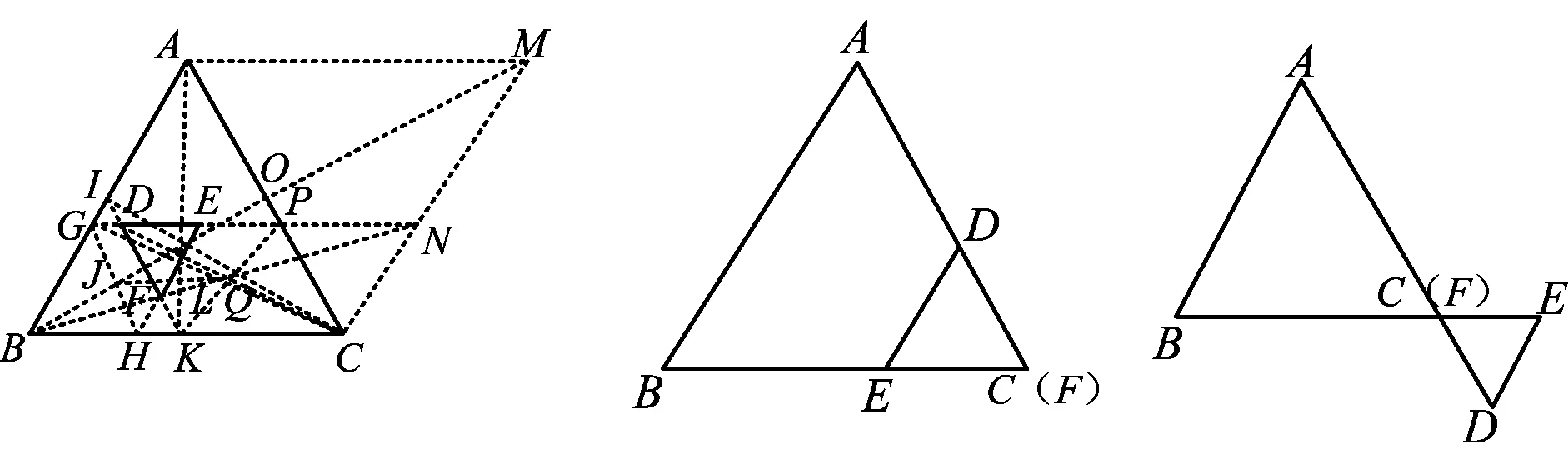
图34

结论当等边△ABC和等边△DEF全等或相似,且△DEF的两边或三边分别与△ABC的两边或三边平行时,都能画出以AB,BC为邻边的菱形.若△DEF只有一条边与△ABC的一边平行,则不能画出以AB,BC为邻边的菱形,如图35和图36所示.

评注1)上述画法中,有的图形有多种画法,有的图形笔者给出的可能不是最简的画法.2)上述图形的变化规律是:大三角形不动,小三角形从右往左移动,也就是从大三角形外移动到大三角形内.3)笔者认为,上述图形的探究由于添加的线段和交点较多,比较复杂,因此除了图16、图21外,其他图形不宜在课堂上向学生展示,但是适合教师探究.

4 陈题新探

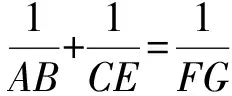
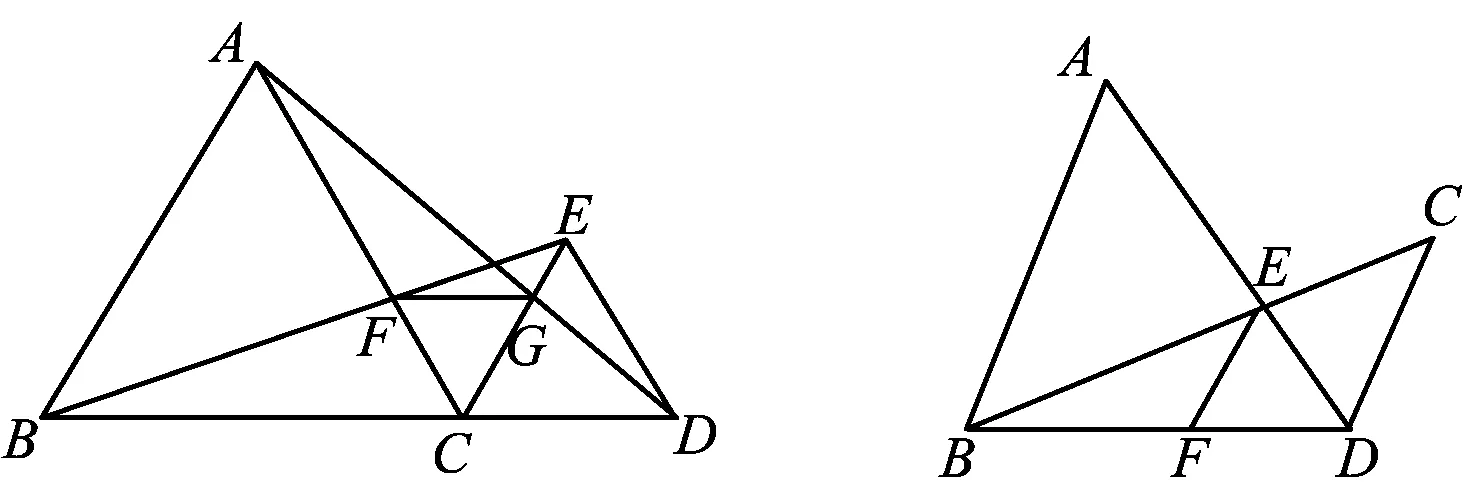
图37

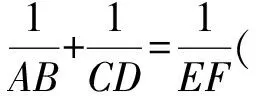
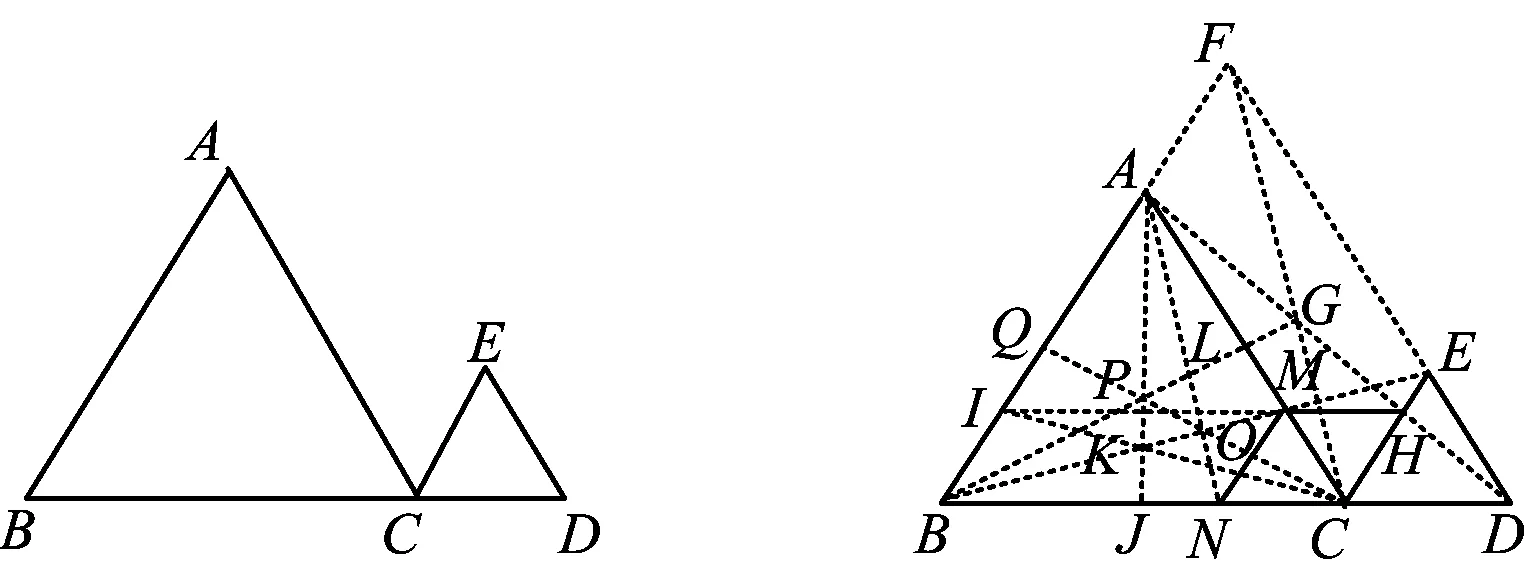
图39

5 几点思考

1)从编题的角度看,笔者认为例1受到较好评价的原因主要是:①此题的背景图和要画的图形都是初中阶段最常见的几何图形——等边三角形、菱形.它们的性质、判定都是学生熟悉并掌握的.学生见到此题会有一种“似曾相识”的感觉,因此题目的起点较低,第1)小题的得分率达到90%.②此题取材于含60°角的菱形,含60°角的菱形可以看作是两个全等的等边三角形组成,这种菱形是最常见的菱形之一.于是,笔者想到先把含60°角的菱形分割成两个全等的等边三角形,然后改变两个三角形的位置关系,还原(画)出菱形,考查学生的逆向思维,因此此题的落点较高.第2)小题的平均得分率只有40%,说明第2)小题对于大部分学生来说是很有难度的.

2)从题目功能看,只利用无刻度直尺画图问题是借助无刻度直尺在几何基本图形、网格或坐标系等几何背景中进行作图构思与研究,由此探究相关点、线、几何图形之间的特殊位置、形状及大小之间的关系,进而设置相关的问题与探究.无刻度直尺画图的实质是构造直线和点这两种基本图形,其中画直线的基本原理是两点确定一条直线,画点的基本原理是两直线交于一点,这对训练和培养学生几何直观、推理能力等核心素养有着极为重要的意义.如此题要画菱形,根据图形特征,容易想到先画出中点,再画出菱形,较好地考查了学生的几何直观能力、推理能力和创新能力.

3)从探究过程看,著名数学家陈省身曾说:“数学好玩.”教师应当享受探究与发现的乐趣,让解题不再是负担,而是享受;让解题过程不再沉冗烦躁,而是轻松愉快.也就是说,教师应该把一题多解、多题一解、一题多变、发现规律、提炼规律等当作是常态化教研,并享受其中的探究过程.教师的探究应该是自发的、内省的,应该有“超前意识”,是“源”于学生而又“高”于学生的,是“高屋建瓴”的.因此,引导学生有目的地探究的前提是教师更要有主动探究的意识和创新意识.另外,教师在探究过程中还可以发现美、挖掘美.例如,笔者把两个全等的等边三角形变为两个相似的等边三角形,在探究过程中思考了两个等边三角形所有可能出现的位置关系,并最终得出能画出菱形的一般规律,充分体现了“变中蕴含不变”的辩证思想.还有陈题新探的探究过程也是对数学美的发现和挖掘.当然,还可以把此题的两个全等的等边三角形变为两个全等或相似的等腰三角形继续探究,有兴趣的读者可以尝试.