组合赋权下的调心滚子轴承响应面MOGA优化模型
2024-02-21吴文群
吴文群
(三明医学科技职业学院 工程与设计系,福建三明 365000)
调心滚子轴承是机械系统中一种重要的精密传动部件,广泛应用于航空、航天、船舶、电力、石油化工等领域。随着社会经济的发展,调心滚子轴承的功能和性能也不断地得到提高,其技术和工艺也日趋成熟,成为各机械制造企业重点关注的对象之一。调心滚子轴承内圈通过与轴在滚动接触而形成一套完整的闭环摩擦副[1-2],这使得调心滚子轴承在工作过程中不可避免地受到各种因素的影响并表现出复杂和非线性的特性[3-4]。由于调心滚子轴承结构设计及综合性能要求严格,因此一直以来都是设计工程师们关注的重点内容之一。
文献[5]为了优化调心滚子轴承的应用性能,设计基于Kriging模型的调心滚子轴承优化模型。在考虑滚子轴承力学结构的基础上,将滚子轴承的多方向最小应力设置为目标函数,并根据轴承几何结构设置约束条件,利用Kriging模型对调心滚子轴承进行自适应优化,有效提升调心滚子轴承的综合力学性能。但在轴承受载后,两列滚道各有将近一半的滚子承受载荷,而且两列承载滚子数量和承载滚子位置角范围不同,两列滚道受到的载荷和应力不同,出现了偏载现象。文献[6]基于赫兹接触理论提出了一种新的简化轴承有限元模型。在考虑轴和轴承内圈过盈配合的基础上求解全局模型的滚子接触载荷分布。将求出的最大接触载荷对应的位移作为局部模型的边界条件,求解内圈的应力分布。当调心滚子轴承受到交变载荷时,其固有频率和各阶固有频率都会发生变化并引起内圈与轴之间响应面相互摩擦产生热应力而导致调心滚子轴承失效。
为了解决上述问题,提出一种组合赋权下的调心滚子轴承响应面MOGA优化模型。通过组合赋权的方式对响应面结构及其应力分布进行设计,采用MOGA优化响应面有限元模型,达到最优量优化,提升轴承整体综合性能与可靠性。
1 组合赋权模型的构建与计算
1.1 建立调心滚子轴承响应面客观赋权模型
考虑到传统调心滚子轴承响应面赋权多样性分析过程中,为了更好地简化赋权计算过程,在层次结构响应面参量优化评估方面,忽略了实际响应面作用结构评估差值的影响,造成赋权结构面与响应面之间权重及其各项指标无法达到平衡。因此在提出优化模型中为了更好地体现实际响应面参量,对其进行客观赋权模型构建,具体如下。
令第p个结构面与第q个响应面决策的近似度判定指标为距离dpq(p,q=1,2,…,T),则:
dpq=d(Y(p),Y(q)),
(1)
其中dpq相关系数量的约束条件需满足:dpq=dqp≥0。dpq对应系数取值越小,说明其对应Y(p)系数值与Y(q)系数值分布结构面距离越近,即结构面与响应面的参量越统一,当且仅当dpq=0且p≠q时,结构面与响应面上的权重参量完全一致。
令第t个响应面决策与其剩下的所有响应面决策的近似度判定指标为dt,则:
(2)
整合上述参量可知,第t位响应面的客观决策权重系数λt为:
若dt=0,则:
(3)
若dt≠0,则:
(4)
其中j=1,2,…,T。
通过计算参量之间的客观联系可知:当dt对应系数取值越大时,说明其对应的响应面与其他响应面之间的权重系数差异越大,相应客观赋权决策系数越小;当dt对应系数取值越小时,说明其对应的响应面与其他响应面之间的权重系数差异越小,相应客观赋权决策系数越大。继而实现了突出响应面参量对结构面客观赋权的分配统一,增强响应面赋权合理性。
(5)
根据现阶段已知历史经验,调心滚子轴承响应面客观赋权决定条件包含响应面质量特性X1、结构面应力信息X2、响应结构差值X3、评估系数量X4、主观权重X5五个指标。通过翻阅大量资料,通过相邻参量的配对对比,分别对每个响应面所对应的结构面应力分布进行客观权重判断,并对其矩阵特征向量与决策加权值进行求值,由式(5)得到调心滚子轴承响应面客观权重模型向量Y*=(0.270 6,0.143 8,0.088 2,0.027 2,0.015 7)。
1.2 响应面线性应力分布分析
根据上述客观赋权模型对其响应面线性应力分布情况进行分析,以此获得更为精准的MOGA优化所需参量。通过Hertz接触理论[7-8]对两个长度相同且二者呈平行关系的圆柱体接触面进行结构面应力分析,可知其接触面压力的分布形态呈半椭圆柱形态扩散,如图1所示。已知调心滚子轴承的接触面通常为线接触形态[9-10],其对应响应面的压力分布等同于呈半椭圆柱形态扩散范围。

图1 接触面压力的分布形态
由此可得到调心滚子轴承响应面径向负荷力b(mm)为
(6)
式中Q代表调心滚子与结构接触面之间的法向接触负荷;l代表调心滚子接触面长度;∑ρ代表响应面对应曲率系数及其相关函数;ξ代表泊松比;下角标1、2代表响应面不同位置上的应力分布区域;E代表区域弹性系数。
响应面中心位置分布的轴向负荷力P(MPa)的函数关系式为
(7)
对于调心滚子轴承结构的响应面径向负荷力,可对其进行数值代入,经过简化计算后,表达为
(8)
(9)
1.3 建立响应面有限元模型
将上述分析所得参量作为响应面有限元模型建立依据,对其响应面最优接触结构量进行有限元模型构建,其中以响应面受力角b1、调心滚子半径b2、调心滚子长度P3与调心滚子外半径P4作为模型构建初始参量。以响应面结构点上的径向负荷力b、轴向负荷力P作为优化系数[11-12],结合调心滚子轴承响应面几何结构及其约束[13],采用多目标遗传算法(MOGA)对其优化。
优化后的有限元模型如式(10)所示:
(10)
模型参量的约束条件如式(11):
(11)
通过插值计算,提升模型有限元精度,计算公式为
y(x)=f(x)+Z(x),
(12)
式中y(x)代表插值影响系数的未知函数,f(x)代表相似空间变量的全局函数,Z(x)代表均值系数值为零、方差系数值为零、协方差系数值为非零情况下的有限元高斯随机正态分布函数。
插值优化过程中通过可决参量R2、残差相对量MMR、均方差系数RMSE、相对均方差系数RRMSE、绝对均方差系数RMAE、绝对均方差均值RAAE作为判定指标量,完成插值优化过程的拟合,对应拟合过程的函数表达式如下:
(13)
(14)
(15)
(16)
(17)
(18)
1.4 响应面MOGA优化模型构建
根据上述优化参量表现出的参量特征,结合调心滚子轴承实际工作状态下的响应面运动力及其结构特点,将调心滚子垂直方向上的两种应力变化定义响应面MOGA优化变量,通过滚子与运动槽位之间的应力最小载荷差值、响应面内侧滚子最小载荷、响应面最大转角为多优化目标结构面。
考虑到实际应用过程中调心滚子轴承作用力分布的响应面多以前部应力分布较多[14-15],造成响应面末端滚子损耗过大,直接影响轴承使用寿命。因此在MOGA优化过程中,将其垂直方向上的最小径向负荷力bmin和最小轴向负荷力Pmin作为响应面的优化目标,减小滚子前段结构应力载荷和末端滚子的受力,并减少信载颠簸引起的摩擦和磨损,均匀分配响应面载荷系数分布,避免出现局部应力过大的情况。优化后的调心滚子轴承滚子末端响应面上的最小径向负荷力bmin可表示为
(19)
式中R1代表轴心移动后滚子末端响应面上的载荷;a1j代表垂直关系下直线分布在响应面末端的载荷;yj代表第j个滚子结构响应面上的垂向变位量。
优化后的调心滚子轴承滚子前端响应面上的最小轴向负荷力Pmin可表示为
(20)

为保证优化面对应不同优化参量时,所得优化结果保持一致,响应面MOGA优化模型的统一函数关系式为
(21)

2 应用测试
通过设计仿真测试场景,对提出模型优化效果进行相关指标对比分析,通过与对比样本模型相同条件下所得指标结果对比分析,证明提出模型的有效性。其中,对比样本模型分别来源于文献[5]基于Kriging模型的调心滚子轴承优化模型与文献[6]基于赫兹接触理论的简化轴承有限元模型;为了测试过程描述简洁,将其分别简称为对比模型A与对比模型B,提出的组合赋权下的调心滚子轴承响应面MOGA优化模型简称为目标模型C。
2.1 测试条件及其相关参量
为了保证测试结果的严谨性与其客观性,仿真测试工具采用轴承结构应力测试平台(BSSTS)完成设计测试下的所有测试内容。测试轴承样本参数及其测试环境参数,详见表1。

表1 测试条件及其相关参量
根据表1参量配置,测试平台环境结构,如图2所示。

图2 测试平台环境结构
2.2 响应面应力分布测试
分别由对比模型A、对比模型B、目标模型C对轴承测试样本进行响应面应力分布优化,优化在独立无扰动环境下完成,完成优化后通过仿真测试平台对其优化效果进行响应面应力分布测试,测试结果如图3所示。

图3 不同方法优化后的调心滚子轴承响应面应力分布解释结果
根据图3所示数据对应曲线分布情况对比可知,图3(d)所反映数据对应对比优化前的轴承样本响应面应力分布优化效果。根据其曲线分布来看,曲线整体毫无规律可循,响应面应力分布不均。图3(a)所反映数据对应对比模型A的轴承样本响应面应力分布优化效果。根据其曲线分布来看,最大应力曲线与响应面应力曲线整体均为下降趋势,对应性能为衰减状态。根据两条指标曲线的起始值与终止数值来看,优化效果并不理想,数值所在值域偏低。
按照上述分析方式,分析图3(d)对应对比模型B的轴承样本响应面应力分布优化效果可知,其初始值与终止数值分布值域与对比模型A相同;究其曲线整体趋势,对比模型B的性能远不如对比模型A,关键在于曲线抖动次数较多,且较为集中,说明在响应面上的某一点应力系数超出其均值系数甚至最大系数,由此看来该模型的优化效果并不理想;
基于上述两组对比模型的测试结果及其分析,反观图3(c)中目标模型C测试曲线,整体平稳,起始值与终止值差值系数小,且整体值域提升明显,说明在响应面应力分布优化方面效果明显;加之双曲线趋势特征极为相似,更加说明目标模型C在参量统一方面的效果显著。
综上所述,响应面应力分布测试中目标模型C的各项指标满足测试相关指标要求,所得结果符合相关标准,通过该项目测试。
2.3 连续性暴力压力测试
为了验证提出模型优化后响应面应力分布能够满足实际应用场景下极端条件,通过连续输出最大应力参量,且将测试环境的温度调整为样本条件的最大值,即响应面温度536摄氏度,为了保证测试安全,测试通过仿真工具,配合大数据模拟计算技术共同完成。测试共计连续释放10组应力数据,不同优化模型测试结果,如图4所示。
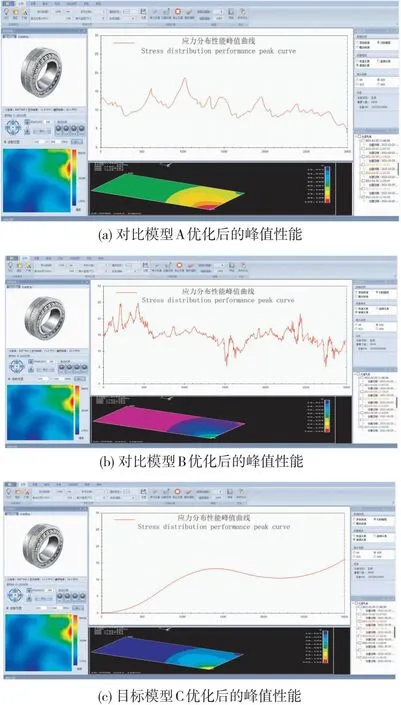
图4 连续性暴力压力测试结果
对图4中(a)、(b)、(c)图的数据对比分析:1)对比图4(a)、(b)、(c)下性能曲线数据窗口可知,目标模型的曲线最为平滑,无任何波动;对比模型B波动最为剧烈,且波动次数最多;对比模型A存在波动,但波动周期相比对比模型B较长;因此可以说明目标模型C的整体应力抗压性能最好。2)对比图4(a)、(b)、(c)下压力分布窗口可知,对比模型A压力分布过于集中一点;对比模型B外部压力分布较为集中;目标模型C整体受力相对均匀,由此可以判定目标模型C的响应面优化更为科学合理。
3 结语
通过对调心滚子轴承响应面的组合赋权优化,实现了提升响应面应力分布均衡性,延长使用寿命的效果。模型的提出为多种类轴承响应面结构优化,提升产品品质有着重要的推动作用。但是,从优化结构参量方面看,提出模型还存在局部缺陷。根据轴承不同材质膨胀系数不同的特征,模型中采用的结构面MOGA优化约束对应的膨胀系数为固定值,因此在实际应用过程中会因为膨胀系数差异,造成最终优化结果出现局部应力分布误差。为了避免这一缺陷对其整体优化效果的影响。可以尝试采用动态约束函数,自适应不同膨胀系数,以此确保模型的最佳优化效果。
