一个大Lyapunov指数四维超混沌系统分析及同步
2024-02-21杨旦旦邓林
杨旦旦 邓林
(四川建筑职业技术学院 土木工程系,四川德阳 618000)
混沌是非线性系统中表现确定性、类随机的过程,由于对初值具有敏感的依赖性而广泛应用于保密通信、图像加密等方面。Lyapunov指数表示相空间相邻轨迹的平均指数发散率,是刻画非线性系统混沌特征的有效方法。普通的混沌系统有一个正的Lyapunov指数。而超混沌系统是具备至少2个正的Lyapunov指数的混沌系统,其不稳定性程度比普通混沌更高,动力学行为比普通混沌更加难以预测,因此有更高的应用价值。从超混沌概念被提出以来,研究人员对其研究取得了许多新成果[1-12]。文献[1-3]构造和研究了五维或五维以上超混沌系统,但是五维或五维以上的系统出现超混沌的可能性比四维系统出现超混沌的可能性要高。文献[4-12]构造和研究了四维的超混沌系统,但是其最大和第二大的Lyapunov指数都较小。有较大正Lyapunov指数的四维超混沌系统比较稀有。本文在前人的基础上给出了一个新的最大Lyapunov指数大于18、第二大的Lyapunov指数大于3的四维超混沌系统,分析了该系统的耗散性、平衡点的稳定性,用Lyapunov指数谱、相图等分析手段研究了系统各参数对系统的动力学特性的影响,设计了一种线性反馈控制器实现了该超混沌系统的混沌同步。
1 新超混沌的系统模型
文献[13]给出的混沌系统的动力学方程如下:
(1)
在此基础上,构造如下四维系统:
(2)
其中,x,y,z,w为系统的4个状态变量;a,b,c,e,f,g,h,k,m,r为系统参数。参考文献[14]中计算连续系统Lyapunov指数的方法计算此系统的Lyapunov指数,当选取参数(a,b,c,e,f,g,h,k,m,r)=(50, 15, 50, 30, 110, 1, 1, 10, 60, 100)时,该系统的Lyapunov指数为λ1=18.889 2,λ2=3.137 0,λ3=0,λ4=-96.923 4,有两个大的正的Lyapunov指数,并且所有Lyapunov指数的和小于零,其Lyapunov维数为3.227 3,说明此时系统达到超混沌状态。对应的吸引子相图如图1所示。
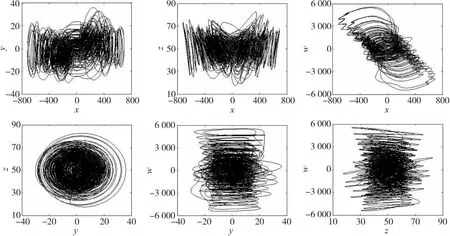
图1 系统的超混沌吸引子相图
2 系统的动力学分析
2.1 系统的对称性
存在一个对称变换F∶(x,y,z,w)→(-x,-y,z,-w),在变换F的作用下具有不变性,即系统关于z轴对称,并且这种对称性对所有的系统参数均成立。
2.2 系统的耗散性及吸引子的存在性
-75<0,可见该系统是一个耗散非线性系统,系统的状态是有界的,并以指数形式e-75收敛。当时间趋于无穷时,包含系统轨线的小体积元以指数速率收缩到零,系统的轨线会被限制在一个极限子集上,说明了吸引子的存在性。
2.3 平衡点及其性质
解方程组
可以得到系统的平衡点,用Matlab计算得到系统的平衡点为O(0,d,0,5d),其中d为实数。系统的Jacobi矩阵为
当d=0,将平衡点O(0,0,0,0)代入系统的Jacobi矩阵,得到对应的4个特征根为-78.989 8,18.989 8,0,-15。其中有一个为正值,所以O(0,0,0,0)是不稳定的鞍点。
2.4 系统参数对系统Lyapunov指数谱的影响
Lyapunov指数是动力系统相邻运动轨线分离程度的一种度量。判断系统运动状态的一种常用方法就是计算系统的Lyapunov指数。1)当系统收敛于稳定平衡点,系统所有的Lyapunov指数为负;2)当系统处于周期状态,系统最大的Lyapunov指数为0,其余Lyapunov指数为负;3)当系统处于拟周期状态,系统有2个Lyapunov指数为0,其余Lyapunov指数为负;4)当系统处于混沌状态,系统有1个正的Lyapunov指数,有一个Lyapunov指数为0;5)当系统处于超混沌状态,系统有2个或2个以上的正的Lyapunov指数,有一个Lyapunov指数为0。为了分析系统参数对系统(2)运动状态的影响,这里计算了改变一个参数而固定其余参数时系统的Lyapunov指数谱。从Lyapunov指数谱随参数变化判断系统作何种运动的参数区间,重点考虑作混沌和超混沌运动的参数区间。
系统是四维的,因此有四个Lyapunov指数。判断是否为混沌运动,只需看最大的Lyapunov指数L1是否大于零(数值计算的原因,这里给定一个下界0.05,即如果L1不小于0.05,判断为混沌运动)。判断是否为超混沌运动,只需看第二大的Lyapunov指数L2是否大于零(数值计算的原因,这里也给定一个下界0.05,即如果L2不小于0.05,判断为超混沌运动)。下面给出各参数变化时,系统作混沌运动和超混沌运动的连续参数区间。图2给出了a,b,c,e分别变化时系统的Lyapunov指数谱L1~L2。图2(a)给出系统参数(b,c,e,f,g,h,k,m,r)=(15,50,30,110,1,1,10,60,100),a∈[-20,400]时系统的Lyapunov指数谱L1~L2;计算结果表明,当28≤a≤400时,系统作混沌或超混沌运动,特别地当28≤a≤400时系统作超混沌运动。图2(b)给出系统参数(a,c,e,f,g,h,k,m,r)=(50, 50, 30, 110, 1, 1, 10, 60, 100),b∈[1, 201]时系统的Lyapunov指数谱L1~L2;计算结果表明,当1≤b≤61或83≤b≤141时,系统作混沌或超混沌运动,特别地当13≤b≤43时,系统作超混沌运动。图2(c)给出系统参数(a,b,e,f,g,h,k,m,r)=(50, 15, 30, 110, 1, 1, 10, 60, 100),c∈[-10, 99]时系统的Lyapunov指数谱L1~L2;计算结果表明,当26≤c≤79或95≤c≤99时,系统作混沌或超混沌运动,特别地当32≤c≤79或95≤c≤99时,系统作超混沌运动。图2(d)给出系统参数(a,b,c,f,g,h,k,m,r)=(50, 15, 50, 110, 1, 1, 10, 60, 100),e∈[-20, 170]时系统的Lyapunov指数谱L1~L2;计算结果表明,当-10≤e≤144或148≤e≤170时,系统作混沌或超混沌运动,特别地当22≤e≤144或148≤e≤154时,系统作超混沌运动。
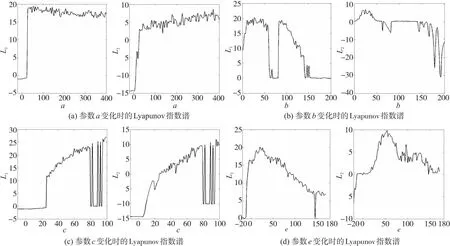
图2 系统参数a,b,c,e分别变化时系统的Lyapunov指数谱
图3给出了f,g,h,k分别变化时系统的Lyapunov指数谱L1~L2。图3(a)给出系统参数(a,b,c,e,g,h,k,m,r)=(50,15,50,30,1,1,10,60,100),f∈[-20,400]时系统的Lyapunov指数谱L1~L2;计算结果表明,当-16≤f≤220或360≤f≤400时,系统作混沌或超混沌运动,特别地当16≤f≤180时,系统作超混沌运动。图3(b)给出系统参数(a,b,c,e,f,h,k,m,r)=(50,15,50,30,110,1,10,60,100),g∈[1,100]时系统的Lyapunov指数谱L1~L2;计算结果表明,当1≤g≤20时,系统作混沌或超混沌运动,特别地当g=1时,系统作超混沌运动。图3(c)给出系统参数(a,b,c,e,f,g,k,m,r)=(50, 15, 50, 30, 110, 1, 10, 60, 100),h∈[1,201]时系统的Lyapunov指数谱L1~L2;计算结果表明,当1≤h≤201时,系统作混沌或超混沌运动,特别地当1≤h≤201时,系统作超混沌运动。图3(d)给出系统参数(a,b,c,e,f,g,h,m,r)=(50,15,50,30,110,1, 1,60,100),k∈[0,50]时系统的Lyapunov指数谱L1~L2;计算结果表明,当0.5≤k≤2.5或5≤k≤21.5时,系统作混沌或超混沌运动,特别地当0.5≤k≤2.5或5≤k≤13时,系统作超混沌运动。
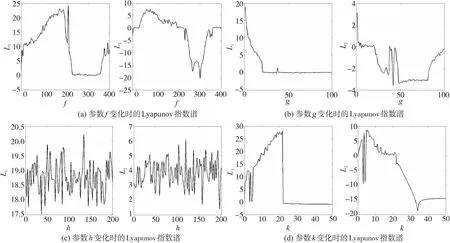
图3 系统参数f,g,h,k分别变化时系统的Lyapunov指数谱
图4给出了m,r分别变化时的系统的Lyapunov指数谱L1~L2。图4(a)给出系统参数(a,b,c,e,f,g,h,k,r)=(50,15,50,30,110,1,1,10,100),m∈[2,302]时系统的Lyapunov指数谱L1~L2;计算结果表明,2≤m≤80或182≤m≤278时,系统作混沌或超混沌运动,特别地当14≤m≤74时,系统作超混沌运动。图4(b)给出系统参数(a,b,c,e,f,g,h,k,m)=(50,15,50,30,110,1,1,10,60),r∈[-10,260]时系统的Lyapunov指数谱L1~L2;计算结果表明,74≤r≤224时,系统作混沌或超混沌运动,特别地当74≤r≤224时,系统作超混沌运动。

图4 系统参数m,r分别变化时系统的Lyapunov指数谱
3 典型参数值的数值模拟
Lyapunov指数无法直观看到系统作何种运动,而吸引子相图能直观看到系统作周期运动还是混沌运动。因此本节针对不同的典型的基本参数,数值模拟得到对应的吸引子的相图。由于参数较多,这里以参数b变化为例,其余参数保持和图2(b)中一样。b的变化区间为[1, 201]。6个典型b值下系统的吸引子在x-y平面的相图如图5所示。结合Lyapunov指数谱可知,当b=1时,系统成混沌态;当b=13时,系统成超混沌态;当b=63时,系统成周期态;当b=65时,系统成拟周期态;当b=127时,系统成混沌态;当b=197时,系统成周期态。
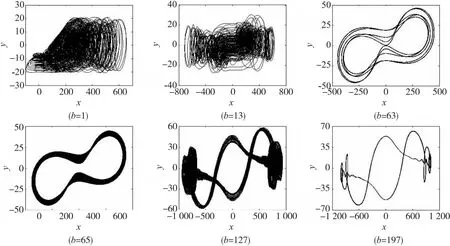
图5 不同的b值下系统吸引子的相轨迹在x-y平面的投影
4 超混沌同步
混沌同步是指一个系统(响应系统)的混沌动力学轨道收敛于另一个系统(驱动系统)的混沌动力学轨道,以致两个系统在以后的时间里始终保持步调一致。混沌同步是实现保密通信的关键。而超混沌同步是驱动系统和响应系统均为超混沌系统的混沌同步。下面将对本文讨论的超混沌系统实现超混沌同步。
设驱动系统为
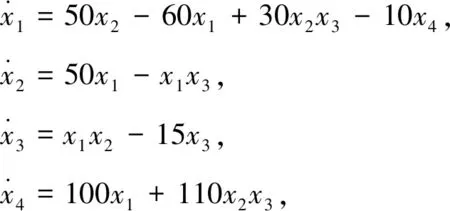
设驱动变量为x2,构造响应系统为
其中,p1、p2为待设计的反馈控制器。
设误差变量为
则误差系统可化为
选取线性反馈控制器p1=-10e2、p2=-10e4,则误差系统可化为

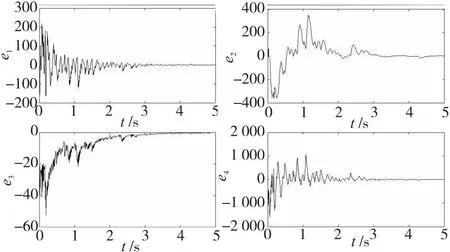
图6 同步误差曲线
5 结语
本文设计了一个新大Lyapunov指数四维超混沌系统。分析得到新系统的耗散性和平衡点的稳定性。计算了系统各个参数变化时系统的Lyapunov指数谱,从而得到系统作混沌运动和超混沌运动的参数变化区间。普通的混沌系统有一个正的Lyapunov指数,对初值的敏感使之在保密通信等领域有很大的应用价值。而超混沌系统由于有不止一个正的Lyapunov指数,所以对初值的敏感性比普通的混沌系统更强,所以在上述方面比普通的混沌系统有更大的应用价值。本文研究的超混沌系统在宽泛的参数区间表现出的混沌和超混沌特性可以给基于混沌和超混沌理论工程应用提供丰富的选择。用相图直观研究得到系统随参数变化时的运动形式。设计了一种线性反馈控制器实现了该超混沌系统的混沌同步,结果表明该同步方法快速有效、结果稳定。所得结果为该超混沌系统在混沌保密通信等领域中的应用提供了理论参考。
