基于Arnold变换的抗截获波形设计方法

陈 凤,杨 阳,程建军,朱立东,张 勇,4

(1.电子科技大学 通信抗干扰全国重点实验室,四川 成都 611731;2.成都流体动力创新中心,四川 成都 610072;3.中国人民解放军32040部队,青海 海东 810889;4.成都信息工程大学 通信工程学院,四川 成都 610225)

0 引言

由于卫星通信信道的开放性,通信信号的安全难以保证,设计具有抗截获性能的通信信号十分必要。在卫星通信中,最常见的抗截获传输方法是扩频通信[1-3]。扩频信号通常把有用信息隐藏在背景噪声中传输,加上传输过程中噪声和干扰的作用,以及扩频码的隐蔽性,使得扩频信号具有一定的安全通信能力。但由于扩频信号的扩频码是伪随机的,具有周期特性[4],目前已经有很多成熟的针对扩频技术的检测手段[5],例如：能量检测法、高阶累积量法、时延相关法、谱相关法等。因此传统的扩频传输技术很容易被非合作方检测到。

针对传统扩频传输技术存在易被截获等问题,本文在扩频技术的基础上,提出了一种基于Arnold变换的抗截获波形设计方法。该方法从有用信号本身出发,对信号的频域数据进行处理,即采用Arnold变换将有用信号在频域进行置乱,破环有用信号的周期性,使得其在时域上更接近杂乱的噪声信号。由于传统的扩频信号能很好地隐藏在噪声中,置乱后的扩频信号隐藏在噪声中更不易被发现,从而保证了信号的抗截获性能。

1 Arnold变换

扩频信号的子带置乱相当于将传统扩频信号进行加密的过程。在数字图像处理领域有很多图像的置乱算法,如Arnold变换[6-8]、幻方变换[9-10]、Baker变换[11]、Standard映射[12]等。其中Arnold变换是最经典的置乱方法,其方法简单、易于理解和实现,已经在图像领域得到了充分的应用。本文将Arnold变换与通信信号传输结合,以提高信号传输的安全性。

Arnold变换又称为“猫脸变换”,利用Arnold变换可以对图像进行置乱,使原本有意义的图像变成一张无意义的图像。实际上,Arnold变换是对矩阵进行变换,因此,该变换不仅可以用于图像置乱,也可以用于其他矩阵类型的数据。

Arnold变换可以抽象为在平面单位正方形内绘制一个猫脸图像,通过这一变换使得猫脸图像由清晰变得模糊[6]。将图像看作一个N×N的矩阵(本文主要讨论图像为正方形的情况),对矩阵中的每个坐标点(x,y)进行变换,具体变换方法如式(1)所示。

(1)

式中：mod为取模运算,N为正方形图像的边长,(x′,y′)为像素点(x,y)变换后的坐标。一个图像矩阵,通常一次Arnold变换不能达到理想的置乱效果,需要对矩阵进行连续多次的变换,使图像达到最“混乱”的程度。

Arnold变换存在逆变换[13-14],经过t次Arnold变换后的数据可以通过t次逆变换进行恢复,其逆变换过程如式(2)所示：

(2)

Arnold变换具有周期性[8,15],即对图像连续进行Arnold变换,最终又能得到原图像。变换周期和图像的尺寸N有关,不同尺寸N对应的变换周期如表1所示。鉴于此,Arnold变换使得矩阵的“混乱”程度是一个先增大再降低的过程,因此要得到最“混乱”的图像,需要找到使图像矩阵的“混乱”程度最大的变换次数t。将以上原理应用于通信数据中,同样需要找到最优的变换次数t,使得信号矩阵的混乱程度最大。

2 系统模型

为了提高扩频信号的抗截获性能,研究了对扩频信号频带进行子带置乱的方法。该方法借助Arnold变换的思想,将信号频域数据视为一个待处理矩阵,对不同子带的数据进行打乱,以达到子带置乱的目的。

系统的大致流程为：在发送端,基于Arnold变换,对扩频后的信号频带进行子带划分,并对各个子带进行一定程度的置乱,然后再进行无线传输;在接收端,先对接收信号进行子带乱序恢复,再进行整个扩频信号的解调与解扩。

通信系统流程如图1所示,其中图1(a)表示简要的通信过程,蓝色部分表示本文中主要涉及的方法,图1(b)表示子带置乱与置乱恢复的流程。

(a) 信号发送及接收流程图

(b) 子带置乱与子带恢复流程图

图1(b)中,在信号发送端直接采用对扩频信号的快速傅里叶变换(Fast Fourier Transform,FFT)值进行置乱的方法,使用均匀划分的方式对信号进行子带划分,将划分后的信号频段进行Arnold变换。

由于Arnold变换本质上是一种“位置置换”的变换,因此,对于扩频信号的频谱数据来说,Arnold变换是一种非线性变换。该方法以扩频信号子带乱序发送的方式打乱了原始扩频信号的频谱结构,因此,置乱后的信号经过快速傅立叶变换(Inverse Fast Fourier Transform,IFFT)后形成的时域信号结构也随之改变,不具备扩频码的周期性,这与后续的仿真结果相吻合,所以该方法提高了信号传输的抗截获性能。由于原始扩频信号的结构被改变,非合作方很难根据盲检测技术检测到信号存在。即便非合作方截获到信号的存在,但在不知道信号置乱规则的情况下,也无法正确解调出原始发送信号。

3 子带置乱与最佳置乱度

3.1 子带置乱

扩频信号的子带置乱过程模拟了图像的Arnold置乱过程。将扩频信号经过FFT后得到的频域数据均匀地划分为N×N个“小频段”,即子带;将这些已经完成分段的信号以子带为单位依次排列成N×N维方阵的形式,并对其依次进行编号,用矩阵的形式表示出信号在置乱之前各个子带的排列规律。 图2表示频带划分以及所有子带排列成N×N维矩阵的示意图。

图2 子带划分示意图Fig.2 Sub-band division diagram

图2中的信号矩阵类似于图像处理中的图像矩阵,并且矩阵中元素的排列存在很强的规律性(原始扩频信号子带排列的规律性)。可以看出,每个元素编号大小变化是有规律的,且相邻元素的编号差值是固定的。即在一行中,左右相邻元素代表原始扩频信号中相邻的频段,编号相差1;在一列中,上下相邻元素的编号之间差值为N,代表两个子带之间相隔N-1个子带。因此,为了打破其规律性,需要对上述信号矩阵进行置乱。采用上节提到的Arnold变换方法,将图2中的N×N维信号矩阵置乱,破坏信号矩阵各元素之间的规律性。即对信号分段FFT值进行置乱,以达到子带置乱的目的。由于Arnold变换具有周期性,因此在一个变换周期内,根据置乱度大小判断最佳置乱次数t,并得到最佳置乱度,然后对信号矩阵进行t次Arnold变换,得到具有最佳置乱度的信号矩阵。

3.2 置乱度

采用Arnold变换将信号矩阵置乱时,进行不同次数的置乱得到的信号矩阵混乱程度不同。根据上节可知,可将信号矩阵视为图像矩阵,不同元素编号表示为不同的灰度级,则衡量信号矩阵的混乱程度,可以借助矩阵灰度来表示。采用以下两种度量方式来描述信号矩阵的混乱程度。

① 衡量混乱程度可以用信号矩阵的方差表示。由于每次变换时信号矩阵不同区域的元素都在改变,因此矩阵元素的分散程度可以采用矩阵的分块方差θ1(t)来衡量[8,16]。② 借助每个元素点与其4邻域元素之间的差值θ2(t)进行衡量[8],即打破矩阵元素编号左右相差1、上下相差N的规律性。

3.2.1θ1(t)的计算

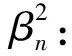
(3)

(4)

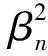
(5)

在一个Arnold变换周期内,对每次变换得到的信号矩阵的方差求平均值,并记为Iavg(β2),设 第t次置乱后信号矩阵的方差为It(β2),则t次变换后信号矩阵的分块方差θ1(t)可以表示为：

(6)

这种方法认为信号矩阵各个分块中的元素编号值与该分块的均值差别越大,信号矩阵变化越剧烈,置乱效果越好。

3.2.2θ2(t)的计算

信号矩阵按照一定顺序排列,矩阵中的元素编号为信号子带的编号,相邻元素(4邻域元素)之间存在关联性,即左右元素编号相差1,则为相邻子带;上下元素编号相差N,则为子带之间的间隔没有改变。为了减小矩阵相邻元素之间的相关性,相邻元素差值越大,矩阵的置乱效果越好,相关性越小说明矩阵的置乱程度越高,因此可以用4邻域差值的方法来衡量矩阵的置乱度。

由于在初始信号矩阵中,上下元素差值固定为N,左右元素差值固定为1。因此,在计算元素的上下邻域差值和左右邻域差值时应分别去掉固定差值N和1的影响。在仿真中将元素编号转换为灰度级,则固定差值可以分别定义为偏差量ε1和ε2。因此,矩阵第x行、第y列的元素值大小用f(x,y)表示,则该点与4邻域元素值的差定义如下：

(7)

式中：ε1和ε2分别表示f(x,y)与上下两个邻域和左右两个邻域的偏差值。f(x,y)与其4邻域元素差值的均值S(x,y)定义如下：

(8)

由式(8)可知,信号矩阵每个元素都对应一个S(x,y)值,因此信号矩阵I的4邻域元素差值的均值可以定义为：

(9)

经过t次Arnold置乱得到的信号矩阵的4邻域差值可以定义为：

(10)

式中：It(S)为第t次Arnold变换得到的信号矩阵I的4邻域元素差值的均值,Iavg(S)为一个置乱周期内的信号矩阵4邻域元素差值的均值。

3.2.3 最佳置乱度

结合上述两种衡量指标θ1(t)、θ2(t),综合度量信号矩阵的置乱度,信号矩阵第t次变换的置乱度可以表示为：

D(t)=λ×θ1(t)+(1-λ)×θ2(t),

(11)

式中：λ为两个指标之间的加权系数,θ1(t)为信号矩阵分块方差,θ2(t)为信号矩阵的4邻域差值。由式(11)可知,置乱度D(t)越大,图像的混乱程度越高。根据不同变换次数t计算出置乱度D(t),经过比较可以得到最佳置乱度,即D(t)的最大值。

4 仿真结果

在Matlab仿真平台上进行了子带置乱仿真,其相关参数设置如下：矩阵阶数N为128,矩阵分块数量L为256,分块矩阵阶数k为8,置乱周期为96次。

在仿真过程中,借用灰度图像的表示方法,得到信号矩阵置乱前的图像表示结果,如图3所示。其中图像的第一个像素点代表信号的第一个子带,最后一个像素点代表信号的最后一个子带,子带的编号大小即图中元素点的颜色深浅。

图3 置乱前各个子带的排列规律Fig.3 Arrangement of each sub-band before scrambling

根据仿真参数可知,图中的子带个数(灰度级)为16 384,其中颜色越深代表灰度值越小,即子带编号越小;颜色越浅代表灰度值越大,即子带编号越大。

根据式(11),将λ分别取1和0,测试θ1(t)和θ2(t)对置乱度D(t)的影响,如图4所示。从图中可知,置乱度与半个变换周期具有一定程度的对称性,对比可知,在一个周期内θ1(t)对置乱度D(t)的影响更加平缓,而θ2(t)的影响曲线则凹凸不平。这是因为θ1(t)反映置乱后矩阵的局部波动特性,在 一个分块矩阵中,每一次置乱的结果虽然不同,但不会引起值的剧烈变化(除两端和中间)。θ2(t)反映置乱后矩阵的细节特征,每一次变化导致各个元素四周的元素值改变,会导致置乱度发生较为剧烈的变化。由对比可知,θ1(t)带来的置乱程度相比于θ2(t)更大,因此在仿真中将权重λ设为大于0.5的数值较为合适(本文λ=0.8)。

(a) λ=1

(b) λ=0

根据子带划分的个数以及Arnold变换的阶数可得变换周期为96次,为了得到一个周期内最佳的置乱次数,仿真得到了置乱次数t与置乱度D(t)的关系如图5所示,可以看出,置乱周期两端的置乱效果最差,置乱83次得到的置乱度是最高的,最佳置乱度D(t)为0.993 3。

图5 置乱次数与置乱度的关系Fig.5 Relation between scrambling frequency and scrambling degree

图6为信号矩阵经过83次Arnold变换后的置乱矩阵,即信号子带乱序排列,可以看出,信号矩阵对应的图像被置乱,即信号子带被打乱分散,与原始扩频信号的子带排列产生了较大的区别,混乱程度高。

图6 子带置乱后的子带排列(83次)Fig.6 Sub-band arrangement after sub-band scrambling (83 times)

为了比较子带置乱过程对扩频系统误码率的影响,在Matlab上进行了相关仿真,仿真条件如下：调制方式为BPSK调制,信号比特速率为1 024 bit/s,扩频序列为8阶m序列,扩频码周期为255,其中 8阶m序列的本原多项式为f(x)=x8+x4+x3+x2+1。通过仿真得到了不同比特信噪比下,有子带置乱过程和无子带置乱过程的系统误码率对比情况如图7所示,可以看出,子带置乱过程几乎不会对系统产生额外的误码影响,同样保持了原始扩频信号低误码率的性能。

图7 误码性能对比Fig.7 BER performance comparison

通信系统采用子带置乱的方法,以提高信号在传输过程中的抗截获性能。为了验证子带置乱方法对信号抗截获性能的影响,采用时延相关[17- 20]的方法判断信号性能好坏。图8仿真结果表明,子带置乱能很好地破坏扩频信号时域的周期特性,进行时延相关检测时,不能得到比较明显的相关峰。相比之下,没有子带置乱的信号有比较明显的相关峰。对于非合作方来说,扩频信号隐藏于噪声之下,并且子带置乱的扩频信号不能依靠其相关峰进行检测,因此很难检测到信号的存在。另外,在知道扩频信号存在子带置乱的情况下,需要知道确切的置乱方法和置乱次数,才能准确恢复信号。

(a) 无置乱

(b) 有置乱

5 抗截获性能分析

由前述仿真结果可知,通过时延相关检测算法,传统的直扩信号周期出现相关峰,而相同的信噪比条件下,置乱后的信号不能检测出明显的相关峰。信号进行时延相关检测后的信号特征主要体现在相关峰值上,同一信号的相关峰一般比其他相关点处的幅值大很多。信噪比越大,相关峰幅值越大,而时延相关后的均值是相对比较小的。因此可以根据时延相关后的峰均比(Peak-to-Average Power Ratio,PAPR)来检测信号。通过设置一定的PAPR门限,时延相关后的PAPR越大越容易被检测到。在不同信噪比条件下仿真计算PAPR,并与不同的PAPR门限进行比较得到有置乱和无置乱两种情况下的检测概率。其中,分别仿真了信噪比为-20 dB和0 dB时,不同PAPR门限下有置乱和无置乱的信号检测概率,如图9所示。

(a) 信噪比为-20 dB

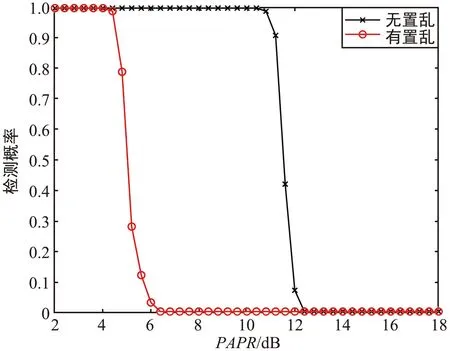
(b) 信噪比为0 dB

从图9(a)中可知,在信噪比为-20 dB、PAPR设定为4～8 dB的情况下,有置乱的信号相比于无置乱的信号检测概率更低;在图9(b)中,有置乱的信号检测概率同样比无置乱的信号检测概率更低。由图9可得,信噪比增大,两条曲线往右平移,即对应更高的PAPR门限。并且无置乱曲线平移量更大,有置乱的曲线平移量更小,说明有置乱的信号随着信噪比的增加,被检测到的概率增加更缓慢。因此,有置乱的信号具有更好的抗截获性能。

从信噪比和PAPR门限两个维度上整体分析两种信号的检测概率。仿真条件设置为：信噪比-40～10 dB,PAPR门限值3～18 dB,仿真结果如图10所示,可以看出,在不同信噪比和PAPR条件下,信号在有置乱的情况下检测概率低于无置乱的情况。说明该置乱方法提高了信号的抗检测能力,这正是该方法相比于传统扩频信号的优势,符合该方法的预期结果。在相同信噪比条件下,两种仿真结果的检测概率都是随着PAPR门限值的增大而减小,因为门限值越低,仿真结果超过门限的可能性越大,反之可能性越小;在相同PAPR门限条件下,检测概率随着信噪比的增大而增大,因为信噪比越大,噪声的幅值越小,信号的峰值越大,因此仿真的PAPR值会越大,更易超过PAPR门限值,检测概率增大。综上所述,该方法相比于传统的扩频信号抗截获性能提升,有继续研究的价值。

图10 有置乱和无置乱情况下检测概率Fig.10 Detection probability with and without scrambling

6 结束语

使用图像加密处理方法中的Arnold变换,将发送端的扩频信号在频域上进行置乱,再经过IFFT转为时域信号后进行发送传输。接收端对接收信号进行解置乱,再进行常规的解调和解扩,恢复出包含重要信息的有用信号。经过置乱的信号采用时延相关法检验其信号特征,与扩频信号相比,置乱破环了传统扩频信号的周期性,有一定的抗截获效果。采用基于PAPR的判决检测方法,仿真了有、无置乱两种情况下信号在不同PAPR门限、不同信噪比条件下的检测概率。在相同条件下,置乱信号的检测概率低于传统扩频信号,提高了信号的抗截获性能。