Kriging水动力学代理模型在水库群优化调度中的应用

2024-02-21徐杨,吕昊,刘帅,方威,覃晖

长江科学院院报 2024年2期

徐杨,吕昊,刘帅,方威,覃晖

(1.三峡水利枢纽梯级调度通信中心,湖北宜昌 443000; 2.中国电建集团华东勘测设计研究院有限公司,杭州 311122;3.华中科技大学土木与水利工程学院,武汉 430074; 4.华中科技大学数字流域科学与技术湖北省重点实验室,武汉 430074)

0 引言

长江是我国第一大河,蕴含着丰富的水能资源,尤其在金沙江下游河段,具有水量大且落差集中的天然优势。近年来,随着金沙江下游—三峡梯级水库群的相继投产运行,水库群所承担的防洪、发电、生态等综合任务也愈加繁重[1-2]。

为此,如何科学制定水库群调度运行方案以提高流域水资源利用率、提升电站安全运行水平、修复和改善自然生态环境并充分发挥流域航运等效益已成为现阶段亟待解决的科学难题[3-4]。20世纪60年代以来,随着越来越多控制性水库陆续建成并投产,调度决策者开始综合考虑梯级水库的整体效益以及防洪、兴利、生态等目标之间的影响[5]。水库优化调度研究从早期单库单目标向梯级水库群多目标联合优化调度方向不断深入并建立了一系列方法体系和风险决策理论[6]。然而传统的水库调度模型需要在目标量化过程中对水位、流量等水力学要素进行时段均化处理,缺少对水流动态过程的考虑,引入水动力学模型有助于实现目标的精确量化,但优化求解过程需要频繁调用水动力学模型,计算成本过高,难以直接与调度模型嵌套[7]。使用代理模型近似替代数值仿真模型在水文模型和地下水模拟模型中已解决了诸多优化难题[8- 9],但在水库调度优化中仍鲜有应用和研究。Kriging模型是最具代表性的代理模型之一,它能够通过空间建模和数据插值来映射水文随机过程中变量之间的相关关系。为此本研究拟采用最具代表性的Kriging代理模型代替长耗时水动力学模型。

本文以金沙江下游—三峡六座梯级水库群作为研究对象,建立了梯级水库群生态、航运和发电多目标调度模型并引入基于水动力学的Kriging代理模型[10-11]精确量化电站之间河流演进过程,采用多目标优化方法进行求解并采用投影追踪法对得到的帕累托前沿进行排序决策。实例结果表明,Kriging代理模型表征了多目标之间的博弈关系同时提高了计算效率,能够为梯级水库精细化调度提供技术支撑。

1 水库群多目标优化调度建模及求解

1.1 基于水动力学的Kriging模型构建

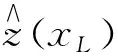
(1)

(2)

式中:λα为基于最小估计方差规则确定的第α个观测点处的加权系数,服从标准化条件;xα为第α个观测点位置。

平面二维水动力模型使用MIKE21 FM模块[13-14]搭建,采用无结构三角形网络,忽略水体垂向上的流动差异性,计算求得的流速值为沿水深方向积分所得的平均值。模型控制方程为基于不可压缩流体和雷诺数平均化假设的Navier-Stokes方程,忽略密度变化对流体性质的影响。二维水动力控制方程组如下所示:

(3)

(4)

(5)

(6)

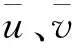
针对长耗时水动力学模型难以与优化调度模型嵌套高效求解的问题,本文基于水动力学模拟结果,通过构建Kriging代理模型模拟长耗时水动力学模型,进一步将构建的Kriging代理模型与流域水库群多目标调度模型耦合,以提高模型计算效率同时保证精确性。

1.2 水库群多目标精细化调度模型构建

1.2.1 目标函数

水库群多目标精细化调度模型[15]采用总发电量最大、生态适宜度最大、航运适宜度最大作为优化目标,表达式如下所示。

(1)发电目标F1为

(7)

(2)生态目标F2为

(8)

式中:DES为研究区域的生态适宜度;ESi为物种的生态适宜度;n为物种数目。

(3)航运目标F3为

F3=max DNS=

(9)

式中:DNS为某一调度工况下的航运适宜度;NSmain,i、NSnav,i分别为主航道区、通航关键区单元内的适宜度值;Ai为第i个计算单元的面积;M、N分别为主航道区、通航关键区单元数。

1.2.2 约束条件

(1)水位约束。水位约束取水库最低、最高水位和调度期设定水位约束的交集,即

(10)

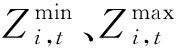
(2)下泄流量约束。下泄流量最大值取电站最大下泄能力约束以及在调度期内生态和航运对下泄流量约束的交集;最小值取水库对应下游河段生态基流和最低通航流量中的较大值,即

(11)

(12)

(3)出力约束。取电站保证出力与电站最大出力的交集,同时还需满足发电保证率不低于95%的要求,即:

(13)

(14)

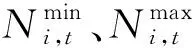
(4)水量平衡约束。式(15)表示某一水库不同时段的平衡关系,式(16)表示梯级水库间的水力联系。

Vi,t+1=Vi,t+(Ii,t-Qi,t)Δt;

(15)

Ii,t=Qi-1,t-τi-1+qi,t。

(16)

式中:Vi,t、Vi,t+1分别为第i个水库第t时段和第t+1时段的库容;Ii,t为第i个水库第t时段的总入流量;qi,t为梯级水库区间入流量。

1.3 求解方法

水库群多目标精细化调度包括多个复杂约束,属于典型的非线性、多时段、强耦合[16]的数学优化问题。在求解过程中,基于生物进化机制建立的多目标进化算法[17]通过随机生成初始种群,模仿进化过程对种群进行选择、交叉和变异处理,然后通过种群的不断进化迭代方式,最终得到一个高适应度的种群作为非劣解集。

1.3.1 求解算法及约束处理规则

(1)求解算法。本文的水库群多目标调度模型采用由Deb等提出的NSGA-II算法进行求解[18]。该算法求解结果具有较好的收敛性和分布性,可用于解决实际调度问题。算法参数设置:种群规模为100,交叉率为0.9,变异率为0.014,交叉分布指数和变异分布指数均为20,最大迭代次数300 000。

(2)编码方式。为了有效求解多目标优化调度模型,以各电站坝前水位作为决策变量进行编码,编码为

Xi={Z1,1,…,Z1,T,…,Zi,1,…,Zi,t,…,

Zi,T,…,Z6,1,…,Z6,T} 。

(17)

式中:Xi表示种群中个体位置向量;Zi,t表示第i个水库第t个时段的坝前水位值;T表示调度周期。

(3)约束处理方式。如果种群中个体违反约束限制,按照如下规则进行选择[19]:①在不违背约束的情况下,根据目标函数值的优劣,确定个体间支配关系;②当有违反约束个体与未违反约束个体比较时,选择未违反约束个体;③当两个体均违反约束时,选择违反约束程度较小的个体。

1.3.2 基于Kriging模型的多目标调度模型求解框架

通过Kriging代理模型建立水库下泄流量过程-关键河段水力学要素-调度目标适宜度的映射关系。在求解模型前,使用水动力学模型计算不同调度工况下的水力要素时空分布,基于数值模拟结果计算不同调度工况下的生态适宜度和航运适宜度,并以此作为样本集训练代理模型,分别建立下泄流量过程与生态适宜度和航运适宜度之间的映射关系。在调度模型求解过程中,水库下泄流量过程作为代理模型的输入量,代理模型输出的目标适宜度作为算法中个体的评价指标并参与目标评价,从而减少水动力学模型调用次数,降低模型求解成本,实现了代理模型与流域水库群多目标优化调度模型的耦合,有效提高了水库群多目标调度模型的求解效率。

基于Kriging模型的水库群多目标精细化调度模型算法求解框架如图1所示。

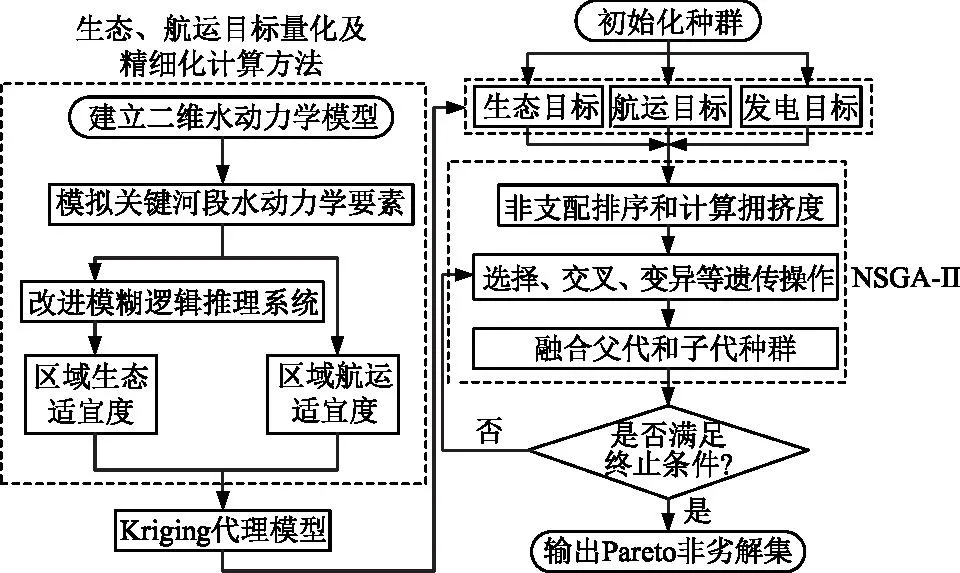
图1 水库群多目标优化调度求解框架Fig.1 Framework of multi-objective optimal scheduling for multi-reservoir

其步骤如下:

Step1:构建关键河道水动力学模型,根据调度工况计算区域内各水力要素分布。

Step2:根据水动力学模型模拟结果,根据式(8)按照生态目标的量化评价方法[20]计算中华鲟及四大家鱼产卵的生态适宜度,依式(9)参照I级航道标准计算航运适宜度。

Step3:建立基于水动力学的Kriging代理模型,模拟不同调度工况与生态适宜度和航运适宜度之间的映射关系。

Step4:初始化NSGA-II算法参数,根据多目标调度模型目标及约束要求,生成初始种群。

Step5:根据式(7)计算个体的发电目标适宜度值,基于Step3中构建的Kriging代理模型,分别计算个体的生态目标适宜度值和航运目标适宜度值。

Step6:根据Step4中的参数设置,对初代父代种群个体进行选择、交叉及变异等遗传操作,获得子代种群。

Step7:合并父代种群和子代种群,并进行非支配排序,根据精英策略,生成下一代父代种群,利用拥挤度排序法,确保种群个体在该非支配层上分布的均匀性,避免个体过度聚集,保证种群多样性。

Step8:通过种群的不断进化迭代直至满足算法终止条件,输出最终的Pareto非劣解集。

2 应用算例及分析

2.1 工程背景

选取金沙江下游六座梯级水库,分别为乌东德、白鹤滩、溪洛渡、向家坝、三峡和葛洲坝大型水利枢纽工程作为研究对象。确定生态关键河段为葛洲坝下游产卵场和宜都产卵场,综合考虑调度过程对中华鲟及四大家鱼产卵活动的影响;确定通航关键河段为葛洲坝至宜昌九码头河段、磨盘溪至云池河段,考虑引航道、航道分汊段、码头前沿停泊水域及主航道航行条件与水流动态过程间的响应关系,以葛洲坝下游河段作为水动力学及代理模型模拟范围[21- 22]。各水库间拓扑关系如图2所示。由于生态需水具有较强季节性,故生态效益考虑宜都产卵场四大家鱼5月份、6月份的产卵期,葛洲坝坝下河段中华鲟10月份、11月份的产卵期。采用2019—2020年长江径流数据资料进行调度模拟。

图2 金沙江下游梯级水库拓扑关系图Fig.2 Topology diagram of cascade reservoirs in the downstream of Jinsha River

2.2 耦合模型求解能力分析

基于不同调度工况,建立Kriging代理模型的训练集,分别采用表1给出的5种变异函数模型进行训练,给定初始参数设置,并按照残差平方和最小标准确定变异函数模型参数,将训练好的代理模型与水动力学模型模拟结果进行对比检验,比较使用不同变异函数的Kriging模型预测精度,比较结果如表2和表3所示。表中加粗的模型是较为理想的模型。

表1 变异函数模型Table 1 Variogram models

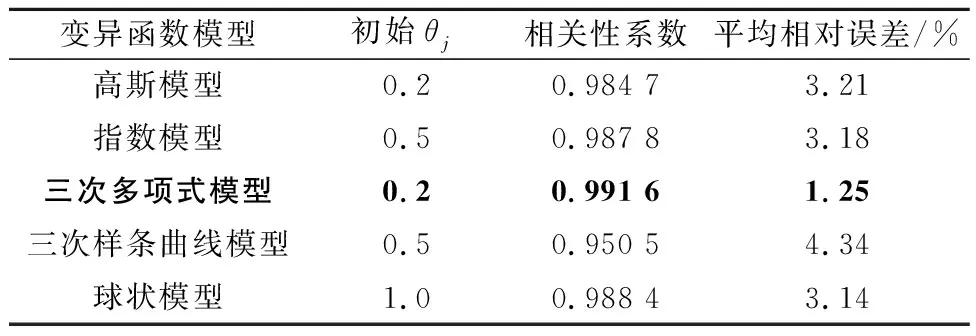
表2 生态代理模型变异函数比较结果Table 2 Comparison of variation function among ecological surrogate models

表3 航运代理模型变异函数比较结果Table 3 Comparison of variation function among shipping surrogate models

根据验证结果可以看出,生态目标评价代理模型的变异函数选用三次多项式模型,相关性系数为0.99,平均相对误差为1.25%,最大相对误差≤5%;航运目标评价代理模型的变异函数选用指数模型,相关性系数为0.98,平均相对误差为1.31%,最大相对误差不超过5%。耦合调度模型单次运行耗费机时110 s,明显少于传统水动力学模拟耗费机时48 min。

2.3 多目标调度方案分析

选取金沙江下游—三峡梯级2019—2020年的径流数据资料,采用NSGA-II进行求解,以乌东德水库入库流量及各区间流量作为初始入流条件,综合考虑各种边界条件得到两两目标的帕累托前沿。

根据图3和图4可知,三个目标中的两两目标之间具有竞争关系,这表明发电、航运和生态目标三者具有竞争关系。其中,在2019年来水条件下,生态目标与发电目标的帕累托前沿为弧形,生态适宜度的下降趋势起初较为平缓,总发电量>3 350亿kW·h时,下降斜率逐渐变大,提升单位总发电量对流域生态造成的负面影响愈加严重。在2020年来水条件下,生态目标与发电目标的帕累托前沿较为顺直,总发电量增加对生态环境的负面影响相对稳定。进一步可以看出生态目标与航运目标存在较为明显的竞争关系,生态适宜度的提高在一定程度上会导致航运适宜度的降低。当生态适宜度<0.6时,生态目标与航运目标间难以观察到明确的帕累托前沿;当生态适宜度>0.6时,航运适宜度随生态适宜度的升高而明显下降,且斜率也越来越大,弧形帕累托前沿较为清晰。而发电目标与航运目标间的竞争关系较弱,两目标间帕累托前沿关系较模糊。

图3 2019年梯级水库帕累托前沿Fig.3 Pareto front for cascade reservoirs in 2019

图4 2020年金沙江下游—三峡梯级帕累托前沿Fig.4 Pareto front for cascade reservoirs from lower Jinsha River to Three Gorges in 2020

2.4 子目标最优方案分析

选取2020年金沙江下游—三峡梯级六库来水过程作为输入,得到100个多目标非劣解方案结果,按全年总发电量从高到低排序。从中选取生态效益最大、航运效益最大和发电效益最大3个最优方案进行对比分析。

根据图5分析可得,生态适宜度对不同优化调度方案的敏感度较高,航运适宜度和梯级总发电量对不同优化调度方案的敏感度较小。对比生态效益最大、航运效益最大和发电效益最大这3个优化调度方案,生态效益最大方案在生态适宜度方面均明显高于其他两方案,体现了生态目标与航运目标、发电目标间明显的竞争关系,发电调度对流量过程的改变在一定程度上满足了中华鲟和四大家鱼对水流条件的部分要求,因而发电效益最大方案的生态适宜度比航运效益最大方案的生态适宜度更高。航运方面,不同调度方案间的航运适宜度差异不大,但不同月份间差异较为明显,枯水期(1—3月份)和洪水期(7—9月份)的航运适宜度普遍偏低,符合内河船舶安全航行对航道内水量不宜过大和过小的要求;发电方面,各调度方案均呈现下半年发电量明显高于下半年发电量的特点,总体变化趋势与年径流过程相似。

图5 各子目标最优方案对比Fig.5 Comparison of optimal solution among sub-objectives

2.5 多目标优化调度方案决策

流域水库群不仅具有防洪、发电等基本功能,还承担着对生态、灌溉、供水和航运等方面的保障任务[23],但各任务之间往往存在竞争关系且难以用统一标准进行比较,为此本文通过投影追踪法[24]对所得到的优化调度方案进行优选排序,投影追踪法可通过把高维数据投影到低维子空间,并根据特征投影在低维空间内,能够较好地处理和分析高维数据,具有准确度高,抗干扰性和稳健性的优势[25]。

本节将2020年得到的帕累托前沿进行优化排序,将3个指标值代入投影追踪聚类模型计算,其中n=100,p=3,经模型计算最优投影方向向量为a*=(0.222,0.755,0.617),计算各方案响应的投影值,排序前5名方案的结果如表4所示。计算得到生态-航运-发电多目标优化方案前5优选排序结果(“方案A>方案B”表示“方案A优于方案B”)为方案47>方案62>方案61>方案56>方案59。