嵌入Cat映射的混合变异探路者算法及其应用
2024-02-21毛雪迪夏煌智张鲁平李永超
毛雪迪,王 冰,夏煌智,张鲁平,李永超
(牡丹江师范学院 数学科学学院,黑龙江 牡丹江 157000)
0 引 言
智能优化算法是一类基于自然界生物进化、群体智能、神经网络等理论和方法而发展起来的优化算法,这类算法通过模拟生物进化、群体社会行为等机制寻找最优解或次优解,具有全局优化、鲁棒性强等特点,在许多领域中得到了广泛应用。2019年,Yapici等人提出了一种新的群智能优化算法,即探路者算法(Pathfinder Algorithm,PFA)[1],它基于生物进化理论和群体智能原理,通过模拟生物进化和自然选择的过程寻找最优解。该算法具有自适应参数设置、多种探索策略、鲁棒性强和高效性等特点,已经在多个领域得到了广泛的应用,如机器学习、信号处理、图像处理等,然而,PFA也存在收敛速度慢、求解精度不高、容易陷入局部最优等问题。文献[2]通过借助PFA中探路者与跟随者独特的更新模式,成功地提升了灰狼优化算法的寻优性能,这种融合方式得到的优化算法具有较高的收敛精度。文献[3]在PFA中引入了一种向导机制,使得带有向导机制的探路者个体能够收集周围个体的优良信息,并将这些信息传播给其它个体,同时,还引入了一种新型的变异概率pcR,以增强算法跳出局部最优的能力。文献[4]将教与学算法与PFA相结合,通过在跟随者阶段中引入指数步长算子优化跟随者个体提高了算法整体的寻优精度和收敛速度。文献[5]利用动态反向学习策略提升了初始种群质量,提出一种新的跃迁档案保存并创造新的最优个体,引导陷入局部最优的个体跳出当前位置;又提出一种双跳模型协调算法的全局搜索和局部开发能力。
为解决上述问题,该文提出一种嵌入Cat映射的混合变异探路者算法(CHMPFA)。首先,利用混沌反向学习策略增加了初始种群的多样性和分散性;其次,在探路者更新公式中加入衰减因子,在迭代过程中控制探路者的搜索步长从而控制搜索范围;然后,利用随机数对最优个体进行混合变异,帮助其脱离当前区域向全局最优值靠近;最后,通过在10个基准函数和12个CEC2017基准测试函数进行仿真实验验证策略的鲁棒性,并将CHMPFA应用于压力容器工程问题中,优秀的寻优结果进一步证明了改进算法的有效性。
1 标准探路者算法
在标准探路者算法中,种群只分为两种类型:探路者和领导者,探路者为适应度值最好的个体,其余个体为跟随者的角色。
探路者算法中的位置向量X将由N个维度为d的种群个体组成,每个个体定义为Xi=[xi1,xi2,…,xid],各维度的上界为ub=[ub1,ub2,…,ubd],下界为lb=[lb1,lb2,…,lbd],即种群随机初始化为:
XN×d=rand(N,d)×(ub-lb)+lb
(1)
其中,N为种群规模,d为空间维度;在种群迭代过程中,选出适应度值最优的个体作为探路者,跟随者均向它移动,更新方式为式2:
(2)
(3)

探路者更新完后,跟随者根据探路者位置进行更新,更新方式为式4:
(4)
(5)
Dij=‖xi-xj‖
(6)
R1=αr2
(7)
R2=βr3
(8)
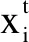
2 算法改进
2.1 混沌反向学习初始化种群
为了改善种群质量和提高算法的搜索性能,该文引入Cat混沌映射结合反向学习的方法[6]初始化种群。Cat映射是一个结构简单的二维可逆混沌映射,可以产生具有随机性、分散性和复杂性的种群分布,能够帮助算法从多个起点同时进行搜索,增加算法的全局搜索能力,其表达公式如下:
(9)
反向学习[7]则是一种基于贪心策略的启发式算法,可以在有限的时间内快速生成优秀的种群,增加算法的局部搜索能力。将两种方法结合起来使用,能够在初始化种群时既考虑全局性又考虑局部性,提高算法的搜索效率和多样性。此外,Cat混沌映射和反向学习还可以互相补充彼此的不足。Cat混沌映射在产生种群时具有一定的随机性,容易产生多样性,但可能会受到局部最优解的影响,难以快速收敛;而反向学习虽然可以快速生成优秀的种群,但可能会陷入局部最优解,将两种方法结合使用可以平衡二者之间的优缺点,提高算法的搜索性能和鲁棒性。
由混沌序列结合反向学习初始化种群,其步骤是:首先利用Cat映射产生初始种群xi(i=1,2,…,N),然后为每个初始解按公式10求其相应的反向解。
(10)
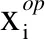
2.2 赋予衰减性的探路者更新方式
为解决探路者算法搜索效率和求解精度低等问题,该文提出将衰减因子引入PFA探路者更新公式中,随着迭代的进程不断降低衰减因子的大小,算法搜索空间的范围也会逐渐缩小至最优解附近,从而避免了算法过早陷入局部最优区域的状况,这能够使算法快且准地找到理论最优解,帮助算法改善了搜索效率和求解精度。提出的衰减因子是一个非线性递减函数,定义式如下:
(11)
其中,s∈[0,1]为衰减系数(该文选取s=0.5),控制算法收敛速度,t为当前迭代次数。引入衰减因子后的探路者更新公式如下:
(12)
通过衰减因子的非线性变化,使算法在不同阶段的搜索更加高效。在算法初期,较大的衰减因子帮助探路者在解空间中进行更广泛的搜索;随着算法的迭代,较小的衰减因子帮助算法对局部区域进行更加精确的探索。
2.3 混合变异策略
(1)柯西变异。
柯西变异来源于柯西分布[8],一维柯西概率密度公式如下:
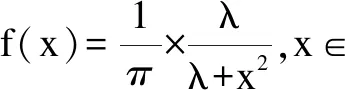
(13)
当λ=1时,是标准柯西分布。从图1的标准柯西、高斯分布概率密度函数曲线观察可知,柯西分布与高斯分布类似,主要差异表现为柯西分布峰值略小于高斯分布,柯西分布在原点处有较高的概率密度,在两端有较低的概率密度,柯西分布的边缘较长且扁平,比高斯分布更平缓的逼近于0。
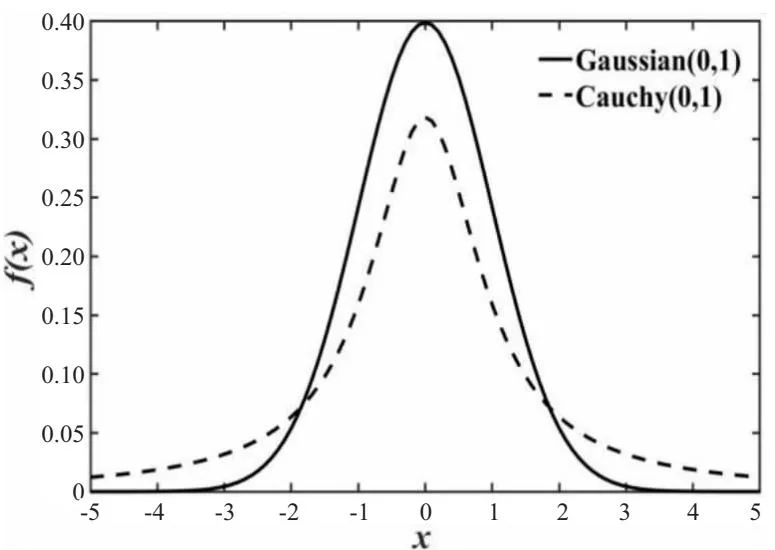
图1 标准柯西、高斯分布概率密度函数曲线
根据此特点对探路者和跟随者位置更新后的最优个体进行柯西变异,通过柯西算子的扰动特性提升算法的寻优性能。当最优个体无法跳出局部最优解时,柯西算子能够提供较长的步长帮助其个体跳出局部最优;当最优个体向理论最优值靠近时,柯西算子能够提供较短的步长提升个体收敛速度。柯西变异策略数学模型如下:
(14)
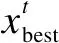
(2)高斯变异。
高斯算子可以防止种群陷入局部最优,增加种群的多样性。为了提升PFA局部搜索的能力和跳出局部最优的概率,对最优个体进行高斯变异操作,高斯概率密度公式和高斯变异策略数学模型如下:
(15)
(16)
其中,μ表示期望,σ表示标准差,标准正态分布的期望和方差分别设置为0和1,Gaussian(σ)是由式15形成的标准正态分布的随机变量。
由图1可知高斯分布的概率密度函数呈现钟形曲线,均值即为期望值,并且其方差较大、分布范围较广,所以当最优个体处于局部最优解时,高斯变异可以让其位置发生微小变化,使得搜索过程可以继续向周围未被探索的区域扩展,从而增加逃离局部最优的可能性。
(3)混合变异。
在PFA中引入柯西变异和高斯变异可以使得算法更加全面地探索解空间,从而有更大的可能找到最优解。柯西变异可以增加算法的全局搜索能力,因为它具有长尾分布,可以探索到远离当前搜索点的区域;而高斯变异则可以增加算法的局部搜索能力,因为它可以更加精准地探索周围区域,从而更容易找到局部最优解。所以,该文根据变异概率p将柯西变异和高斯变异融合为混合变异策略引入PFA当中,如公式17所示:
(17)
但是,变异后最优个体位置无法保证优于原始位置,所以在混合变异位置扰动后加入保优策略,即贪婪策略,通过比较变异后最优个体与原最优个体的适应度值,选取适应度值最好的个体作为当前代的全局最优解,则把变异后个体替换掉原始个体,判断公式如下:
(18)
2.4 CHMPFA算法伪代码
CHMPFA算法伪代码如下:
Initialize PFA parameters
Initialize population using chaoticopposition-based learning
Calculate the fitness of initial population
Find the pathfinder
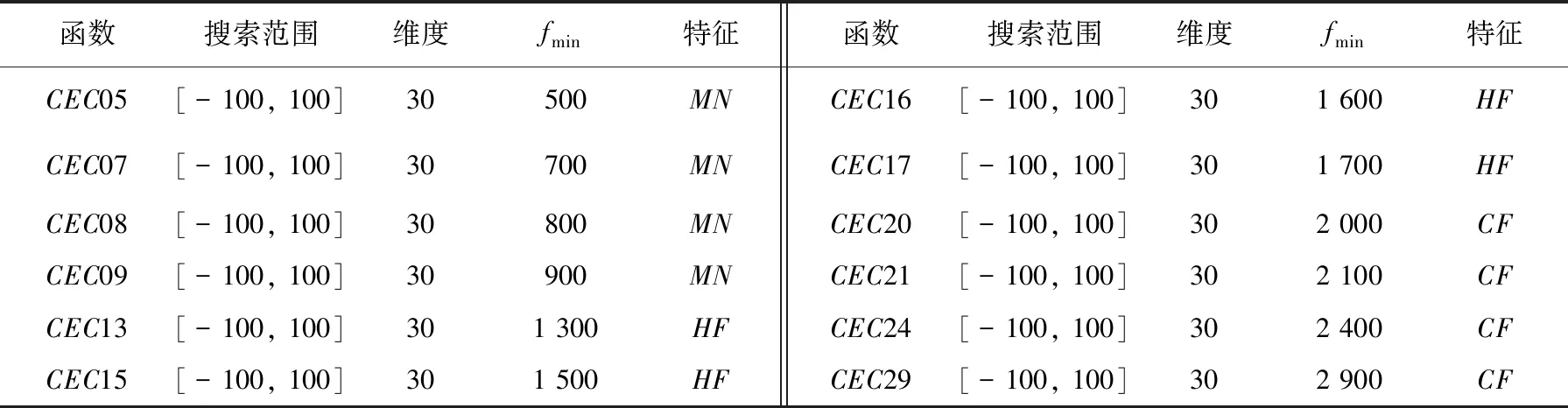
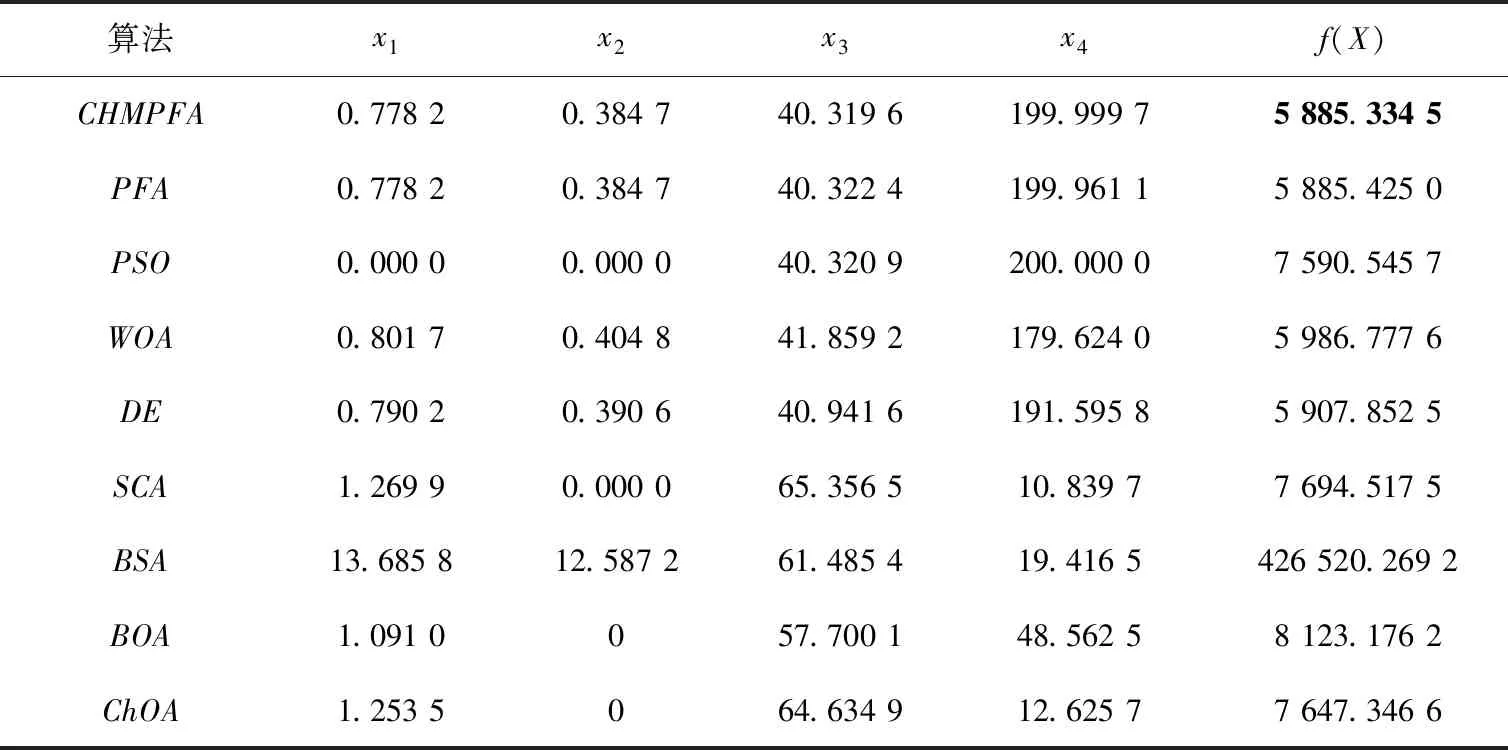
Whilet Update pathfinder the position using Eq.(12) and check the bound if new pathfinder is better than old Update pathfinder end fori=2 to maximum number of populations Update follower the position using Eq.(4) and check the bound end Calculate new fitness of members Find the best fitness if rand<0.5 Update best number position using Eq.(14) else Update best number position using Eq.(16) end Calculate the fitness of new best number if new best fitness Update best nember end Calculate new fitness of members Find the best fitness if best fitness Pathfinder = best member Fitness = best fitness end t=t+1; end Whil 时间复杂度是体现算法运行效率的重要指标,现假设种群规模为N,空间维度为d,最大迭代次数为Tmax,f(x)表示适应度函数。根据标准PFA流程可知,PFA的总时间复杂度为O(d+f(d)),现对CHMPFA的时间复杂度进行分析。 对于CHMPFA,在初始化种群阶段,假设初始化算法参数的时间为t1,按适应度值对所有个体进行排序并选定探路者的时间为t2,由于通过混沌反向学习初始化种群个体的时间复杂度为O(N×d),且对每个个体计算适应度值的时间为f(d),则初始化种群阶段的时间复杂度为: T1=O(t1+N×f(d)+t2)+O(N×d)= O(d+f(d)) 进入迭代期,在探路者阶段,探路者数目为1,假设计算自适应权重w的时间为t3,生成随机数r1需要的时间为t4,计算A的时间为t5,更新探路者位置时间为t6,对探路者个体的每一维边界处理的时间为t7,则探路者阶段的时间复杂度为: T2=O(t3+1×(t4+t5+t6+t7)×d)=O(d) 在跟随者阶段,CHMPFA更新跟随者位置的方式与标准PFA保持一致,所耗费的时间并没有增加。因此,跟随者阶段的时间复杂度也应与标准PFA一致为: T3=O(d+f(d)) 在变异阶段,最优个体进行柯西变异或高斯变异的时间为t12,计算最优个体适应度值的时间为f(d),利用贪婪策略判断新最优个体是否代替旧最优个体的时间为t13,保留最优个体位置的时间为t14,对最优个体的每一维边界处理的时间为t15,则变异阶段的时间复杂度为: T4=O(1×d×(t12+t13+t15)+t14+1×f(d))=O(d+f(d)) 综上所述,CHMPFA的总时间复杂度为T=T1+Tmax(T2+T3+T4)=O(d+f(d))。因此,CHMPFA的时间复杂度与标准PFA一致,执行效率并未下降。 为测试CHMPFA的性能,将CHMPFA与PSO[9],DE[10],WOA[11],BSA[12],SCA[13],ChOA[14],BOA[15]以及标准PFA[1]在10个基准测试函数(函数信息如表1所示)上进行30次独立实验,其中f1~f5为单峰函数(UN),有唯一的全局最优解,目的是检验算法的寻优能力和收敛速度;f6~f10为多峰函数(MN),有较多的局部最优解,目的是验证算法跳出局部最优和避免过早收敛的能力。 表1 基准测试函数 为了实验的公正性,所有算法均在Intel(R) Core(TM) i5—11260H CPU@2.60 GHz,Windows 10系统,16 GB内存,64位操作系统的计算机上进行寻优测试,通过MATLAB R2021a软件进行仿真实验。统一设置实验种群规模N为30,实验最大迭代次数Tmax为1 000,每个算法在各基准测试函数上进行30次独立实验,将实验得到的平均值(Mean)与标准差(S.D)数据进行统计,实验参数如表2所示。 表2 各算法实验参数 实验一:从表3记录的10个基准测试函数实验结果得知,相对于其余8种算法,该文改进的CHMPFA均有着最小的平均值与标准差。 表3 基准测试函数寻优结果对比 从寻优精度角度观察,CHMPFA在各个基准测试函数上均取得了最小的平均值,且在4个单峰函数(f1,f2,f3,f4)与2个多峰函数(f8,f9)上找到了理论最优值0。其原因是由于CHMPFA在初始化种群阶段引入了混沌反向学习策略,使得初始种群在解空间中分布得更加均匀,为后续的优化过程奠定了良好的基础,有助于避免种群陷入局部最优值附近,从而增加全局搜索的可能性;在迭代前期,探路者更新步长较大,可以全面搜索整个解空间,以探索更广泛的解空间,提高算法的全局搜索性能,在迭代后期,探路者更新步长逐渐减小,从而更加注重对局部解空间的探索,以期发现局部最优解;当算法陷入局部最优值时,CHMPFA以一定的变异概率进行柯西变异或者高斯变异使算法跳出局部最优值所在区域,这样的随机性引入可以有效地增加算法的搜索广度,避免算法过度依赖局部搜索,从而提高了算法的全局搜索能力,最终搜索到理论最优值。 从寻优稳定性角度观察,在函数f10上,CHMPFA的标准差仅次于WOA的标准差,但在其余9个基准测试函数上均取得了最小的标准差,表明CHMPFA在保证寻优精度最高的同时寻优稳定性也处于较高水平。 实验二:为了进一步评估CHMPFA的表现,通过Wilcoxon秩和检验[16]来验证与其它算法之间是否存在显著的差异。该文选择0.05作为显著性水平进行Wilcoxon秩和检验,如果CHMPFA优于对比算法,则p-value<0.05;如果CHMPFA与对比算法相当,则在数据中记录为NaN;如果CHMPFA劣于对比算法,则p-value≥0.05,并且将这些数据以黑体表示。该文使用“+/=/-”符号来表示CHMPFA“优于/相当于/劣于”对比算法。 根据表3的实验结果可知,CHMPFA与标准PFA在9个基准测试函数上得到的p值远小于显著性水平0.05,表明CHMPFA在寻优性能上优于标准PFA,这是因为CHMPFA集成了混沌反向学习初始化种群策略、赋予衰减性探路者更新方式和混合变异策略,Cat混沌映射结合反向学习可以在初始阶段就引导种群朝着全局优势方向进行搜索,从而提高算法的全局优化性能;衰减因子帮助算法逐渐收敛到最优解附近,提高算法的稳定性和可靠性;对最优个体进行变异提高了算法跳出局部最优的概率,便于找到全局最优解。除探路者算法本身之外,CHMPFA与除WOA外的6种算法在10个基准测试函数上得到的p值同样远小于显著性水平0.05,说明CHMPFA较以上6种算法也有着更加优秀的寻优性能;而对于WOA,即使存在着与CHMPFA性能相当或较劣的现象,但也是少数情况,从整体算法性能看来,CHMPFA仍占据显著优势。 实验三:基于10个基准测试函数的平均绝对误差(Mean Absolute Error,MAE),将所有算法的性能定量分析后进行排序,是评估算法有效性与可行性的可靠方法[17]。计算得到的MAE越小表示算法的平均结果与理论最优结果的绝对误差和越小,算法性能越优秀,其计算公式为: (19) 其中,avg_Bi表示算法得到的全局最优解的平均值,∂i表示选取基准测试函数的理论最优值,Lf表示选取基准测试函数的个数。实验结果显示,CHMPFA的MAE的排名第一,进一步验证了改进算法的鲁棒性。 所有算法对函数求解寻优时的收敛曲线如图2所示(选取部分函数f2,f5,f6,f8和f9),为了方便观察曲线的收敛情况,对纵坐标取10为底的对数。 (a)f2收敛曲线 (b)f5收敛曲线 (c)f6收敛曲线 (d)f8收敛曲线 (e)f9收敛曲线 由图2可知,CHMPFA在迭代前期收敛曲线下降较快,这是由于PFA初始阶段的种群由混沌反向学习策略生成,相较于随机生成种群,Cat映射生成的种群遍布整个搜索空间,再通过反向学习策略,增加种群多样性的同时减少了个体重叠现象,更有利于探路者和跟随者的位置更新。 在图2(a)和图2(b)的单峰函数图像中,CHMPFA在f2函数上收敛速度较快,其余8种算法在寻优性能上较弱于CHMPFA;对于函数f5,虽然在迭代结束时9种算法均未能找到理论最优值,但是CHMPFA的寻优精度相对较高,收敛曲线有持续下降的趋势,这是由于衰减因子为探路者在迭代后期缩减探索范围,使探路者带领跟随者在局部区域能够更加精密的探索,不断地向最优解区域靠近,最终使得CHMPF在寻优精度上优于其它算法。 在图2(c)~(e)的多峰函数图像中,CHMPFA在f9函数上50次迭代内就找到了理论最优值0,而除WOA外其余7种算法均出现了不同程度的停滞现象,这是由于在PFA中加入了变异和贪婪选择策略,以一定的概率选择高斯变异或者柯西变异的最优个体增强了跳出局部最优的能力,该策略在CHMPFA寻优过程中发挥着重要的作用;在函数f6和f8上,虽然所有算法均没有跳出局部区域,但结合表3可知,CHMPFA的迭代曲线收敛速最快,在寻优精度上远超其它所对比的算法。 综上所述,无论在单峰函数还是多峰函数,在每个函数上CHMPFA的寻优精度和收敛速度都十分出色,验证了综合三个改进策略CHMPFA的优化效果。 为了进一步评估CHMPFA的鲁棒性,在CEC2017基准函数中选取部分多峰函数、混合函数(Hybrid Function,HF)与复合函数(Composition Function,CF)进行求解寻优,选取的函数如表4所示。设置初始种群规模为30,最大迭代次数为1 000,维度为30,各算法运行30次的平均值(Mean)与标准差(S.D)记录在表5中。 表4 CEC2017基准测试函数 表5 CEC2017基准测试函数寻优结果对比 根据表5可知,CHMPFA在12个CEC2017基准测试函数上寻优所得的平均值和标准差均比其余算法的优,这是由于CHMPFA引入了混沌反向学习策略,赋予种群更深层次的多样性,使初始种群不再随机地遍布于搜索空间;并将衰减因子引入探路者公式中,帮助探路者更快地遍历解空间,通过逐渐减小搜索步长从而加深对局部区域的开采,提高了找到全局最优解的概率;由于CEC2017函数局部极值众多,所以混合变异策略在CHMPFA寻优过程中发挥着重要的作用,使算法能够跳出局部极值向函数理论最优值靠近。 压力容器设计问题的目标是使各项费用总和最低。这一模型有4个决策变量:筒体厚度Ts(0≤x1≤99)、封头厚度Th(0≤x2≤99)、筒体半径R(0≤x3≤200)和圆柱形截面长度Ls(10≤x4≤200),以及4个约束条件,压力容器设计问题数学模型如下: (20) 表6记录了9种算法优化压力容器设计的结果,CHMPFA获得的最优解为[Ts,Th,R,Ls]=[0.778 2,0.384 65,40.319 6,199.999 7],最优值f(X)=5 885.334 5,CHMPFA比其它8种元启发式算法的优化效果出色,有较低的设计成本,在压力容器设计问题中起到了良好的优化效果。 表6 压力容器设计问题最优方案 为提升标准PFA的收敛速度和寻优精度,提出了一种嵌入Cat映射的混合变异探路者算法(CHMPFA)。通过仿真实验与其它8种具有代表性的智能优化算法进行性能对比,验证CHMPFA多种策略的有效性,并将CHMPFA应用于压力容器问题中,其良好的优化效果和稳定性表明了CHMPFA的鲁棒性。未来考虑应用CHMPFA解决多目标优化问题或更为复杂的实际问题。2.5 时间复杂度分析
3 实验仿真与结果分析
3.1 实验设计
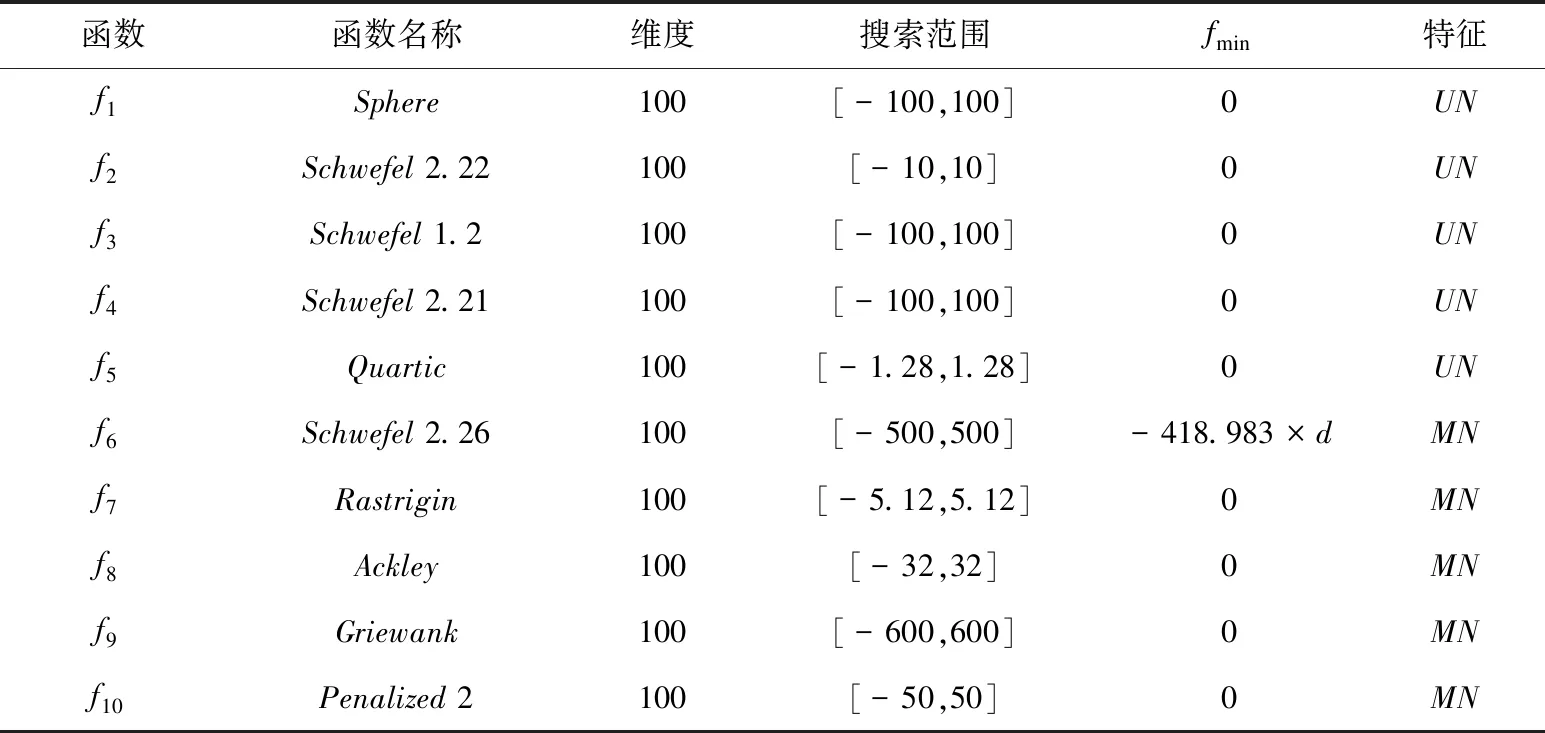

3.2 寻优性能对比分析
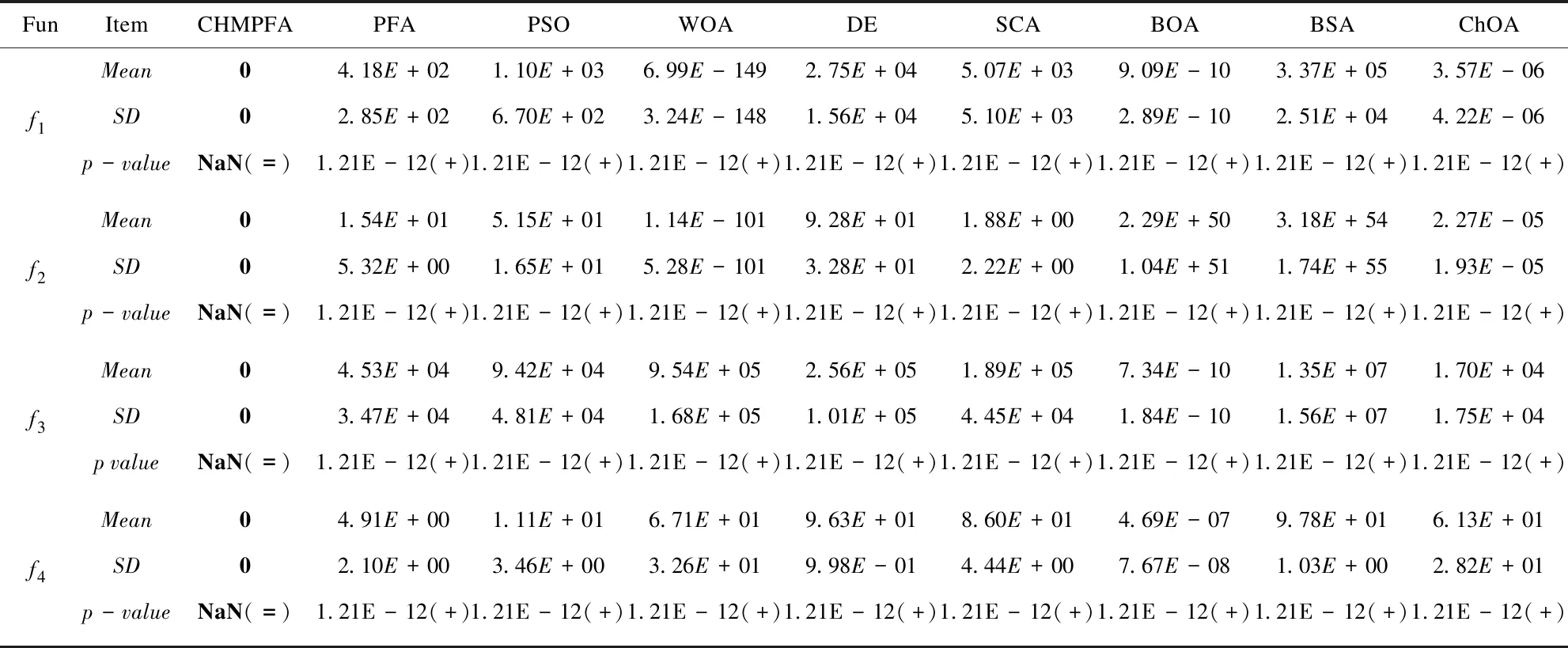
3.3 收敛曲线分析

3.4 CEC2017基准测试函数求解实验

4 压力容器设计问题
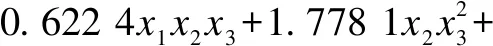
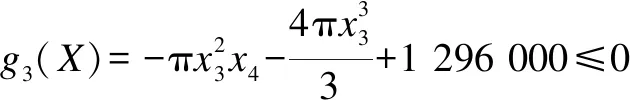
5 结束语
