深空再入飞行器烧蚀粗糙表面高超声速转捩预测

李 齐, 赵 瑞, 陈 智, 郭 斌, 王 强

(1. 北京空间飞行器总体设计部, 北京 100094; 2. 北京理工大学, 北京 100081;3. 中国航天空气动力技术研究院, 北京100074)

引 言

人类自开启航天事业以来, 探索地外天体的目标从未停止, 并且越来越深远。20世纪50～60年代, 美国与苏联分别提出了各自的月球探测计划, 并先后实现了月球采样返回和载人登月返回[1]。20世纪90年代, 美国和日本等国家又先后启动了彗尘[2]、 太阳风[3]、 小行星[4]等探测取样返回计划, 并于2004—2010年期间先后实现了样品取样返回。2014年11月, 我国首次实施月地高速再入返回获得圆满成功, 掌握了第二宇宙速度再入返回技术[5], 并以此为基础于2020年12月成功实现了月球取样返回目标[6]。2017年12月, 时任美国总统特朗普签署白宫1号太空政策指令, 重启登月计划, 目标在2025年前后重返月球, 实现新世纪载人月球探测[7]。2022年1月28日由中华人民共和国国务院新闻办公室发布的《2021中国的航天》白皮书中提出, 未来五年要“发射小行星探测器、 完成近地小行星采样和主带彗星探测”, 并“深化载人登月方案论证, 组织开展关键技术攻关”[8]。由此可见, 月球与深空地外天体探测(含载人探测)是未来世界各国空间探测与科学研究的热点项目。而开展月球与深空地外天体探测, 必然少不了样品或载人返回再入飞行器。

由于深空再入飞行器再入速度大, 为提高气动减速效率, 一般采用大钝度球冠或球锥迎风外形[9]。而大钝头迎风外形与超高速来流相互作用, 加之高温真实气体效应, 导致钝头表面热流高、 加热量大。为有效降低气动加热对主体结构、 舱体设备和航天员安全性带来的影响, 防热结构须采用碳基烧蚀型材料。而碳基防热材料密度低、 易烧蚀, 在高焓高热流长时间气动加热下会造成防热结构表面粗糙度急剧增加, 形成分布式粗糙元表面。扁平的迎风前体与粗糙元结构结合, 极易造成深空再入飞行器迎风面在高超声速下出现流动失稳, 导致流动转捩甚至演化为湍流, 使表面热流分布发生巨大变化, 给飞行器安全带来极大挑战。其中的典型案例包括: Genesis返回舱防热罩对接孔凹坑后缘流动转捩造成的局部过热问题[10], 以及NASA对Artemis 1号飞行试验返回后的猎户座飞船开展技术分析时发现了“大底隔热板烧蚀量大于地面设计预估值”的问题[11]。为适应深空探测复杂系统与运载能力之间的匹配[12], 再入飞行器质量约束是系统设计必须满足的关键条件, 因此防热结构设计必须做到节约而高效。由此可见, 深空再入飞行器高超声速边界层失稳机制分析和转捩位置的准确预测是影响深空再入返回飞行安全性的关键难题。

高超声速边界层转捩研究一般主要面向尖前缘的高超声速飞行器外形, 国内外学者曾在失稳特征、 转捩机理、 感受性特征以及转捩预测方法等方面取得了一些研究成果[13]。对于再入飞行器大钝头前体造成的流动转捩及其热影响问题, 早期在Apollo[14]、 Galileo和Pioneer Venus等[15]进/再入器上都发现过转捩现象, 但由于条件限制等问题, 未见深入的分析研究。Edquist等[16]首次针对火星探测器MSL(Mars smart lander)的大钝头前体外形利用地面试验确定的动量Reynolds数半经验工程方法来预测流动转捩的发生位置, 但后来与飞行试验结果对比发现有相当大的出入[17]。此外, Horvath等[18]分别利用细长锥外形、 MSL和Genesis号外形[19], 通过开展高超声速风洞试验和PSE方法的稳定性分析, 研究了对应外形下不同形式的表面粗糙度结构对钝头再入器迎风锥表面转捩模式的作用, 并综合了磷光测热结果和数值模拟结果, 确定了转捩发展造成的气动热分布变化, 提出了基于工程拟合的粗糙度转捩预测模型。

综上所述, 目前大部分对于高超声速边界层转捩的计算研究都是单独针对宏观外形或粗糙表面微观外形而开展的, 且大部分是基于地面试验数据进行转捩准则的建立与修正。对于大钝头宏观外形与分布式粗糙表面微观外形结合下的高超声速转捩问题, 转捩机制与基于转捩模式的数值预测研究较为少见。本文拟用适用于深空再入返回的大钝头迎风大底外形与沙粒式分布粗糙烧蚀表面为研究对象, 分别基于高超声速与粗糙元修正的γ-Reθ转捩模式和k-ω-γ转捩模式, 开展高超声速边界层转捩位置预测、 机制分析和参数影响规律研究。

1 数值方法

1.1 控制方程与数值格式

考虑量热完全气体, 对三维非定常可压缩Navier-Stokes(N-S)方程进行Favre平均, 得到可压缩湍流的Reynolds平均N-S方程

式中,ui,p,E,h分别为速度分量、 压力、 总能、 焓。且

其中,T,μl,κl分别为温度、 分子黏性系数、 分子热交换系数。

考虑高温真实气体效应的流动控制方程为积分形式的多组分化学非平衡N-S方程[20], 忽略辐射以及彻体力的影响, 方程形式如下

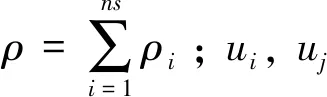
本文针对高温真实气体效应, 采用了基于5组分的Dunn-Kang模型[21], 考虑了完全催化壁模型[22], 采用了AUSM+up格式[23]进行数值解算。

1.2 湍流模型

采用基于涡黏性假设的两方程剪切应力输运(shear-stress-transport, SST) 湍流模型, 在边界层的黏性底层和对数律层采用k-ω模型, 在边界层的亏损律层采用k-ω模型和k-ε模型的混合, 在自由剪切层中采用k-ε模型[24]。控制方程为

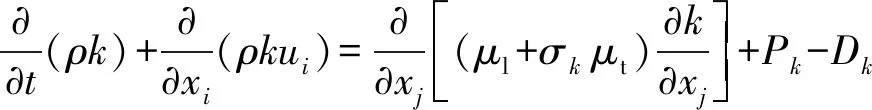
其中

湍流运动黏性系数μt和动力黏性系数νt为

模型常数由两部分混合求得

φ=F1φ1+(1-F1)φ2

混合函数F1及其他函数定义如下

1.3 转捩模式

1.3.1γ-Reθ转捩模式

γ-Reθ转捩模式通过联立求解间歇因子与转捩动量厚度Reynolds数的输运方程, 根据局部涡量Reynolds数和临界动量厚度Reynolds数的比值判断转捩[25]。γ-Reθ关联模型的间歇因子γ与动量厚度Reynolds数Reθ的方程分别为

Pγ=Flengthca1ρS(γFonset)0.5(1-ce1γ)
Dγ=ca2ρΩγFturb(ce2γ-1)

为适应高超声速转捩流动

Flength=20,ce2=20

为考虑表面粗糙度对边界层转捩的影响, 对转捩模型中的经验关系式进行修正[26]。引入等效沙粒高度ks和当地边界层位移厚度对转捩动量厚度Reynolds数进行修正, 建立粗糙表面条件下转捩动量厚度Reynolds数Reθt_rough, 表达式如下

其中

fTu=max[0.9, 1.61-1.15·e-Tu]

fΛ用于描述粗糙度的形状、 排列规律等几何构型, 本文取1。

此外, 为考虑表面粗糙度对流动转捩后湍流边界层的影响, 对SST湍流模型中比耗散率ω进行表面粗糙度修正[27], 具体形式如下

其中,SR定义如下

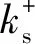
1.3.2k-ω-γ转捩模式

k-ω-γ转捩模式以SST湍流模型为基础, 由关于湍动能k、 比耗散率ω以及间歇因子γ的3个输运方程构成, 可以在有效黏性系数中考虑非湍流脉动影响, 并借鉴Langtry等[25]和Langel等[26]构造的转捩模型基于当地变量的优点, 构造了间歇因子γ输运方程耦合层、 湍流计算。其总体框架为

式中,Pγ和Dγ分别为γ输运方程的生成项和耗散项, 基于量纲分析构造, 具体表达式为

式中,Fonset为转捩起始位置函数,d为物面距离,Eu为当地流体相对壁面的平均流动动能,ν为分子运动黏性系数。有

其中,ζeff为有效长度尺度防热结构烧蚀导致的表面粗糙, 可简化为等效沙粒分布式粗糙度, 在k-ω-γ转捩模式中引入粗糙度放大因子Ar输运方程来描述壁面粗糙度对边界层转捩的影响机理和作用效果[28], 具体构造如下

Ar的壁面边界条件以Sigmoid函数给定

下式中,k+是无量纲的等效沙粒粗糙度高度, 由壁面摩擦速度uτ和等效粗糙度高度ks共同决定

1.4 方法验证

为验证本文转捩模式能否正确预测壁面粗糙度对边界层转捩的影响, 采用美国NASA兰利实验室[29]在20 in(1 in=25.4 mm),Ma=6风洞中采用的带有分布式沙粒粗糙度的半球头模型进行验证, 如图1所示, 半球模型的直径为152.4 mm。

(a) Oblique view (b) Side view

(c) Front view (b) Close-up view图1 NASA半球头模型Fig. 1 NASA hemisphere model photographs

来流条件为: Mach数6.04, 攻角0°, 壁面温度300 K, 单位Reynolds数2.18×107/m。选取80-mesh粗糙元结构来考察粗糙诱导转捩模式的预测精度, 该粗糙元均方根粗糙高度RRMS=0.03 mm。采用文献中90%粗糙度包络曲线, 并根据Dassler等[30]的经验公式, 有ks=4.33RRMS, 可得等效粗糙高度ks为0.13 mm。

图2给出了分别采用两种转捩模式考虑与不考虑粗糙度放大因子计算得到的传热系数h/href分布与地面测试结果的对比。其中, 后缀为orig表示不考虑粗糙放大因子的转捩模式计算结果, 后缀为rough表示考虑粗糙放大因子的转捩模式计算结果, exp为地面测试结果。由图可知, 在给定来流条件下, 不考虑粗糙元诱导时半球头表面流动不发生转捩, 热流由头部向肩部逐渐减小。而考虑粗糙元诱导后, 两种转捩模式计算结果均显示s/R=0.2～0.3位置边界层流动由层流转捩为湍流, 热流显著增大。由于h/href是判别流动转捩的重要宏观物理量, 由图中对比可见, 本文采用的两种粗糙元诱导转捩模式数值结果与实验测得的转捩起始位置和转捩后最高热流吻合良好。其中,k-ω-γ模式对应转捩位置与实验值吻合度更高, 而γ-Reθ模式对应转捩后热流与实验值更为接近, 这与γ-Reθ模式的转捩区模型参数由地面实验修正而来有关。

图2 不同转捩模式下半球头80-mesh粗糙模型热流密度计算值与实验值对比Fig. 2 Comparison of calculated heat flux by different transition modes and experimental heat flux of 80-mesh rough model

2 几何模型与计算状态

如图3所示, 本次研究选取的几何模型为球锥大钝头迎风大底外形, 球头半径370 mm, 迎风半锥角63°。采用分区多块对接结构网格, 不考虑侧滑角影响, 计算网格为半模, 总网格量1×106, 沿法向进行网格加密, 首层网格高度为0.03 mm, 以保证y+≤1。

(a) Symmetry plane (b) Object plane 图3 几何模型与网格结构示意Fig. 3 Geometric model and grid structure

本文计算状态如表1所示, 取典型深空再入飞行器高超声速状态, 高度/Mach数组合关系分别为52 km/Ma25, 49.3 km/Ma20, 45 km/Ma13, 42 km/Ma10, 根据气动加热状态分别设定壁面温度为3 400, 3 000, 2 500, 2 100 K, 考虑了1.5, 3 mm两种等效粗糙度高度。此外, 由于返回舱采用自旋弹道式再入飞行, 从宏观时间来看表面相同轴向位置的气动加热相等, 另外考虑大钝头迎风面热流均匀化与三维烧蚀传热的拉平效应等, 本文设置整个迎风大底表面采用相同的等效粗糙高度。

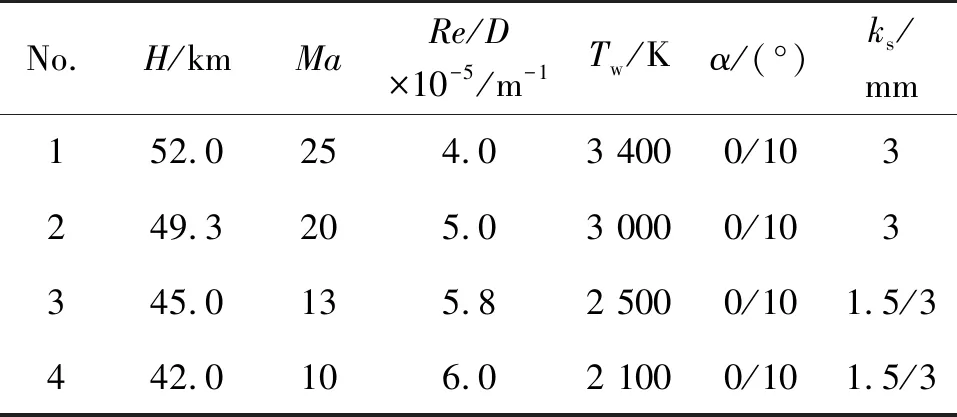
表1 再入飞行器来流条件与壁面条件

3 计算结果分析

3.1 粗糙高度对转捩模拟影响分析

采用k-ω-γ转捩模式对1.5, 3 mm等效粗糙高度的几何模型迎风大底表面间歇因子γ进行模拟分析, 图4和图5分别显示了0°攻角下状态2和状态3对应等效粗糙高度ks=1.5, 3 mm大底表面间歇因子γ的分布。k-ω-γ模式计算将间歇因子γ开始显著增长的位置定义为转捩起始位置, 将γ在(0.1～1)的范围定义为转捩区,γ>1为湍流区。由两图对比可见, 同样的来流状态下, 随着等效粗糙高度的增加, 壁面间歇因子增长起始点逐渐由肩部向中心推进。当等效粗糙高度ks=1.5 mm时, 两个状态的大底表面流动均为层流; 当粗糙高度增长为3 mm时, 两状态的大底表面在球锥面交界处开始发生转捩, 锥面大面积流动已发展为湍流。粗糙元高度通过增加当地边界层厚度而提高了当地Reynolds数, 从而促使大底表面转捩提前发生。

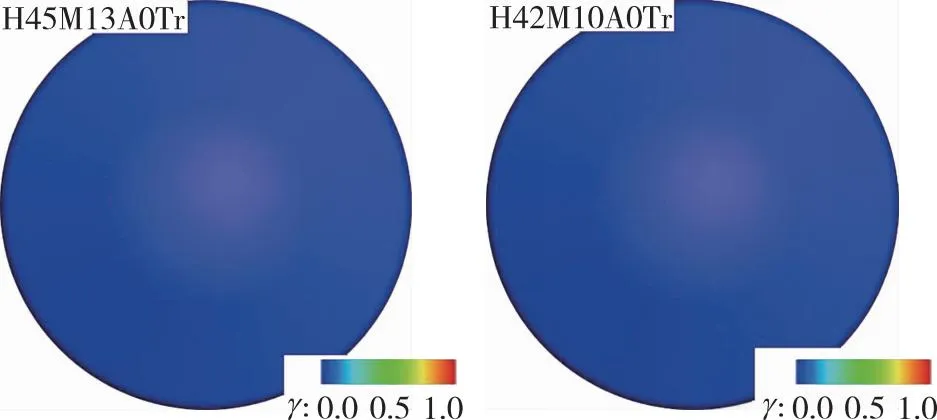
图4 壁面间歇因子分布云图(ks=1.5 mm, α=0°)Fig. 4 γ distribution on the wall(ks=1.5 mm, α=0°)

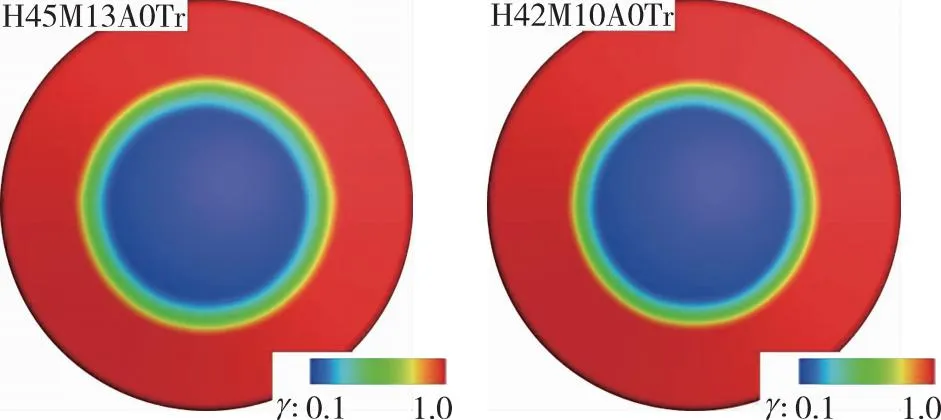
图5 壁面间歇因子分布云图(ks=3 mm, α=0°)Fig. 5 γ distribution on the wall(ks=3 mm, α=0°)

3.2 来流Reynolds数对转捩模拟影响分析

采用k-ω-γ转捩模式对不同来流Reynolds数条件下3 mm等效粗糙高度的几何模型迎风大底表面间歇因子γ进行模拟分析, 图6显示了0°攻角状态的间歇因子γ分布云图。整体来看, 在粗糙高度3 mm表面形貌下, 当前计算的所有状态下大底表面均存在转捩与湍流区。随着飞行高度的减小, 来流单位Reynolds数逐渐增大, 转捩起始位置由肩部逐渐向头部中心即上游移动; 转捩区宽度随着来流Reynolds数的增加而逐渐收缩, 而湍流区则逐渐增大。

与粗糙高度影响不同的是, 来流Reynolds数不是通过增加当地边界层厚度而是通过直接提高当地Reynolds数水平诱导转捩提前。与粗糙高度相比, 来流Reynolds数对转捩起始位置与转捩区的影响线性度更强。

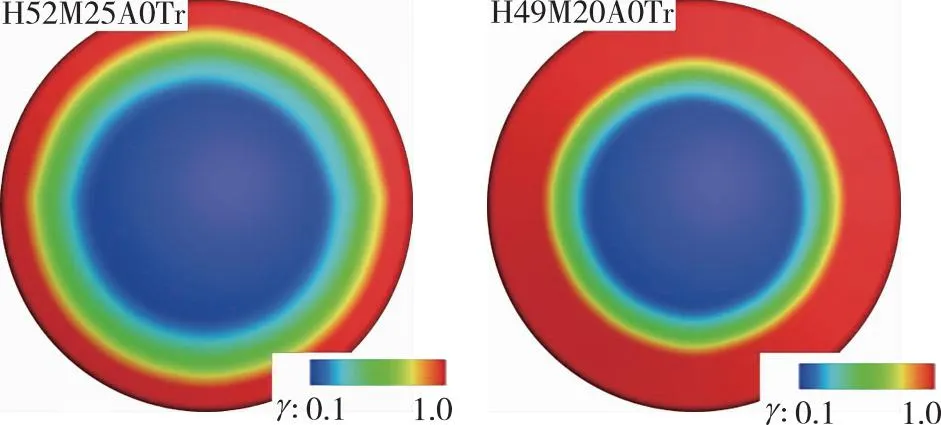
(a) Re/D=4.0×105/m (b) Re/D=5.0×105/m

(c) Re/D=5.8×105/m (d) Re/D=6.0×105/m图6 不同来流Reynolds数下壁面间歇因子分布云图(ks=3 mm, α=0°)Fig. 6 γ distribution on the wall at different inflow Reynolds numbers(ks=3 mm, α=0°)

3.3 攻角对转捩影响分析

图7为状态4、 10°攻角、 等效粗糙高度ks=3 mm条件下返回舱壁面间歇因子分布云图。与图6(d)对比可知, 由于攻角的存在, 转捩起始位置提前, 驻点向迎风面移动, 转捩区不再关于y=0对称, 而是大部分位于迎风面。图8为状态4、 10°攻角、 等效粗糙高度ks=3 mm条件下层流与转捩模式计算所得大底子午线壁面热流分布曲线的对比。与图7相对应, 由于攻角的存在, 子午线壁面热流分布曲线结果没有关于y=0对称, 转捩模式背风面热流值大于迎风面, 转捩后背风肩部热流甚至与迎风肩部相当, 可达当地层流热流的2倍以上。由上述结果分析可知, 由于攻角的存在, 大底背风面转捩位置提前, 湍流区扩大, 热流增长效应显著增加。

在一般认识下, 当有攻角存在时, 大底迎风面密度应大于背风面密度(图9(a)), 因而迎风面动量厚度Reynolds数应大于背风面。但据上述计算结果可知, 大底背风面反而转捩提前。从大底迎背风面动量厚度对比(图9(b))可知, 虽然大底迎风面的边界层外缘密度是背风面的2～3倍, 但背风面的动量厚度为迎风面的3倍以上, 且动量厚度增加导致背风面边界层外缘速度也远大于迎风面, 由此导致背风面的动量厚度Reynolds数是迎风面的1.5倍以上(图9(c))。由此可见, 有攻角情况下, 大底背风面动量厚度大大增加, 从而导致背风面动量厚度Reynolds数增大, 因此转捩位置提前, 湍流区扩大。

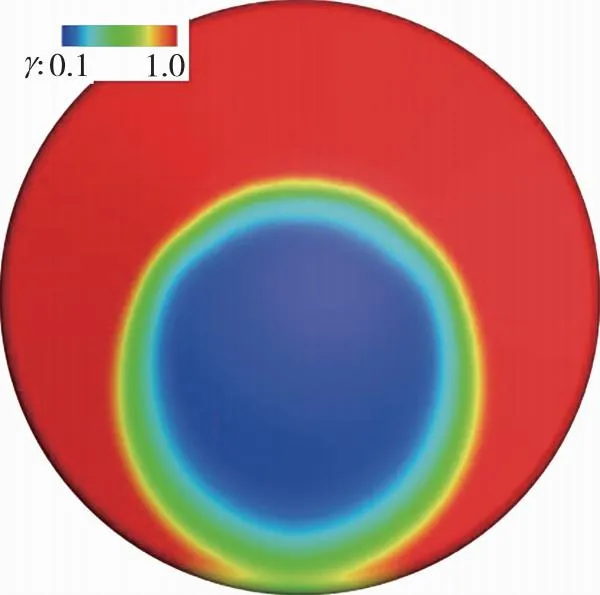
图7 壁面间歇因子分布云图(42 km/Ma10, α=10°, ks=3 mm)Fig. 7 γ distribution on the wall(42 km/Ma10, α=10°, ks=3 mm)

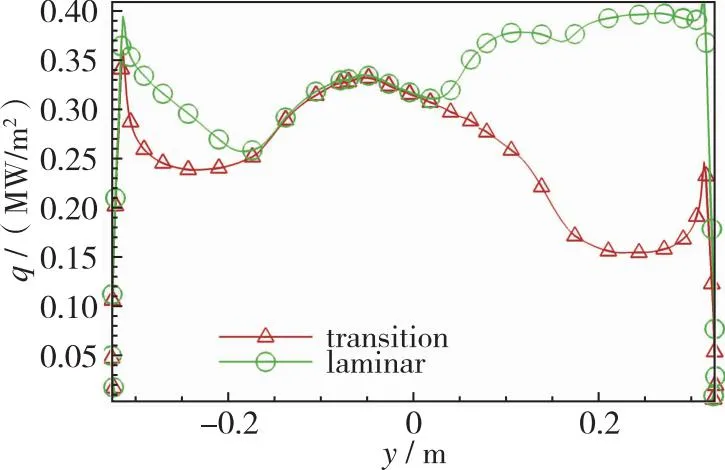
图8 大底子午线壁面热流分布曲线(42 km/Ma10, α=10°, ks=3 mm)Fig. 8 Wall heat flow distribution along the meridian of heat shield(42 km/Ma10, α=10°, ks=3 mm)

(a) Density distribution

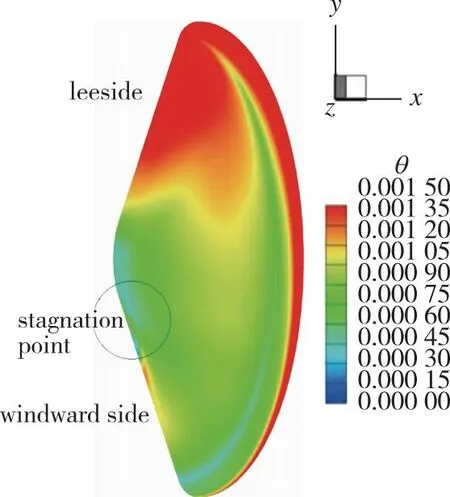
(b) Momentum thickness distribution

(c) Momentum thickness Reynolds number distribution图9 有攻角下大底表面特征参数分布(42 km/Ma10, α=10°)Fig. 9 Feature parameter distribution of the heat shield with attack angle(42 km/Ma10, α=10°)

3.4 化学非平衡对转捩模拟影响分析

采用γ-Reθ转捩模式, 分别基于完全气体和化学非平衡两种气体模型的基本流, 对不同高度状态下3 mm等效粗糙高度的几何模型迎风大底表面的热流密度分布进行模拟计算, 图10给出了状态1和状态2不同气体模型对应的层流/转捩模式下粗糙大底表面热流密度分布曲线的对比。由图可见, 在所计算状态下, 完全气体基本流计算所得热流在球锥交界位置即开始高于层流热流, 且随着高度的降低和来流Reynolds数的增加, 完全气体模型在转捩与湍流区的热流可达1.4倍以上的当地层流热流; 而化学非平衡基本流所得热流在不同高度下与层流热流则没有明显变化。由此可见, 化学非平衡基本流可有效抑制高超声速边界层转捩的发展及对热流的影响。

(a) 52 km/Ma25 perfect gas

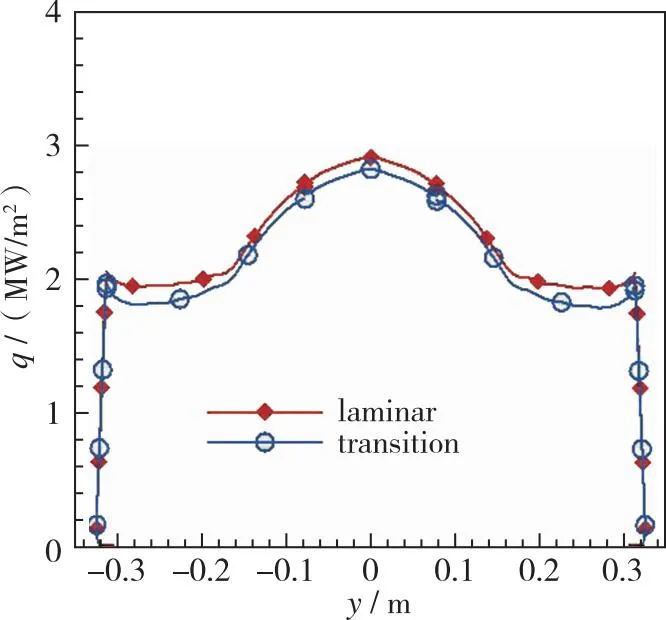
(b) 52 km/Ma25 chemical non-equilibrium

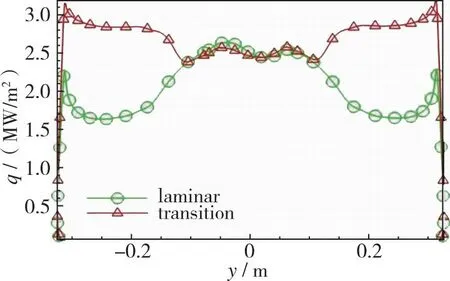
(c) 49.3 km/Ma20 perfect gas

(d) 49.3 km/Ma20 chemical non-equilibrium图10 不同气体模型下大底子午线壁面热流分布曲线(α=0°, ks=3 mm)Fig. 10 Wall heat flow distribution along the meridian of heat shield with different gas models (α=10°, ks=3 mm)

4 结论

本文以典型深空再入飞行器迎风大底外形为研究对象, 以分布式粗糙元结构为表面特征, 采用基于粗糙放大因子修正的γ-Reθ与k-ω-γ转捩模式, 对深空再入高超声速典型状态开展了边界层转捩预测模拟研究, 分析了粗糙高度、 来流Reynolds数、 攻角以及化学非平衡基本流对深空再入飞行器高超声速边界层转捩位置与转捩热效应的影响规律。主要结论如下:

1) 对于本次研究的小尺寸大钝头迎风前体外形, 分布式粗糙元与来流Reynolds数的增加都会通过增大当地Reynolds数从而诱导转捩, 使转捩起始位置逐渐向上游发展。其中, 粗糙元诱导转捩效应更为明显, 非线性度更强。

2) 攻角可使得背风面动量厚度Reynolds数大大增加, 从而导致转捩位置提前, 湍流区扩大, 背风面热流显著增长。

3) 化学非平衡基本流可有效抑制高超声速边界层转捩的发展。

后续, 对于深空再入飞行器烧蚀粗糙表面高超声速边界层转捩预测与影响分析的研究, 可围绕粗糙度对流动稳定性的影响机制分析、 建立基于粗糙元感受的流动稳定性分析模型、 建立多种分布式粗糙元等效粗糙因子数学模型等方面来开展。