基于Isight的二元进气道压缩楔射流控制参数优化
2024-02-20孙冯涛史志伟张伟麟丁保政舒彦淋
孙冯涛, 史志伟, 张伟麟, 丁保政, 舒彦淋
(南京航空航天大学航空学院, 江苏南京 210016)
引 言
自高超声速飞行的概念提出以来, 以超燃冲压发动机为动力的吸气式高超声速飞行器研究日益受到关注[1]。高超声速进气道作为现代高超声速飞行器的重要组成部分, 飞行空域广、 速域大。对于固定几何的进气道, 当来流Mach数低于设计Mach数时, 进气道的喉道流通能力低, 进气道不易起动; 当来流Mach数高于设计Mach数时, 压缩激波容易直接打入进气道唇口, 使得进气道进入超额定状态, 容易引发激波干扰降低进气道性能。
为使二元进气道能够满足现代化飞行的宽速域要求, 采用变几何进气道或者加入主动流动控制, 均可在一定程度上提高进气道性能。变形控制方式主要以形状记忆合金作为载体, 根据记忆合金形状随温度变化而变化的特性改变几何体局部形状达到控制效果[2-4]; 主动控制方式包括射流激励[5-9]、 壁面抽吸[10-12]、 磁流体控制[13-15]、 合成射流[16-18]、 等离子体控制[19-21]等, 可以应对复杂流场环境, 达到高效、 准确的控制效果。对于射流激励方面, Haws等[5]在21世纪初针对射流激励控制高超声速进气道前体激波进行了研究, 通过改变射流强度探究射流对进气道前体激波的控制效果。南京航空航天大学的Tan等[8]在Haws的基础上提出一种新型射流激励方式, 通过注入少量射流迫使边界层向外偏转, 从而使得激波也向外偏转, 实现控制激波角度的目的。南京航空航天大学的靳守林[9]针对该种射流激励, 通过数值模拟和实验验证, 证明了该方法在提高二元进气道总压恢复系数方面的可行性, 并初步探究了不同射流激励参数(射流角度、 射流宽度、 以及射流位置)对总压恢复系数的影响, 但没有给出射流激励器的最优参数。变型面控制和主动流动控制均可以一定程度上提升进气道的性能, 但要使得进气道性能在非设计工况下实现最大化, 须进一步开展优化设计。国内外研究人员对此进行了诸多研究。
Damm等[22]采用离散伴随梯度法对NASA P2高超声速进气道进行了优化设计。Kline等[23-25]基于连续伴随梯度法对二维高超声速前体-进气道进行优化以获得最大推力, 理论上, 伴随梯度法可以处理多变量高超声速前体-进气道优化问题, 然而该方法容易陷入局部最优解。Shukle等[26]以最大总压恢复系数为目标函数, 以进气道出口气流均匀性为约束条件对二元进气道进行优化。Brown等[27]采用进化算法, 以压力恢复系数(pressure recovery factor, PRF)最大和PRF方差最小为目标函数, 对具有3个压缩拐角的二维超燃冲压发动机进气道进行了优化设计。国内研究者也对二元进气道的优化设计展开了相关研究。孙菲等[28]针对高超声速二元进气道提出了一种优化方法, 采用遗传算法, 以总压恢复系数和喉道Mach数为优化目标, 流量系数为约束条件进行优化。范晓樯等[29]建立了二元进气道的参数化设计方法, 为二元进气道的优化设计提供了便捷的变参数路径。Wu等[30,31]采用基于代理模型的逐次优化策略对二维高超声速前体进气道进行整体优化, 结果表明, 数据驱动优化方法与梯度优化方法一样高效, 但精度较低。
大部分优化算法可以在进气道型面优化上得到较好的应用, 但在射流激励基础上开展的进气道优化方案较少。为此, 在射流激励条件下, 保证进气道流量系数满足性能要求, 如何实现总压恢复系数最大具有重要的研究意义。本文以二元两级压缩进气道模型为研究对象, 进气道设计Mach数为4.0, 流动控制Mach数为6.0, 在两个压缩面上分别布置一个射流激励器, 基于Isight对射流角度和射流宽度进行参数优化, 使得进气道的总压恢复系数最大, 并对优化前后的流场进行对比分析。
1 进气道模型及数值验证
1.1 进气道模型
进气道模型为二元两级压缩进气道模型, 如图1所示, 主要由两级外压缩面和内通道两部分组成, 内通道转角和唇口内侧均采用圆弧过渡处理, 以削弱流场因结构外形改变而发生角度偏转产生的斜激波[9]。进气道主要设计参数如表1所示。
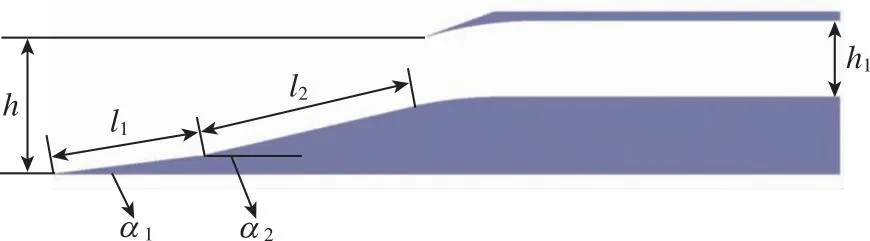
图1 进气道模型Fig. 1 Inlet model

表1 进气道主要设计参数
1.2 数值验证
本文的数值模拟方法采用隐式耦合求解二维Reynolds平均N-S方程, 湍流模型选取SSTk-ω模型, 为提升数值计算中对近壁面边界层流场的计算精度, 对近壁面的网格均进行了加密, 以确保y+小于1。采用Roe-FDS计算格式和2阶迎风离散, 计算工况均为0°攻角0°侧滑角。模型网格选用结构化网格, 唇口附近局部网格如图2所示, 来流条件为压力远场, 来流Mach数(Ma∞)为6, 来流静压1 260 Pa, 静温73.2 K, 进气道内通道出口和远场出口均为压力出口。

图2 唇口附近局部网格Fig. 2 Local grid near the lip
对Ma∞=6的工况进行了数值计算, 数值计算方法和边界条件与前文所述一致。为验证所用数值方法的准确性, 选用1.9×105, 3.3×105, 5.0×105网格量模型作为3种不同疏密程度的网格, 参考文献[9]的实验结果进行算例验证, 图3为数值计算和实验的激波分布, 图4为实验和数值计算下内通道下壁面静压系数分布, 可见中等网格和密网格捕捉到的激波较精细, 并且内通道中的分离区清晰可见, 而稀疏网格捕捉的激波粗糙。对比数值计算和实验的内通道下壁面压力系数, 中等网格和密网格的计算结果和实验结果符合良好, 能够保证所用数值方法的可靠性。为在保证计算精度的同时节约计算资源, 本研究选取中等网格量进行后续数值计算。
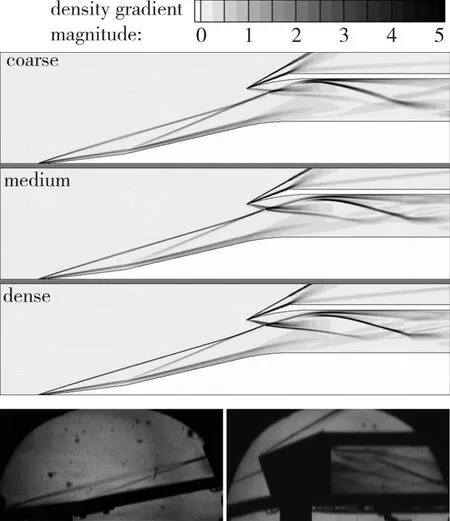
图3 数值仿真密度梯度图和实验纹影图Fig. 3 Contour of density gradient magnitude and experimental schlieren
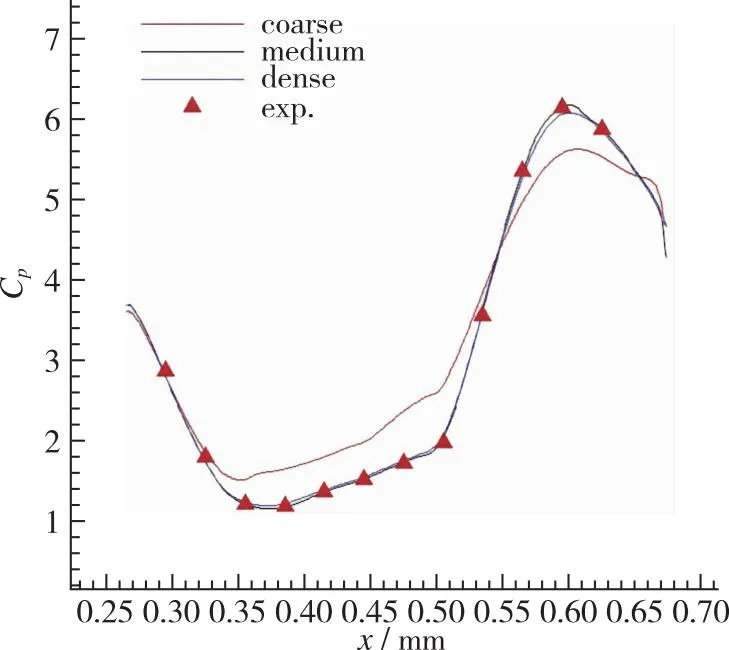
图4 数值仿真和实验内通道下壁面压力系数分布Fig. 4 Comparison of lower-wall pressure coefficient between simulation and experiment
2 射流角度参数优化
2.1 优化变量及目标函数
在两级压缩面上分别布置一个射流激励器, 射流激励器边界条件为压力入口, 射流激励器参数如图5所示。射流角度定义为射流前缘壁面与压缩面壁面之间的夹角θ, 射流宽度W为射流壁面之间的距离, 射流位置以射流前缘壁面到压缩面前缘拐点的距离D定义,Pr为射流压比, 定义为射流静压与来流静压之比。射流缝截面形状始终被约束为平行四边形。选取射流角度θ和射流压比Pr作为优化变量, 射流位置D=5 mm, 射流宽度W=10 mm, 以出口总压恢复系数σ最大为目标函数进行优化, 同时以流量系数φ为约束条件(0.9<φ<1.05), 且在优化结果的后处理过程中需剔除不满足约束条件的样本点, 保证在满足流量系数的前提下最大化进气道的总压恢复系数。

图5 射流激励器参数Fig. 5 Parameters of jet exciter
射流角度优化变量的初值和取值范围在表2中列出。θ1和Pr1分别为一级压缩面上射流激励器的射流角度和射流压比,θ2和Pr2分别为二级压缩面上射流激励器的射流角度和射流压比。由于要在最大化总压恢复系数的同时减小射流流量损耗, 还要兼顾寻优范围不能过小, 所以将射流压比限制在2~6。为方便后续表述, 将一级压缩面上的射流缝称为一级射流缝, 二级压缩面上的射流缝称为二级射流缝。
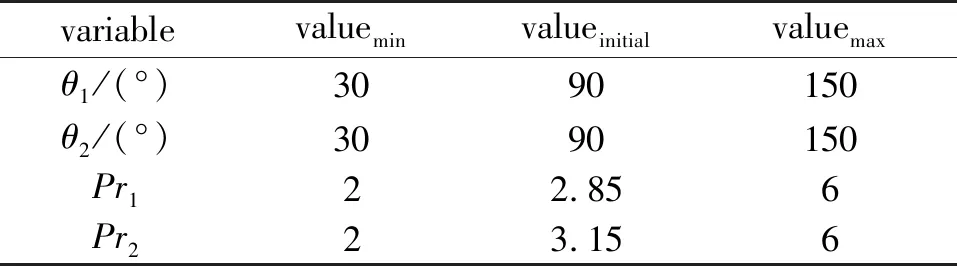
表2 射流角度优化变量取值范围
2.2 优化方法
对于射流角度优化来说, 优化变量为射流角度和射流压比, 总共为4个待优化变量。遗传算法计算变量较多的优化问题时效率偏低, 计算代价大; 梯度算法利用梯度信息计算局部最优解, 处理多变量优化问题效率高; 直接搜索法不需要计算函数梯度, 而是通过相应的搜索步长来直接搜索最优解。由于该优化问题中的优化变量较多, 本文选取Hooke-Jeeves优化方法, 该算法不需要连续的目标函数, 能很好地处理多变量优化问题, 同时能迅速收敛到局部最优解[32]。对于Hooke-Jeeves优化方法而言, 最终寻得的最优解很大程度上受到优化变量初值的影响, 为解决局部最优解问题, 须结合进气道SOC(shock-on-cowl)原则, 即进气道前体激波汇聚在唇口时, 进气道性能达到最优, 因此选取激波汇聚在唇口附近的参数值作为优化初值, 此时寻得的最优解即可视为全局最优解。
2.3 优化流程
利用Isight软件搭建整体优化流程, 图6是Isight优化求解过程。以优化射流角度和射流宽度为例说明整个优化流程的运行。首先在Value_input中输入射流参数, 设置射流角度为90°, 射流宽度为10 mm, 将射流参数传递给Catia模块, 按照输入参数值改变射流角度和射流宽度, 之后将改变射流参数后的进气道模型传递给Pointwise模块, 按照预先在软件中录制好的脚本文件进行网格划分并输出cas文件, 该射流参数下的射流激励器模型及网格划分如图7(a)所示; Fluent模块除了读取Pointwise模块输出的cas文件外, 还须嵌入编写的Jou脚本文件进行边界条件设置和求解设置, 数值计算完成后通过Calculator模块计算进气道性能参数, 计算收敛结果如图7(b)所示, 最后将进气道性能参数输出至优化模块(Optimization1), 根据目标函数对性能参数进行评估并优化射流参数, 同时将其传递给Value_input模块, 以上过程不断循环迭代直至目标函数收敛。

图6 Isight优化流程Fig. 6 Optimization process of Isight

(a) Mesh generation

(b) Simulation results
Hooke-Jeeves优化方法包括两个关键参数: 相对步长和步长缩减因子。相对步长是指算法在最初寻优时和设计变量的初始值共同决定扰动范围, 该参数在本问题取0.5。步长缩减因子的取值范围在0~1之间, 该值越大, 收敛的可能性就越大, 但是评估函数的时间相应增加。该值越小, 函数的评估和程序运行的时间越少, 但不收敛的可能性会增加[32]。本问题折中取0.5。对于射流角度的优化, 优化迭代100步后目标函数收敛, 各优化变量收敛过程如图8所示。

(a) Objective function(total pressure recovery coefficient)
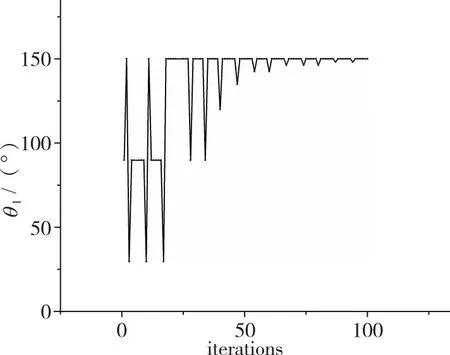
(b) First jet angle

(c) Second jet angle图8 目标函数及各优化变量收敛过程Fig. 8 Convergence process of objective function and optimization variables
2.4 优化结果
图8给出了优化过程中总压恢复系数和各优化变量的收敛过程。由图8(a)可知, 总压恢复系数收敛在0.49附近, 最大值为0.496, 相对于不加射流激励的本体提升了18%, 此时各优化变量的值如表3所示, 一级压缩面上的射流角度达到了约束最大值150°, 二级压缩面上的射流角度减小, 两个射流缝的射流压比相对于初值均有所增加。

表3 射流角度和压比最优值
图9为优化过程中优化点集的分布状况, 空间分布的红点为优化过程中样本的总压恢复系数值的分布, 平面分布的蓝点和黑点分别为总压恢复系数σ在yz和xz面上的投影, 结合图8、 图9, 优化迭代次数达到60左右时, 目标函数已经在σmax附近收敛, 所以优化点集大多集中在最优值附近, 寻优过程中的状态点较少。从图9优化点集分布可以看到, 在两个压缩面上, 随着射流压比Pr的增大, 总压恢复系数先增后减, 这是由于在同一射流参数条件下, 随着射流压比逐渐增大, 前体激波交汇点从唇口下方逐渐上移, 在唇口附近总压恢复系数达到最大, 随后激波交汇点继续上移远离唇口, 总压恢复系数逐渐减小。

(a) Jet angle
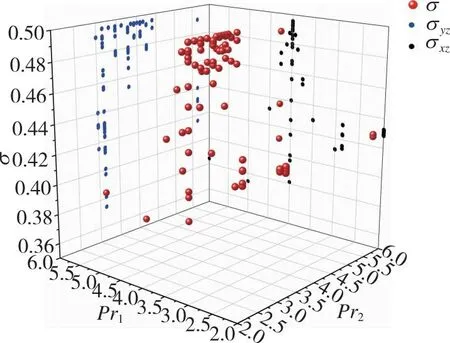
(b) Jet pressure ratio图9 优化过程中点集分布Fig. 9 Distribution of point sets during the process of optimization
总压恢复系数σ随射流角度和射流压比变化拟合云图如图10所示。随着射流角度θ1的增大, 总压恢复系数基本呈现递增的趋势, 在θ1=150°附近取得最大值; 随着θ2的增加, 总压恢复系数并没有较大变化, 表明二级压缩面上的射流角度并非影响总压恢复系数的主要因素; 同时从图10(b)(c)中可得, 随着射流角度增大, 相应实现最大总压恢复系数的射流压比并没有显著增加, 低射流压比(Pr1=2.5,Pr2=3.15)条件下即可使得大部分射流角度下的总压恢复系数达到最大值, 只有在θ1=150°附近时射流压比最大为4。
表4列出了优化前后进气道各性能的相对变化量。优化射流角度后流量系数大于1, 这是由射流注入的额外流量导致的, 此时进气道不仅满足流量系数的要求, 出口Mach数也降低了0.25%。从射流压比来看, 虽然射流压比相较于优化初值略有提高, 增加了射流流量, 但这能够使得总压恢复系数提高18%。

(a) Total pressure recovery coefficient and jet angle
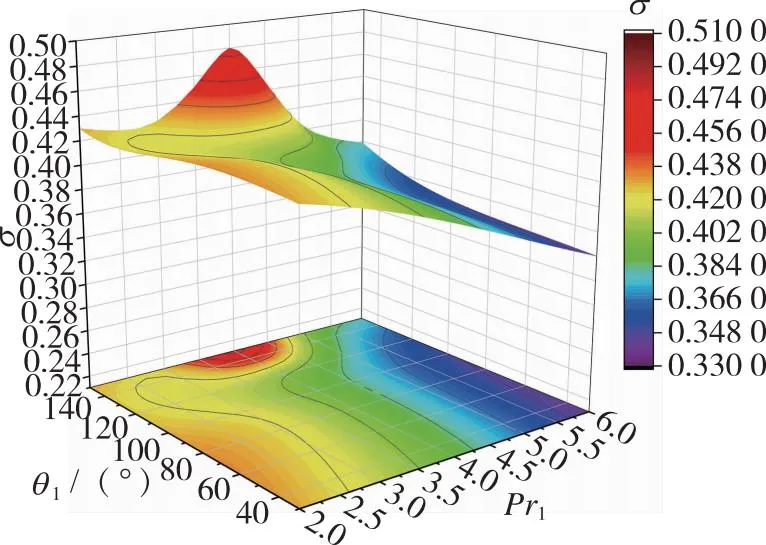
(b) Jet angle and pressure ratio of first jet

(c) Jet angle and pressure ratio of second jet图10 总压恢复系数和射流角度及射流压比拟合云图Fig. 10 Fitting contour of total pressure recovery coefficient with jet angle and pressure ratio

表4 优化前后进气道性能对比
提取优化角度后和优化过程中非最优样本点的进气道流场如图11所示, 所选非最优射流参数θ1=90°,θ2=150°,Pr1=4,Pr2=3.15, 总压恢复系数σ=0.4, 优化初值和最优角度参数已在前文给出。对比优化初值和非最优角度流场, 一级射流缝处射流压比增加, 导致第1道激波角度明显增大, 一定程度上造成溢流, 影响进气道的压缩性能; 二级射流缝处射流角度增大为150°, 有前向射流趋势, 射流切向动量效果增强, 受影响的边界层区域前移, 但是压比并没有变化, 使得法向动量效果减弱, 吹起的边界层厚度减小, 第2道激波角度略有减小; 而最优角度下, 两道激波均在唇口处封口, 且吹起的边界层厚度明显小于其余两种优化工况, 从而总压损失减小。

(a) Initial value of optimization
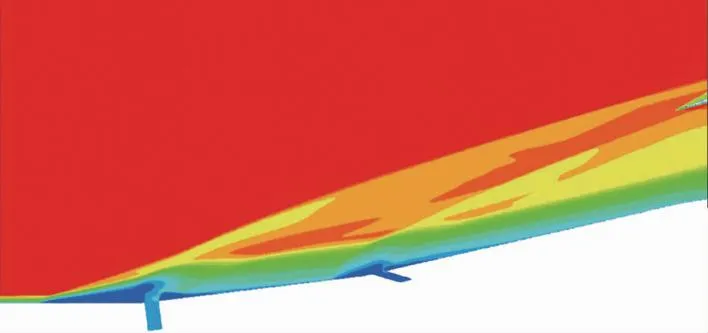
(b) Non-optimal jet angle

(c) Optimal jet angle图11 射流角度优化过程中不同样本点流场Fig. 11 Flow fields of different examples when optimizing jet angle
3 射流位置参数优化
3.1 优化流程
除射流角度外, 射流位置也是影响进气道性能的重要参数之一, 很大程度上影响激波位置以及进气道流量系数, 因此也须对其进行参数优化, 以确定最优射流位置。和射流角度优化相似, 以射流位置和射流压比为优化变量, 总压恢复系数依然作为目标函数, 优化变量的初值以及取值范围在表5中列出,D1和Pr1分别为一级射流缝的射流位置和射流压比,D2和Pr2分别为二级射流缝的射流位置和射流压比。

表5 射流位置优化变量取值范围
3.2 优化结果
在经过160次优化迭代后, 总压恢复系数达到收敛条件, 各优化变量的最优值在表6中列出, 此时目标函数和各优化变量的收敛过程如图12所示, 总压恢复系数收敛于0.5附近, 最大值为0.505, 与最优射流角度下的总压恢复系数相差不大, 同时最终的流量系数也收敛于1.0附近, 满足进气道的流量需求。对于各优化变量, 两个射流激励器的射流位置D均后移, 从二级射流缝的射流位置和射流压比来看, 虽然增大射流位置D后移可以在一定程度上增加总压恢复系数, 提高进气道性能, 但是可能会导致射流压比的增加, 造成射流流量损耗。

表6 射流位置和压比最优值

(a) Objective function(total pressure recovery coefficient)
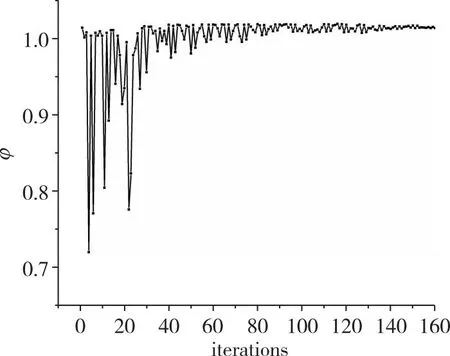
(b) Flow cofficient
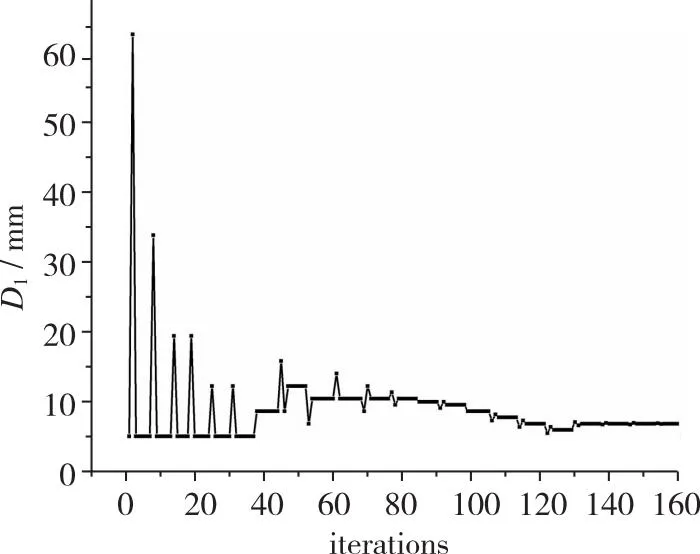
(c) First jet position D1
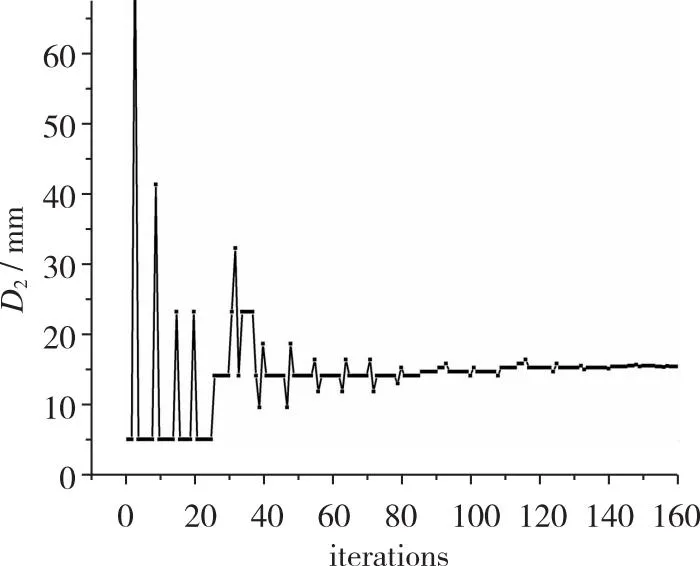
(d) Second jet position D2图12 射流位置优化时各优化变量收敛过程Fig. 12 Convergence process of optimization variables when optimizing jet position
总压恢复系数随射流位置和射流压比变化的拟合云图如图13所示, 对于一级射流缝的位置, 随着射流位置后移, 使得总压恢复系数达到最大的射流压比也相应增加; 二级射流缝的射流位置也有相似的规律, 但随着射流位置后移到一定位置时, 即使进一步增加射流压比, 也不会使总压恢复系数明显增加。综上, 射流位置后移要以牺牲射流流量为代价来提高总压恢复系数, 而对射流角度来说, 较低射流压比下就可以使得大部分射流角度参数下的进气道总压恢复系数最大化, 仅在最优值时的射流压比达到4, 其在不同射流角度下实现总压恢复系数最大的平均射流流量损耗较小。

(a) Position and pressure ratio of first jet
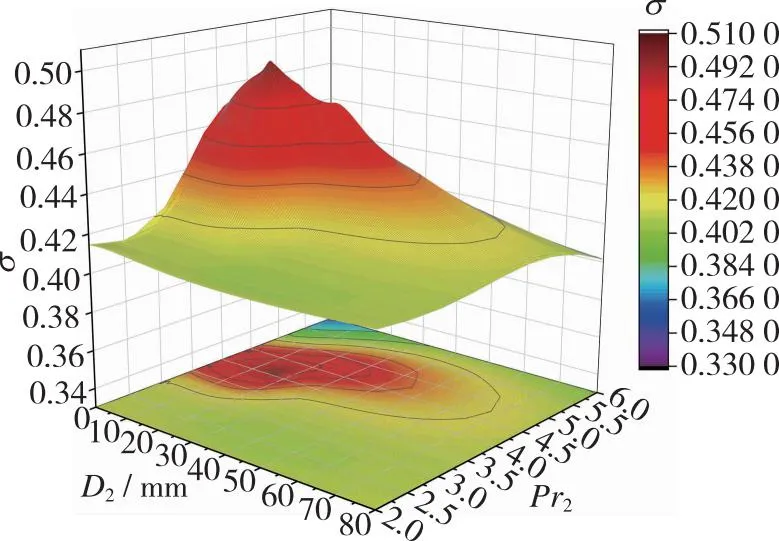
(b) Position and pressure ratio of second jet图13 总压恢复系数随射流位置和射流压比变化拟合云图Fig. 13 Fitting contour of total pressure recovery coefficient with jet position and pressure ratio
提取优化参数初值和最优射流位置的流场如图14所示, 随着射流位置后移, 射流影响区域也随之后移, 同时抬起激波到相同位置所需的压比也相应增加, 从而使得射流吹起的边界层厚度增加, 一定程度上增加了总压损失, 限制总压恢复系数的增加, 同时改变射流角度在一定程度上也会增加射流流量损耗, 如果将射流位置和射流角度同时作为优化参数, 会造成额外的射流流量损失, 结合文献[9]中对射流宽度和射流位置的研究结论: 对于射流宽度, 通过增大射流宽度能够降低对射流压比的要求; 而对于射流位置, 进气道压缩面上射流激励器的布置位置应尽可能靠近压缩面前缘, 以避免这种强射流造成额外的总压损失。考虑进气道宽速域以及低射流流量损耗的性能要求, 可以先确定一个较优的射流位置, 选用射流角度和射流宽度作为综合优化的变量, 考虑到实际应用, 射流缝应与压缩面前缘留有一定的距离, 所以射流激励器的位置选用5 mm, 即D1=D2=5 mm。

(a) Initial value of optimization


(b) Optimal jet position图14 射流位置优化过程中不同样本点流场Fig. 14 Flow fields of different examples when optimizing jet position
4 射流角度与射流宽度综合优化
4.1 优化流程
在原有射流角度的基础上增加射流宽度作为优化变量, 优化方法和优化流程与射流角度参数优化相同。优化变量取值范围如表7所示。其中,θ1,W1,Pr1分别为一级压缩面上射流激励器的射流角度、 射流宽度和射流压比,θ2,W2,Pr2分别为二级压缩面上射流激励器的射流角度、 射流宽度和射流压比。

表7 综合优化变量取值范围
4.2 优化结果
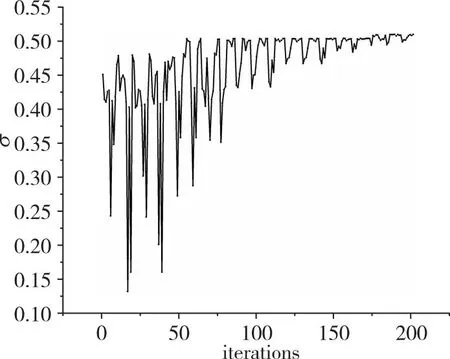
目标函数收敛过程如图15所示, 由于待优化变量数目的增加, 目标函数达到收敛所需的迭代次数也相应地增加, 在100步附近时, 已经达到目标函数最大值, 开始缩小搜索步长, 在200步时收敛于0.505附近, 最大值为0.51, 相对于不加射流激励提升了21.4%, 相对于仅优化射流角度参数提升了2.82%, 说明射流激励参数除射流角度外, 射流宽度也是影响进气道总压恢复系数的重要参数。此时优化变量的最优值如表8所示。
(a) Objective function(total pressure recovery coefficient)

(b) First jet angle
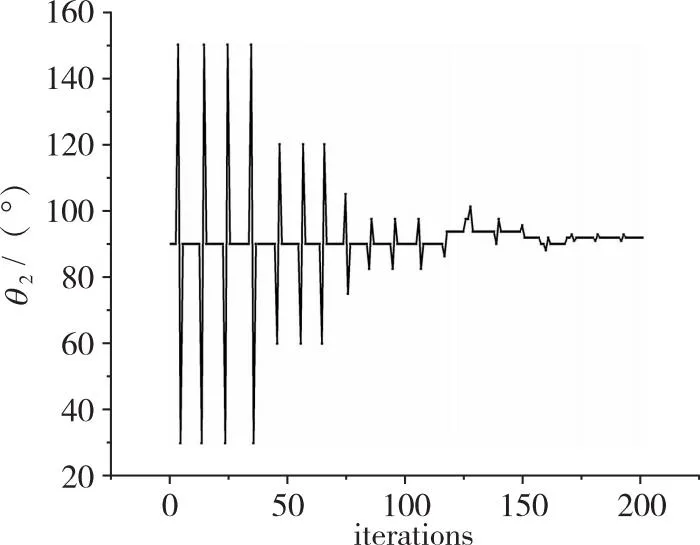
(c) Second jet angle

(d) First jet width
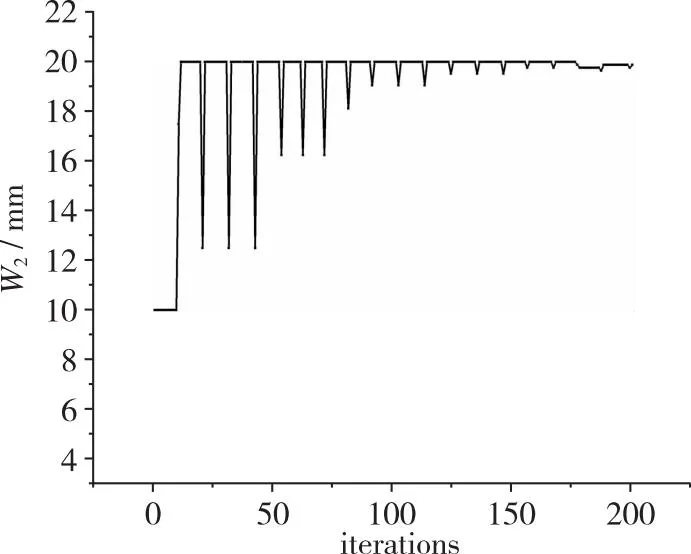
(e) Second jet width图15 综合优化各优化变量收敛过程Fig. 15 Convergence process of objective function and optimization variables of combination optimization

表8 综合优化变量最优值
表8给出了综合优化后各优化变量的最优值, 可见一级射流角度θ1的最优值不同于角度优化结果, 综合优化θ1=60°时总压恢复系数取得最大值, 可见优化过程中的射流参数作为离散量, 简单地将各射流参数组合起来不一定是全局最优解, 而二级射流角度θ2并没有太大变化, 表明θ2对总压恢复系数的影响较小; 一级射流宽度W1和二级射流宽度W2均接近约束上限, 一级射流压比Pr1和二级射流压比Pr2均没有明显改变, 可以说在没有增大射流压比的前提下, 有效地增加了总压恢复系数, 由此可见, 通过增加射流宽度可以补偿射流流量的不足, 降低对射流流量的要求。
分别拟合出总压恢复系数σ随优化变量的分布云图, 如图16所示, 可见随着θ1的增大,σ先增后减, 而θ2对σ的影响不大; 随着W1的增大,σ整体呈单调递增趋势, 而W2对总压恢复系数的影响与W1有关, 当W1在最优值附近时,σ随W2递增, 当W1较小时,σ随W2先增后减。

(a) Jet angle and total pressure recovery coefficient
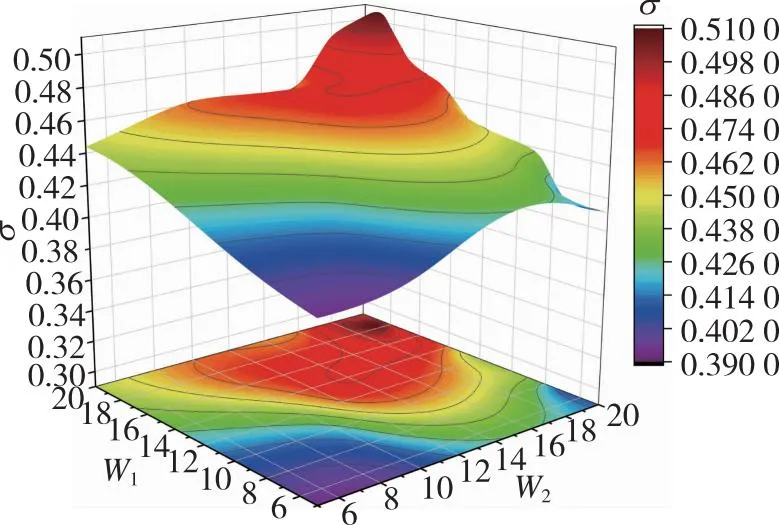
(b) Jet width and total pressure recovery coefficient
表9为综合优化后进气道性能参数, 可见加入射流宽度作为优化变量后, 总压恢复系数得到了进一步提升, 流量系数均大于1, 这是由于射流流量的注入增加了额外流量, 此外出口Mach数也没有明显变化, 整体上没有减弱进气道对来流的压缩性能。

表9 综合优化后进气道性能
提取综合优化过程中不同样本点流场, 如图17所示, 非最优参数θ1=60°,θ2=120°,W1=W2=20 mm, 3种状态的射流压比相同, 分别为Pr1=2.85,Pr2=3.15。可以看出, 通过增加射流宽度, 一定程度上抵消了射流角度变化带来的负面影响, 在不增加压比的情况下, 使得压缩面两道激波在唇口处封口, 进一步表明合理改变射流宽度能在实现激波封口的同时有效减小射流流量损失。

(a) Initial value of optimization

(b) Non-optimal parameters

(c) Optimal value of combination optimization图17 综合优化过程中不同样本点流场对比Fig. 17 Flow fields of different examples in the process of combination optimization
5 进气道流场结构分析
提取不同射流参数下进气道流场, 如图18所示, 无射流激励时, 激波直接打入唇口内侧, 形成内通道激波波系, 引发激波干扰, 降低进气道性能, 此时总压恢复系数σ=0.42; 初步加入射流激励后, 激波在射流的影响下被“抬起”, 但没有完全实现封口, 同时内通道由于激波/边界层干扰形成的分离区也相应地前移, 此时总压恢复系数σ=0.43, 相对于无射流激励有所提升; 角度优化后, 两道激波在唇口处实现封口, 进气道总压恢复系数提高至 0.496; 综合优化后的总压恢复系数达到0.51, 相对提升了2.82%,可以看出虽然在不同射流激励参数下, 均可“抬起”激波, 在唇口处实现封口, 但其封口时的总压恢复系数有所不同, 主要体现在内通道和前体压缩面的流场差异。
为方便分析内通道流场, 在内通道中提取截面如图19所示, 依次对截面编号, 其中截面1为喉道截面, 截面7为出口截面, 各截面相距50 mm。图20为两种优化结果各截面上的静压、 Mach数和总压恢复系数, 均采用质量加权平均, 可以看出内通道中沿程静压值没有太大差异, 综合优化后内通道中流速增加, 总压损失减小, 总压恢复系数均在各截面上大于角度优化, 可见前体激波同为封口状态, 内通道中流场相似, 所以主要对进气道前体流场进行对比分析。

(a) Without jet

(b) Initial value of optimization

(c) Optimal jet angle

(d) Combination optimization图18 不同射流参数下进气道流场Fig. 18 Flow fields of inlet at different jet parameters
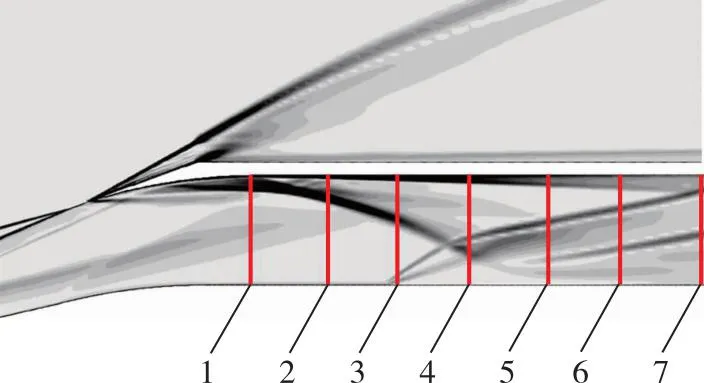
图19 内通道截面示意图Fig. 19 Sketch of inner channel cross-section
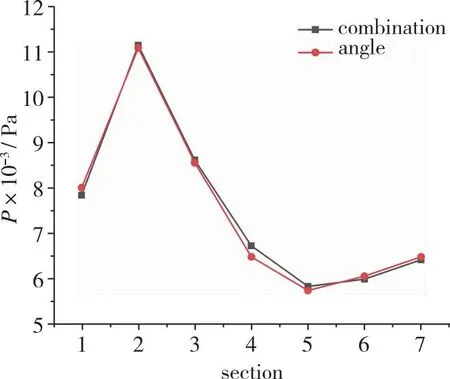
(a) Static pressure variation along sections

(b) Mach number variation along sections
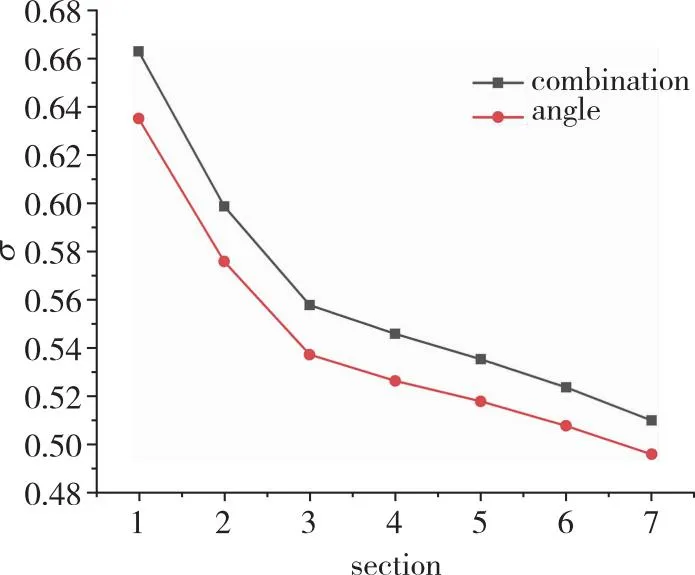
(c) Total pressure recovery cofficient variation along sections图20 内通道中各截面参数Fig. 20 Parameters of each section in the inner channel
图21为角度优化和综合优化的流场Mach数云图, 可见优化后的前体激波均在唇口处实现封口。对比射流缝结构可以看到, 对于二级射流缝, 优化前后均没有太大变化。角度优化时, 一级射流缝的θ1从优化初值的90°变为150°, 角度增大, 射流由初始的垂直于壁面方向变为前向射流; 综合优化时,θ1从优化初值的90°变为60°, 角度减小, 射流由初始的垂直于壁面方向变为后向射流。由图22中的流线图可见, 当θ1=150°时, 前向射流主要影响射流缝前缘区域, 在射流的影响下, 来流在绕过射流影响区域后迅速再附于壁面上, 形成类似于后台阶的“虚拟型面”, 在一级射流缝后缘处形成额外的分离区, 造成总压损失; 当θ1=60°时, 射流出口处的边界层均匀受到射流的影响, 来流速度变化较为平缓, 射流缝后缘附近仅在射流的直接作用下使得边界层厚度增加, 并没有形成明显的分离区, 相较于θ1=150°时降低了总压损失。
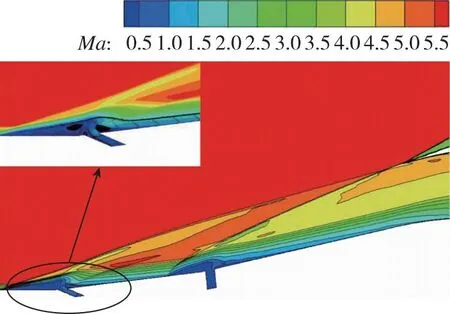
(a) Optimal jet angle
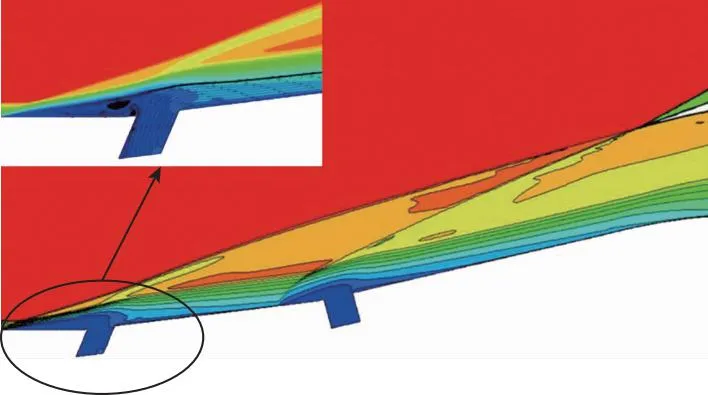
(b) Combination optimization图21 角度优化和综合优化流场Mach数云图Fig. 21 Contour of Mach number of angle optimization and combination optimization
图22为进气道前体总压恢复系数分布, 整体看来, 综合优化后流场的总压恢复系数分布更加均匀, 对于一级压缩面产生的激波, 波后总压恢复系数相差不大, 唯一不同的是θ1=150°时, 一级射流缝后缘近壁面附近总压恢复系数明显减小; 对于二级压缩面产生的激波, 综合优化的波后总压恢复系数分布明显要优于角度优化, 主要表现在唇口下方和近壁面处的总压损失少, 总压恢复系数较大。因此采用后向射流比前向更有优势, 因为前向射流会引起流动分离和再附, 造成额外的气动损失。

(a) Optimal jet angle

(b) Combination optimization图22 角度优化和综合优化流场总压恢复系数分布Fig. 22 Contour of total pressure recovery coefficient of angle optimization and combination optimization
图23, 24分别给出了不同优化结果的进气道前体密度梯度云图和压力梯度云图, 由图可见, 一级射流缝处采用前向射流会导致一级射流缝后缘处来流迅速再附, 在后缘分离区处形成诱导激波, 近壁面附近耗散更多总压, 从而减小了总压恢复系数。由于二级射流缝的射流角度相差不大, 且第2道激波均处于在唇口处封口的状态, 所以可以将二级射流缝附近流场结构的不同近似归结于射流宽度的影响, 由图24可见, 射流宽度的增加, 使得激波起点延后, 以二级射流缝前缘为参考点, 分别给出不同宽度下激波前缘点到参考点的距离, 可以看到激波宽度增加后使得激波前缘向后移动了9 mm, 减小了边界层厚度增加的区域, 同时也使得高压力梯度区域面积减小, 使得流场分布更加均匀, 从而提升总压恢复系数。


(a) Optimal jet angle

(b) Combination optimization


(a) Optimal jet angle

(b) Combination optimization
6 结论
本文通过Isight对二元两级压缩进气道前体射流角度和射流宽度进行了优化, 分析射流角度和射流宽度对进气道性能的影响, 并对优化后的进气道流场结构进行了对比分析, 得出以下结论:
1) 优化角度后的进气道前体激波在唇口处封口, 验证了Hooke-Jeeves优化方法在优化进气道前体射流激励控制优化问题上的可行性, 优化后的进气道相较于本体性能有较大的提升, 最优射流角度激励下的进气道总压恢复系数相较于本体不施加任何激励提升了18%,同时流量系数也满足进气道气动性能要求。
2) 通过优化射流位置提升总压恢复系数会导致射流流量的额外损失, 因此选择将射流角度和射流宽度作为主要优化变量进行综合优化, 优化后的总压恢复系数比仅优化射流角度高出4%, 表明射流宽度也是影响总压恢复系数的重要参数, 且射流参数在优化过程中作为离散量, 不能简单地将各个参数的最优值组合视为全局最优解。
3) 对于两级压缩进气道而言, 一级压缩面上射流角度是主要影响因素, 采用前向射流时会引起流动分离和再附, 造成额外的气动损失, 而采用后向射流时并没有形成明显的分离区, 有利于进一步提升总压恢复系数; 而二级压缩面上射流宽度为主要影响因素, 射流宽度的增加一方面减小了边界层厚度增加的区域, 同时也使得高压力梯度区域面积减小, 从而提升总压恢复系数。
