电磁助推翼段加速地面效应及稳定性分析
2024-02-20罗星东侯自豪李少伟薄靖龙翟茂春
罗星东, 侯自豪, 李少伟, 薄靖龙, 翟茂春
(中国航天科工飞航技术研究院磁电总体部, 北京 100074)
引 言
新一代空天飞行器采用组合循环动力技术, 可水平起降与重复使用, 并可自由穿梭于低空、 临近空间乃至近地轨道, 是未来争夺太空经济和军事主动权的重要途径。由于飞行过程须跨越亚、 跨、 超、 高超声速, 所以需要兼顾飞行器在宽速域、 大空域下的气动布局和组合动力效率等问题, 这对系统设计提出了极大挑战[1]。涡波效应-乘波设计、 机翼-乘波设计和变形/组合设计是目前发展宽速域飞行器的几种主要思路[2]。近年来, 电磁发射技术逐渐成熟, 为克服上述难题提供了另一种颇具潜力的解决方案[3]。利用电磁橇将飞行器在近地助推至超声速, 能够有效规避低速起飞阶段, 增加系统设计冗余度。国内外已对此开展了电磁助推发射方案验证和缩比模型试验验证[4]。不同于开域飞行, 地面为近地流动营造了独特的半开放约束空间, 通常诱发以复杂激波现象为主导的跨/超声速地面效应干扰。除空气动力学特性外, 飞行器还处于电磁弹性力-气动力-结构弹性力多物理场耦合环境中, 面临着复杂的气动弹性及稳定性问题。深入认知电磁助推加速地面效应并探索调控系统稳定性的手段是电磁发射技术开发的重要前提。
依托地效飞行器[5,6]、 航天器着陆[7,8]等研究背景, 研究人员对低亚声速地面效应已建立起较丰富的认识[9-11]。Morrow等[12]通过研究发现, 与低亚声速地面效应不同, 跨/超声速地面效应更为复杂, 以激波及其反射现象为主要特征。罗世彬等[13]综述了电磁助推发射的气动关键技术, 认为飞行器-电磁橇在加速至超声速过程中, 多体之间强烈的激波干扰会影响滑跑稳定性。
研究人员对跨/超声速地面效应开展了必要讨论。在实验研究方面, Doig等[14-16]、 Barber等[17]、 Kleine等[18]、 Sheridan等[19]采用镜像模型法, 巧妙地消除了风洞中静止地面边界层的影响, 对尖劈和子弹等简化构型在不同离地高度、 来流速度下的超声速近地流场进行了实验。研究发现, 当离地高度较小时, 飞行器前缘上部呈现为脱体弓形激波, 而下部因局部地面效应呈现为驻定正激波。除风洞实验外, Purdon等[20]通过对比实弹射击和风洞实验结果, 研究了静止地面对子弹超声速近地流场的影响。在数值模拟研究方面, Oliviu等[21]研究了圆柱体近地流动中的激波反射和尾涡结构。Gao等[22]研究了跨声速地面效应下激波-边界层干扰导致的压力脉动和抖振现象。陈晓东等[23]研究了磁悬浮助推发射装置的气动特性并进行了风洞缩比实验。肖虹等[24]计算了Ma=0.1~2.0范围内某钝头体火箭橇实验中的地面效应干扰。王伟等[25]针对细长体开展了Ma=2.5下不同攻角以及不同离地高度的地面效应研究。Yu等[26]进一步研究了乘波体构型在复杂地面构型下的地面效应流场和气动特性。与上述静态地面效应不同, 助推加速引起的非定常地面效应更为复杂多变[27], 常伴随流场结构非定常转变和气动载荷非线性时变, 并出现双解问题和迟滞现象[28-30]。针对非定常地面效应流动机理的研究尚处于起步阶段, 仍待深入研究。
气动弹性及稳定性问题在电磁发射中同样不可忽略。已有研究主要关注气动力-结构弹性力构成的经典弹性系统。例如, Nuhait等[31]、 Dessi等[32]研究了二维翼型在地面效应下的颤振特性, 结果表明地面效应具有使翼型失稳的作用。张斌等[33]通过涡诱导的圆柱自由振荡算例和二维颤振标模, 研究了地面效应对气动弹性动态响应和颤振边界的影响。此外, 电磁弹性力的引入将使得气动弹性问题更加突出、 独特和复杂。
为突出重点和分解难点, 本文基于逐步解耦的思路, 选取NACA0012典型二维翼段作为研究对象, 对电磁弹性力-气动力耦合作用下的翼段加速地面效应进行研究, 重点关注翼段加速过程中的流场、 姿态和气动载荷的演变规律, 同时考察弹性系统参数对电磁助推稳定性的影响。
1 气动-电磁耦合模型和数值计算方法
1.1 物理模型和控制方程
图1为考察的二维NACA0012翼段示意图。坐标系原点O与翼段质心初始位置重合,X轴沿水平方向, 与电磁推进方向相反;Y轴沿铅垂方向, 竖直向上;Z轴由右手法则确定。翼段上下型线对称, 弦长l为1.0 m, 质心距离翼前缘0.4 m, 俯仰角为体轴与X轴夹角, 规定抬头为正, 简记为θ, 初始时刻θ=θ0。单位展长翼段质量为82.0 kg, 转动惯量I为11.4 kg·m2。
电磁悬浮系统的地面模组内置于地面, 翼段通过预先布置于A,B两处的磁体与地面模组感应产生电磁悬浮力, 从而悬浮于平面轨道上。质心离地悬浮高度为h, 初始时刻h=0.5 m。电磁悬浮力与悬浮高度相关。悬浮力可简化为位于翼段上A,B两点的“弹簧振子”。弹簧刚度k0与电磁悬浮刚度一致, 为150 kN/m。翼段以加速度a=100 m/s2向左匀加速运动, 并保留沿Y向平动和绕Z轴转动。
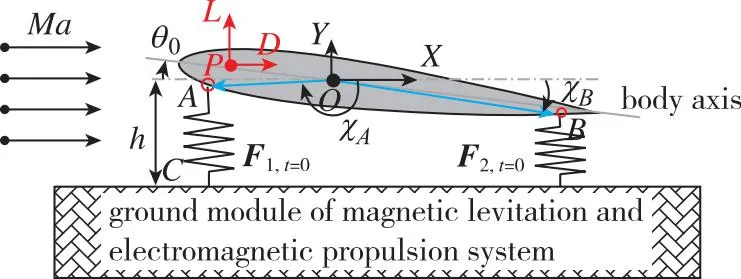
(a) Initial time

(b) Some time图1 电磁助推NACA0012翼段受力示意图Fig. 1 Schematic diagram of force analysis of the NACA0012 wing accelerated by electromagnetic propulsion
对于存在运动边界(即翼段)的非定常数值模拟, 采用任意Lagrange-Euler形式的流动控制方程求解。在控制体V内, 积分形式的质量守恒、 动量守恒和能量守恒方程通式为

(1)
式中,ρ是气体密度; ∂V代表控制体边界;A是网格面矢量;φ=(1,ui,T)是通用变量, 其中,i=1, 2, 3;u=uj是速度矢量, 其中,j=1, 2, 3;us=(us1,us2,us3)是网格运动速度矢量;Γ=(0,μ,kT/cp)是广义扩散系数;Sφ=(0, ∂p/∂xi+Si,ST)是广义源项。其中,μ是动力黏度,kT是流体传热系数,cp是比热容,p是静压,T是温度,Si是动量方程源项,ST是能量方程黏性耗散项。为封闭上述方程, 引入理想气体状态方程p=ρRT, 其中,R是摩尔气体常数。
上述方程中, 位于运动物体表面的us项须通过求解电磁弹性力-气动力耦合的动力学方程组获得。为建立动力学模型, 以下对电磁弹性力进行建模, 并给出电磁弹性力-气动力耦合受力模型。
对图1中翼段进行简要受力分析。翼段受气动阻力D和气动升力L作用, 二者对质心产生气动力矩Mair=-OP×(L+D), 其中P点为气动压心。此外, 电磁悬浮力F1,F2分别对质心产生电磁力矩M1,M2。规定电磁悬浮力、 气动力与X,Y轴正方向一致为正, 电磁力矩和气动力矩抬头为正。则有
F1(t)=-k(yA-yA0)+F1,t=0
(2)
F2(t)=-k(yB-yB0)+F2,t=0
(3)
M1(t)=-OA×F1
(4)
M2(t)=-OB×F2
(5)
式中, 等号第2项F1,t=0和F2,t=0表示求解初始时刻弹簧振子A,B具有的Y向初始电磁悬浮力。
因此,绕翼段质心的刚体动力学二自由度控制方程为
(6)
(7)

对上述矢量方程进行标量化处理, 则电磁悬浮力F1,F2为
F1=-k(yA-yA0)+F1,t=0
(8)
F2=-k(yB-yB0)+F2,t=0
(9)
式中,yA,yB分别是任意时刻A,B点的Y向坐标。由刚体运动关系,yA,yB可由O点平动位移y和相对O点的转动位移给定。以图1中B点为例
(10)
yB=y-|OB|sin(χB+Δθ)
(11)
式中,χB是初始时刻由质心水平单位正矢量顺时针转动至与OB共线时的几何夹角, 值域为[0, π]。Δθ是相对于初始时刻的俯仰角变化量。同理
(12)
yA=y-|OA|sin(χA+Δθ)
(13)
进一步地, 将式(8)~(13)代入式(6)、 (7)可得弹性系统控制方程的标量一般形式
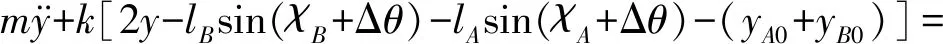
(14)
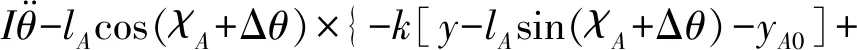
(15)
式中,lA和lB表示A,B弹簧作用点与质心的距离, 即lA=|OA|,lB=|OB|。
本文考察相对理想化的初始状态, 假定磁体A,B均位于体轴上,lA=0.4 m,lB=0.6 m, 磁体间距l0=lA+lB=1.0 m, 翼段初始俯仰角θ0=0, 则有yA0=yB0=0,χA=π,χB=0,Δθ=θ; 同时假定弹簧初始处于松弛状态, 则F1,t=0=F2,t=0=0。则式(14)、 (15)可写为
(16)
(17)
对于以上弹性系统, 图2给出了电磁弹性力-气动力-惯性力耦合作用下的翼段近地加速非定常分步求解策略。

图2 翼段加速过程非定常求解策略Fig. 2 Unsteady solution strategy for wing acceleration
1.2 网格和计算方法
翼段近地加速过程的计算域如图3所示。计算域的入口及出口均采用压力远场边界条件, 并设置在远离翼段10倍弦长距离以外。时变来流的Mach数为Ma=0~1.5, 压力为1 atm(1 atm=1.013 25×105Pa)、 温度为288.15 K。翼段和地面满足黏性无滑移绝热边界条件, 地面速度与来流速度一致。

图3 计算域及边界条件Fig. 3 Computational domain and boundary conditions
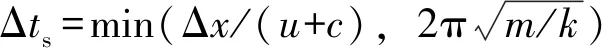

图4 翼段邻域的重叠网格Fig. 4 Overset grids around the NACA0012 wing
为了考察网格无关性, 对来流Mach数Ma=0.8条件下不同网格尺度下NACA0012翼段定常气动力进行了对比。其中, 较稀疏网格数为1.4×105(流向网格尺度10 mm), 中等尺度网格数为2.7×105(流向网格尺度5 mm), 较密集网格数为1.12×106(流向网格尺度3 mm)。结果表明, 随着网格数量的增加, 阻力、 升力和力矩均趋于收敛, 本文选取中等尺度网格开展研究。
1.3 计算方法验证
在跨/超声速阶段, 激波干扰和激波-边界层干扰是典型的地面效应流动特征。采用Doig风洞实验结果[11], 对本文数值方法模拟地效的有效性进行了验证。实验来流条件为Ma=2.4,Re=3.07×105,α=0°, 地面效应采用固定壁板方式模拟。在相同条件下开展了数值模拟, 图5给出了数值纹影和子弹表面压力系数分布。为了更加直观地对比地面效应波系的位置及形态, 这里将数值纹影与实验纹影对称放置。可见, 数值与实验结果吻合较好, 对激波捕捉的位置相近。
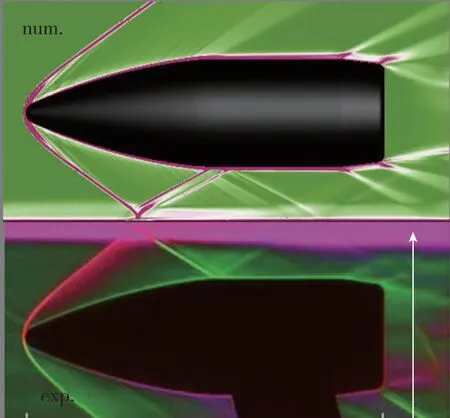
(a) Schlieren photograph
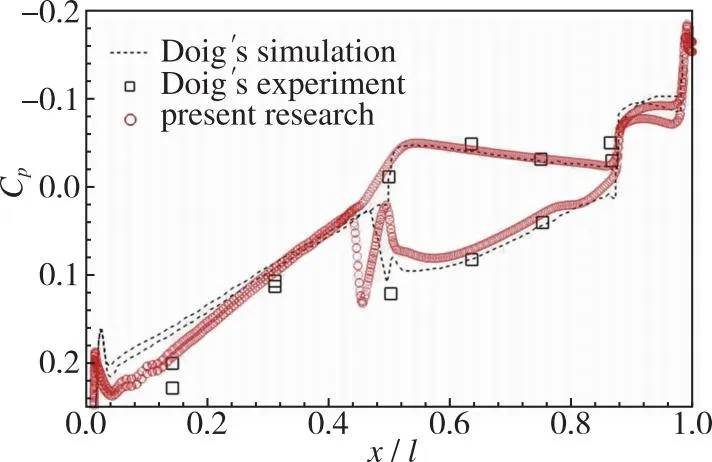
(b) Surface pressure distribution 图5 超声速子弹地面效应的数值与实验对比, Ma=2.4Fig. 5 Comparison of ground effects of the supersonic projectile between numerical and experimental results, Ma=2.4
进一步地, 采用AGARD提供的NACA0012跨声速简谐振荡实验[24]对非定常数值方法开展了验证。翼型的振荡形式如下
α(t)=α0+αmsin(ωrt)
(18)
式中,α0为平均来流攻角,αm为振荡幅值,ωr为角频率。图6给出了NACA0012跨声速简谐振荡抬头上仰α=2.34°时刻的数值与实验压力系数分布对比结果。数值计算获得的压力分布与实验数据吻合良好, 说明本文数值方法对含运动边界的动态俯仰模拟具有较高精度。
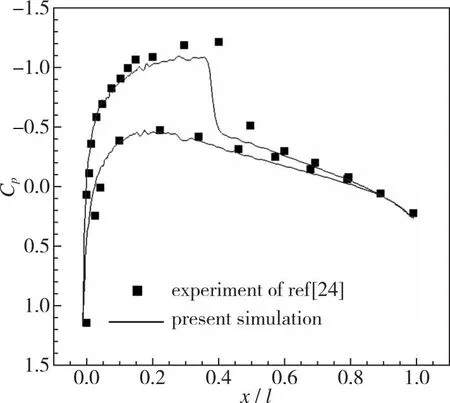
图6 攻角α=2.34°姿态时翼段压力系数分布Fig. 6 Pressure coefficient distribution on the wing surface, α=2.34°
2 结果与讨论
本节首先对二维NACA0012翼段在相对悬浮高度为h/l=0.5下的典型加速地面效应进行研究, 以厘清近地流场、 翼段姿态和气动载荷的演变规律, 而后考察翼段悬浮高度、 悬浮刚度、 悬浮磁体间距3个关键因素对电磁助推加速稳定性的影响。
2.1 翼段加速地面效应及气动力特性
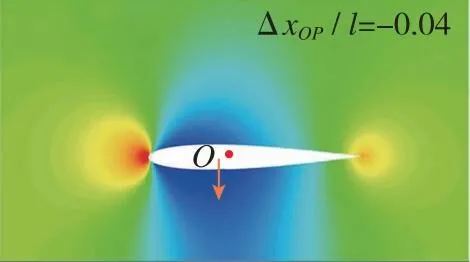
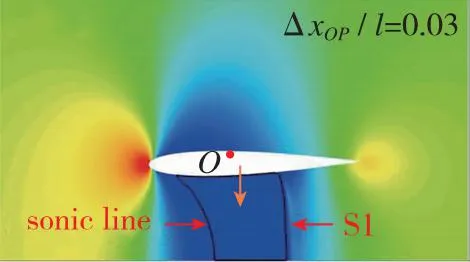
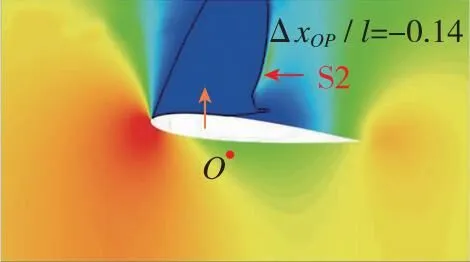
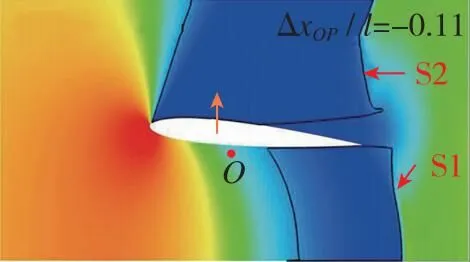
翼段近地电磁悬浮推进过程中的典型时刻加速流场变化如图7所示。为了便于分辨各流场中翼段相对初始位置的沉浮位移和姿态, 在图7中标识O点以显示初始时刻翼段质心位置。由于弹簧振子在初始时刻处于完全松弛状态, 所以也可由沉浮位移判断电磁悬浮力的方向。同时, 在图7中标识箭头位置和方向以表示压心位置和升力方向,ΔxOP/l为质心指向压心的流向距离与弦长的比值, 正值则表示压心在质心右方。图7表明, 翼段在加速过程中的流场结构和受力特性复杂多变, 根据速域可大致分为4个阶段。

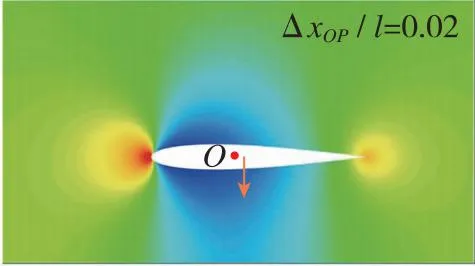
(a) Ma=0.40
(b) Ma=0.50

(c) Ma=0.60
(d) Ma=0.70
(e) Ma=0.76

(f) Ma=0.80
(g) Ma=0.86
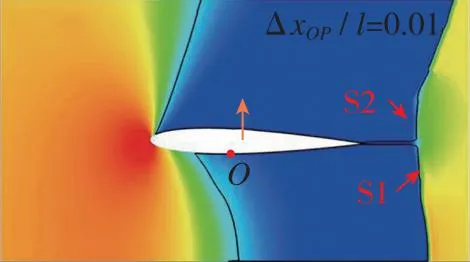
(h) Ma=0.90

(i) Ma=1.00

(j) Ma=1.10
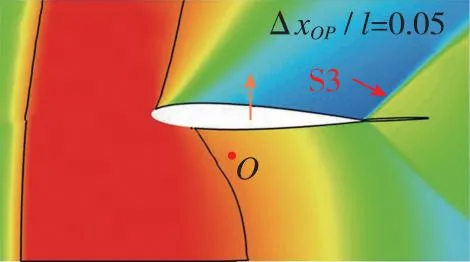
(k) Ma=1.30
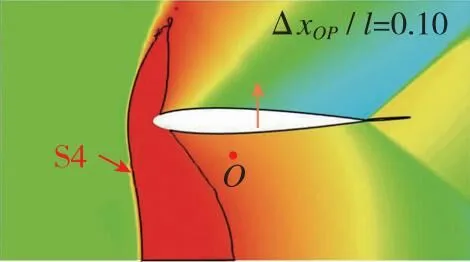
(l) Ma=1.50
第1阶段, 当Ma≤0.60, 上下翼面呈现亚声速流动。自由空间内上下翼面流动基本对称, 压心位置近似与质心重合, 翼段姿态相对稳定。而受地面效应影响, 上下翼面流动逐渐出现差异, 下翼面低压区迅速增大, 出现局部超声速区域(图7(c)), 翼段压心前移(向左移动)并受到负升力, 因此翼段下沉并低头。
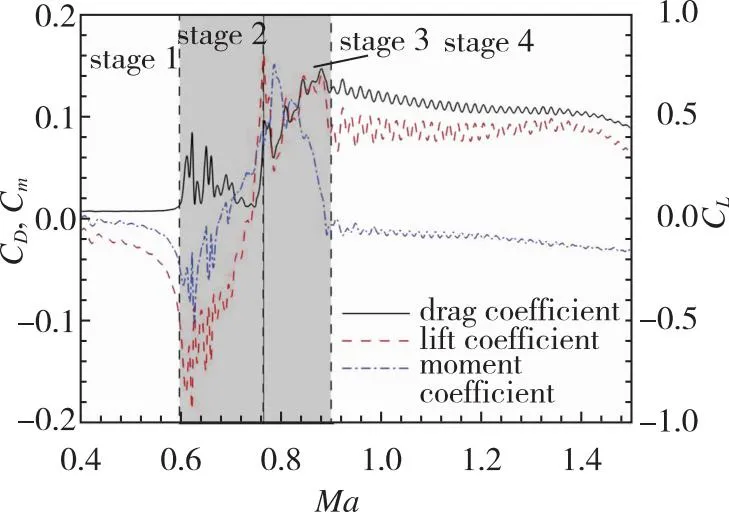
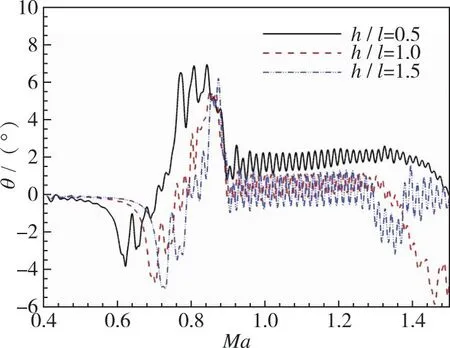
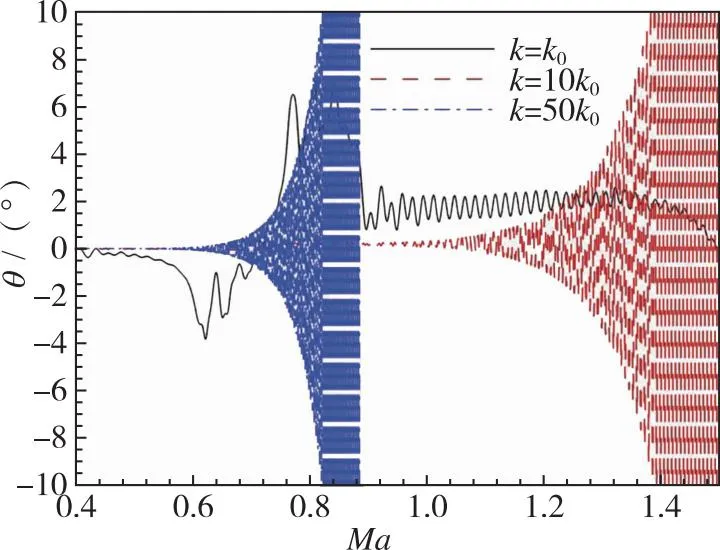
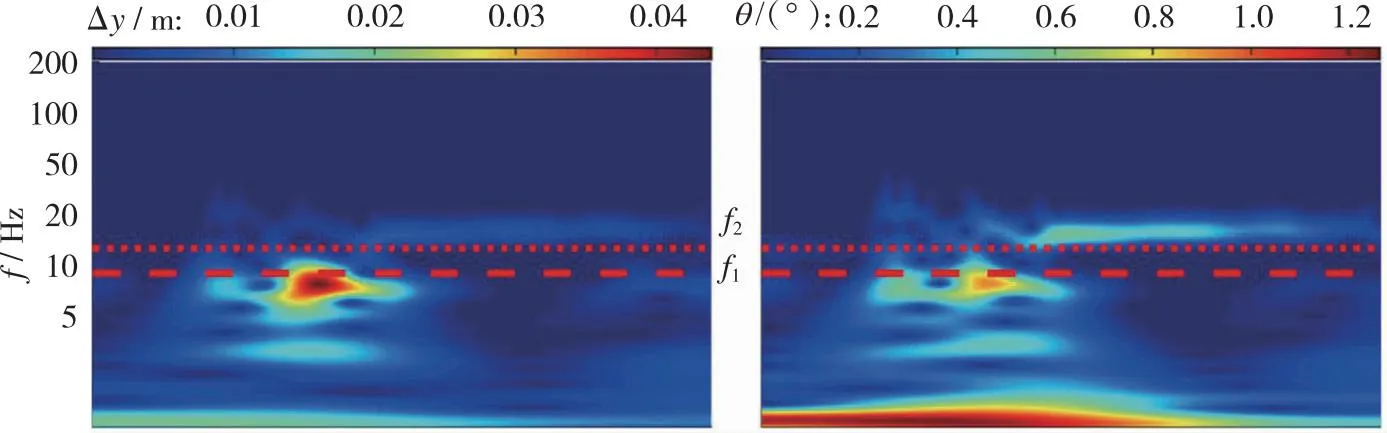
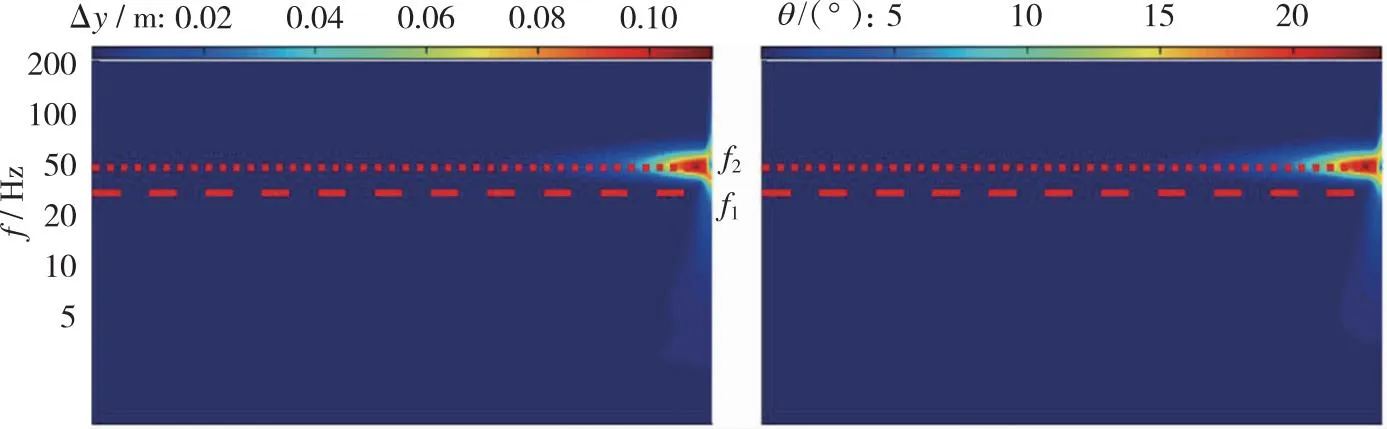
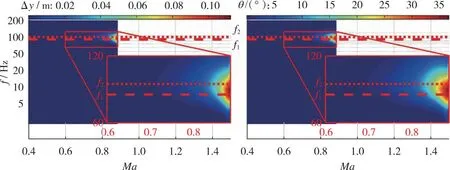
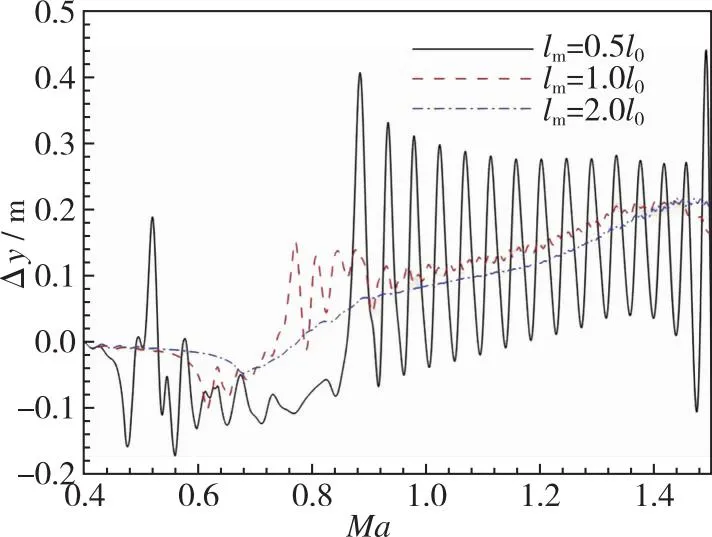
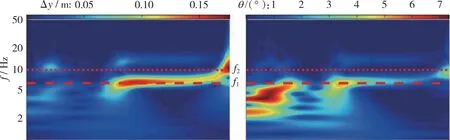
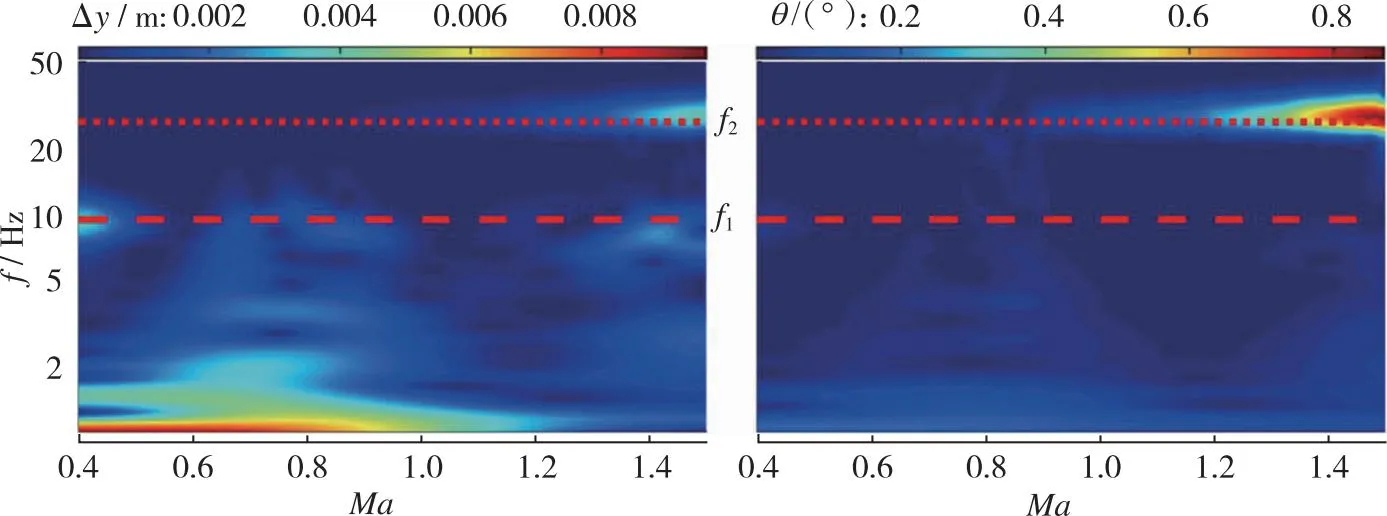
第2阶段, 当0.60 第3阶段, 当0.76≤Ma<0.90, 上翼面保持跨声速流动特点, 以局部超声速低压膨胀区和其后的恢复激波S2为主要特征, 随着来流速度增加, S2逐渐后退, 尾部斜激波S3形成。在电磁拉力作用下, 翼段开始下降, 下翼面重新建立起壅塞, 与第2阶段壅塞流动不同的是, 此时激波S1已完全退出下翼面, 流动处于完全膨胀状态。因此壅塞再现是第2阶段向第3阶段转变的判据。综合第2和第3阶段来看, 流动的非定常特性和壅塞-通流的交替变换引起了翼段的升力方向、 压心位置和悬浮姿态显著变化, 对其运行稳定性影响明显。 第4阶段, 当0.90≤Ma<1.50, 上翼面呈现出完全超声速流动, 以此为标志流动开始进入第4阶段; 下翼面持续保持壅塞, 处于完全膨胀状态。当来流处于超声速速域时, 翼段前方压缩波逐渐汇聚成为激波S4并向翼段靠近, 下翼面壅塞流动以前缘脱体正激波为主要特征, 翼段下半部多余流量从翼段前缘溢流口向翼段上半部泄流。该阶段, 翼段受超声速地面效应影响, 压心位置和悬浮姿态相对稳定, 受到正升力和电磁拉力, 翼段上浮。 与流场分析相对应, 图8给出了加速过程中的翼段质心垂向位移和俯仰角的演变曲线。可以看出, 在第1阶段, 质心垂向位移和俯仰角曲线较为顺滑。质心高度不断下降, 最大位移量为-0.1 m, 翼段连续低头, 最小俯仰角约为-3.8°。在第2, 3阶段, 由于气动压心“后移-前移-后移”和升力“负-正”的迅速转变, 该阶段内的质心位移和俯仰角曲线出现明显振荡。特别地, 对于第2阶段, 在下翼面壅塞消失过程中, 原本宽泛的低压区迅速缩小直至消失(图7(e)), 前缘压力得到恢复, 同时前缘上表面局部超声速低压区开始显现, 这一高一低造成翼段整体抬头趋势较明显。而当处于第3阶段, 壅塞再现, 随着上翼面恢复激波S2的后退和低压区的扩大, 上下翼面流动特征趋近并相对稳定, 压心始终位于质心附近, 抬头趋势被抑制, 俯仰角和质心位移整体保持平稳振荡。在第4阶段, 质心位移和俯仰角的平均值先基本不变后略微降低, 曲线的振幅明显减弱但频率明显升高。进一步地, 对助推加速过程中的翼段气动力/力矩系数进行研究, 其中参考面积为Sreff=1 m2。从图9可以看出, 翼段气动载荷变化规律和图8中姿态变化规律相近, 与流场所处阶段具有明显的相关性。 图8 翼段质心位移和俯仰角演变Fig. 8 Evolution of centroid displacement and pitch angle of the wing 图9 翼段气动载荷系数演变Fig. 9 Evolution of aerodynamic force coefficients of the wing 因此, 亚声速地面效应对翼段运行姿态的影响特点可简要总结为基本无振荡; 跨声速地面效应诱导翼段运行姿态低频大幅振荡; 而超声速地面效应诱导翼段运行姿态高频小幅振荡。 2.2.1 气动-电磁弹性系统稳定性讨论 通过前述分析发现, 在跨/超声速运行阶段尤其是第2, 3阶段, 流场变化显著, 翼段受到较强的非定常气动载荷冲击, 表现出大幅度周期性振荡, 容易产生稳定性问题。实际上, 电磁悬浮力可认为是弹性力, 这与传统的气动力-结构弹性力所构成的气动弹性问题类似。因此, 本节从方程相似角度对悬浮加速运行稳定性进行分析。 无外力干扰下的经典二元翼段弹性体颤振控制方程[34]分别由质心动力学方程和绕动点刚心E的转动方程建立, 可写为 (19) (20) 式中, 广义坐标yE和θE分别是弹性体刚心的沉浮位移和绕刚心的俯仰角;IE表示绕刚心转动惯量;xa为质心与刚心距离且质心位于刚心后方;CyE和CθE分别为翼段弹性体刚心沉浮和俯仰阻尼系数;Mair是对质心的气动力矩;KyE和KθE分别为翼段弹性体沉浮和俯仰刚度系数; 两式等号右边QyE和QθE分别对应刚心气动升力和刚心气动力矩。 相较之下, 虽然本文所考察的电磁弹性力-气动力系统(式(16)~(17))暂不考虑结构弹性和结构阻尼, 即已略去与xa和结构阻尼有关的量, 但由于有电磁外部力的约束且不显含广义坐标θ, 也具有一定复杂度。特别地, 在小攻角振荡假设下, 式(16)~(17)可改写为 (21) (22) 将式(19)~(20)与式(21)~(22)对比, 不难发现, 由电磁弹性力-气动力耦合模型推导出的弹性动力学控制方程与经典气动弹性控制方程形式类似。主导电磁悬浮近地加速系统的不稳定性因素主要存在3项。一是悬浮高度h, 该项直接影响地面效应和相关气动载荷, 即方程等号右边的升力项L和力矩项Mair。二是悬浮刚度k, 其直接影响了系统的刚度。三是悬浮磁体间距, 由lA和lB决定。以下分别对悬浮高度、 悬浮刚度和磁体间距对系统稳定性的影响开展研究。 2.2.2 悬浮高度对系统稳定性的影响 控制磁体间距和悬浮刚度不变, 研究了不同初始相对悬浮高度h/l=0.5, 1.0, 1.5对系统稳定性的影响。图10给出了不同相对悬浮高度下翼段近地加速过程中质心位移和俯仰角演变曲线。可以看到, 当增加悬浮高度, 由于下翼面阻塞度减小, 流动产生壅塞所需的Mach数增加, 地面效应减弱, 因此第1阶段向第2阶段的转变Mach数明显延后, 但质心位移和俯仰角曲线的振荡幅度在不同悬浮高度下仍基本一致。此外, 不同悬浮高度下, 第3阶段向第4阶段转变的阈值基本不变。这主要是由于第3向第4阶段转变的标志是恢复激波S2退出上翼面, 而不同离地悬浮高度下上翼面流动特征基本一致。 (a) Centroid displacement (b) Pitch angle 上述结果表明, 增加悬浮高度能够缩短跨/超声速地面效应气动激励的作用时间。并且, 翼段在第4阶段的质心垂向高度下降更快, 俯仰角曲线振荡的平均值基本趋于0°攻角, 但振幅略有增加。从系统稳定性来看, 适当增加悬浮高度有利于减弱地面效应, 从而提高系统稳定性。但考虑到工程可实现性, 悬浮高度的可调节范围受诸多限制, 对于实际工程应做进一步讨论。 2.2.3 悬浮刚度对系统稳定性的影响 控制悬浮高度和磁体间距不变, 通过在悬浮刚度k0基准上依次扩大10倍和50倍, 研究不同悬浮刚度下的系统稳定性。图11给出了悬浮刚度k=k0, 10k0, 50k0下翼段近地加速过程中质心位移和俯仰角演变曲线。 图11表明, 当增加悬浮刚度至10k0, 50k0时, 在加速前期阶段, 翼段的质心沉浮位移和俯仰角的振荡幅度能够被有效抑制, 位移振荡范围均限制在±10 mm区间。但较大的悬浮刚度反而导致翼段更高频的振荡, 直至发散, 其中俯仰角最大值约40°, 远远超过失速迎角, 严重破坏了系统稳定性。并且, 悬浮刚度50k0相比10k0工况的发散更加提前, 出现在亚声速域。 (a) Centroid displacement (b) Pitch angle图11 不同悬浮刚度下翼段加速质心位移和俯仰角演变Fig. 11 Evolution of centroid displacement and pitch angle of the wing at different suspension stiffness 为解释系统发散现象, 进一步地, 对不同悬浮刚度下翼段加速过程中的沉浮位移和俯仰角进行时频分析。图12给出了加速过程中各频率翼段沉浮及俯仰运动随Mach数变化的能量分布。其中, 红色区域表征翼段运动能量集中频率, 红色长虚线和短虚线分别表示无气动激励下翼段自由振荡的1阶及2阶固有频率。 可见, 当悬浮刚度为k0时, 翼段沉浮与俯仰运动的频率均偏离自由振荡系统固有频率。翼段的运动主要受到气动力/力矩周期性脉动激励。随着Mach数增大, 气动激励由亚声速阶段的简单低频激励(约1 Hz)发展为跨声速阶段的复杂低频激励(1 Hz与8 Hz共存); 在超声速阶段, 激励频率进一步升高, 并引发系统以高于2阶固有频率的振动(20 Hz左右)。当悬浮刚度增大至10k0时系统悬浮刚度加强, 悬浮力足以克服亚跨声速阶段的气动激励, 但随着固有频率升高, 气动激励与系统2阶模态发生耦合, 加之悬浮系统阻尼不足, 诱发系统以2阶特征频率发生颤振式的不稳定振动。当悬浮刚度增大至50k0时, 系统1阶与2阶固有频率进一步升高并趋近, 气动激励同时与1阶、 2阶模态发生耦合, 从而诱发系统提前在Ma=0.8时发生不稳定振动。 从另一方面讲, 若减小电磁助推加速的目标速度至系统发散前(如Ma=1.2), 限定系统悬浮刚度k0 2.2.4 悬浮磁体间距对系统稳定性的影响 控制悬浮高度和悬浮刚度不变, 进而研究不同悬浮磁体间距下(lm=lA+lB=0.5l0, 1.0l0, 2.0l0)的系统稳定性。式(16)~(17)表明, 增加磁体的前后纵向间距, 可以增大电磁悬浮力的力臂, 从而增加系统的俯仰刚度。图13给出了不同磁体间距下翼段近地加速过程中质心位移和俯仰角演变曲线。结果表明, 增加悬浮磁体间距, 能够大幅抑制加速过程中的质心沉浮位移和俯仰角的振荡幅度, 但翼段在第4阶段的振荡频率略有升高。减小悬浮磁体间距, 翼段出现明显沉浮和俯仰振荡的速域提前, 并表现为低频大幅振荡。 (a) k=k0 (b) k=10k0 (c) k=50k0图12 不同悬浮刚度下翼段加速质心位移和俯仰角时频分析Fig. 12 Time-frequency analysis of centroid displacement and pitch angle of the wing at different suspension stiffness (a) Centroid displacement (b) Pitch angle 同样地, 对不同悬浮磁体间距下翼段加速过程进行时频分析, 如图14所示。可见, 减小悬浮磁体间距至0.5l0时, 系统的俯仰刚度减小。系统在亚声速阶段的主要振动为俯仰运动, 沉浮与俯仰运动频率随Mach增大由3 Hz提升至约5 Hz。进入跨声速阶段后, 翼段主要振动为沉浮运动, 振动频率与系统1阶固有频率一致。进入超声速阶段后, 翼段振动频率由1阶固有频率过渡至2阶固有频率, 且存在气动力激励与固有频率耦合进而诱发颤振式发散的风险。当悬浮磁体间距增大至2.0l0时, 在Ma=0.4~1.2阶段, 翼段振动受沉浮运动主导, 表征为1 Hz左右的低频, 而俯仰运动受到明显抑制。但在Ma>1.2后, 翼段的主要运动由沉浮转变为俯仰运动, 气动激励与系统的2阶模态振动发生耦合, 若继续加速(Ma>1.5), 可能存在诱发不稳定性的风险。因此对于目标发射速度Ma=1.5来讲, 增加磁体间距仍在安全性前提下有利于提高系统稳定性。 (a) l=0.5l0 (b) l=1.0l0 (c) l=2.0l0图14 不同悬浮磁体间距下翼段加速质心位移和俯仰角时频分析Fig. 14 Time-frequency analysis of centroid displacement and pitch angle of the wing at different spacing between suspension magnets 以NACA0012二维刚性翼段为研究对象, 建立了电磁力-气动力-惯性力耦合数理模型, 对翼段加速地面效应开展了研究, 厘清了翼段Ma=0~1.5加速过程中流场、 姿态和气动载荷的演变特性, 探究了悬浮高度、 悬浮刚度、 磁体间距对电磁助推稳定性的影响。主要结论如下: 1) 翼段在加速过程中的近地流场结构复杂多变, 根据速域可大致分为4个阶段。第1阶段, 当Ma≤0.60, 上下翼面呈现亚声速流动。第2阶段, 当0.60 2) 翼段运行姿态和气动载荷变化规律与流场所处阶段或者速域具有明显的相关性。在第1阶段, 亚声速地面效应对翼段运行姿态和气动载荷的影响特点可简要总结为基本无振荡。在第2, 3阶段, 跨声速地面效应诱导翼段运行姿态和气动载荷低频大幅振荡。在第4阶段, 超声速地面效应诱导翼段运行姿态和气动载荷高频小幅振荡。 3) 电磁助推稳定性与悬浮高度、 悬浮刚度和磁体间距有关。增加悬浮高度能够缩短跨超声速地面效应气动激励的作用时间, 有利于一定程度上提高系统稳定性; 增加悬浮刚度显著抑制了系统振幅, 但需限定电磁助推目标速度小于系统振荡发散临界Mach数; 增加磁体间距能有效提高系统稳定性, 但在更高Mach数运行速域内存在气动激励与固有频率耦合的发散风险。
2.2 翼段稳定性分析




3 结论
