反应性射流中湍流/非湍流界面附近标量输运特性

曹晴晴, 李 岩, 张欣羡, 周 毅

(1. 南京理工大学能源与动力工程学院, 江苏南京 210094; 2. 中国航天空气动力技术研究院, 北京 100074;3. 北京航空航天大学流体力学教育部重点实验室, 北京 100191)

引 言

射流具有较强的输运和混合能力, 因此在工业领域应用非常广泛, 例如空气送风系统, 燃油喷射系统和液体喷洒、 喷涂和切割等。射流的一个典型特征是流场中存在着清晰的、 薄层包裹着的湍流区域, 使其与无旋区域(非/低湍流区)分开, 该薄层控制着无旋区域和湍流区域之间能量、 动量和标量的运输和交换[1], 称为湍流/非湍流界面层。

国内外学者针对T/NTI层的几何特性[2-4]和动力学特征[5-7]开展了广泛的研究。李思成等[2]通过在流场中安装垂直于流向的扰流板研究脱落涡对T/NTI层沿流向的影响, 发现在扰流板影响下T/NTI的分形维度减小, 表明脱落涡使T/NTI层多尺度特性、 三维性呈减弱的趋势。张爽等[4]通过实验发现二维、 三维密度界面存在分形结构, 并且随着湍流强度的减弱, 物质之间的混合过程在减缓, 密度界面也变得更加光滑。Hayashi等[8]研究时间演化下平面射流的剪切运动和T/NTI层之间的关系, 发现湍流核心区和T/NTI层中剪切层的速度跃变大约是Kolmogorov速度尺度的7倍, 且界面附近的剪切层大部分平行于T/NTI层。Nagata等[9]通过计算界面局部坐标系下的统计量研究T/NTI层附近的流动特性, 发现T/NTI层附近的内能变化率与射流的初始动能成正比, 无旋边界的内能变化由扩散/膨胀效应造成, 压缩性通过影响T/NTI层的总表面积影响总卷吸速率。Watanabe等[10]基于Burgers涡旋模型探究T/NTI层附近孤立涡旋的作用, 发现在涡量场上的应变率使非湍流流体朝向无旋边界移动, 与涡量场相关的速度将之卷吸进入湍流核心区。

射流往往也伴随着不同组分的化学反应[11,12]和标量输运[13,14], 学者们对射流中的化学反应和标量输运开展了丰富的研究, 包括组分浓度比[15]、 化学反应速率[16]等因素对标量输运的影响等。王芳等[17]利用小型流化床射流装置研究预氧化反应后的生成物分布、 半焦化物质的结构与活性, 得出温度、 反应物浓度比例和当量空气系数对半焦化的影响。李岩等[18]通过研究不同射流口间距下双射流间的流动-化学反应耦合过程, 发现在双平行反应性射流标量场中化学反应标量输运方程各项所控制的对流、 扩散作用和化学反应对标量产生、 消耗和输运的影响以及射流相互作用尺度在该流场中的适用性。Watanabe等[19]针对反应性流动提出了一种基于近似反卷积模型的大涡模拟方法, 并将之与粒子追踪技术相结合, 模拟具有二级基元反应的平面射流, 验证了该混合模型预测反应标量统计特性的可行性和准确性。

他人对反应性平面射流、 流场中的T/NTI层、 标量输运分别进行了大量的研究, 但反应性射流流场中T/NTI层附近的传质机理尚不明晰, 缺少针对T/NTI层附近因化学反应和标量输运导致的各组分产生、 消耗、 输运和混合过程的研究。平面单射流作为一种典型的自由剪切流, 研究反应性平面单射流中T/NTI附近的卷吸特性、 化学反应特性、 标量的输运和混合特性, 对于丰富射流的研究内涵, 拓展相关工业的应用领域具有重要的意义。因此本文对射流与环境流之间发生的二级非平衡基元反应进行数值模拟, 研究T/NTI层附近射流与环境流之间发生的化学反应以及标量的产生、 消耗和输运特性。

1 数值方法

1.1 流场和标量场计算

本文基于开源软件OpenFOAM平台中用于解决瞬态不可压缩流场非稳态问题的pimpleFoam求解器。求解器不使用任何湍流模型(设置为laminar), 利用准直接数值模拟[20]方法通过对不可压缩的Navier-Stokes方程组(包含连续性方程和动量方程)求解得到速度场, 方程表达如下

式中,u,p,ν,ρ分别代表流体的瞬时速度、 瞬时压力、 运动黏度和密度,t为时间。

化学反应被动标量输运方程是在对流场本身不产生影响的前提下研究标量输运、 消耗和产生的关键方法。假设二级非平衡基元反应(A+B→R)发生在等温条件下, 考虑到化学反应对组分浓度分布和变化速率的影响, 将化学反应作为被动标量输运方程的控制因素。对于组分α(反应物A、 B和生成物R)的标量输运控制方程表达如下

(1)

其中,Γα表示组分α的浓度;Dα表示分子扩散系数, 假设各组分的分子扩散系数相等。式(1)简写为Atα+ATα=DTα+STα, 其中Atα=∂Γα/∂t为非稳态项, 表示流动-化学反应过程中组分α的浓度随时间的变化情况;ATα=∂ujΓα/∂xj为对流项, 表示射流中对流作用对各组分标量输运的影响;DTα=Dα∂2Γα/(∂xj∂xj)为扩散项, 表示射流中扩散作用对各组分标量输运的影响;STα为化学反应源项,STA=kΓAΓB,STB=kΓAΓB和STR=-2kΓAΓB分别表示化学反应对反应物A、 B和生成物R浓度的影响,k表示该反应的反应速率常数。

1.2 计算模型和参数

本文研究射流与环境流之间发生的二级非平衡基元反应(A+B→R), 反应性流场示意图如图1所示, 其中环境流中预混着反应物A, 射流中预混着反应物B。当反应物B沿着宽度为d的狭缝喷射到流场中时, 与环境流中的反应物A接触并发生化学反应, 反应物A和B以及生成物R随着射流向周围环境以及流场的下游输运。

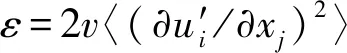
表1 反应性射流数值模拟的几何细节及数值参数

1.3 数值方法验证

本文将反应性射流速度场和标量场的数值模拟结果与他人的实验[24-26]和数值模拟[16,21]结果进行对比, 以验证当前数值方法的准确性。图2是反应性射流无量纲后的平均流向速度和速度脉动均方根的法向分布, 〈u〉C为射流中心线上的平均流向速度,UA为初始平均环境流速度,bU为基于平均流向速度的射流半宽, 是(〈u〉-UA)/(〈u〉C-UA)=0.5时对应的法向坐标。从图2(a)中可以看出在x/d=10, 15和20处射流的速度场具有自相似性, 对应中心线上的Reynolds数分别为1 612, 1 352和1 203, 平均流向速度的法向分布曲线与Gutmark等[24]、 Ramaprian等[25]的实验探究结果和Watanabe等[16]的数值模拟结果非常吻合。从图2(b)中可以看到无量纲后的速度脉动均方根的法向分布与Gutmark等[24]、 Ramaprian等[25]和Stanley等[21]的模拟结果总体上一致, 初始场的不同在一定程度上影响速度脉动均方根的法向分布, 导致了不完全吻合的现象。图2表明平均流向速度和速度脉动均方根的法向分布与他人结果均吻合良好, 验证了速度场模拟的准确性。

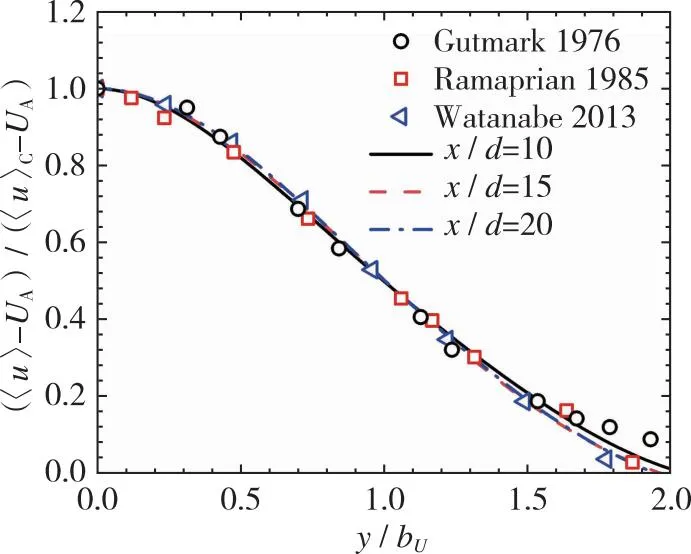
(a) Nondimensionalized mean streamwise velocity

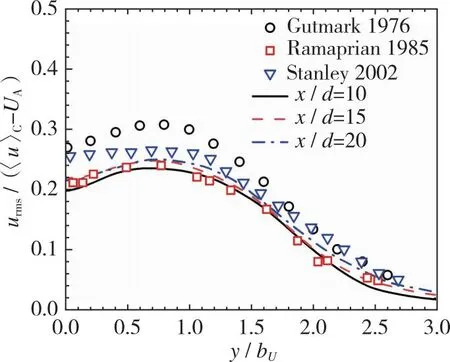
(b) Nondimensionalized RMS values of streamwise velocity fluctuations图2 反应性射流无量纲后平均流向速度和流向速度脉动均方根的法向分布Fig. 2 Nondimensionalized mean streamwise velocity and RMS values of streamwise velocity fluctuations in the normal direction for a reactive jet flow

本文通过验证混合浓度分数沿法向的分布, 以验证化学反应标量场模拟的准确性。在浓度相关计算中, 引入ξ可以提高化学反应与组分混合的计算效率[18], 混合浓度分数ξ为

其中,ξ可看作预混到射流中的非反应性标量[16], 在射流口处为1, 在环境流中为0。根据质量守恒,ΓA/ΓA0+ΓB/ΓB0+ΓR/ΓR0=1, 反应物A和B的瞬时浓度可以通过生成物的瞬时浓度和混合浓度分数获得:ΓA=ΓA0(1-ξ)-ΓR和ΓB=ΓB0ξ-ΓR。

图3是反应性射流无量纲平均混合浓度分数的法向分布, 其中〈ξ〉C表示射流中心线上的平均混合浓度分数,bξ为基于平均混合浓度分数的射流半宽, 即〈ξ〉/〈ξ〉C=0.5时对应的法向坐标。图中可以看出在x/d=10, 15和20处射流的平均混合浓度分数曲线也具有自相似性, 且这些结果与Watanabe等[16,26]的实验结果和数值模拟结果吻合, 由此可以验证标量场模拟的可靠性和准确性。

图3 反应性射流无量纲平均混合浓度分数的法向分布Fig. 3 Nondimensionalized mean mixture fraction in the normal direction for a reactive jet flow

根据Watanabe等[27]在平均流向速度和平均混合浓度分数的测量结果中观察到平面射流自相似区域的典型特征,bξ大于bU, 得出流场中基于平均混合浓度分数的扩散速率应大于预期的平均流向速度。图4是反应性射流分别基于〈u〉-UA和〈ξ〉的半宽bU和bξ的流向分布, 图中证实了上述观点, 且随x/d的增大, 各半宽成比例增大。其中bU和bξ与Watanabe等[26]的数值模拟结果基本吻合。在Watanabe等[26]的数值模拟中, 射流与环境流的初始平均速度与本文不同, 在流场的入口处添加的扰动也是依据实验拟合的脉动速度, 因此导致了两者不完全吻合的现象。

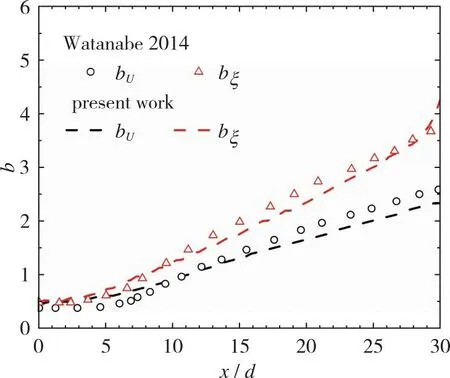
图4 反应性射流基于〈u〉-UA和〈ξ〉的射流半宽的流向分布Fig. 4 Streamwise distribution of a reactive jet halfwidth based on 〈u〉-UA and 〈ξ〉

2 结果分析与讨论

2.1 T/NTI层的识别

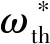
当然，“任务型教学模式”在音乐治疗专业英语课堂实践的过程中，笔者也发现了一些问题，值得在以后的教学中改进。

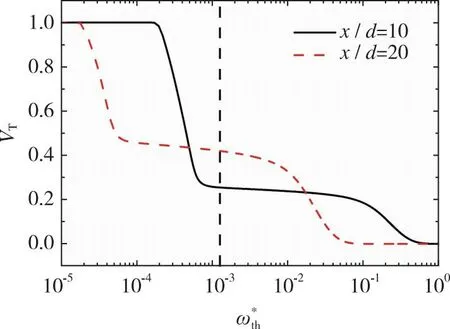
图5 湍流区域的体积分数VT随涡量阈值的变化情况Fig. 5 Change of volume fraction VT in turbulent region with

2.2 流场和标量场可视化

图6是在x/d=10和20处yoz平面上带有无旋边界的瞬时无量纲涡量云图, 其中涡量以ωmax为特征尺度进行无量纲, 白色实线表示T/NTI层的无旋边界, 图中可以看出沿着流向的演化, 射流不断发展, T/NTI层向两侧移动。

(a) Upstream x/d=10 (b) Downstream x/d=20图6 yoz平面上带有无旋边界的瞬时无量纲涡量Fig. 6 Instantaneous nondimensionalized vorticity with irrotational boundary on the yoz plane

图7是反应物A、 B和生成物R分别在x/d=10和20处带有无旋边界的瞬时无量纲浓度云图, 其中环境流中反应物A和射流中反应物B的浓度分别以初始浓度ΓA0和ΓB0无量纲化, 生成物R以其在化学计量比混合物中的最大浓度ΓR0无量纲,ΓR0=ΓA0ΓB0/(ΓA0+ΓB0)[16]。图7中反应物A的浓度由T/NTI层向内逐渐减少, 而上游的反应物B的浓度明显高于下游, 且几乎全部存在于射流内部, 并且随着流场的发展, 生成物R的浓度逐渐增加。这是因为环境流中的反应物A跨越T/NTI层进入湍流区域, 与反应物B接触并发生化学反应, 产生生成物R。随着化学反应的进行, 反应物B的浓度沿流向逐渐减少, 生成物R的浓度逐渐增加。

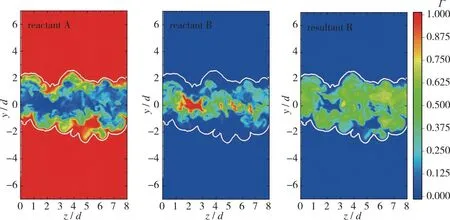
(a) Upstream x/d=10

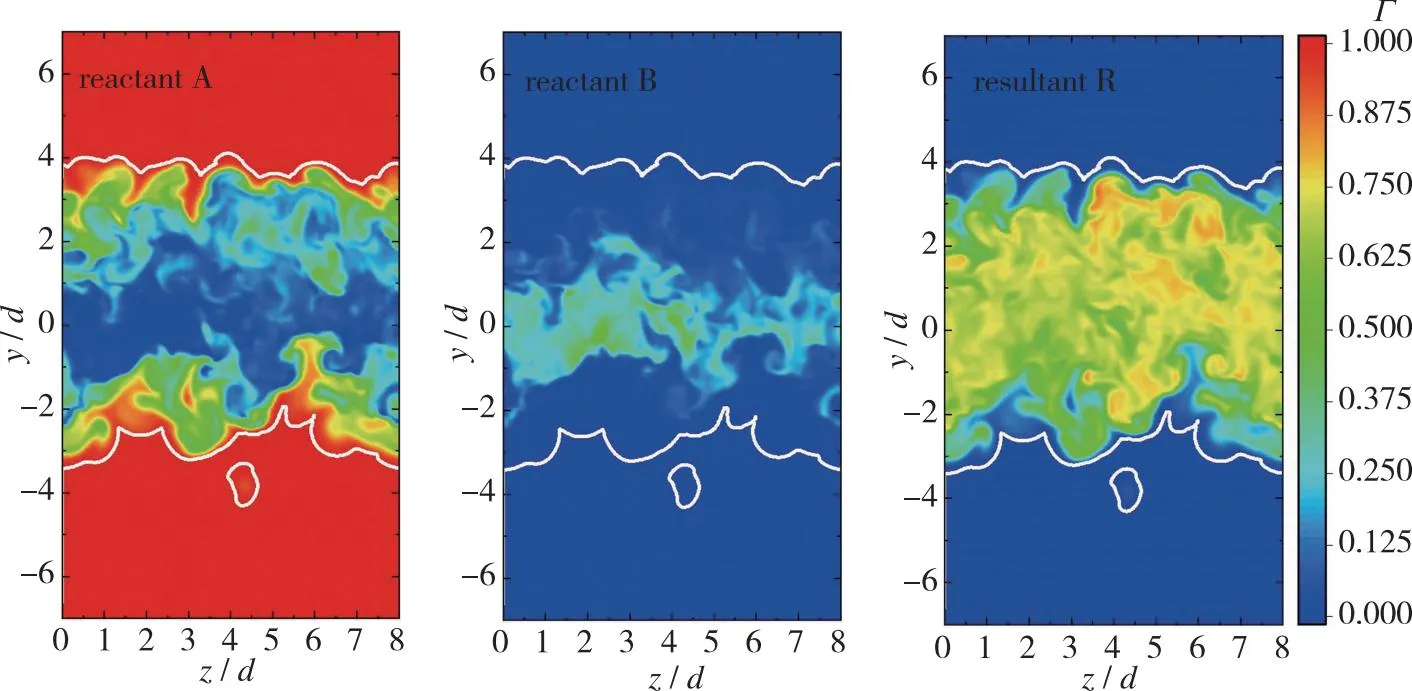
(b) Downstream x/d=20图7 yoz平面上带有无旋边界的反应物A、 B和生成物R的瞬时无量纲浓度Fig. 7 Instantaneous nondimensionalized concentrations of reactant A, B and resultant R with irrotational boundary on the yoz plane

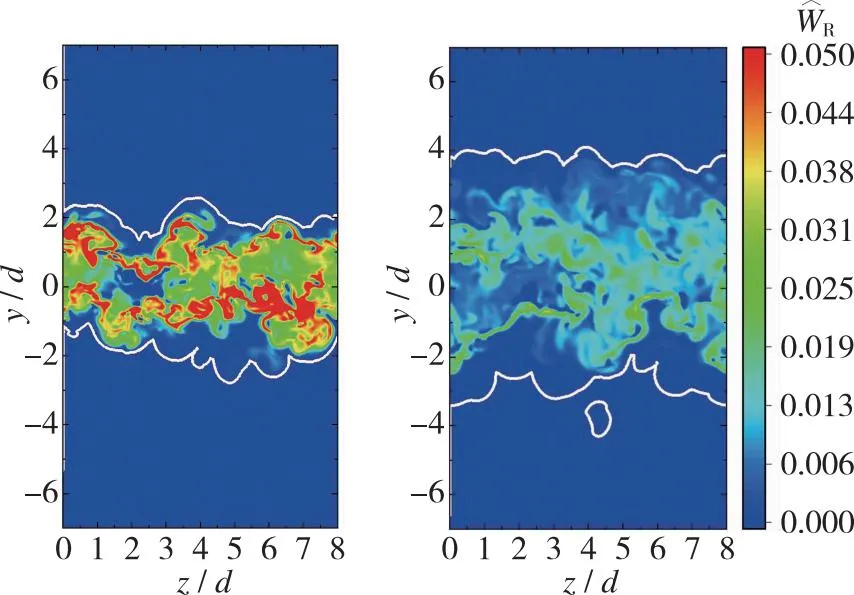
(a) Upstream x/d=10 (b) Downstream x/d=20图8 带有无旋边界的生成物R的瞬时化学反应速率Fig. 8 Instantaneous chemical reaction rate of resultant R with irrotational boundary

2.3 标量产生、 消耗和输运

图9是在x/d=10和20处各组分标量输运方程中各项瞬时值的法向演化, 其中残差项RHS表示式(1)左右两侧的代数差, 垂直虚线表示射流两侧T/NTI层的无旋边界位置。图中RHS在x/d=10和20处的法向演化几乎为0, 这表明标量场的统计结果收敛性良好。在x/d=10处, 各组分的非稳态项Atα和对流项ATα之间几乎呈对称分布, 生成物R的化学反应源项STR和各组分的扩散项DTα的大小相较于非稳态项和对流项较小, 反应物A和B的化学反应源项STA和STB的大小几乎可以忽略。因此可以得出在x/d=10处的湍流区域中对流作用主导各组分的浓度变化, 扩散作用对各组分浓度变化的影响较小, 化学反应使生成物R的浓度少量增加。而在x/d=20处各组分的化学反应源项STα基本为0, 各组分的扩散项DTα值较小, 各组分的非稳态项Atα和对流项ATα之间也几乎呈对称分布。因此可以合理认为在整个自相似区域中, 各组分的浓度变化由对流作用主导, 扩散作用的影响较小, 化学反应几乎不产生影响。

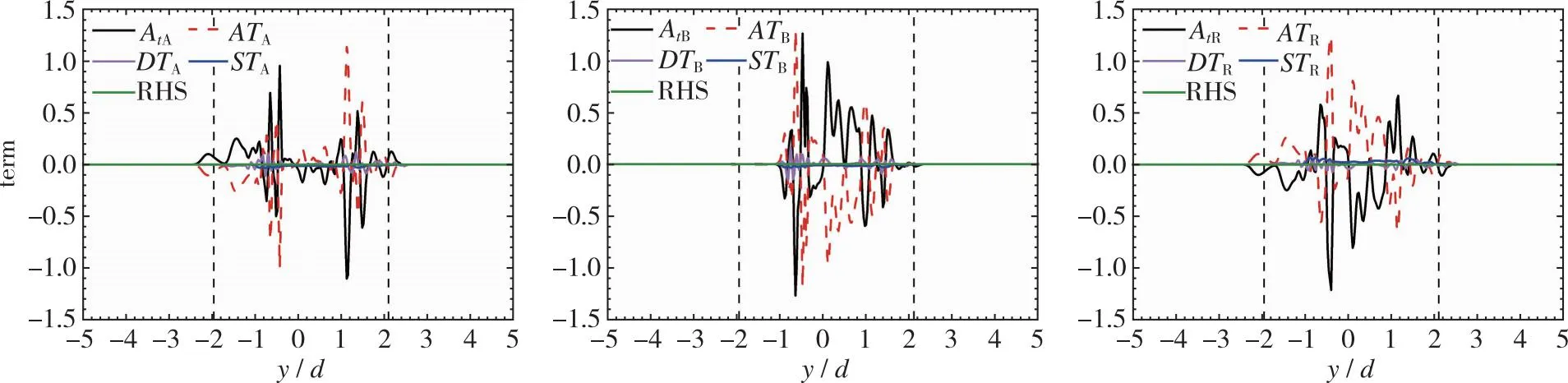
(a) Upstream x/d=10

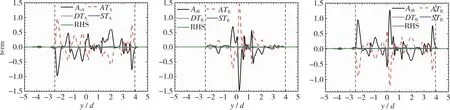
(b) Downstream x/d=20图9 各组分标量输运方程中各项沿中心线的瞬时法向演化Fig. 9 Instantaneous normal evolution of the terms in the scalar transport equation along the center line

2.4 T/NTI层附近的条件平均统计和标量输运特性

在标量输运方程中, 通过对流或扩散的输运作用、 化学反应使组分α的浓度增大的为产生项, 而使组分α的浓度减小的则为消耗项。由公式Atα=-ATα+DTα+STα可知, -ATα>0,DTα>0,STα>0为产生项, -ATα<0,DTα<0,STα<0为消耗项。

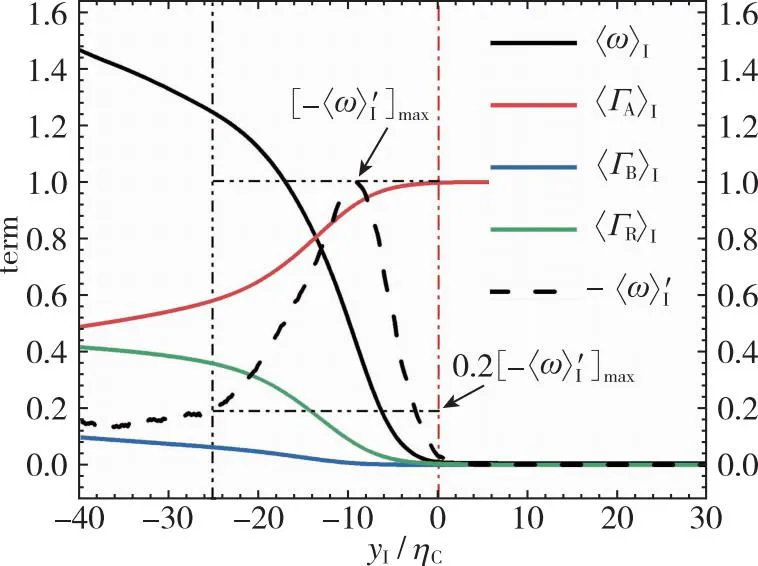
(a) Upstream x/d=10

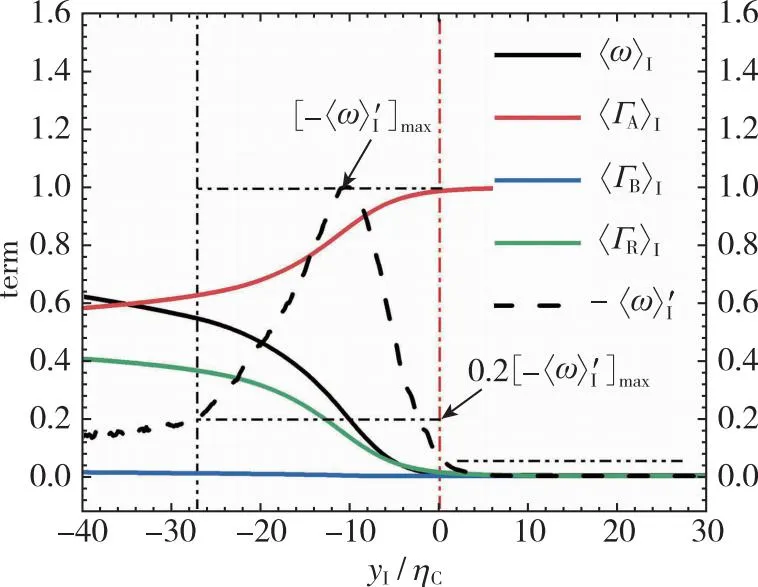
(b) Downstream x/d=20图10 涡量和各组分浓度的条件平均统计Fig. 10 Conditional average of vorticity and concentration of each component

(a) Upstream x/d=10

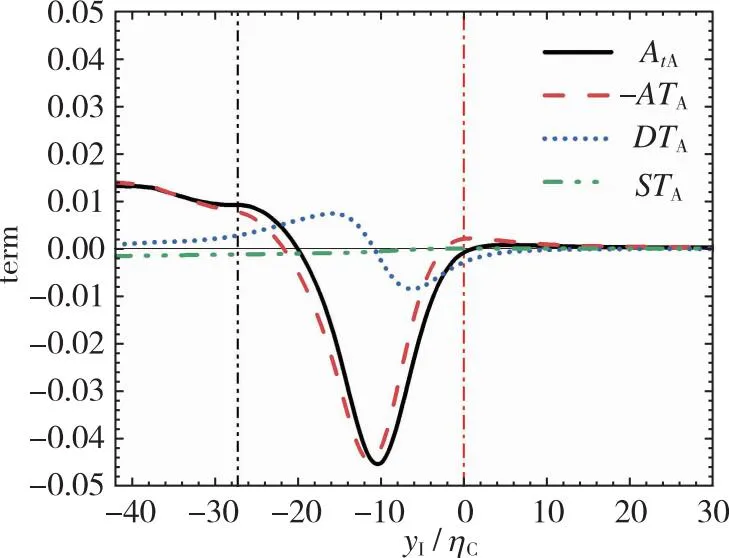
(b) Downstream x/d=20图11 反应物A的标量输运方程中各项在x/d=10和20的条件平均统计Fig. 11 Conditional average of the terms in the scalar transport equation for the reactant A at x/d=10 and 20

图12为反应物B的标量输运方程中各项在x/d=10和20处的条件平均统计。图10中T/NTI层附近反应物B的浓度在x/d=10处较小, 在x/d=20处基本可以忽略, 这是因为反应物B在上游因化学反应被大量消耗, 到下游时基本消耗殆尽。因此图12中T/NTI层附近对反应物B的输运作用与图11和图13中的反应物A和生成物R相比较小。反应物B的浓度在T/NTI层内主要由对流作用影响, 在T/NTI层内缘附近和湍流核心区主要由对流作用和化学反应共同影响。而在T/NTI层无旋边界附近, 反应物B的标量输运方程中各项皆为0, 这是因为TNTI附近的流动阻碍反应物B向无旋边界输运[28,29]且反应物B在靠近无旋边界之前因化学反应被消耗。

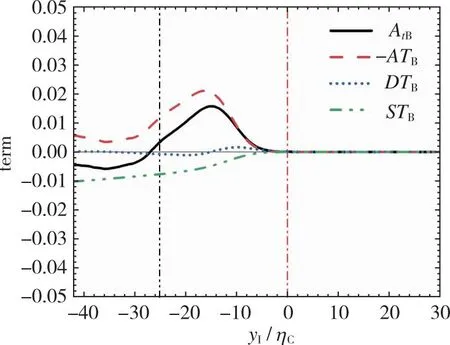
(a) Upstream x/d=10

(b) Downstream x/d=20图12 反应物B的标量输运方程中各项在x/d=10和20的条件平均统计Fig. 12 Conditional average of the terms in the scalar transport equation for the reactant B at x/d=10 and 20

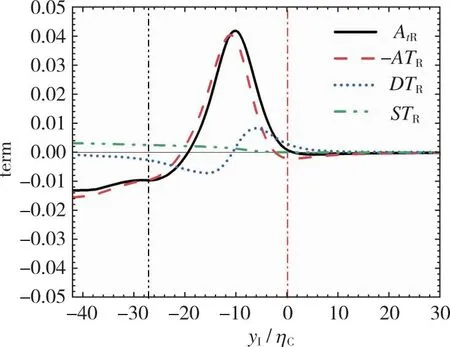
图13为生成物R的标量输运方程中各项在x/d=10和20处的条件平均统计。在无旋边界附近, 生成物R的化学反应源项STR基本可忽略, 其扩散项DTR为产生项, 对流项-ATR为消耗项。此时在x/d=10处,ATR>DTR, 非稳态项AtR<0且数值非常小; 而在x/d=20处, 非稳态项AtR的数值基本为0。因此生成物R在无旋区域和T/NTI层内部之间的输运由对流和扩散作用共同影响, 但生成物R的浓度几乎不随时间发生变化。在x/d=10处的-19

(a) Upstream x/d=10

(b) Downstream x/d=20图13 生成物R的标量输运方程中各项在x/d=10和20的条件平均统计Fig. 13 Conditional average of the terms in the scalar transport equation for the resultant R at x/d=10 and 20

化学反应对组分浓度的影响在x/d=10处比x/d=20处更强烈, 化学反应源项在T/NTI层附近不断消耗反应物A和B, 产生生成物R。随着从无旋区域到T/NTI层, 再到湍流核心区, 化学反应源项条件平均统计的绝对值呈逐渐增加的趋势。统计结果显示上游区域(x/d=10)的化学反应显著发生在T/NTI层内及其附近, 这表明在上游区域T/NTI层内及其附近存在着显著化学反应且随着流向逐渐减弱。与此同时, 下游处T/NTI层附近的化学反应主要发生在远离T/NTI层的湍流核心区。

在无旋边界附近, 反应物A和生成物R的输运主要受扩散项和对流项影响。这是因为流体对组分的输运不仅与扩散作用有关, 还与流体本身的运动状况有关。但x/d=20处T/NTI附近的流动速度较小, 反应物A和生成物R的输运受到射流扩散作用的影响更加显著。相比之下, T/NTI附近的流体在单射流的上游区域具有较高的速度, 因此在x/d=10处射流的对流作用对输运的影响更加显著。

从无旋界面到T/NTI层内缘, 非稳态项的数值先逐渐增大后逐渐减小。其中, 对流项对各组分浓度的影响近似先逐渐增大再逐渐减小; 扩散项对各组分浓度的影响经过两次先增加再减小后趋于0, 这与图10中T/NTI层内各组分浓度梯度先逐渐增大后逐渐减小一致。此外, 在无旋边界处各组分非稳态项的条件平均统计值基本为0, 这表明无旋边界处各组分浓度基本不随时间发生变化。

3 结论

本文利用OpenFOAM中的laminar模型, 针对ΓA0/ΓB0=1时发生二级非平衡基元反应的平面反应性射流, 对T/NTI层附近因化学反应和标量输运导致的各组分产生、 消耗、 输运和混合进行了分析研究, 结论如下:

1) 在整个流场中, 各组分的瞬时非稳态项Atα和瞬时对流项ATα的数值之间几乎呈对称分布, 扩散项DTα和化学反应源项STα数值较小, 对流项ATα在湍流区域对标量输运的影响占主导地位。

2) 流场中的化学反应在上游处较为剧烈且沿着流向逐渐减弱, 在上游区域T/NTI层内及其附近均存在显著的化学反应, 而下游主要发生在远离T/NTI层的湍流核心区。

3) 反应物A和生成物R的输运机制在T/NTI层附近呈现出类似但相反的趋势, 在T/NTI层的无旋边界附近, 反应物A和生成物R的输运主要由扩散和对流作用共同影响, 其中对流作用在上游时产生的影响更大, 扩散作用在下游的影响更大, 但它们的浓度在无旋边界附近基本不随时间发生变化, 而在T/NTI层内和湍流核心区域它们的输运主要受对流作用影响。在T/NTI层内反应物B的输运主要受对流作用影响, 且TNTI附近的流动阻碍化学反应后所余较少的反应物B向无旋边界输运。