基于GPU加速的投影后变分壳模型计算

2024-02-20连占江高早春

原子能科学技术 2024年2期

陆晓,连占江,高早春

(中国原子能科学研究院核物理研究所,北京 102413)

理论上,原子核多体波函数可通过求解薛定谔方程获得。传统壳模型就是在此基础上建立的。然而,由于模型空间的限制,传统壳模型计算仅限于质量数较轻或幻数附近的原子核。对于变形重核,需更大的价核子空间,相应的壳模型组态空间维度数会变得极其巨大,因而无法实现精确的壳模型计算。这是核多体问题中一直存在的难题,且在可见的未来难以被彻底解决。为回避巨大组态空间这一困难,人们发展了各种壳模型近似方法[1-13],以期进一步扩展壳模型应用核区范围。

投影后变分(VAP)方法就是一类较重要的壳模型近似方法[8-13]。它将原子核试探波函数进行变分,从而得到尽可能好的壳模型近似结果。通常情况下,VAP波函数可由投影Hartree-Fock-Bogoliubov(HFB)真空态或投影Hartree-Fock(HF)斯莱特行列式(SD)构成。其中采用HFB真空态完全投影得到具有好量子数(中子数、质子数、角动量和宇称)的波函数需要五重积分,计算非常耗时。而文献[8]的研究表明,在这几种投影中,角动量投影是最重要的。于是,在实际应用中,通常采用HF SD只进行角动量与宇称投影构建初始试探波函数。显然,在相同数目的投影态下,用投影SD作为VAP波函数的近似不如投影HFB真空态得到的结果好。但前者的近似性可通过添加更多的投影SD来改善。在某种意义上,采用投影SD进行投影后变分计算可减少计算消耗。因此,本文采用的VAP波函数全部基于投影SD构建。

然而,随着VAP计算往中重核区推进,计算所需模型空间不断扩大,价核子数目不断增加,为保证计算的精度,就需更多的投影SD参与构建试探VAP波函数,这无疑会造成VAP计算负担的加重,甚至导致VAP迭代收敛非常缓慢。随着半导体和芯片技术的迅猛发展,可提供应用的高性能计算平台不断增加。特别是近年来计算性能飞速提升的图形处理器(graphics processing unit, GPU),其在人工智能、大数据等领域应用广泛,已逐渐取代早期用于并行计算的CPU处理器,成为现代高性能计算的首选。因此,在原子核物理领域,GPU卓越的计算性能也有望进一步提升相关物理模型的计算效率。作为一个具体实例,本文拟将VAP壳模型计算程序从传统的CPU平台移植到GPU平台,以期进一步提升VAP的计算速度。

本文将从VAP的原理出发,介绍其在计算当中遇到的数值问题,基于OpenACC并行化模型实现VAP在GPU平台上的计算,并通过实例展示采用GPU相对于CPU在计算效率上的提升。

1 VAP的数值问题

首先,采用投影SD构建的试探VAP波函数可写为如下形式[12]:

(1)

(2)

(3)

DVAP=N(MN-N)+Z(MZ-Z)

(4)

在VAP计算中,将变分参数取为复数的形式。于是,采用n个SD构建的VAP波函数,其独立变分参数就有2nDVAP个。可见,随着模型空间的增大、价核子数目的增多以及SD数目的增加,将会导致独立变分参数迅速增加。

(5)

在最小化能量之和的过程中,为保证VAP计算的稳定性,在迭代过程中计算能量的梯度与Hessian矩阵[9]。即计算了如下4类矩阵元:

(6)

(7)

此外,在VAP计算中,哈密顿量通常取为如下形式:

(8)

其中:tij和vijkl分别为单体和两体相互作用矩阵元;c+和c分别为粒子产生和湮灭算符;i、j、k、l分别表示不同的单粒子轨道。由式(8)可看出,在两体相互作用下,单个投影矩阵元在特定积分格点处的分量通常包含一个对单粒子轨道的4重求和。

基于以上讨论可看到,在VAP计算中,投影矩阵元的计算占据了大部分计算时间。并随着模型空间的增大,价核子数的增多,计算时间会迅速增加。为更直观体现这种计算耗时,以sd模型空间的24Mg与pf模型空间的56Ni的基态为例,采用1个SD,即n=1,对24Mg基态到56Ni基态投影矩阵元计算量的增加做一定量估计。首先,对24Mg的基态,每个方向上只需选取8个格点就足以得到好的积分结果。而计算56Ni的基态,每个方向上积分格点的数目通常需增加至18个。因此,从24Mg到56Ni,总的积分格点数目增加约了10倍。因为做简单估算,将单个投影矩阵元在特定积分格点处每重求和的求和次数取为原子核所在模型空间的中子轨道数的一半。此时,24Mg所处的sd壳包含12条中子轨道,对应的总求和次数为1 296,而56Ni所处的pf模型空间则包含20条中子轨道,其总求和次数为10 000,接近24Mg求和次数的8倍。最后24Mg共有64个独立的变分参数,对应有64个梯度分量和2 080个独立的Hessian矩阵元,56Ni则共有192个独立的变分参数,对应有192个梯度分量和18 528个独立的Hessian矩阵元,分别是24Mg数目的3倍和8.9倍。因此,从24Mg的基态到56Ni的基态,总计算量增加了近780倍,且这一数字随着模型空间的增大和价核子数目的增加会进一步增大。所以,如果采用传统的串行VAP计算,在时间上是不可接受的。

在VAP中,式(6)所示的投影矩阵元之间是相互独立的。因此,为节省计算时间,实际的VAP计算一般需借助并行技术实现不同独立格点的同时计算。在之前的工作中,为提高中重核区的VAP计算效率,主要通过OpenMP等并行方法将不同积分格点处的转动矩阵元计算任务分配给不同的CPU核心执行,从而实现对不同积分格点处转动矩阵元的同时计算。在这种模式下,同一积分格点处的不同转动矩阵元仍以串行方式逐个计算。从上面的讨论可知,同一积分格点处存在大量相互独立的转动矩阵元。显然,这些独立的转动矩阵元也可采用并行方式同时计算。因此,一种更有效的加速方式是将所有独立的转动矩阵元同时并行化。当然,这也意味着需更多的计算核心。在这方面,内嵌数千个CUDA内核的高性能GPU无疑较一般只有几十或上百个核心的CPU计算服务器具更大优势。因此,为进一步提升VAP的计算效率,有必要将当前的程序代码移植到GPU平台上进行加速计算。

2 基于OpenACC的GPU加速VAP程序改造

GPU是一种多核协处理器,通过PCIe总线与CPU相连。在并行计算中,程序总是从CPU开始执行,由CPU负责执行串行代码并为并行计算做好准备,包括数据初始化、分配GPU内存、将数据复制到GPU等。当程序运行到计算密集区域时,CPU以特殊形式调用GPU,由GPU完成并行计算并将结果返回到CPU继续向下执行。本文选用的GPU加速器为英伟达公司生产的Tesla V100。1块Tesla V100 GPU共有5 120个CUDA内核和640个Tensor内核,不仅为Tesla V100提供了多核并行计算的结构基础,也使其具备更高的浮点运算能力。目前,Tesla V100单精度浮点运算每秒峰值速度可达到15.7TFLOPS。

OpenACC是一基于指令的高级编程模型。编程人员只要在串行的C/C++或Fortran程序中插入合适的指令,支持OpenACC的编译器就会根据指令的内容产生可执行的低级语言代码,将指令指定范围内的计算密集的代码分派给GPU等加速器并行完成。对于不支持OpenACC的编译器,指令会被当成注释自动忽略。这种机制不仅有效地减少了对原程序的改动,也有利于程序的跨平台运行。

基于OpenACC并行化模型可对VAP程序进行改造,将其移植到GPU平台进行加速。由于VAP计算中的投影矩阵元之间是相互独立的,因此,在将程序移植到GPU平台的过程中,基本的思路就是利用OpenACC并行方法将同一积分格点处所有独立的转动矩阵元算出,然后对不同积分格点处的转动矩阵元求和得到相应的投影矩阵元。

经GPU移植后的程序执行流程如图1所示,图中蓝色程序块表示串行区域,由CPU执行,橙色程序块表示并行区域,由GPU执行。在程序执行过程中,首先由CPU完成初始化和预处理,再将初始基矢波函数和两体相互作用信息从CPU内存拷贝到GPU内存开启投影矩阵元的并行计算。待并行计算结束后,再将计算结果从GPU内存拷贝到CPU内存,在CPU上求解波函数满足的HW方程,从而得到能量及其相应的梯度和Hessian矩阵,利用信赖域算法得到下一次迭代的初始波函数。重复以上过程直至能量达到极小。

图1 OpenACC版本VAP程序流程图

3 GPU加速效果检验

计算中选用的计算平台为DELL PowerEdge T640服务器,每台服务器同时搭载2颗Intel(R) Xeon(R) Gold 6148 CPU(20核|2.40 GHz) 和1颗英伟达公司生产的Tesla V100 GPU。

为检验经GPU移植后的VAP程序的正确性,从同一SD出发,分别用原来经过检验的OpenMP并行程序和新的OpenACC并行程序在sd壳对24MgJπ=0+、2+、4+、6+的低自旋态开展了完整的VAP计算。计算中所用的哈密顿量为USDB有效相互作用[16]。图2给出了两种情况下VAP能量随迭代步数的变化。对于计算的所有自旋态,OpenACC并行程序每步得到的VAP能量与OpenMP并行程序得到的结果在计算机误差范围内完全一致。变分达到收敛所需要的迭代步数也完全相同。这证明经GPU移植后得到的OpenACC并行程序的正确性。

为进一步对比原来OpenMP并行程序和新的OpenACC并行程序的加速效果,分别计算VAP程序在CPU串行(单核)、CPU并行(40 核)和GPU并行3种条件下的单步运算时间。计算中只用1个SD,并固定迭代步数为10步。单步运算时间定义为每次VAP迭代中计算式(6)的所有投影矩阵元平均需要花费的时间。并行单步运算时间与串行单步运算时间的比值称为加速倍数。

图3给出了OpenMP并行程序和OpenACC并行程序在计算部分sd壳原子核基态时的加速倍数。从图3可看出,经并行后,VAP程序的运算速度相比串行模式下有了较大的提升,且GPU并行的加速效果显著优于CPU并行。对于28Si,GPU并行的加速倍数达到了接近50倍,而CPU并行的加速倍数只有不到11倍。此外,无论是采用CPU并行还是GPU并行,其加速倍数均随价粒子数的增多而增大。不同的是,GPU并行的加速倍数的增长速度明显高于CPU并行。从23Na到28Si,GPU并行的加速倍数增大了1.2倍,而CPU并行的加速倍数只增长了53%左右。这主要是因为sd壳模型空间较小,并不足以让GPU核心得到充分利用。这一点也直接体现在VAP程序执行过程中的GPU核心占用率上。如在计算23Na时,GPU核心的占用率约60%,这意味着仅60%的GPU核心得到了利用。而在计算28Si时,这一数字达90%。因此可预见,随着模型空间的增大和价粒子数目的增加,GPU并行的加速效果仍有望得到进一步提升,直至核心占用率达到100%。

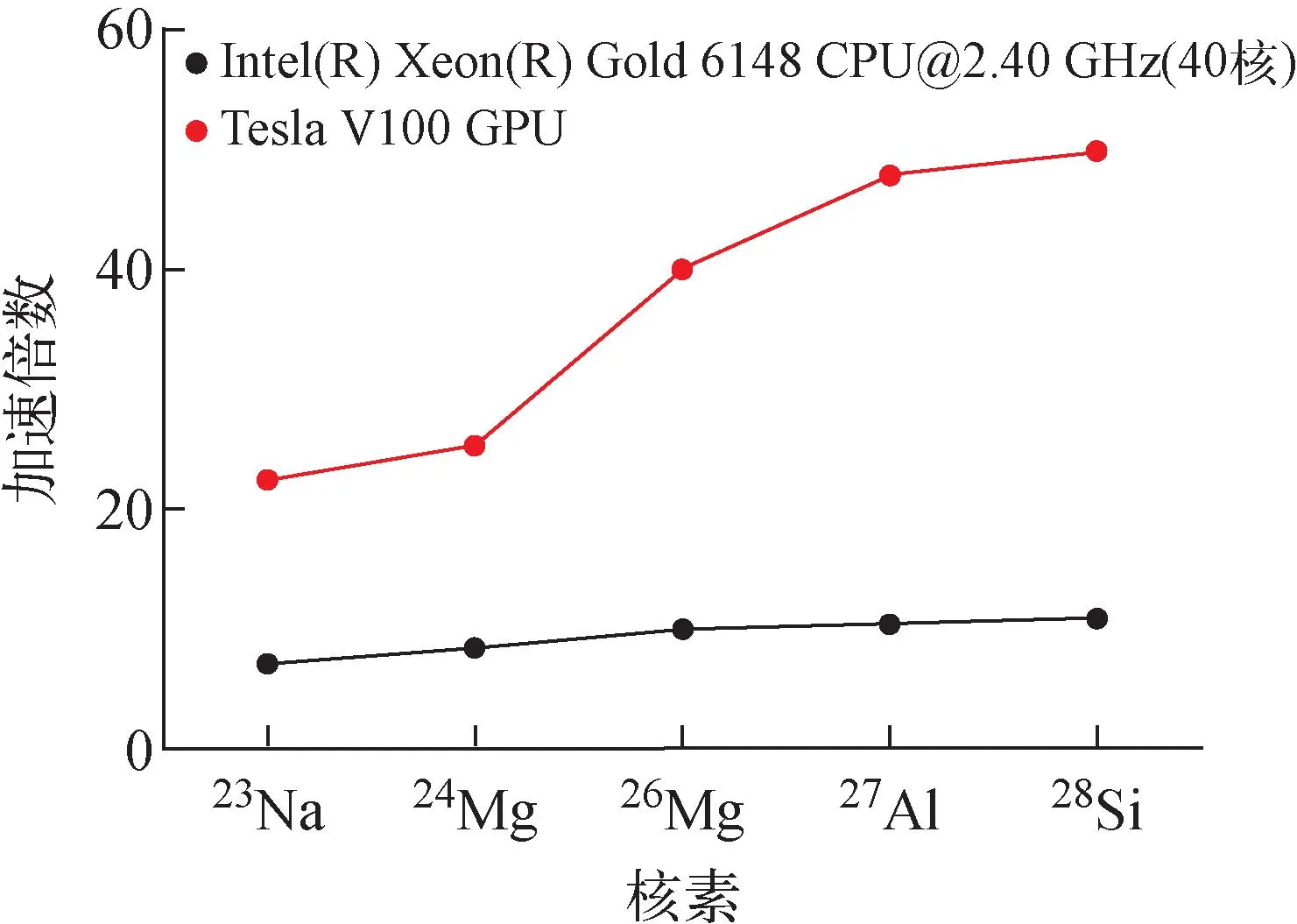
图3 CPU并行与GPU并行加速倍数随不同原子核的变化

为进一步测试GPU并行的加速效果和验证经GPU加速后的VAP程序在中重核区的适用性,在相同的平台下对64Ge的基态开展了完整的VAP计算。采用fpg9/2模型空间,fpg9/2模型空间包含30条中子轨道和30条质子轨道。在此模型空间中,64Ge的组态空间维度达1.7×1014,较组态相互作用壳模型目前能解决的范围高出3个数量级。在本次计算中仍然采用1个SD。在此情况下,GPU核心占用率达到了100%,加速倍数更是高达192倍。与CPU并行(40核)相比,单步运算时间从原来的75 min降到了9 min。

最后,作为一大规模壳模型计算应用实例,利用OpenACC并行程序对稀土区重核178Hf的基带开展了计算。178Hf所处的jj56pn模型空间包含32条质子轨道和44条中子轨道。在此模型空间中,178Hf的组态空间维度达到了1.9×1018,较传统的严格对角化方法的处理极限高7个数量级。处理如此大维度的计算问题,原来的OpenMP程序迭代1次需花费超过1 d的时间,而经过GPU加速的OpenACC并行程序迭代1次只需1.5 h左右。

图4给出了采用一个SD进行VAP计算得到的178Hf基带能谱。计算采用的相互作用为jj56pnb有效相互作用[17],实验数据取自文献[18]。从图4可看出,通过VAP计算得到的178Hf基带能谱与实验值符合得很好,对应能级之间的能量差最大不超过400 keV。

图4 178Hf基带能谱

4 总结与展望

VAP方法作为一种重要的壳模型近似方法,有望在较大模型空间中实现对中重核区原子核的计算。但在向中重核区推进的过程中,随着模型空间的增大以及价核子数的增多,VAP需计算的投影矩阵元的数目会迅速增加,极其耗费计算时间。由于投影矩阵元之间彼此是相互独立的,因此,VAP计算可通过并行化处理以提高计算效率。随着近年来高性能GPU计算平台的迅速发展,相较于原来在CPU平台上采用OpenMP并行化程序进行VAP计算,在高性能GPU平台上采用OpenACC并行化模型进行计算有望进一步提升计算效率。通过将VAP程序采用OpenACC并行化模型改造,在角动量投影的每个积分格点上,实现了数目庞大的各独立转动矩阵元的GPU并行化计算。经验证,GPU加速后的VAP程序与原来的OpenMP并行化程序相比,计算效率进一步提升了数倍。且随着往重核区的推进,提升倍数会进一步增加。采用改造后的程序,首次实现了稀土区重核178Hf的基带能谱的计算。目前,VAP程序只是在1块GPU内进行了加速,其计算效率即得到显著提升。可预见,若采用多块GPU同时对VAP程序进行加速,将会进一步提升VAP的计算效率,使得VAP计算更易往重核区推进。这一工作将会在未来展开。

GPU加速的VAP计算程序首次具备了在GPU服务器单机开展重核区计算的能力,不仅节省了大量的能耗,同时为系统研究中重质量核区复杂原子核结构问题提供了极大的便利。过去,重质量原子核的大规模壳模型计算即使在超级计算机集群上也难以开展起来,对重质量原子核结构的系统研究普遍缺乏微观的壳模型基础。目前对于许多复杂核结构现象的理解还处于比较模糊的认识阶段,如γ振动带与β振动带的同时描述,复杂的奇A核与奇奇核八极转动带,超形变带的带间跃迁等。对这些现象的深入理解必须借助于可靠的微观壳模型方法。本文建立的VAP壳模型计算将有望在这些问题上发挥其独特作用。