基于汉宁窗变密度条纹的储罐沉降视觉测量方法

伏喜斌，魏 崴，黄学斌，刘东明，钟剑锋，王 东，钟舜聪，张 焱

（1.厦门市特种设备检验检测院，福建 厦门 361000；2.福州大学 机械工程及自动化学院，福建 福州 350116；3.中国航空油料有限责任公司厦门分公司，福建 厦门 361000；4.浙江创力电子股份有限公司，浙江 温州 325025）

引言

随着我国石油、化工等工业的发展，储罐在国内得到了广泛的应用，并且朝着大型化、集群化方向快速发展。受场地稳定性、不良地质体、地表水下渗等影响，储罐地基常会发生沉降，威胁其安全运行，如造成储罐局部应力过大及罐壁的椭圆化等，从而引发破裂、漏油等灾难性事故。储罐作为石化行业重要的存储设备，其安全问题不容忽视。因此对储罐的沉降测量方法研究受到越来越多学者的关注。

传统沉降测量方法主要采用水准仪和全站仪的水准测量法和三角高程测量法，该类方法比较费时费力、难以实现全天候实时监测和预警等。目前常用的沉降自动监测设备主要有GPS、合成孔径雷达、激光测量系统、静力水准仪、光学成像系统和视觉测量系统等。

许多研究者采用北斗卫星导航定位系统实现桥梁、矿区、高铁、机场、高压输电塔塔架等的沉降测量[1-2]，测量精度可达1 mm～2 mm。YANG Zefa[3]等对合成孔径雷达干涉测量技术进行研究，并应用于地面沉降的监测。当前合成孔径雷达干涉测量技术测量精度也在毫米量级。由于光纤式传感器具有不带电、不受电磁干扰、稳定可靠等优点，也有研究学者提出了各类光纤传感器用于结构的沉降监测[4]。孙丽[5]等设计出一种等强度梁的新型双光纤光栅静力水准仪，提出了一套沉降监测系统方案，并进行了沉降监测试验。XU Dongsheng等[6]提出一种自动温度补偿的光纤式液位传感器用于结构的沉降监测，测量范围为±75.61 mm，测量相对误差为4%。王来志[7]等分析了现有的沉降检测技术的优缺点，结合现场实际施工情况，设计了一套基于压差式静力水准仪的沉降监测物联网系统。

随着视觉传感器和图像处理技术的发展，许多研究学者也提出各种基于视觉图像的位移、形变等测量方法和系统[8-10]，并在结构状态监测与缺陷检测中得到一定的应用。视觉测量一般在被测结构表面设置由规则特征图案或者散斑图案组成的标靶，再采用图像对比跟踪算法[11]、模板匹配技术[12]、边缘检测技术[13]、数字图像相关算法[14]等进行动态信号的分析提取，该类视觉测量系统的测量性能取决于算法的精度和图像的分辨率，通常可实现亚像素级别的图像位移的分辨，但是算法计算量较大。也有学者采用机器视觉，结合目标匹配和方向码匹配算法捕捉结构自然特征的运动实现结构的位移测量[15],取得一定的效果，但位移分辨率受光照条件及图像质量的影响较大。

现有的储罐沉降监测系统较为复杂，测量精度有限，且容易受到外部环境干扰因素的影响导致测量可靠性不高。为了更加简便快速解决对储罐沉降测量问题，提升测量的便捷性，提高结构沉降的测量精度和可靠性，本研究提出一种汉宁窗变密度条纹作为标靶附于被测结构表面，采用二维远焦视觉成像系统采集标靶图像方式对储罐的沉降进行测量，处理算法简单高效，且具有微米量级的沉降位移测量精度。因此，提出的测量系统组成简单，测量方便，精度较高，能够很好地克服现有测量方法存在的系统复杂、测量精度不足等问题。

1 测量系统组成

基于汉宁窗变密度条纹和远焦相机的储罐沉降测量系统示意图如图1 所示。该测量系统主要由附于储罐表面的汉宁窗变密度条纹、远焦相机和计算机组成。该测量系统的三维测量坐标定义如图1 所示，将垂直于成像光轴的水平方向定义为X轴，垂直于成像光轴的竖直方向定义为Y轴，沿成像光轴方向定义为Z轴。

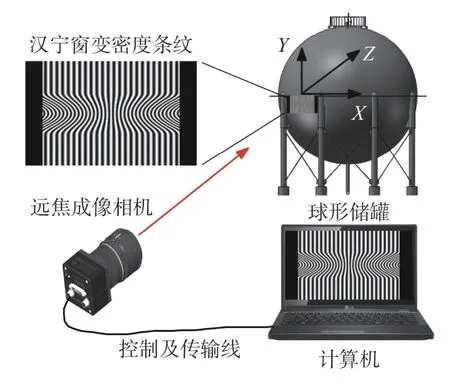
图1 储罐沉降测量系统示意图Fig.1 Schematic of tank settlement measurement system

汉宁窗变密度条纹形式如图1 所示，该条纹通过程序产生，再将其保存成黑白图片。实际测量中可将该图片喷涂于被监测储罐的表面，或者打印于特殊背胶贴上，粘贴于被测结构表面。实际汉宁窗变密度条纹的有效条纹高度和宽度分别假设为H和W，其值可由实际成像距离决定。该条纹的特点在于沿高度方向的条纹密度随汉宁窗函数变化，采集到条纹图像后，通过计算每行条纹的密度值即可得到汉宁窗变化的密度曲线，再通过求取该密度曲线的能量重心坐标，即可得到条纹在竖直方向的位移变化信息。在被测结构表面布置好条纹后，尽量使条纹图像成像于图像传感器的中心位置，并调整远焦成像镜头的参数使条纹清晰成像。因为该类大型结构的沉降速度一般较慢，所以采用高分辨率、低帧率的普通相机即可。

2 测量原理

2.1 Y 方向沉降位移测量原理

系统Y方向的沉降位移测量原理如图2 所示。附于储罐结构表面的条纹图像将跟随储罐一同沉降，所以成像条纹图像在成像传感器竖直方向的成像位置将发生变化，通过定位条纹中心在竖直方向偏移的像素值h即可计算得到储罐沉降的实际位移。由图2 中成像关系可得，结构在t时刻沿Y方向有位移 Δy(t)时，其位移可表达为

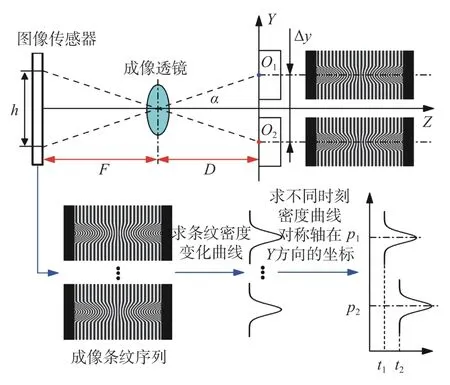
图2 Y 方向沉降位移测量原理Fig.2 Measurement principle of tank settlement displacement in Y-direction

式中：D为成像物距；F为图像传感器和透镜之间的成像距离；h(t)为汉宁窗变密度条纹高度方向的对称中心线在图像传感器上相对于参考条纹中心线的偏移量，该偏移量可由式h(t)=aΔm(t)计算获得，其中a为图像传感器的像素点宽度，Δm(t)为t时刻成像条纹中心线在图像传感器上相对于参考条纹中心线偏移的像素点数；M为位移比例系数。所以通过式（1）即可求得储罐的实际沉降位移。

在实际测量中，相机的成像距离和成像物距在调整焦距过程中会发生变化，因此该参数不容易准确获得。为此需要设计一种方法来确定位移比例系数M，该系数的确定方法如下：1）将成像相机的位置调整好，假设为位置1，再调整成像镜头的成像参数，使条纹清晰成像于成像传感器中；2）在该位置下拍摄多张条纹图像，求取每张条纹图中心位置，再取多张条纹对称中心坐标的平均值作为参考坐标；3）使相机在Y方向移动一个已知位移 Δy到位置2，在位置2 拍摄多张条纹图像，求取每张条纹图中心位置，再取多张条纹对称中心坐标的平均值作为位置2 下条纹对称中心坐标；4）求位置2 和位置1 平均对称中心坐标的绝对偏移像素值 Δm，再计算 Δy和 Δm的比值即可确定位移比例系数M。因此，在设计相机安装架时，可在其竖直方向配置一个微型移动平台，用于产生确定的Y方向位移，以便于位移比例系数M的确定。

2.2 汉宁窗条纹对称中心的确定

由Y方向的沉降位移测量原理可知，精确得到储罐沉降位移的关键在于精确定位成像条纹在高度方向的中心位置。所设计条纹图像特点在于条纹密度在高度方向上成汉宁窗函数变化，因此只要求出该密度变化曲线，即可通过能量重心校正法求得条纹的对称中心坐标。要求出条纹高度方向的条纹密度变化曲线，可通过每行条纹的频率变化求得，而条纹的频率则可通过对每行条纹的傅里叶变换获得，但是采用傅里叶变换计算条纹的频率时会因频谱泄漏而产生误差。为了获得更为精确的条纹频率信息，在对每行条纹频率进行计算时采用能量重心校正法[16]进行校正，可得到更为准确的条纹频率变化曲线，即条纹密度变化曲线，如图2 所示。

在原理上，直接将汉宁窗变化曲线代替条纹图附于储罐结构表面，再从图像中提取曲线轮廓进行对称中心的计算也是可行的。但是实际测量中光线的变化，可能影响曲线的清晰成像，从而影响轮廓提取。更为重要的是，因为相机像素点分辨率的限制，得到的汉宁窗曲线轮廓并非是连续变化的光滑曲线，而在求取汉宁窗函数曲线的能量重心时，其各点的幅值对于对称中心坐标计算精度影响较大，在采用能量重心校正法计算其对称中心时产生的误差比较大。本文提出通过求取条纹密度变化获得汉宁窗变密度曲线的思路主要是为了获得精确和连续变化的汉宁窗密度变化曲线，因为通过整体条纹来求密度变化，外部光照的变化导致的条纹强度变化对频率的影响较小，而且通过频率的能量重心校正可获得超像素分辨的汉宁窗密度变化曲线，进而得到更为准确的对称中心坐标，提高沉降位移的测量精度。

3 系统测量性能影响因素分析

由储罐沉降测量原理可知，本方法通过图像采集处理的方法实现储罐沉降位移的测量。为了对测量系统相关影响因素进行分析，采用SOLIDWORKS 软件建立储罐模型，采用软件的运动仿真模块模拟储罐的沉降，在沉降运动中采用软件的成像模块进行汉宁窗变密度条纹图像的连续采集。因此在仿真模型中可以对多个影响因素进行仿真设置，从而研究其对测量性能的影响。

当前的图像打印精度较高，可以较好地保证条纹图像的打印质量。然而在实际的成像过程中，条纹图像的环境光照质量、成像镜头的参数、成像相机的成像参数（如像素分辨率、像素位深、成像噪声等）等对条纹的成像质量都会产生一定的影响。对于环境光照，如果要实现储罐全天候的监测，则需要配置相应的照明光源，保证条纹图像的光照质量。

为了研究成像条纹信噪比对测量精度的影响，采用仿真模型模拟了结构在1 s 内沉降0.1 mm 的情况，并用20 frame/s 的采样帧率对沉降过程中的条纹图像进行连续采集，条纹图像的分辨率为1 920×1 920 像素，像素位深为8 位。然后对采集的条纹序列分别加入不同分贝的高斯白噪声，得到7 组噪声分别为0 dB、10 dB、20 dB、30 dB、40 dB、50 dB 和60 dB 的条纹序列，其中0 dB、20 dB、40 dB和60 dB 的条纹信号如图3(a)所示。再采用提出的条纹图像处理和位移提取算法得到不同噪声下的位移曲线，如图3(b)所示。

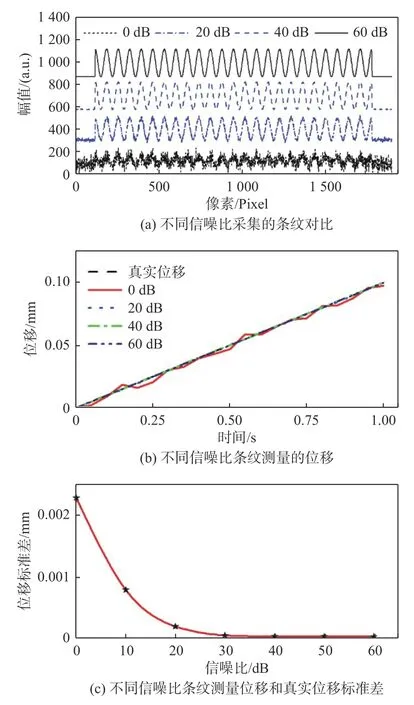
图3 不同成像条纹信噪比与测量性能关系Fig.3 Relationship between SNR of different imaging fringes and measurement performance

在条纹图像的信噪比为0 dB 时，得到的位移曲线存在一定的噪声，主要在于噪声太大时得到的密度变化曲线噪声较大，在计算汉宁窗曲线对称中心时会引入一定误差。但在密度曲线的噪声大于20 dB 时，通过平滑方法可得到光滑的密度变化曲线，从而得到较准确的对称中心坐标，因此测量位移曲线可以和真实位移曲线高度重合。不同信噪比下测量的位移和真实位移之间的标准差如图3(c)所示。所以在实际测量中要尽量得到信噪比高的条纹图像，使测量性能得到保证。

条纹图像的光照质量对成像质量有一定的影响。因此在图像分辨率为1 920×1 920 像素、像素位深为8 位、图像信噪比为40 dB 条件下，模拟环境光照系数分别为0.2、0.4、0.6、0.8 和1.0 条件下对1 mm 的沉降位移进行测量，不同光照条件下条纹的强度变化如图4(a)所示，可知环境光照不同会影响成像条纹的对比度。不同光照条件下测量得到的位移如图4(b)所示，其与实际位移之间的标准差如图4(c)所示。由结果可知，不同光照条件下都可以较精确地测量得到结构的沉降位移。虽然环境光照条件会改变条纹的成像对比度，但是本文提出的方法主要基于条纹的密度变化信息，只要保证成像的条纹对比度足够用于计算条纹的频率信息即可满足测量基本条件，所以本方案具有较好的测量适应性和稳定性。

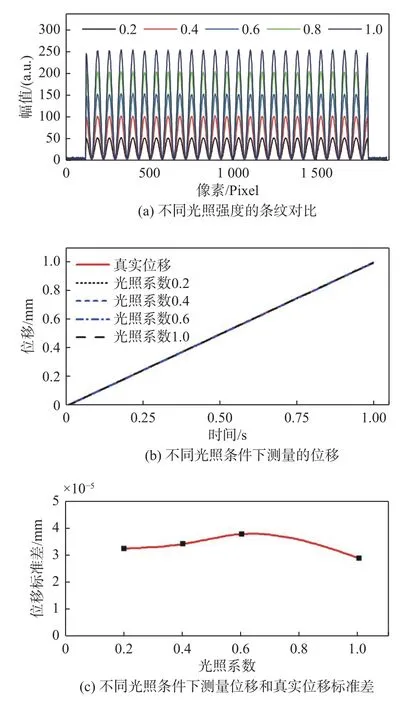
图4 不同光照条件对测量的影响Fig.4 Influence of different illumination conditions on measurement

为了探讨成像分辨率对测量性能的影响，设定结构的线性沉降位移为1 mm，通过改变成像参数，得到条纹成像分辨率分别为128×128 pixel、256×256 pixel、512×512 pixel、768×768 pixel、1 024×1 024 pixel 的5 组条纹图像序列，每组条纹图像的条纹信噪比都为40 dB，对每组条纹进行位移的求取，得到的位移曲线如图5 所示。因为本汉宁窗变密度条纹的条纹周期变化范围为24～36 周期，根据采样定律，在水平方向上的条纹采样点数应该大于90 个采样点即可满足条纹的采样，从而实现条纹密度的求取。但是在实际测量中因存在噪声、光源波动等因素影响，应该在条件允许情况下尽量使更多的像素点用于条纹的采样，从而提高条纹密度信息提取的精度。

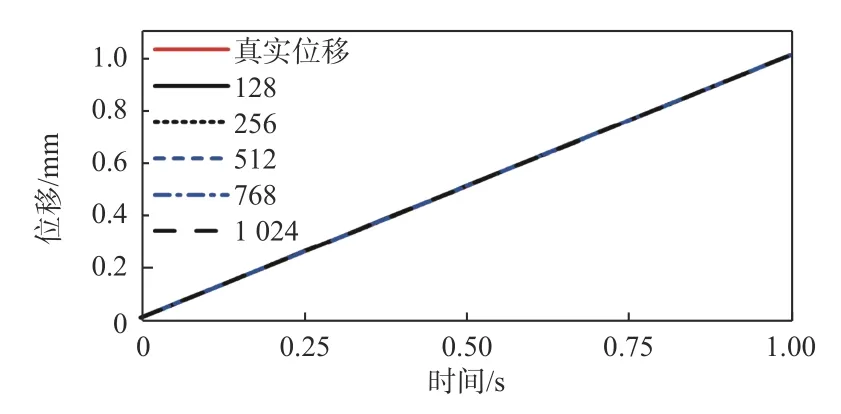
图5 不同成像分辨率对测量的影响Fig.5 Influence of different imaging resolution conditions on measurement

4 实验及分析

为了验证提出的测量系统对储罐下沉测量的可行性与准确性。采用一维电动移动平台(THORLAB：MTS25/M-Z8)产生已知位移来进行验证。实验装置如图6 所示。将一维移动平台在竖直方向安装，将高度和宽度分别为7 cm 和14 cm 的汉宁窗变密度条纹图像粘贴在轻质塑料平板表面，再将塑料板安装于移动平台的移动台上。移动平台的位移大小和移动方式可通过计算机中的MATLAB 软件进行控制。

图6 实验装置图Fig.6 Physical drawing of experiment setup

实验中采用分辨率为4 096×3 000 像素的成像相机（Point Gray，最大帧率30 frame/s）对条纹图像进行采集，采用远焦镜头（JARAY，焦距420 mm～800 mm F8.3）进行成像。实验前，将条纹成像相机放置于距离成像条纹7.5 m 处，放置好成像相机使汉宁窗变密度条纹成像于图像传感器内，调整好成像镜头和图像传感器的各参数使条纹图像清晰。为了减小单张图片的大小，本实验中没有使用相机的全像素进行成像，实际条纹在成像传感器中的采样分辨率为950×2 400 像素，曝光时间为5 ms，采样帧率设置为20 frame/s。

设置好条纹和沉降测量系统后，对一维电动移动平台施加一维连续运动，因为移动平台使用滚珠丝杆进行驱动，可以通过设置不同电机旋转加速度和最大速度来模拟不同沉降速度。测量前将移动平台的位移设置到22 mm 行程位置处，然后采集100 张条纹图像，计算每张条纹图中汉宁窗变密度曲线的对称中心在成像传感器中的成像位置，再取其平均值作为该位置条纹中汉宁窗变密度条纹的中心位置。再将移动平台移动到位置2 mm 行程位置处，采集100 张条纹图像，同样取每张条纹图像中汉宁窗变密度条纹对称中心的平均值。然后将已知位移20 mm 除以两个位置的像素坐标绝对值，求出位移比例系数。在实际的测量中是不可以预先让被测结构下沉一定位移的，所以可以在相机安装位置设置一个竖直方向移动平台或升降平台，从而实现确定相对位移的产生。应注意的是，位移比例系数的计算应该是在条纹的安装位置、相机的成像位置及成像参数等都确定好后进行标定，在测量中改变条纹、相机位置参数或者镜头成像参数都应该进行重新标定。

在前面模拟中分析了光照条件不同情况下的测量效果，只要能够对条纹信号进行采集成像，即使在低条纹对比度的情况下也具有较好的测量精度。因此，在晚上或者光照条件较差时只需增加一个稳定的外部光源即可使条纹获得较好的成像对比度，从而保证沉降位移监测效果。而在实际的测量环境中，外部光照条件还会随着太阳光照的改变而变化。为了进行进一步的试验验证，在两种光照条件下对10 mm 的连续位移进行了测量。实验中采用强外置光源来改变条纹的光照条件以模拟强太阳光照情况，正常室内光照条件模拟正常光照情况。两种光照条件下的成像条纹强度曲线如图7(a)和图7(b)所示。可见正常室内光照条件下成像条纹强度信息可正常获取，对比度正常；而强光照条件下会导致条纹反射光过于强烈，从而使成像传感器过曝光，使成像条纹变形。

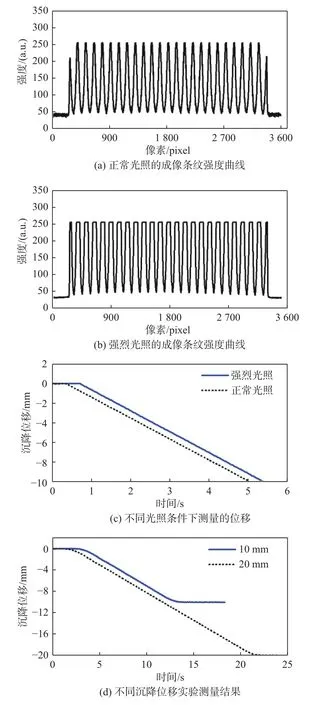
图7 不同光照条件下线性移动平台下降位移测量结果Fig.7 Measurement results of decline displacement for linear mobile platform under different illumination conditions

标定完位移比例系数后，将移动平台加速度和最大速度分别设置为2 mm/s2和2 mm/s，设置移动平台从22 mm 连续下降至2 mm。在前面两种光照条件下对移动平台的沉降位移进行测量。测量结果如图7(c)所示，可见在两种光照条件下皆可准确获得结构的位移信息。因此，提出的条纹图像处理方法对条纹成像质量要求不高，可适用于实际环境光照多变的测量场合。为了对不同速率沉降进行监测，将移动平台加速度和最大速度分别设置为1 mm/s2和0.5 mm/s。分别设置移动平台从22 mm 连续下降至2 mm 和12 mm 位移处，下沉过程中连续采集条纹图像并经处理后得到实际沉降位移曲线如图7(d)所示。由实验结果可知，该测量方法可在远距离测量条件下实现结构的大范围内沉降位移的实时监测。

为了对该实验条件下测量系统的测量位移精度进行分析，使移动电动平台产生间歇下沉位移分别为10 μm、25 μm 和50 μm 的3 种运动，每下沉一次位移后停留1 s。通过该测量系统得到的位移曲线如图8 所示。由图8(a)可知，在阶梯沉降步长为10 μm 时得到的位移曲线存在一定的噪声，但是整体上还能准确分辨出每一个步长之间的位移差。步长为25 μm 和50 μm 的测量结果可以较好地得到与实际的沉降位移一致的下沉曲线。因此该测量系统在该条件下可实现小于10 μm 下沉位移的测量，具有较好的位移测量精度。

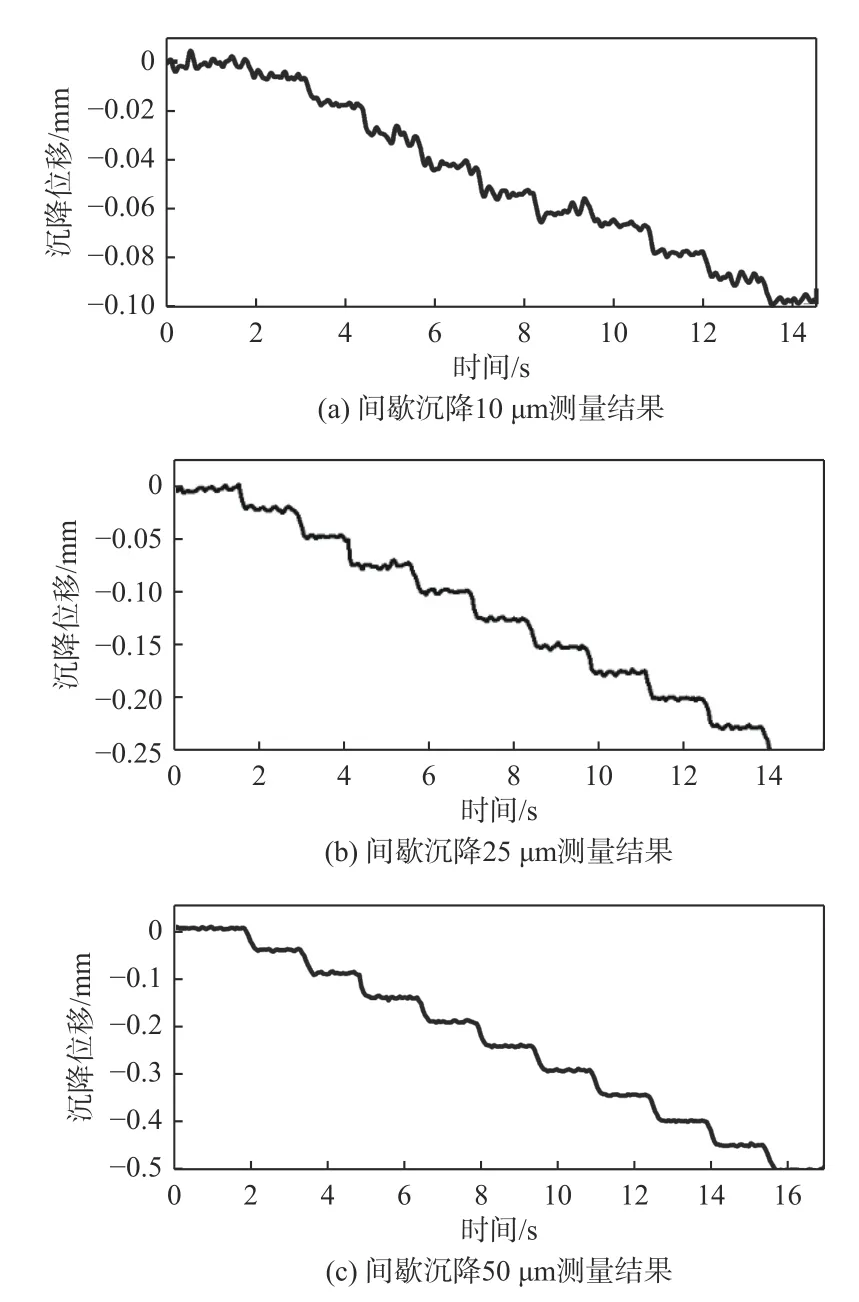
图8 不同间歇沉降位移实验测量结果Fig.8 Experimental measurement results of different intermittent settlement displacements

5 结论

本文提出了一种基于汉宁窗变密度条纹和视觉相机的储罐沉降位移监测新方法，通过软件建模仿真分析了影响该测量系统测量精度的各种影响因素。模拟结果表明，条纹图像的信噪比大于20 dB 以上即可达到较好的测量效果，在满足条纹频率信息准确提取的条件下，增加光照条件，提升条纹的对比度和增加条纹的采样分辨率对测量性能的提升有一定提升，但不显著。实验结果表明，该系统可精确地实现结构大沉降范围内位移的测量，测量距离为7.5 m 条件下沉降位移测量精度可优于10 μm。随着视觉测量技术的发展，各类高性能的成像系统将得到更为广泛的使用，该测量系统组成和测量原理简单，可方便地应用于各类线性位移的测量中，具有一定的推广应用价值。后期将进一步研究该测量方法在结构倾斜测量方面的应用，进一步扩展其测量维度。