自适应光学系统迭代控制算法超参数优化

罗宇湘，杨慧珍，何源烽，张之光

（1.江苏海洋大学 电子工程学院，江苏 连云港 222005；2.金陵科技学院 网络与通信工程学院，江苏 南京 211169）

引言

自适应光学（adaptive optics，AO）技术采用变形镜或空间光调制器校正光波前畸变，改善光学系统性能，已经在天文领域[1]、生物领域[2]、医学领域[3]和半导体领域[4]得到应用。传统自适应光学系统需要独立的波前传感器，系统结构复杂；而以系统性能指标作为目标函数，使用优化算法迭代控制变形镜电压，则能够在无需波前传感器的条件下实现波前畸变校正（也称为无波前探测自适应光学技术）。无波前探测自适应光学系统中，迭代控制算法的超参数选取决定了自适应光学系统的校正能力。例如在随机并行梯度下降（stochastic parallel gradient descent algorithm，SPGD）算法中，超参数选取过小时，会使得系统的收敛速度慢，在结束既定步数的迭代后，未能达到稳定收敛；超参数选取过大时，在迭代开始阶段收敛较快，但算法容易陷入局部极值[5]。自适应光学系统迭代控制算法一般依靠遍历或者经验来确定超参数。近年来，随着机器学习领域中越来越多的优化器被应用于自适应光学系统的迭代控制，采用的优化器包括Momentum[6]、Nesterov accelerated gradient（NAG）[7]、AdaGrad[8]、RMSprop[9]、Adam[10-11]、Nadam 等[12]，迭代控制算法的超参数数目显著增长，通过遍历来确定超参数最优值所需的运算量激增。针对这一问题，本文提出一种基于贝叶斯优化的自适应光学系统迭代控制算法的超参数选取方法，能够以较小的运算量确定超参数的最优值。

超参数搜索可以看作是黑箱函数的优化问题，该函数往往具有非凸特征。采用常规的遍历法搜索超参数可能因为找到一个局部最优值而错过全局最优值。PELIKAN M 等于1998 年提出贝叶斯优化[13]，SNOEK J 等于2012 年将贝叶斯优化调整超参数用于机器学习领域[14]。贝叶斯优化具有迭代次数少、速度快和针对非凸问题依然稳健等优点，在应用于超参数优化实践中，已被证明[14-15]与网格搜索[16]和随机搜索[17]相比，能在更少的评估中获得更好的结果。和传统的遍历法不同，贝叶斯优化是一种能够利用有限的函数采样值，以较少的评估次数获得复杂目标函数最优值的方法[18]。为了避免陷入局部极值，贝叶斯优化通常会加入一定的随机性，在随机探索和根据后验分布取值之间做出权衡。

本文采用贝叶斯优化方法，选择适合自适应光学系统迭代控制算法的超参数。分别以常用的SPGD、Momentum-SPGD 和CoolMomentum-SPGD控制算法为研究对象，以迭代优化控制算法的超参数作为输入，斯特列耳比（Strehl ratio，SR）值作为输出，采用贝叶斯优化选择合适的超参数。分析采用贝叶斯优化选择超参数的迭代控制算法的校正效果，并将校正结果与遍历法的结果进行比较。

1 自适应光学系统迭代控制算法

传统的随机并行梯度下降算法（SPGD）是美国陆军研究实验室的VORONTSOV M A 于1998 年提出[19]，随后被广泛研究[20-22]。SPGD 算法直接对光学系统的性能评价函数J进行优化。当前驱动器控制电压为 {uj}(j=1,···,N)，第n次迭代时，随机扰动 {δuj}(j=1,···,N)被并行施加到波前校正器的N个驱动器，此时系统性能指标的变化量为 δJ，SPGD 算法的迭代过程可以表示为

式中：γ为增益系数。本文采用斯特列耳比SR 作为性能评价函数J，用于表征畸变波前的校正效果[23]，性能评价函数J越接近于1，表示波前畸变校正效果越好。

随着深度学习的发展，越来越多的优化器被提出，并且已经成功与SPGD 算法结合用于自适应光学系统控制，如Momentum-SPGD 算法[7]、CoolMomentum-SPGD 算法[24]、RMSprop-SPGD 算法[10]和Adam-SPGD 算法[12]等。传统的SPGD 算法只有1 个超参数即增益系数 γ，Momentum-SPGD 算法和CoolMomentum-SPGD 算法有2 个超参数，分别是学习率和动量系数，表1 比较了3 种迭代控制算法的超参数。

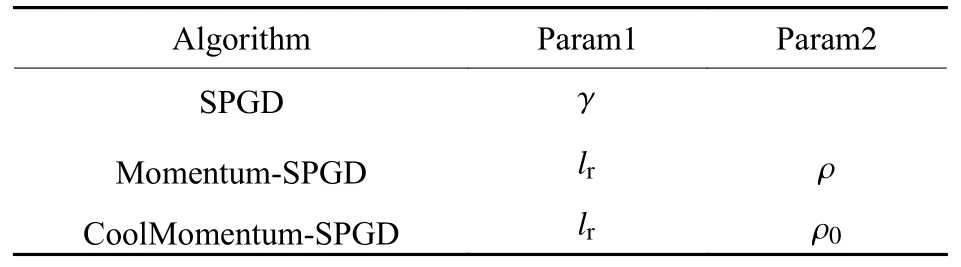
表1 不同迭代控制算法的超参数比较Table 1 Comparison of hyperparameter of different iterative control algorithms

2 超参数优化方法

超参数向量x到模型性能指标的映射记作f(x)，其中x∈Rd，超参数优化的目标是在超参数空间内寻找使得模型性能最优的d维超参数x*，记作：

在机器学习中，现有的超参数优化方法主要是网格搜索[25]、随机搜索[17]和贝叶斯优化方法[14]。贝叶斯优化方法只需要几个已知样本点，通过高斯过程回归计算已知样本点的后验概率分布，得到每一个超参数在每一个取值点的期望均值和方差。其中均值代表这个点最终的期望效果；方差表示这个点的效果的不确定性，方差越大，代表值要用更多的样本点去探索。

贝叶斯优化方法主要有两个核心：高斯过程回归模型和采集函数。高斯过程回归模型用于近似表示黑箱目标函数。令随机向量X=[x1,x2,···,xn]，服从多元高斯分布X～N(µ,Σ)，µ为方差，Σ为协方差矩阵，其中：X1=[x1,···,xm]为已知观测变量，X2=[xm+1,···,xn]为需要预测的未知变量，则：

均值和协方差矩阵为

根据贝叶斯公式：P(X2|X1)=P(X2)P(X1|X2)/∫P(X1|X2)P(X2)dX2可得X2的后验分布：

式中：µ2|1为预测的未知变量的均值；Σ2|1为预测的未知变量的协方差矩阵。采集函数用于估计在已知数据条件下最优点最有可能出现的位置，主要作用在于平衡探索与利用，使其既能利用先前的已知观测值加快收敛，又能探索决策空间中不确定性强的地方，避免陷入局部最优。

3 自适应光学系统迭代控制算法超参数优化

评价迭代控制算法时，既要考虑到迭代控制算法的收敛精度（迭代收敛后的SR 值），也要考虑到控制算法的收敛速度，因此将迭代过程中的SR 值加入性能指标，用SR0表示性能指标：

式中：SRinter表示控制算法迭代过程中的SR 值；SRend表示控制算法迭代结束后的SR 值；c表示权重系数。本文分别以迭代300 步、1 000 步时的SR值作为SRinter和SRend，c取值0.6。应根据具体应用的需求设定考察SR 值的步数、中间过程与结束时SR 值的权重。

本文以自适应光学系统迭代控制算法中的超参数作为贝叶斯优化方法中目标函数的输入，每组超参数对应的加权SR 值作为贝叶斯优化方法中目标函数的输出。先是获得初始点个数，对初始点进行高斯过程回归，预测出目标函数的曲线，本文高斯过程中核函数选择Matérn 协方差函数。然后选择合适的采集函数评估下一个采样点，常见的采集函数有概率提升函数（PI）、期望提升函数（EI）、置信上界函数（UCB）。采用单一采集函数的贝叶斯优化算法不可能在所有问题上都表现出最好的性能，因此，还有使用对冲策略组合多种采集函数的贝叶斯优化算法，比如GP-Hedge 算法[26]。本文为寻找目标函数最大值，采用置信上界作为采集函数：

式中：µ()表示数学期望；σ()表示方差；κ为调节参数，通过控制调节参数实现对探索未知和已知数据信息之间的平衡。采用概率提升作为采集函数：

式中：Φ()表示正态累积分布函数；ℓ是用来平衡探索和利用的随机参数；f(x+)表示现有的最大值。采用期望提升作为采集函数：

式中：z=(µ(x)-f(x+))/σ(x)表示对当前最优点取值的归一化。GP-Hedge 算法是在每次迭代中，把从每种采集函数得到的候选点组成候选点集合，然后根据对冲策略从候选点集合中选取评估点。此时，贝叶斯优化会猜测出一个或多个采集函数取得最大值的函数值，判断该结果是否满足结束条件，如果满足就结束优化过程，否则将此结果加入初始点，继续进行高斯过程回归，预测出新的目标函数曲线，再利用采集函数选出下一个采样点，直到满足结束条件。

采用贝叶斯优化方法选择超参数的具体实现过程如图1 所示。首先是确定域空间，在SPGD 算法中，超参数 γ的域空间为(0,6]，在Momentum-SPGD 和CoolMomentum-SPGD 算法中，超参数lr和ρ的域空间都为(0,1]；再设置加权SR 值作为性能指标；然后获得样本点（超参数值及其对应的加权SR 值），对样本点进行高斯过程回归，获得目标函数的预测曲线，完成对超参数空间的建模；在每次迭代中，计算每个样本点的采集函数，即置信上界，并选择置信上界最大的点作为下一个采样点，即在超参数空间中选择一个新的点进行实验，得到其目标函数值，并将其添加到已有的样本点中。通过不断迭代更新模型和选择下一个采样点，直到达到结束条件（达到最大迭代次数），完成超参数的优化。

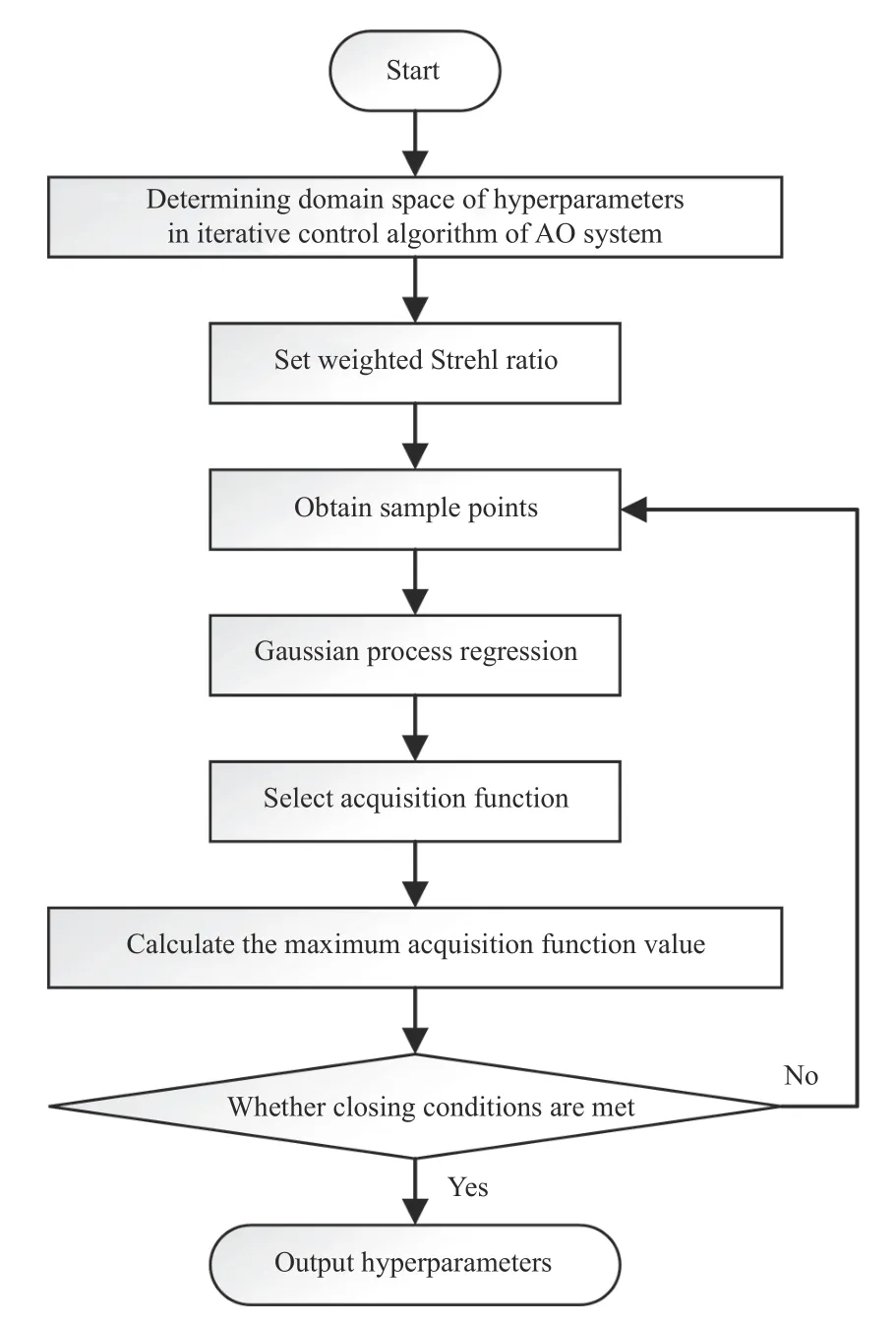
图1 自适应光学系统迭代控制算法采用贝叶斯优化方法选择超参数的实现流程Fig.1 Implementation flow of hyperparameter selection using Bayesian optimization method in iterative control algorithm for adaptive optics systems

4 结果与分析

模拟实验所用计算机为Windows10 系统，硬件环境为：11th Gen Intel(R) Core(TM) i5-1135G7 CPU，主频2.4 GHz，16.0 GB DDR3 RAM。模拟实验中采用François Assémat 提出的方法[27]生成相屏模拟待校正像差，生成的相屏统计属性符合Kolmogorov 谱，且相屏间不具有相关性。湍流强度大小用D/r0表示，D为望远镜的口径，r0为大气相干长度。本文在湍流强度D/r0=5的条件下随机选择1 帧相屏进行模拟实验。在贝叶斯优化方法中，采集函数为置信上界函数时，参数 κ设置为1；为概率提升函数时，参数 ℓ设置为0.1；随机探索步数为2，贝叶斯优化步数为10。在验证该方法对于迭代控制算法性能影响时，以SR 值达到0.8 时的迭代步数作为校正速度的评判标准，稳定收敛时达到的SR 值作为收敛精度的判断标准，以下3 种控制算法在迭代1 000 步时均已稳定收敛。

4.1 SPGD 算法超参数选取

SPGD 算法中有1 个超参数即增益系数 γ，以增益系数 γ作为输入，γ的取值范围为(0,6]，加权SR 值作为输出。图2 为SPGD 算法中迭代6 次后的预测目标函数图及其采集函数图，采样函数选择置信上界函数。图2（a）中圆点标记为采样点，虚线标记为预测的目标函数，阴影范围为95%置信区间。图2（b）中实线标记为采集函数，星形标记为下一个采样点。

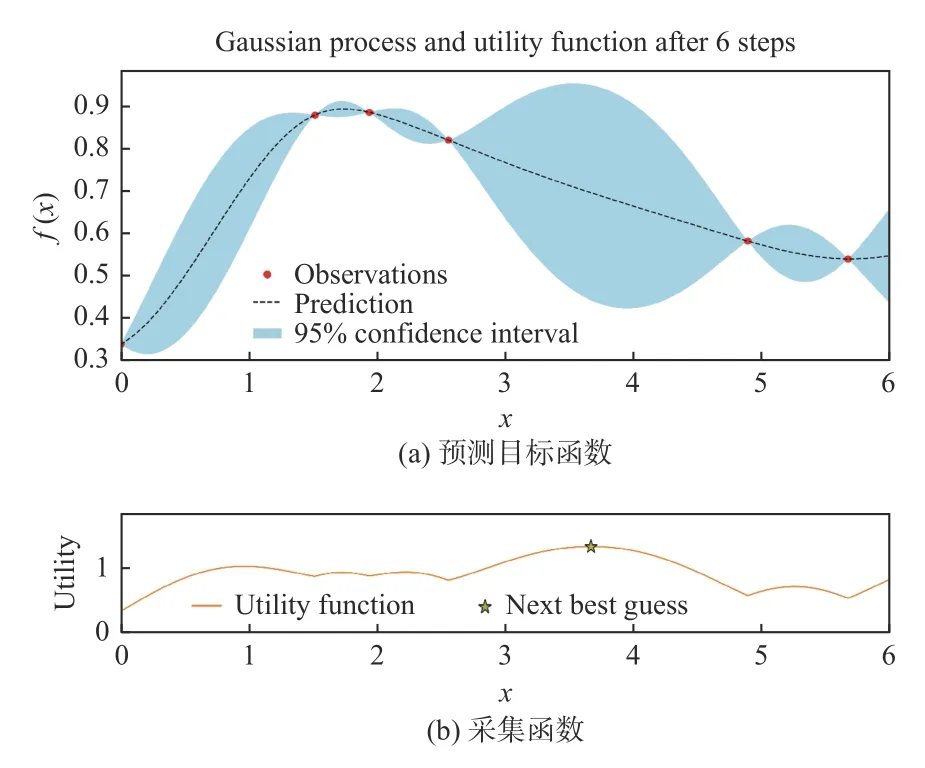
图2 SPGD 算法中迭代6 次后的预测目标函数图及其采集函数图Fig.2 Diagram of prediction objective function and its acquisition function after 6 iterations in SPGD algorithm

遍历法中 γ以0.1 为间距，在(0,6]范围内等间距取值共60 组超参数。从遍历法的60 组超参数中人工选取校正效果最理想的一组和贝叶斯优化方法进行对比，对比结果如表2 所示。表2 中贝叶斯优化方法采用了不同的采集函数。BO_UCB 表示在贝叶斯优化方法中采集函数选择置信上界函数，BO_PI 表示在贝叶斯优化方法中采集函数选择概率提升函数，BO_EI 表示在贝叶斯优化方法中采集函数选择期望提升函数，BO_GP 表示在贝叶斯优化方法中采用GP-Hedge 算法确定下一个采样点。BO_UCB 方法所需样本实例数量最少为6，BO_GP方法所需样本实例数量最多为10。在迭代到206步时，BO_GP 方法中的SR 值达到0.8，而BO_UCB方法需要迭代223 步；在迭代1 000 步后，BO_UCB方法中的SR 值达到0.924 4，而BO_GP 方法中的SR 值只有0.901 4。表明在贝叶斯优化算法中采用不同的采集函数对SPGD 算法的收敛效果是有影响的，其中BO_UCB 方法所需样本实例数量最少，迭代1 000 步后，SR 值最大。因此，在仿真实验中选取BO_UCB 方法与遍历法进行对比。从表2 可以看出，贝叶斯优化方法的样本实例数量是遍历法的10%，采用贝叶斯优化方法选择超参数的迭代控制算法，收敛速度和收敛精度均优于遍历法。

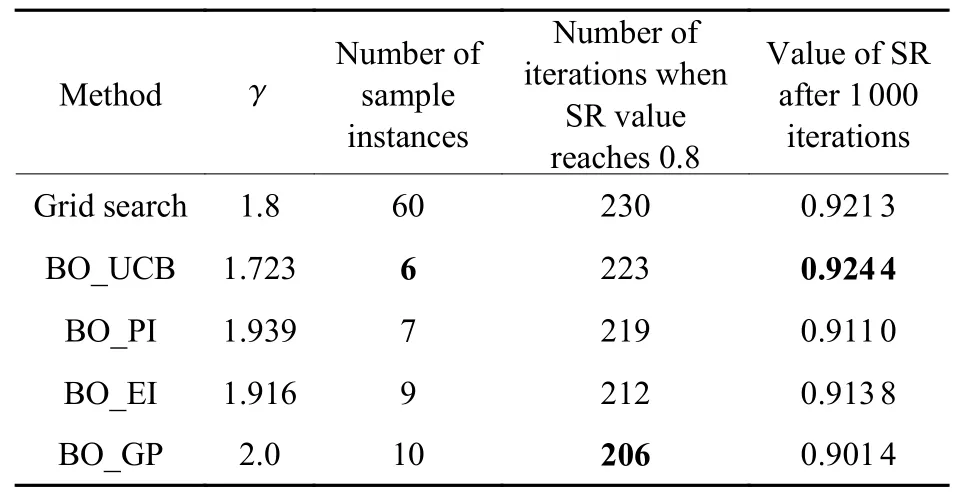
表2 SPGD 算法采用遍历法与贝叶斯优化方法选择超参数的结果对比Table 2 Comparison of results of SPGD algorithm using traversal method and Bayesian optimization method for hyperparameter selection

为了更直观地评价贝叶斯优化方法的性能，分别采用遍历法和贝叶斯优化方法选择超参数的迭代控制算法，收敛效果如图3 所示。图3 中虚线标记“--”代表贝叶斯优化方法，实线标记“-”代表遍历法，标记“-·”表示人工挑选的遍历法中校正效果最佳的3 组参数对应的SR 曲线。从图3 中可以看出，采用贝叶斯优化方法选择超参数的SPGD 算法在迭代到223 步时，SR 值达到0.8；迭代1 000 步后，SR 值达到0.924 4。结果表明，采用贝叶斯优化方法选择超参数的迭代控制算法不仅收敛速度较快，收敛精度也得到保障。

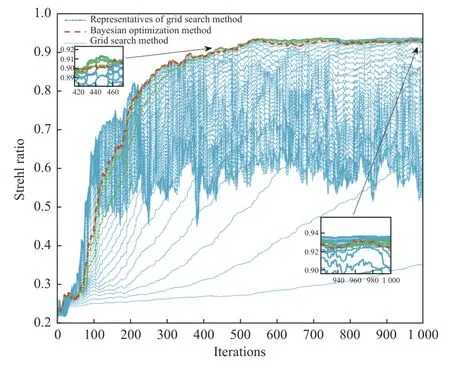
图3 采用遍历法和贝叶斯优化方法选择超参数的SPGD算法的SR 曲线Fig.3 SR curves of SPGD algorithm using traversal method and Bayesian optimization method for hyperparameter selection

4.2 Momentum-SPGD 算法超参数选取

Momentum-SPGD 算法中有2 个超参数，即学习率lr和动量系数 ρ，lr和 ρ的取值范围都为(0,1]。遍历法中lr和 ρ以0.1 为间距，在(0,1]范围等间距取值共100 组超参数。从遍历法的100 组超参数中人工选取校正效果最理想的一组和贝叶斯优化方法进行对比，结果如表3 所示。表3 中还给出了贝叶斯优化算法在采用不同采集函数时所需的样本实例数量，以及Momentum-SPGD 算法在SR 值达到0.8 时的迭代步数和迭代1 000 步时的收敛精度。贝叶斯优化方法的样本实例数量为7。从表3可以看出，贝叶斯优化方法在样本实例数量是遍历法的7%的情况下，采用贝叶斯优化方法选择超参数的迭代控制算法收敛速度优于遍历法，收敛效果和遍历法基本一致。

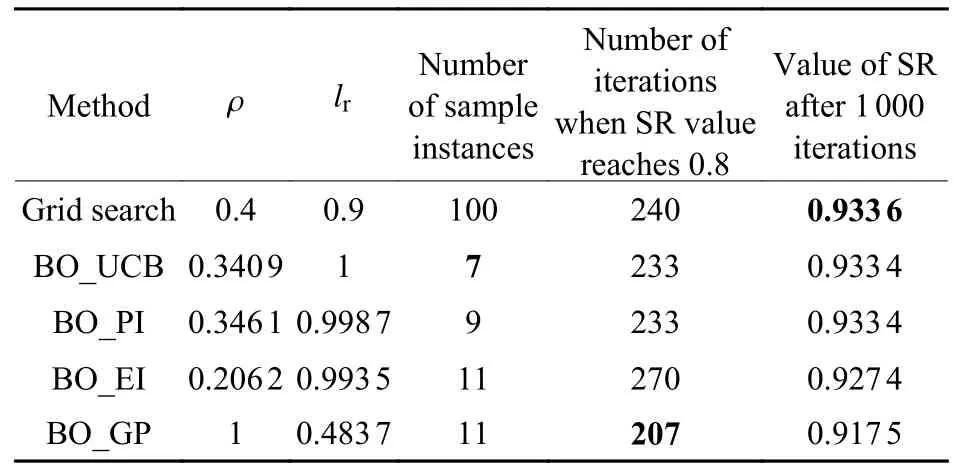
表3 Momentum-SPGD 算法采用遍历法与贝叶斯优化方法选择超参数的结果对比Table 3 Comparison of results of Momentum-SPGD algorithm using traversal method and Bayesian optimization method for hyperparameter selection

采用遍历法与贝叶斯优化方法选择超参数的Momentum-SPGD 算法收敛效果如图4 所示。从图4 中可以看出，采用贝叶斯优化方法选择超参数的Momentum-SPGD 算法在迭代到233 步时，SR值达到0.8；迭代1 000 步后，SR 值达到0.933 4。结果表明，采用贝叶斯优化方法选择超参数的迭代控制算法收敛速度相对较快，最终的收敛效果也较好。

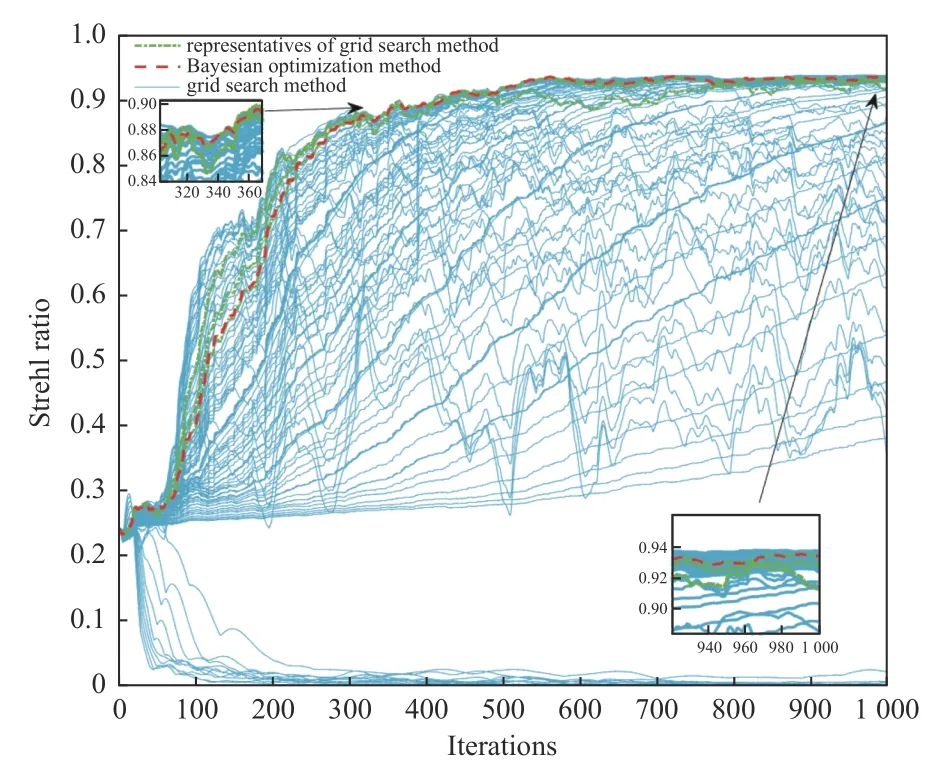
图4 采用遍历法和贝叶斯优化方法选择超参数的Momentum-SPGD 算法的SR 曲线Fig.4 SR curves of Momentum-SPGD algorithm using traversal method and Bayesian optimization method for hyperparameter selection

4.3 CoolMomentum-SPGD 算法超参数选取

CoolMomentum-SPGD 算法中有2 个超参数即学习率lr和动量系数 ρ0，lr和 ρ0的取值范围都为(0,1]。遍历法中lr和 ρ0以0.1 为间距，在(0,1]范围等间距取值共100 组超参数。从遍历法的100 组超参数中人工选取校正效果最理想的一组和贝叶斯优化方法进行对比，对比结果如表4 所示。表4 中还给出了贝叶斯优化算法在采用不同采集函数时所需的样本实例数量，以及CoolMomentum-SPGD 算法在SR 值达到0.8 时的迭代步数和迭代1 000 步时的收敛精度。贝叶斯优化方法的样本实例数量为9，是遍历法的9%。由表4 可知，采用贝叶斯优化方法选择超参数的迭代控制算法收敛速度和收敛精度上均优于遍历法。

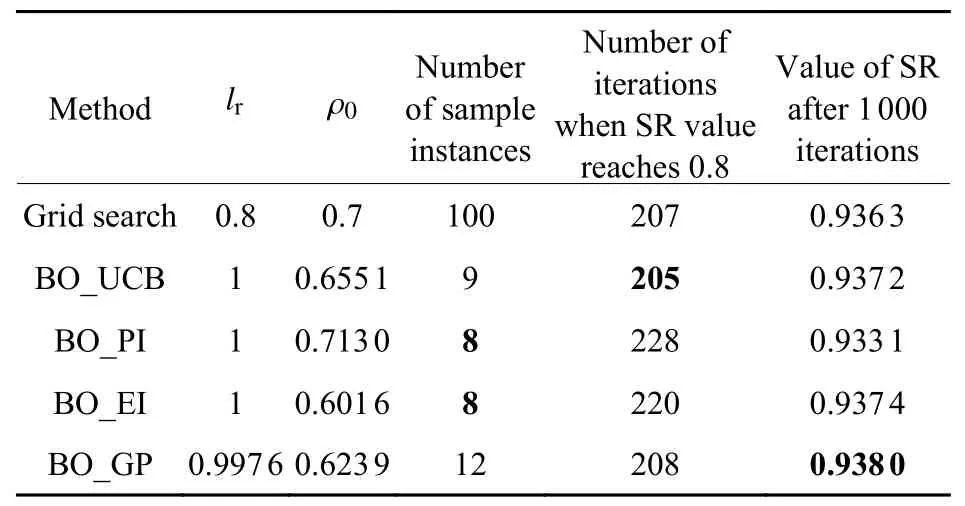
表4 CoolMomentum-SPGD 算法采用遍历法与贝叶斯优化方法选择超参数的结果对比Table 4 Comparison of results of CoolMomentum-SPGD algorithm using traversal method and Bayesian optimization method for hyperparameter selection

采用遍历法与贝叶斯优化方法选择超参数的CoolMomentum-SPGD 算法收敛效果如图5 所示。从图5 中可以看出，采用贝叶斯优化方法选择超参数的CoolMomentum-SPGD 算法在迭代到205 步时，SR 值达到0.8；迭代1 000 步后，SR 值达到0.937 2，结果表明，采用贝叶斯优化方法选择超参数的迭代控制算法收敛速度快，最终的收敛效果也相对较好。

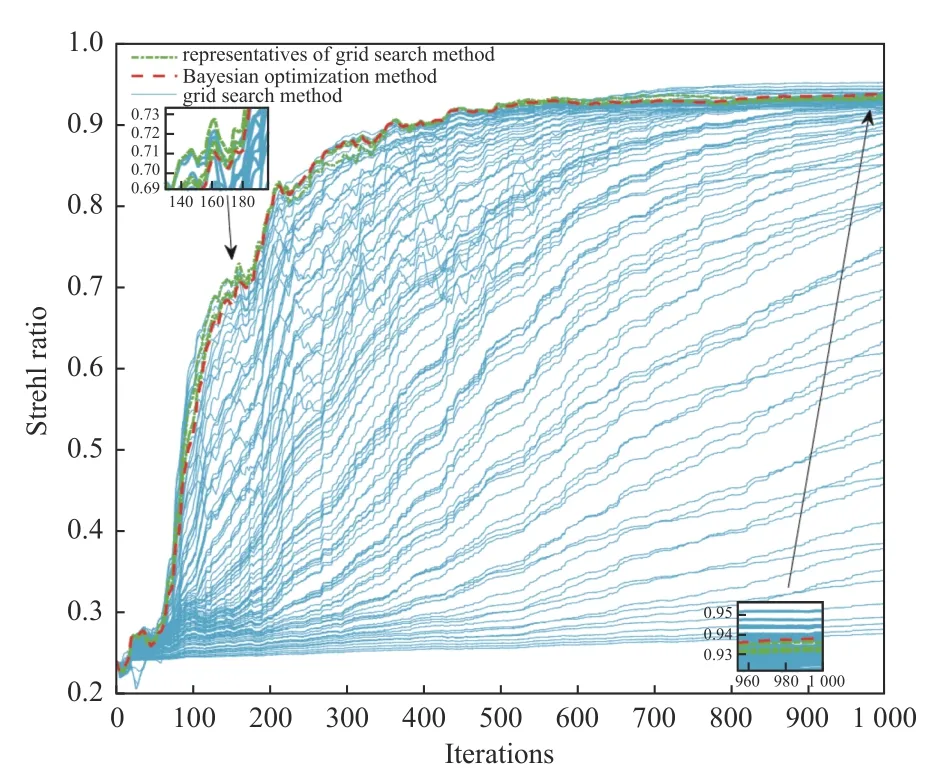
图5 采用遍历法和贝叶斯优化方法选择超参数的CoolMomentum-SPGD 算法的SR 曲线Fig.5 SR curves of CoolMomentum-SPGD algorithm using traversal method and Bayesian optimization method for hyperparameter selection

5 结论

在无波前探测自适应光学系统中，超参数的选择一定程度上决定着迭代控制算法的校正能力。现有的迭代控制算法的超参数设置一般采用遍历法，计算量大，耗时较长。本文提出将贝叶斯优化方法用于选择适合自适应光学系统迭代控制算法的超参数。分别以常用的SPGD、Momentum-SPGD和CoolMomentum-SPGD 控制算法为例，以迭代控制算法的超参数作为输入，斯特列耳比值作为输出，采用贝叶斯优化选择超参数。研究结果表明，对于SPGD 控制算法，取得相同收敛效果时，贝叶斯优化方法所需样本实例数量是遍历法的10%；对于Momentum-SPGD 和CoolMomentum-SPGD 控 制算法，贝叶斯优化方法所需样本实例数量分别是遍历法的7%和9%。且迭代控制算法本身超参数越多，采用贝叶斯优化进行超参数调优的优势越明显。后续将本方法拓展至超参数数目更多的迭代控制算法。本文研究结果可为自适应光学系统迭代控制算法的实际应用提供超参数设置理论基础。