基于小波变换的全息图压缩编码比较研究

付 泰，陈艾帅，胡 磊，桂进斌，吴佳雪，王晓诗，许路昕

（昆明理工大学 理学院，云南 昆明 650500）

引言

全息三维显示作为一种真三维显示技术，近年来成为三维显示领域的研究热点问题，被认为是未来最有前景的显示技术，同时将促进全息通信技术的发展[1]。记录三维场景的全息图包含了庞大的数据信息，其对通信的带宽及存储要求更高，全息视频图像压缩编码是促进全息三维显示及全息通信技术发展的必要工作[2]。由于全息图像素间的无关性，使用传统的二维图像压缩方法对全息图进行压缩，会导致全息图的压缩效率低和再现像失真，因此，全息数据压缩很有必要。

许多学者对全息数据压缩进行了研究[3-4]。近年来的国际研究[3]将全息压缩编码主要方法分为基于标准、基于量化、基于变换和其他特殊方式。基于标准的压缩方案中，XING Y 等[5]针对相移全息的问题，提出了一种基于JPEG2000[6]的自适应矢量提升方案，该方法压缩后的三维物体的重建质量优于传统方法。JIAO S 等[7]将JPEG 结合深度学习对纯相位全息图进行压缩，采用深度卷积神经网络来减少JPEG 压缩全息图中的伪影，该方法在减小原始全息图数据量的同时保证了重构图像的质量。基于量化的压缩方案中，SHORTT 提出[8]了将k-means 聚类分析应用到全息图的非均匀量化技术上，将聚类中心定位到距离质心最远的数据向量来处理空簇，获得了40 的高压缩比。基于变换的压缩方案中，NAUGHTON 等[9]将离散余弦变换(DCT)用于全息图压缩，再量化将不同区间的系数，然后通过编码进一步压缩。CHEREMKHIN P A 和KURBATOVA E A[10]提出了一种利用Meyer 和反向的双正交小波压缩离轴数字全息图的方法，通过阈值处理和量化对小波分解系数进行有损压缩，采用实部/虚部和振幅/相位压缩保证重建质量同时提高压缩比。HAJIHASHEMI V[11]提出了一种基于小波变换的数字全息系统(物面)HEVC 改进方法，利用小波变换减小复杂目标波场实部和虚部的大小，再结合最近邻插值和小波在图像大小调整中的不相似性来保持全息图的细节，实现了保持且略微提高信号保证度的同时，降低了BD 比特率。近年来许多学者还提供了利用深度学习的压缩全息图方案，HOU S 等[12]提出了一种量子激励神经网络中用于压缩CGH（computer-generated holograms，计算机生成的全息图）的优化初始权重方案，采用量子激励神经网络结构+带残差学习深度卷积网络并行对全息图像进行压缩，并且用优化的初始权重生成策略来加速压缩过程，该研究能够有效地降低压缩噪声，提高压缩CGH 的重建图像质量。KO H 等[13]提出了一种基于深度学习的纯相位全息图图像压缩网络框架DeepHolo，该网络通过数据增强技术以端到端的方式进行训练，并且以最小化输入全息图的熵为目标，BD(Bjøntegaard-Delta rate)速率增益超过了最新压缩标准视频编码39%。在上述全息图压缩研究中，使用小波变换获得了不错的压缩比和再现质量，通过小波变换多分辨率分析的特点，能够将全息图的高频和低频信息分离，方便对其进行有效的频域阈值，减少全息图像冗余。在小波变换中有很多小波基，研究如何选择小波基对全息图进行压缩编码，具有指导意义。

本文基于离散小波变换和图像压缩理论，使用小波阈值和量化的方法有损压缩全息图，对比分析使用不同小波基阈值对全息图再现像质量和全息图压缩比的影响。分别对振幅型离轴数字全息图和相息图进行压缩，通过仿真数据分析实验使用不同小波基对全息图的空域和频域进行阈值压缩处理，再进行数值全息重建。由于小波阈值只能改变全息图系数矩阵的系数值大小，并不能减小数据量，因此对处理后的全息图进行量化和用Huffman 编码对数据进一步压缩。

1 压缩原理及步骤

1.1 振幅型数字全息图及相息图

为验证方法的适用性，本文使用振幅型离轴数字全息图和相息图两种全息图进行测试。

离轴数字全息图是使用与物光场有一定夹角的参考光记录的数字全息图[14-16]，如图1 所示，激光照明位于 (x0,y0)平面的物体，物光波衍射到位于(x,y)全息记录面上时复振幅分布为O(x,y)：

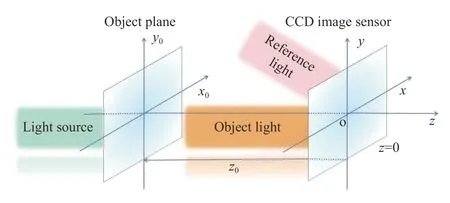
图1 离轴数字全息图记录示意图Fig.1 Schematic diagram of off-axis Fresnel digital hologram recording

与z轴负方向夹角为 θ的平面参考光R在全息图记录面相干涉，此时参考光的复振幅分布为R(x,y)：

全息记录面上对应的光强分布I(x,y)表示为

式中：2πay和 ϕ0表示参考光波和物光波在全息图平面的相位分布，参考光沿y轴方向空间频率a=(sinθ)/λ。最后在CCD 接收面上记录数字全息图。

相息图因其光轴方向只有单个重建像、衍射效率高受到高度关注，在三维显示及光场调控中获得广泛应用。本文使用Gerchberg-Saxton(GS)算法生成相息图[17-18]，利用空域和频域之间正反傅里叶变换与空域和频域的约束条件，反复迭代30 次，最后生成本文使用的相息图。

GS 算法具体步骤如下文。首先对n-1 次迭代的结果进行傅里叶变换，并保持得到的频域相位不变，振幅归一化：

其次对归一化频域分布进行逆傅里叶变换：

最后保留逆傅里叶变换后的相位信息，将振幅分布替换原图像振幅g0(x,y)，并将所得结果代入上一步骤，即对更新的值进行傅里叶变换：

1.2 基于小波变换压缩原理

小波变换[19]是将一个信号分解成由基小波φ(t)经过移位和缩放后的一系列小波。由于连续小波变换，尺度和平移系数会连续取值，产生巨大计算量，且图像为系数矩阵，因此本文使用离散小波变换，对信号f(t)进行离散小波变换的表达式如式（7）：

式中：〈〉表示内积；φj,k(t)表示离散小波函数。如图2所示，从滤波的角度来看，小波分解是根据小波基函数及以对应的尺度函数得到相应的高低通滤波器（小波系数矩阵），将小波基对应的高通和低通滤波器在时域与图像进行卷积，得到高频系数HL、LH、HH 和低频系数LL，再对低频系数LL 多次小波分解，得到如图2(b)所示的金字塔式结构，其中高频系数描述了原始图像的细节信息，低频系数则描述了图像的基本信息。使用不同的小波基进行小波分解得到的系数，在表示图像的基本和细节信息时会存在差别，本文所涉及的全息图压缩是对各尺度上的信息进行处理，因此需要找到合适的小波基对目标全息图进行表示。

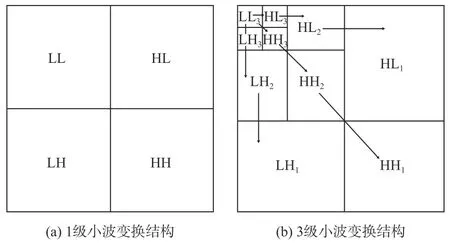
图2 二维小波分解Fig.2 Two-dimensional wavelet decomposition

目前4 种常用的不同类型的小波分别是：Haar、Daubechies、Symlet 和Biorthogonal 小波系[20-22]。

Haar 小波是最简单的具有紧支撑的正交小波，因为它只有一阶消失矩，所以不太合适逼近光滑信号。基函数的定义如（8）式：

而Daubechies 小波是实的紧支正交小波基。在任意给定的消失矩p下，满足F0(ejω)，并通过小波函数如式(9)所示，求出低通滤波器h={h0,h1,···,h2p-1}，从而构建出Daubechies 小波。由于Daubechies 小波不具有对称性(非线性相位)，所以对图像分解和重构时会产生一定的失真。

Symlet 小波是双正交小波，为通过对Daubechies 小波中F0(ejω)做选择优化而得到的具有近似对称的小波，在一定程度上减少了对图像进行分解和重构时的相位失真，其具有p阶消失矩和支撑长度[-p+1，p]。

为了解决对称性和对图像分解产生的失真问题，引入了双正交Biorthogonal 小波，它使用两个对偶的小波分别用于图像信号的分解和重构。在JPEG2000 压缩标准中，默认的无损图像压缩使用的小波滤波器为(5-3)小波滤波器，即bior2.2 小波基，而有损图像压缩默认的小波滤波器为(9-7)小波滤波器，即bior4.4 小波基。

本文采用对全息图小波阈值压缩的方式压缩全息图数据，即对分解后的金字塔式系数矩阵选取合适的阈值，小于该阈值的系数全部归零，从而增加系数中零的个数，达到信息量减少的目的，实现压缩全息图像数据。

1.3 全息图的压缩步骤

本文基于二维小波变换对全息图进行压缩，采用小波阈值、均匀量化和Huffman 编码3 个步骤对全息图进行压缩编码。

1）首先分别对全息图空域数据和全息图频域数据进行小波分解，并对小波系数赋予阈值。分别对全息图空域数据和全息图频域数据进行3 层小波变换，通过设定阈值方式，将小波系数中小于阈值的系数取值为零，大于阈值的系数保留。其中，小波阈值方法有全局阈值和分层阈值，这里选择全局阈值，即所有系数使用同一个阈值进行系数处理。由于硬阈值处理能更多地保留真实信号的峰值特征，阈值处理时采用硬阈值方式，具体表达式如下：

2）其次对全息图数据进行量化处理。对全息图系数矩阵进行均匀量化处理，首先得到系数矩阵内值的取值范围 [xmin,xmax]，然后依据取值范围划分为M=2N个区间，将系数矩阵分别量化为量化系数4、8、16、32 的全息图数据，其中量化间隔为 Δ，如公式(11)所示。将系数矩阵中在相应量化间隔内的系数取为固定值，虽然会导致信息丢失，但是数据复杂度降低，量化方式简单利于实现，且方便进行下一步Huffman 编码。

3）最后对有损压缩后的系数进行熵编码。使用无损数据压缩的熵编码（Huffman 编码），对上一步处理后的全息数据进行编码，每种不同的像素值对应一种码字，并将对应关系记录在码表中，最后全息数据全部被码字所代替形成字符串。

压缩方法的示意图如图3 所示。

图3 全息图压缩流程图Fig.3 Flow chart of hologram compression

2 仿真实验

本文的测试图像是反射式振幅型离轴数字模拟全息图和计算机迭代30 次生成的相息图。一般二维图像的压缩是针对图像的空域进行有损压缩处理的，由于全息图的空域像素间相干性特点，全息图频谱中的高频和低频信息包含了原物场的大部分信息，使用小波变换对全息图的频谱进行阈值有损压缩，与空域处理的结果作为对比。

采用的光源光波波长为632.8 nm，物到全息记录面的距离为0.5 m，CCD 面阵尺寸为5 mm，参考光角度为0.78。模拟生成的离轴数字全息图的具体步骤如下：

1）调入输入图像，将图像的大小调整为512×512像素；

2）采用模拟物光场，并与一定角度的参考光相互干涉得到全息图；

3）通过再现模拟算法得到全息再现像；

高职院校是军队优质兵员的战略储备基地，有义务、有责任做好大学生应征入伍工作，退役复学高职生就是学校征兵工作的最佳代言人。退役复学高职生参与学校征兵宣传工作、入伍咨询工作、军营生活解读工作、军事训练展示工作，具有明显的优势[3]。他们熟悉军营，熟悉军事训练，能带动更多的有志青年投笔从戎，为保卫祖国尽一份力，为部队改善兵员素质、提高兵员质量做出应有的贡献。

4）有损压缩编码后的全息图，再重复步骤3）可得压缩后再现像。

相息图的具体生成步骤如下：

1）调入图像作为振幅信息，大小为624×678像素；

2）计算机生成随机相位矩阵作为相位信息，大小为 624×678像素；

3）使用GS 迭代算法迭代30 次，得到原始相息图；

4）傅里叶逆变换相位得到相息图再现像；

5）有损压缩编码后的相息图，使用步骤4）可得压缩后再现像。

反射式的振幅型离轴数字与相息图模拟生成的图像如图4 所示。

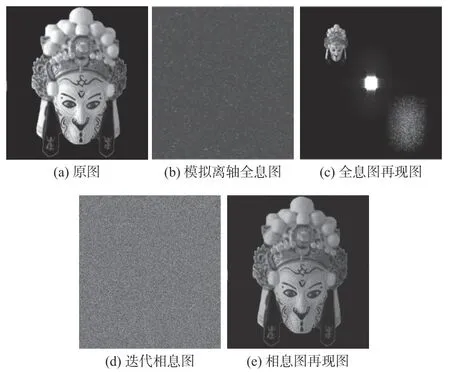
图4 全息图模拟Fig.4 Holographic simulation

比较压缩后的全息图再现像与原始全息图再现像的峰值信噪比(PSNR)，原始全息图的存储字节大小与Huffman 编码后数据流存储大小比值为压缩比。

2.1 离轴数字全息图压缩对比分析

本文对振幅型离轴数字全息图的空域、频域的实部和虚部以及频域的振幅和相位分别进行阈值压缩后编码处理。为了测试不同样式的离轴数字全息图压缩效果，本文分别对简单图像（“光”字）和复杂图像（“京剧猴脸”图）进行压缩测试。

小波基阈值有损压缩处理简单图像离轴数字全息图如图5 所示，可以看出压缩后的离轴数字全息图仍然保留干涉条纹信息。

图5 离轴数字全息图压缩Fig.5 Compression of off-axis digital hologram

表1 展示了分别使用不同小波基压缩离轴数字全息图空域和频域后得到的再现像PSNR 和全息图的压缩比。由于每种小波基都对全息图的空域和频域分别进行了小波阈值和4 个等级均匀量化，将各量化等级中每种小波系中最高的PSNR 和最高压缩比C展现出来。

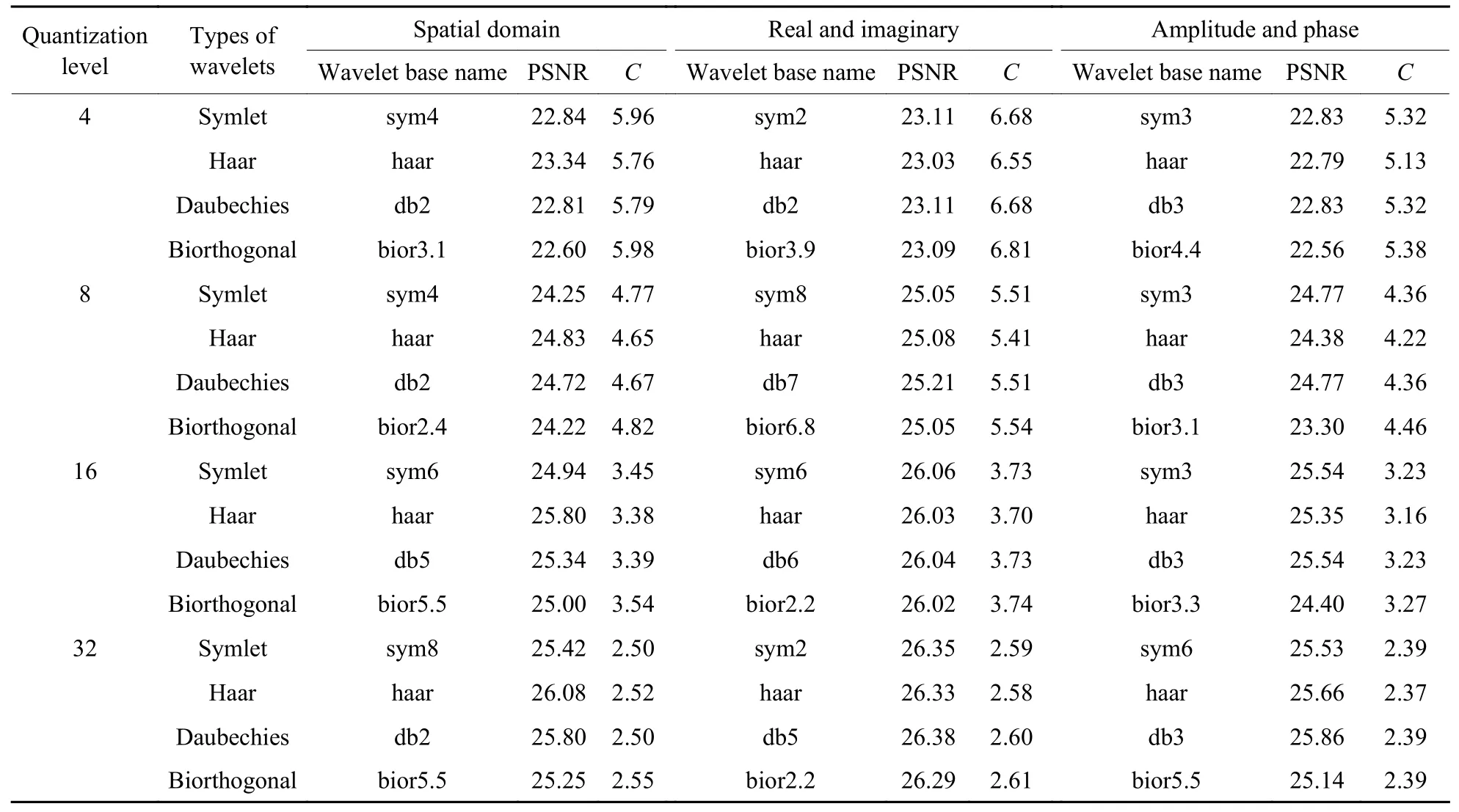
表1 离轴数字全息图不同小波基阈值再现像PSNR 和压缩比Table 1 PSNR and compression ratio of reconstructed image with different wavelet basis thresholds in off-axis digital hologram

从表1 中可以看出，压缩后的离轴数字全息图再现像质量会随着量化等级的提高而提高，其中对频域的实部和虚部进行压缩得到的再现像质量最高，在均匀量化等级为32 时，PSNR 达到了26 dB以上，对离轴数字全息图的空域压缩中，在同种小波系中，haar 和db2 小波基能够得到较好的再现像质量，其中使用db2 得到的再现像质量最好，量化等级为32 时，其PSNR 达到了25.80 dB；对离轴数字全息图频域的振幅和相位进行压缩时，在同种小波系中，haar 和db3 小波基能够得到较好的再现像质量，其中使用db3 得到的再现像质量最好，量化等级为32 时，其PSNR 达到了25.86 dB。

在保证较高再现像质量的同时，研究小波基对压缩比影响。随着量化等级的增加，压缩比随之降低，其中对全息图频域的实部和虚部压缩时，得到的压缩比高于对全息图的空域或者频域振幅和相位进行压缩。对全息图进行压缩时，使用Biorthogonal 小波得到的压缩比最高，能够得到更高的压缩比，如：bior2.2、bior3.9 和bior4.4 小波基。其中在全息图的实部和虚部进行量化等级为4 的压缩时，使用bior3.9 小波基，压缩比达到了6.81。

各类小波基阈值有损压缩处理简单图像离轴数字全息图的最高压缩比再现像和最高PSNR 图像如图6 所示。

图6 简单图像离轴数字全息图压缩前后再现像Fig.6 Reconstructed images before and after off-axis digital holography compression of simple images

由图6(b)和图6 (c1)可看出，在空域小波阈值有损压缩时，Daubechies 小波处理后的全息图再现像会出现缺失，而Haar 小波能保证重建图像完整，Haar 小波更适合用于空域阈值处理。

由以上测试结果可以得到如何选择使用不同小波基压缩简单图像离轴数字全息图。为了更好地在不同压缩全息图情况下选择合适的小波基，本文测试了小波基阈值有损压缩处理复杂图像离轴数字全息图所得的再现像。如图7，对于复杂图像同样有着较好的压缩效率和较高的重建质量。

图7 复杂图像离轴数字全息图压缩前后再现像Fig.7 Reconstructed images before and after off-axis digital holography compression of complex images

2.2 迭代相息图压缩对比分析

由于迭代相息图只将光波的相位信息编码到全息图中，以相位信息表示图像的振幅信息。相息图的特点完全不同于离轴数字全息图，对相息图的压缩更加困难，压缩比和重建图像质量会非常低，本文对相息图进行了初步测试。对迭代相息图的空域和频域进行了与离轴数字全息图相同的小波阈值有损压缩和量化编码测试操作。

由于相息图的特殊性，本文只选用各类小波最常用的小波基处理相息图。相息图通过小波阈值和量化编码处理后，得到的再现像PSNR 和压缩比情况如表2 所示，各类小波阈值处理后量化系数为8 的再现像如图8 所示。

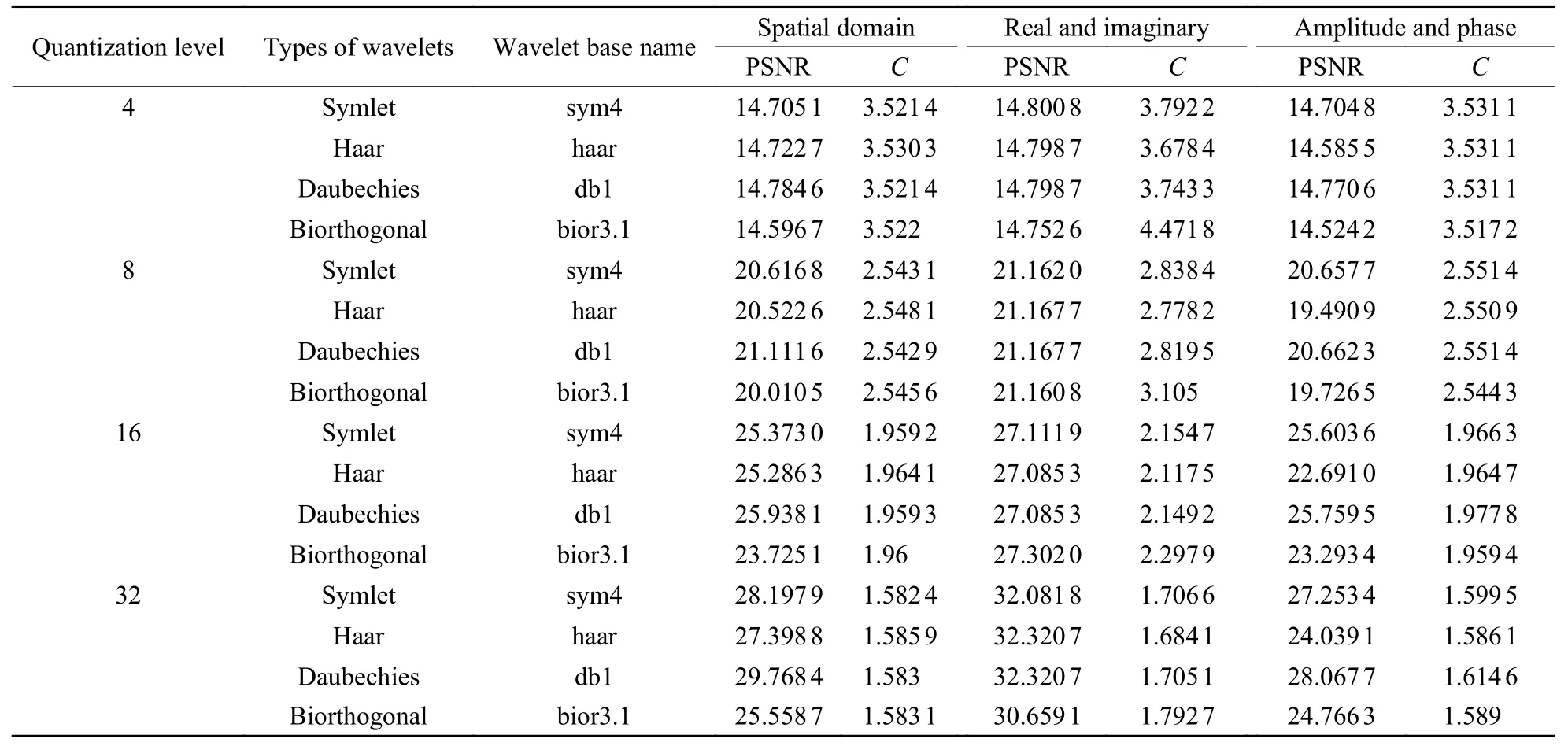
表2 相息图不同小波基阈值再现像PSNR 和压缩比Table 2 PSNR and compression ratio of reconstructed images with different wavelet basis thresholds in phase hologram

图8 小波阈值后相息图再现像(其中1、2、3、4 分别为使用sym4、haar、db1 和bior3.1 小波基)Fig.8 Reconstructed images of phase hologram after wavelet threshold (1,2,3 and 4 uses sym4,haar,db1 and bior3.1 wavelet bases respectively)

通过对相息图的频域的实部和虚部进行压缩，得到的再现像质量相对相息图空域压缩或者频域的振幅和相位压缩得到的再现像质量高。如表2 所示，对相息图的空域进行压缩时，Symlet 和Daubechies 小波能够得到较好的再现像，当量化等级为32 时PSNR 达到28.197 9 dB 和29.768 4 dB；对相息图的频域实部和虚部进行压缩时，Haar 和Daubechies 小波得到的再现像质量较好，当量化等级为32 时，其PSNR 达到了32.320 7 dB；对相息图的频域振幅和相位进行压缩时，Symlet 和Daubechies 小波得到的再现像质量较好，其中Daubechies 小波得到了最好质量的再现像，当量化等级为32 时，其PSNR 达到了27.253 4 dB 和28.067 7 dB。

相息图的压缩比情况如表2 所示，对相息图的实部和虚部进行压缩编码，得到的压缩比高于对空域或者频域振幅和相位压缩编码得到的压缩比，并且使用Biorthogonal 小波得到的压缩比存在明显优势，在量化等级为4 时，压缩比达到了4.471 8，量化等级为8 时达到了3.105 0。

图8 展示了相息图小波阈值和量化前后的再现像。经过压缩后的相息图再现像出现了噪声，其中对相息图的振幅和相位压缩得到的再现像噪声较少，再现像质量最优，而对相息图的实部和虚部进行压缩得到的再现像质量最差，噪声较多。

3 结论

本文基于离散小波变换和图像压缩理论，使用小波阈值和量化的方法有损压缩全息图，对比分析使用不同小波基阈值对全息图再现像质量和全息图压缩比的影响。分别对振幅型离轴数字全息图和相息图进行压缩，通过仿真数据分析实验使用不同小波基对全息图的空域和频域进行阈值压缩处理，再进行数值全息重建。经过测试分析，对离轴数字全息图小波阈值有损压缩后，Haar 和db5 小波基得到的再现像质量最高，其PSNR 达到了26.38 dB，使用sym2 和db2 小波得到的压缩比最高，达到了6.68。对迭代相息图小波阈值有损压缩后，Haar 和Daubechies 小波得到的再现像质量最高，其PSNR 达到了32.32 dB，使用Biorthogonal小波得到的压缩比最高，达到了4.47。经过对不同小波基压缩全息图分析后，为全息图小波压缩编码中小波基的选择提供新的思路，为小波变换压缩全息图用于显示和成像提供参考。