100 kHz 弹光调制器多功能调制仿真

刘燕霖，张 瑞，薛 鹏，陈媛媛，王志斌，李孟委

（1.中北大学 仪器与电子学院，山西 太原 030051；2.中北大学 山西省光电信息与仪器工程技术研究中心，山西 太原 030051；3.中北大学 前沿交叉科学研究院，山西 太原 030051）

引言

光偏振检测常用于测量目标的外形轮廓、表面粗糙度及边角特性等。近年来，光偏振检测在物理、偏振成像、通信传输、生物医学等多个领域具有广泛应用[1-4]。不同的调制方法下其偏振光测量精度不同。最早LIN J F 提出了一种利用旋转波片的斯托克斯检测法，通过矩阵运算实现对线偏振和圆形偏振特性的测量[5]。随后，LU S J 等人利用铌酸锂（LiNbO3）晶体的电光调制特性代替旋转波片，通过外部加载不同电压促使铌酸锂晶体对待测偏振光波进行相位调制，通过检测光强的变换进而求解出入射光的Stokes 参量[6]。接着，张颖提出一种带有补偿器的液晶相位可变延迟器，其主要通过调节驱动电压改变液晶双折射率，进而实现对偏振光相位延迟的调制[7]。与此同时，北京量拓科技有限公司提出椭偏测量技术，通过机械旋转补偿器改变光的偏振状态，从而实现相位延迟调制。但是，上述所研究的相位延迟调制技术均存在不足，例如液晶可变延迟器虽相位延迟量可调，但其快轴方向不可调，椭偏测量技术虽相位延迟量和快轴方向均可调，但快轴方向需要机械调制，转速较慢且结构较为复杂。

针对上述不足，本文提出一种具有更高相位延迟调制范围的圆型PEM，与上述的相位调制技术相比，具有光谱范围广（从紫外到太赫兹）、无机械运动部件、接收角范围大（≥80°）、有用孔径大等优点[8-12]。首先利用公式计算并仿真弹光晶体和压电驱动器的谐振频率，并详细分析得出弹光晶体和两压电驱动器的匹配频率，得到PEM 达到最佳振型时的谐振频率。接着，通过调节两压电驱动器的驱动电压的幅值与相位差，使PEM 实现纯驻波和纯行波两种特殊的调制模式。在这两种模式下，可实现快轴方向及相位延迟量均可调并且结构简单。同时，利用COMSOL 有限元仿真，通过模拟调节两压电驱动器的驱动电压的幅值与相位的比例，从而验证PEM 可实现多功能调制。

1 理论分析

PEM 结构简单并且调制效率高，是一个理想的相位延迟器。常见的PEM 为八角型单驱动[13]，为了增大PEM 在其光学孔径上的峰值延迟，满足更优的对称性结构，本文采用45°双驱动圆型PEM进行研究，如图1 所示。

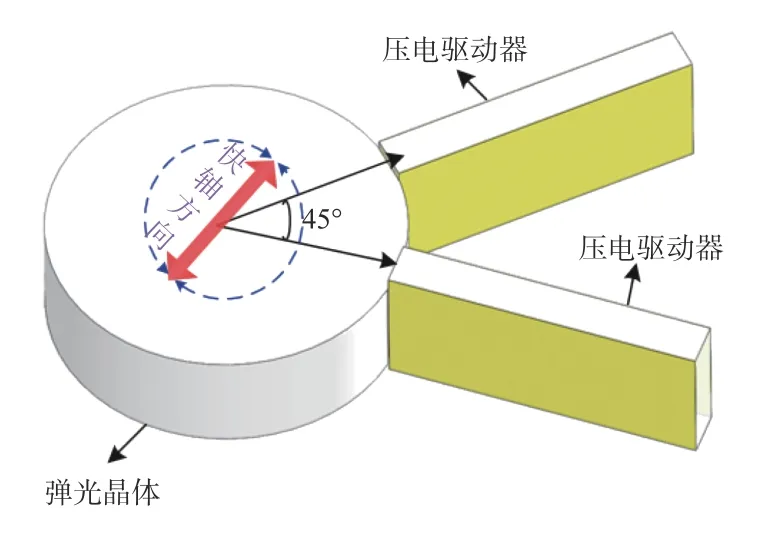
图1 100 kHz PEM 结构图Fig.1 Structure diagram of 100 kHz PEM

石英晶体具有稳定的机械性能，其介电常数和压电系数几乎不随温度而变化，并且其单一振动模态好，因此常用作PEM 的制作材料。压电驱动器选用压电石英晶体，具有特定切型且振动模态单一的特点，本文采用（xyt）-18.5°切型[14]。弹光晶体采用熔融石英晶体，具有纯度高及热稳定性高等特点，同时，在相同的驱动下，熔融石英的谐振频率较硒化锌的谐振频率更大，如图2（a）所示。因此，本文采用圆型弹光晶体，比八角型弹光晶体拥有更好的对称性，谐振时可达到更高的频率，如图2（b）所示。

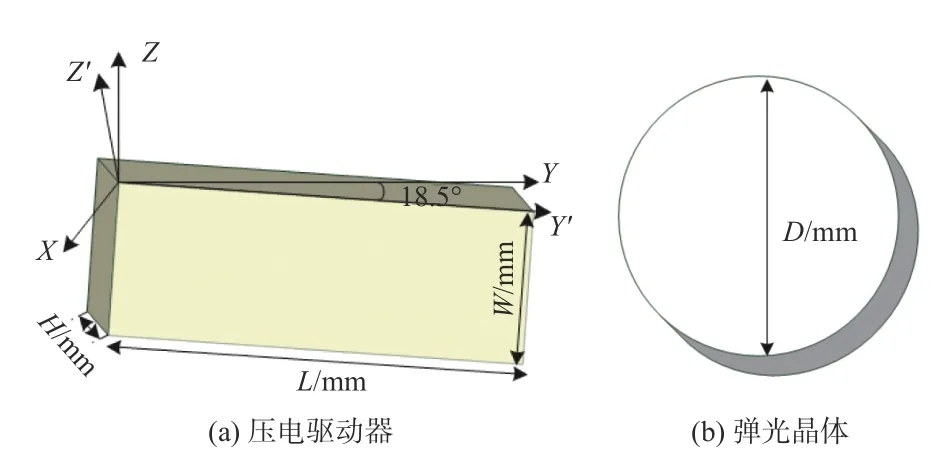
图2 PEM 组成结构Fig.2 Composition structure diagram of PEM

针对（xyt）-18.5°压电驱动器，其在交流电压作用下的振动频率[15]为

式中：A为压电驱动器长度；一般压电驱动器工作在基频模式下，即e=1；ρ为石英晶体密度，ρ=2.684 g/cm3；s22为压电驱动器的弹性柔顺系数，s22=1.4 454×10-11m2/N。通过计算，得到100 kHz 频率下压电驱动器的长度为25.38 mm。

在压电驱动器的驱动下，弹光晶体内两个方向的折射率发生变化，对应弹光晶体的谐振频率为

式中：P为杨氏模量，P=72.6×109Pa；ρ为熔融石英晶体密度ρ=2.201×103kg/m3；ε为泊松比，ε=0.16；L为弹光晶体的直径。通过计算得到，在弹光晶体的谐振频率为100 kHz 时，弹光晶体的直径为26.67 mm。

当压电驱动器振动频率和弹光晶体的谐振频率匹配时，PEM 达到共振状态，入射光垂直入射至弹光晶体，产生双折射现象，被分解为两束相互垂直的光分量，一束沿光轴方向，另一束沿垂直光轴方向。同时，两束光将产生相位延迟，进而改变入射光的偏振状态。通过PEM 的两束光分量之间的相位延迟为

式中：h是与应力成正比的常量；v0是驱动电压幅值；f是PEM 的谐振频率。

在上述分析中，光轴方向即为PEM 的快轴方向，PEM 的相位延迟量可由驱动电压进行控制，但就现有的PEM 来说，快轴方向均为固定方向，应用于光的偏振分析时，无法获得描述所有光的偏振态的斯托克斯矢量。因此，为解决快轴自动化的问题，应针对PEM 中的应力进行分析。

当压电驱动器振动时，会在弹光晶体中形成二维应力驻波，同时将这应力驻波在顺时针和逆时针方向分解成两列行波。由于采用两个压电驱动器进行驱动，因此在顺时针和逆时针方向均存在两列行波进行叠加，通过理论分析，进一步推导出不同驱动电压下的快轴方位角。

首先，将A 和B 中的驻波按照顺时针和逆时针方向分解，则在C 中的应力驻波为

接着，利用三角和函数公式将上式展开得到

将式（5）利用辅助角函数公式化简为

式中：SA=ρAVA，SB=ρBVB，ρA和ρB分别代表转换系数，与逆压电系数和耦合系数有关，VA和VB代表压电驱动器驱动电压的幅值；θ代表以x轴为参考的快轴方位角。，α代表两驱动电压之间的相位。

下面将讨论两种特殊情况，即弹光晶体中的应力只存在驻波和行波的情况。通过分析式（6）得到，当α=0 或π 时，弹光晶体的应力只存在纯驻波；当α=±π/2 时，弹光晶体中只存在纯行波。

当PEM 工作在纯驻波模式时，即α=0 或π，带入式（6）得到：

通过上述理论推导得出，当PEM 工作在纯驻波状态时，相位延迟与应力幅值成正比，快轴方位角可以通过调节两压电驱动器驱动电压幅值的比例进行改变，从而调制快轴方向，实现入射光斯托克斯矢量中全偏振参量的测量。虽然纯驻波模式下的PEM 可以实现快轴方向调制，但是仍需每次调节两驱动电压的幅值比例。针对此问题，提出纯行波模式下的PEM。

当PEM 工作在纯行波模式时，即α=±π/2，同时SA=SB时，带入式（6）得到：

式中：当 cos(ωt±2θ)=±1时，可推导得出快轴方位角θ；当α=+π/2 时，快轴方位角为 θ=，快轴沿顺时针方向旋转；当α=-π/2 时，快轴方位角为θ=，快轴沿逆时针方向旋转。此时，不难发现，快轴在做频率为f/2 的圆周运动，并且相位延迟量为常量。从而解决了之前所提出的问题，实现了PEM 在全偏振参量测量的突破。

2 PEM 纯驻波及纯行波仿真

2.1 PEM 弹光晶体及压电驱动器频率匹配仿真

当压电驱动器的振动频率和弹光晶体的谐振频率达到一致，PEM 达到共振状态，此时调制效率最高。根据上一节的理论公式推导得出，PEM 工作在100 kHz 频率下压电驱动器长度和弹光晶体直径分别为25.38 mm 和26.67 mm。为了验证PEM的共振频率，利用COMSOL 进行仿真。

压电驱动器的材料选用Quartz LH（1978 IEEE），设置旋转坐标系为（xyt）-18.5°。首先将压电驱动器参数设置为理论参数值，如表1 所示。利用特征频率求解器，求解出在理论压电驱动器长度下的特征频率值为98.349 kHz。可以看出，理论值和仿真值存在一定偏差，对此部分偏差考虑有以下几个原因：1）在COMSOL 中，建模时压电驱动器的材料选用COMSOL 自带的材料库中Quartz LH（1978 IEEE）材料，虽与理论值推导所用的材料系数（例如：石英晶体的密度、压电驱动器的弹性柔顺系数等）保持一致，但仿真时考虑到此材料中还包含其他材料属性系数（例如：介电常数、耦合矩阵等），对后续建模也会产生一定的影响；2）在利用COMSOL 进行分析时，需要对所建模型进行网格划分，网格细化的程度同样也会影响到模型的求解，网格细化程度越高，则所建立模型的误差越小。

表1 压电驱动器理论参数Table 1 Theoretical parameters of piezoelectric actuator

通过理论分析得出，在压电驱动器材料确定的条件下，压电驱动器的特征频率只与压电驱动器的长度有关。因此，通过COMSOL 对压电驱动器的长度以0.01 mm 步进进行参数化扫描，如图3（a）所示，得到振动频率为100 kHz 时压电驱动器长度为25.46 mm；压电驱动器在100 kHz 下的位移仿真如图3（b）所示。

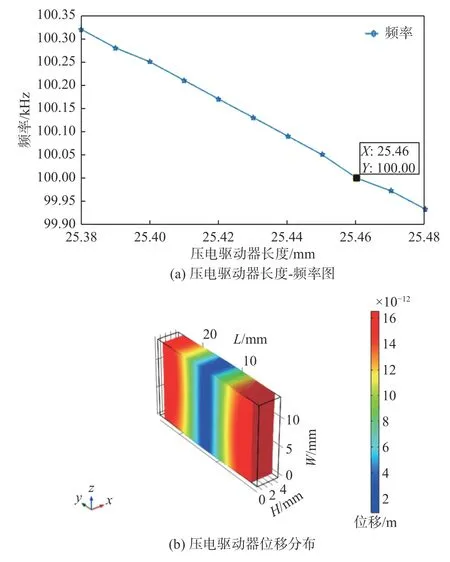
图3 压电驱动器稳态仿真结果Fig.3 Steady-state simulation results of piezoelectric actuator

弹光晶体的材料选用熔融石英，利用特征频率求解器，求解出在理论弹光晶体直径下的特征频率为100.53 kHz。同理，利用COMSOL 对弹光晶体的直径以0.01 mm 步进进行参数化扫描，如图4（a）所示，得到振动频率为100 kHz 时弹光晶体直径为26.81 mm；弹光晶体在100 kHz 下的位移仿真如图4（b）所示。

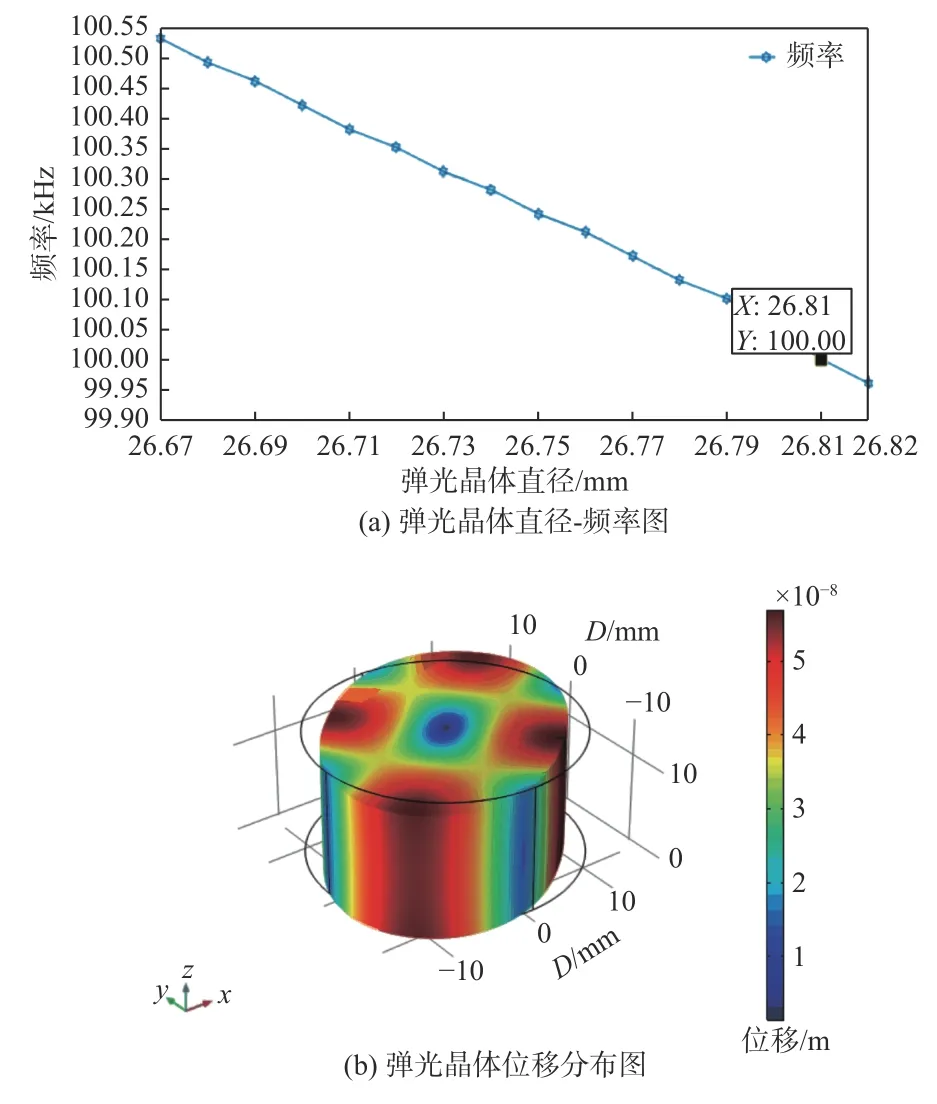
图4 弹光晶体稳态仿真结果Fig.4 Steady-state simulation results of elastic-optic crystal

经上述分析，得出在100 kHz 频率下，压电驱动器的长度为25.46 mm，弹光晶体的直径为26.81 mm，最终得到100 kHz 的谐振频率下，PEM 应力分布仿真图和位移分布仿真图如图5（a）、图5（b）所示。此时PEM 表面位移及应力分布高度对称，并且压电驱动器内部产生周期性稳定驻波，证明此时PEM 已经达到谐振状态。同时，分析得出在弹光晶体中心处的应力最大，位移变化最小。当光从弹光晶体中心通过时，调制效率可达到最大且相位延迟量最高。

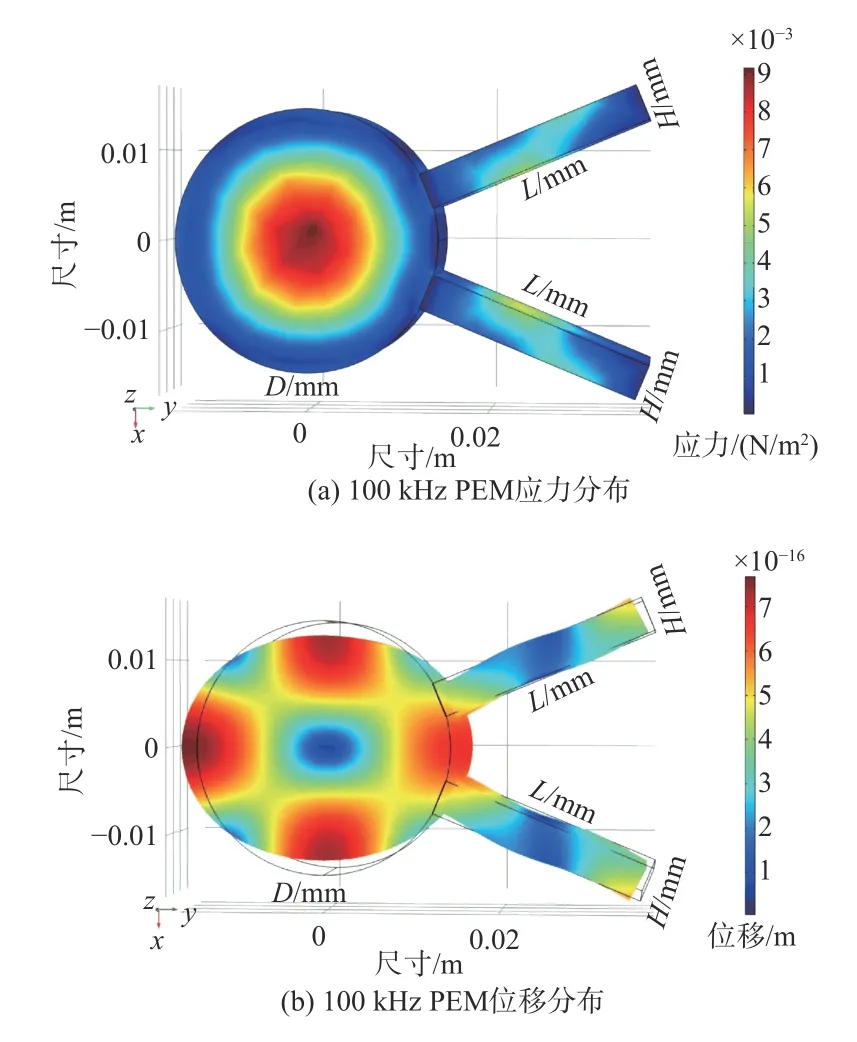
图5 100kHz PEM 稳态仿真结果Fig.5 Steady-state simulation results of 100 kHz PEM

2.2 PEM 纯驻波及纯行波仿真

通过上一节的分析，利用COMSOL 软件得到PEM 的谐振频率为100.02 kHz。根据理论分析，当PEM 工作在纯驻波模式下时，通过调节两驱动电压的幅值比例，可实现纯驻波模式下快轴方位角调节。在PEM 达到谐振频率的基础上，选用“压电”多物理场将“固体力学”物理场和“静电”物理场耦合，利用静电物理场中的“电势”模拟加在两压电驱动器两端的驱动电压，并按照理论分别调整两压电驱动器处电压的幅值比例。接着对所建模型进行网格化分析，此处需注意，在压电驱动器和弹光晶体连接处的网格分析需细化处理。最后利用瞬态求解器设置时间周期，进行模型求解。如图6 所示，基于PEM 的谐振频率，通过每次改变两驱动电压幅值比例，观测在不同比例的驱动电压下所对应的快轴方位角度。

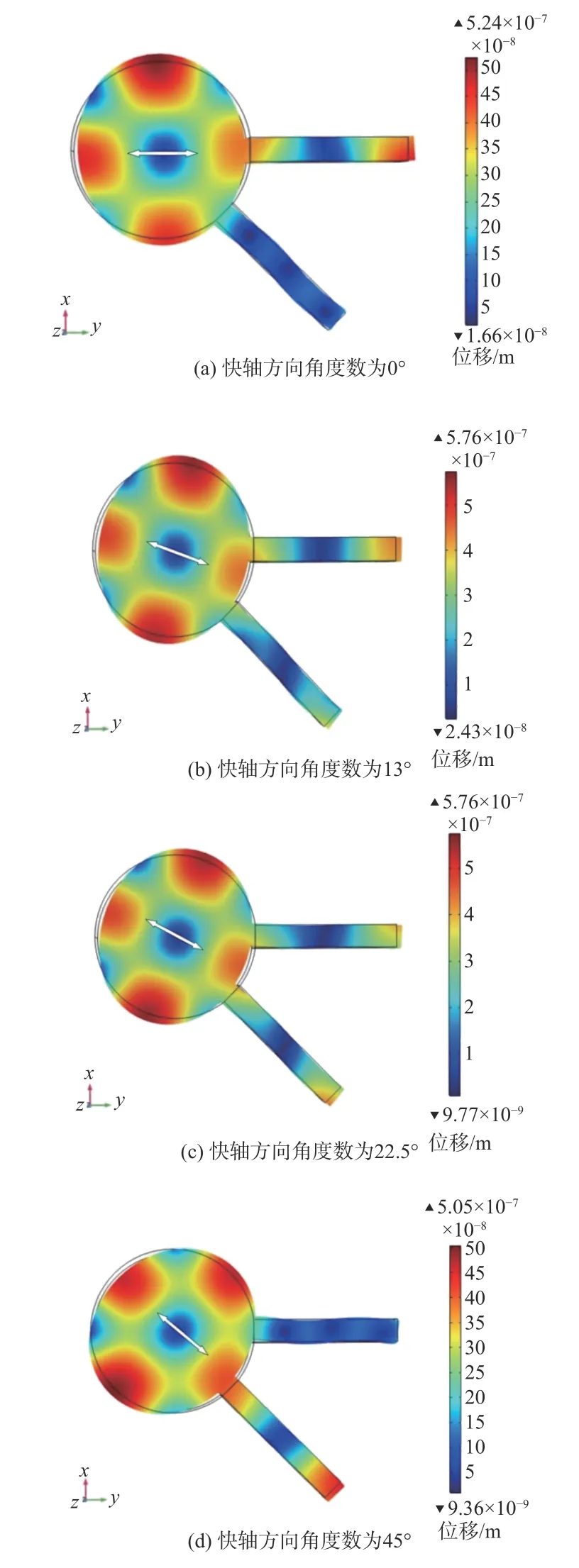
图6 PEM 四种纯驻波模式下的表面位移分布Fig.6 Surface displacement distribution diagram in four pure standing wave modes of PEM

在PEM 处于纯驻波模式的基础上，设置两压电驱动器的驱动电压幅值一致，相位相差π/2，利用COMSOL 仿真瞬态求解器，设置时间周期，选取步进为T/12 的一段时间间隔，即一个周期选取12 个点。此处，弹光晶体在两压电驱动器驱动下达到谐振频率需要一段时间，因此需要选取较长的时间周期，以进行纯行波模式求解，仿真结果如图7 所示。通过仿真结果可以看出，在PEM 纯行波模式下，快轴在一个周期内作圆周运动。

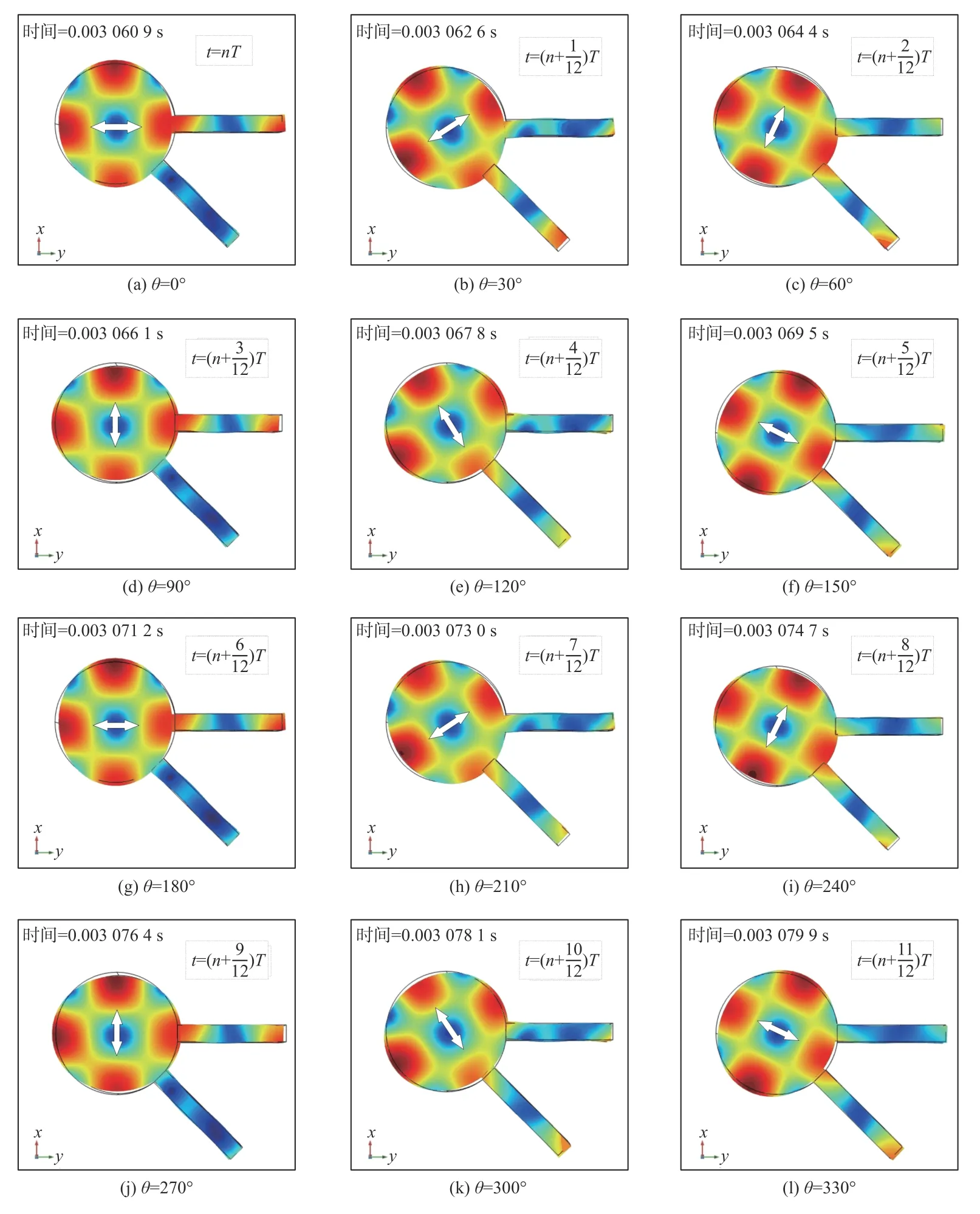
图7 100kHz 纯行波PEM 一周期表面位移分布图Fig.7 Surface displacement distribution diagram of 100 kHz pure traveling wave PEM in one period

由图7 可知，PEM 在纯行波调制模态时，快轴作周期圆周运动，同时压电驱动器作周期性的伸缩运动，压电驱动器的表面位移周期变换。并且无论快轴方向如何变化，弹光晶体中心处的位移变化量均为最小，并且应力最大。根据式（3）可知，相位延迟量与应力有关，因此弹光晶体中心的调制效率最高。

3 结论

通过COMSOL 仿真验证了两种特殊的PEM调制模式。对于纯驻波调制模式，可通过调节两驱动电压进而调节PEM 的快轴方向，从而改变光的偏振态；对于纯行波调制模式，相位延迟是一个常数，快轴作圆周运动，此种模式下，与旋转波片较为相似，通过傅里叶变换及反演得到光的斯托克斯矢量，可用于全偏振光领域，如椭偏仪测量样品的穆勒矩阵等研究。但本研究基于理论，运用COMSOL 仿真进行验证，是理想的情况。在实际实验过程中，还需要考虑一些误差对实验造成的影响，如两压电驱动器和弹光晶体之间的粘合而造成的残余应力双折射，以及在PEM 达到共振以后随时间产生温度漂移等问题，仍需进一步完善。