基于联邦集成算法对不同脱敏数据的研究

罗长银，陈学斌，张淑芬，尹志强，石 义，李风军

1.宁夏大学数学统计学院，宁夏 银川 750021

2.华北理工大学理学院，河北 唐山 063210

3.华北理工大学河北省数据科学与应用重点实验室，河北 唐山 063210

联邦学习自被提出以来一直是国内外相关研究的热点[1-2]，并且在众多领域都有很好的应用前景[3]。联邦学习的训练数据来自于不同的客户端，因此，训练数据的分布和数量是影响联邦模型的重要条件[4]。如果客户端的训练样本分布不同，则多个本地模型就难以集成[5]。为了解决这个问题，文献[6] 提出了一种联邦平均算法，它利用权重或梯度的平均值对多个本地模型进行集成，从而得到集成后的全局模型。但是文献[7] 针对联邦平均算法中的梯度更新提出了梯度深度泄露算法，能还原大部分的训练数据。

针对此问题，本文提出了在不同脱敏数据上的联邦集成算法，即根据不同的应用需求设置不同的参数，还原出的数据是不同程度脱敏后的数据。首先，该算法通过设置不同的变异率与适应度取值对数据进行脱敏，从而得到不同程度上的脱敏数据。其次，各客户端使用不同类型的全局模型在不同程度的脱敏数据上进行训练，根据其训练结果，选择合适的参数进行聚合。最后，使用加密算法对传输过程中的模型进行加密，以此来保护模型在传输过程中的安全性。实验结果表明，与联邦平均算法和传统集中式方法相比，stacking 联邦集成算法与voting联邦集成算法的准确率更优。在实际应用中，可根据不同的需求设置不同的脱敏参数来保护数据，以提升数据的安全性。

1 相关知识

1.1 联邦学习

在联邦学习中，常见的算法是联邦平均算法，针对联邦平均算法的精度问题，文献[8-9]利用统计学的方法来聚合多个本地模型，构建的全局模型的精度在非独立同分布上要优于联邦平均算法。同时为了检验不同联邦学习算法的性能，文献[10] 提出了使用贝叶斯检验的基准测试来衡量。文献[11] 提出了针对联邦学习开放应用程序的基准测试，主要研究各种指标之间的关系，如模型准确率与隐私保护预算之间的关系[12-13]。

1.2 遗传算法

遗传算法（genetic algorithm）是一种模仿自然界演化过程以寻找最佳解的方法[14]，也是根据生物种群优胜劣汰、适者生存的特点模拟出的随机搜索算法，交叉和变异操作是遗传算法中群体进化的主要操作[15]。

1.3 集成学习

集成学习指将多个弱监督模型结合在一起，从而建立一个更好更全面的强监督模型[16]。因集成学习构建的模型具有更高的准确率与鲁棒性等优点，所以集成学习被成功应用于解决语音识别、基因数据分析[17]、遥感数据处理[18]、图像处理、文本分类等众多实际问题。而在联邦集成领域中，经常使用stacking 集成算法、voting 集成算法、average 聚合算法、weighted average 聚合算法等来聚合多个本地模型。

2 基于遗传算法的联邦集成算法

2.1 算法的描述与流程

基于遗传算法的联邦集成算法包括数据处理和模型训练两个阶段。

在数据处理阶段的算法思想是各客户端在本地设置种群大小，并最大程度地对数据进行脱敏，根据脱敏前后向量的相似度来计算脱敏后数据的适应度情况，且对适应度的阈值进行了不同的设置，然后设置不同的变异率对数据进行变异，从而得到脱敏后的数据。

在模型训练阶段的算法思想是通过可信第三方将不同的初始全局模型传输至各客户端，并使用不同的集成算法来整合多个本地模型，得到更新的全局模型，且不断迭代训练。各客户端获取不同的初始全局模型，并在脱敏数据上进行训练，获取本地模型，各客户端将多个本地模型参数上传至可信第三方。

算法的流程如图1 所示。

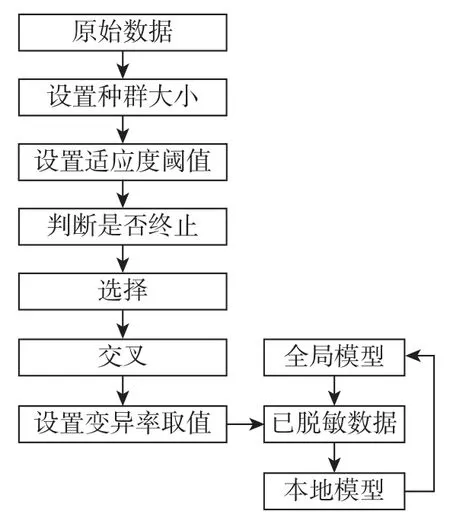
图1 不同脱敏数据上的联邦集成算法流程图Figure 1 Flowchart of federated ensemble algorithm on different desensitization data

2.2 性能分析

2.2.1 算法的复杂度分析

算法的复杂度分为全局模型传输、本地模型训练以及模型聚合3 部分组成，即时间复杂度为，其中：是5 种全局模型mj在客户端i上训练时的复杂度，l为本地模型聚合时的复杂度，n为数据脱敏时的复杂度，2k为模型传输时的复杂度。

2.2.2 算法的安全性分析

该算法通过调节不同的参数，对各客户端上的数据进行不同程度的脱敏，降低因梯度变化带来的数据风险，进而提升本地模型训练时数据的安全性。

3 实验分析

3.1 实验设置

本文所提的算法由python 与pycharm 软件实现。实验数据采用的是从https://www.heywhale.com/mw/dataset/5e61c03ab8dfce002d80191d/file 下载的数据集，该数据集来自于机器学习竞赛中的数据集，其中训练集中共有200 000 条样本，预测集中有80 000 条样本。

实验中数据预处理阶段的步骤如下：

步骤1将各客户端的待脱敏数据P0从右至左均分M份，每份为[P0/M]。当位数不足时，用0 补齐，得到初始种群S1={s1,s2,···,sm}，本文的种群大小参数[19]为M=8。

步骤2依据脱敏前后数据间的关联程度[19]将初始种群S1和遗传算法衍生的种群Sn用向量来表示，即(s11,s12,···,s1m) 和(sn1,sn2,···,snm)。用向量间的相似度来衡量脱敏的程度。用适应度阈值作为运算终止条件，适应度计算公式为

式中：适应度取值范围[0,1]，当满足终止条件f(S1,S2)＞x时，算法终止。因此，数据脱敏程度可通过x调节。适应度阈值的取值为x={0.25,0.50,0.75,0.90}。

步骤3客户端数据通过设置不同的变异率取值，来获取变异后的数据。变异率的取值范围为{0.1,0.3,0.6}。

3.2 实验分析

实验中模型训练阶段的步骤如下：

步骤1服务器将5 种初始模型类型与初始模型参数传输至客户端；

步骤2客户端获取模型类型与初始参数后，将初始模型在不同脱敏程度的数据上进行训练，获取本地模型；

步骤3客户端将本地模型传输至服务器；

步骤4服务器使用average 算法、stacking 集成算法、voting 集成算法聚合本地模型；

步骤5迭代步骤2～4，直至满足停止条件。

本文选取的初始模型类型为：随机森林、极端随机森林、神经网络、逻辑回归、梯度提升树（gradient boosting decision tree,GBDT）。根据模型训练的步骤进行训练，使用不同集成算法对本地模型进行聚合，获取不同的全局模型[20]。表1～5 依次是5 种不同初始全局模型在不同的适应度阈值与变异率下的实验结果，为表明实验数据的可靠性，表中的数据均为实验数据集随机划分且运行50 次后所得结果的均值。

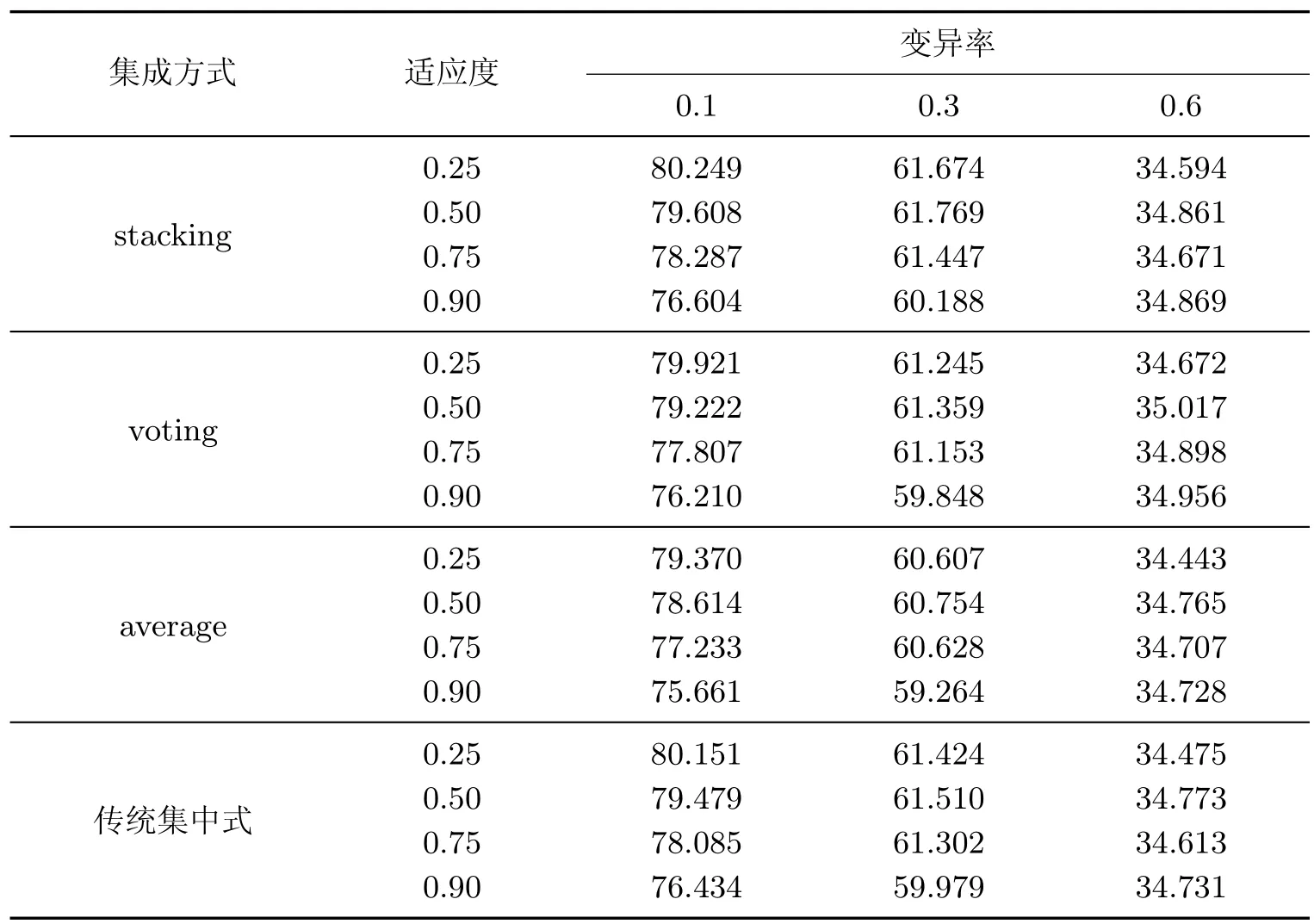
表1 初始模型为随机森林时，使用3 种集成算法与传统集中式方法的性能Table 1 Performance of using three ensemble algorithms and traditional centralized methods when the initial model is a random forest %

从表1 中可以得到，在3 种集成方式与传统集中式方法中，stacking 集成算法的准确率最高，剩下的依次是传统集中式方法，voting 集成算法和average 算法。其中，在stacking 集成算法中，当变异率增加时，模型的准确率逐渐降低；当适应度阈值增加时，模型的准确率也在逐渐降低。当变异率取0.1 且阈值取0.25 时，模型的准确率为80.249%，与传统集中式方法相比，准确率高0.099%，比voting 集成算法的准确率高0.328%，比average 集成算法的准确率高0.879%。

从表2 中可以得到，在3 种集成方式与传统集中式方法中，传统集中式方法的准确率最高，其次是stacking 集成算法，voting 集成算法，average 算法。其中，在3 种集成方式与传统集中式的方法中，当变异率增加时，模型的准确率逐渐降低；当适应度阈值增加时，模型的准确率也在逐渐降低。当变异率为0.1 且适应度阈值为0.25 时，传统集中式方法的准确率最高，为79.992%，stacking 集成算法的准确率为79.834%，stacking 集成算法的准确率略低于传统集中式方法。

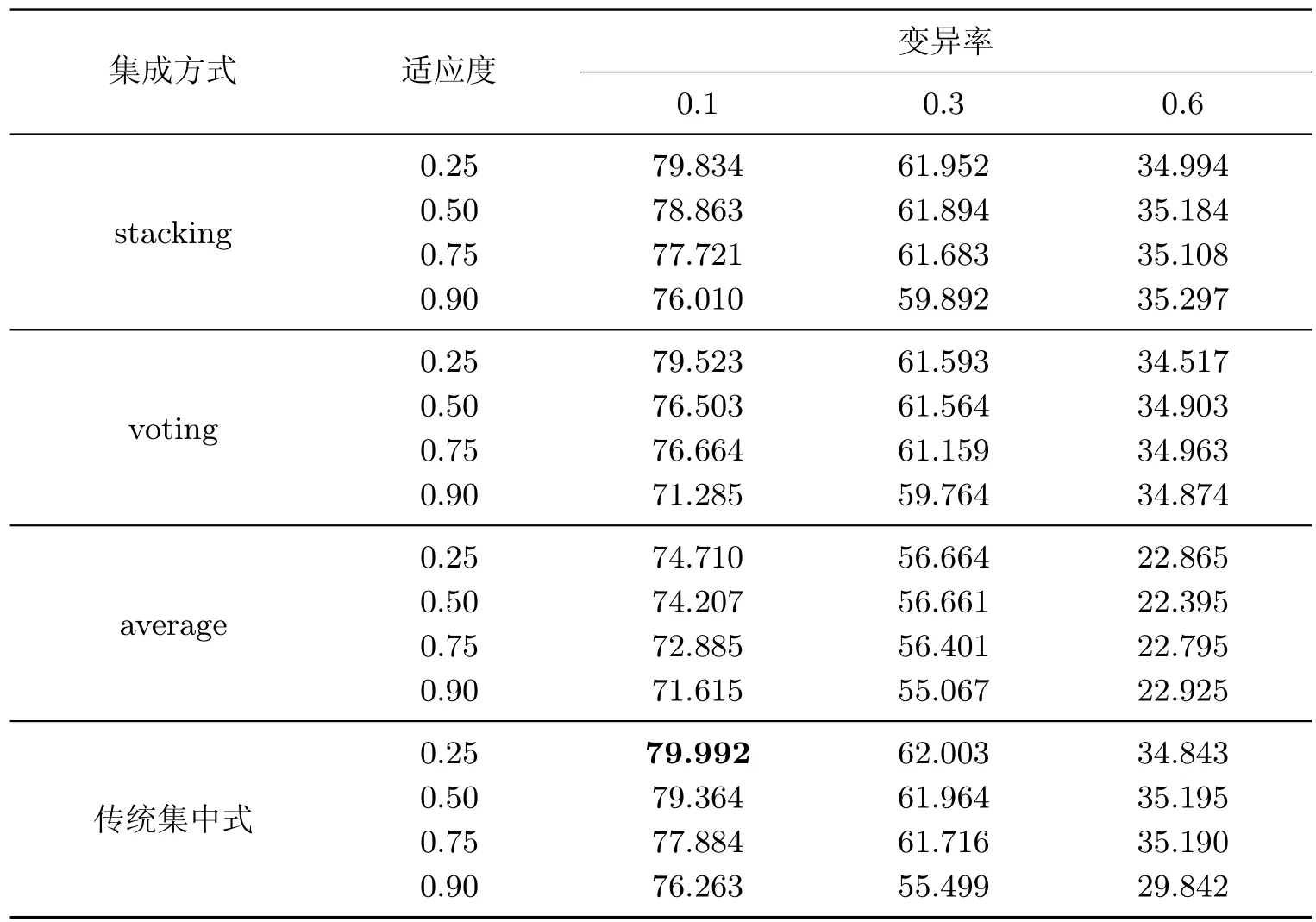
表2 初始模型为GBDT 时，使用3 种集成算法与传统集中式方法的性能Table 2 Performance of using three ensemble algorithms and traditional centralized methods when the initial model is a GBDT %

从表3 中可以得到，在3 种集成方式与传统集中式方法中，stacking 集成算法的准确率最高，剩下的依次是传统集中式方法，voting 集成算法，average 算法。在3 种集成方式与传统集中式方法中，当变异率增加时，模型的准确率在逐渐降低；当适应度阈值的取值增加时，模型的准确率也在逐渐降低。当变异率为0.1 且适应度阈值为0.25 时，stacking 建立的模型的准确率最高，为78.114%，比传统集中式方法的准确率高0.943%，比voting 集成算法的准确率高2.271%，比average 算法的准确率高0.437%。

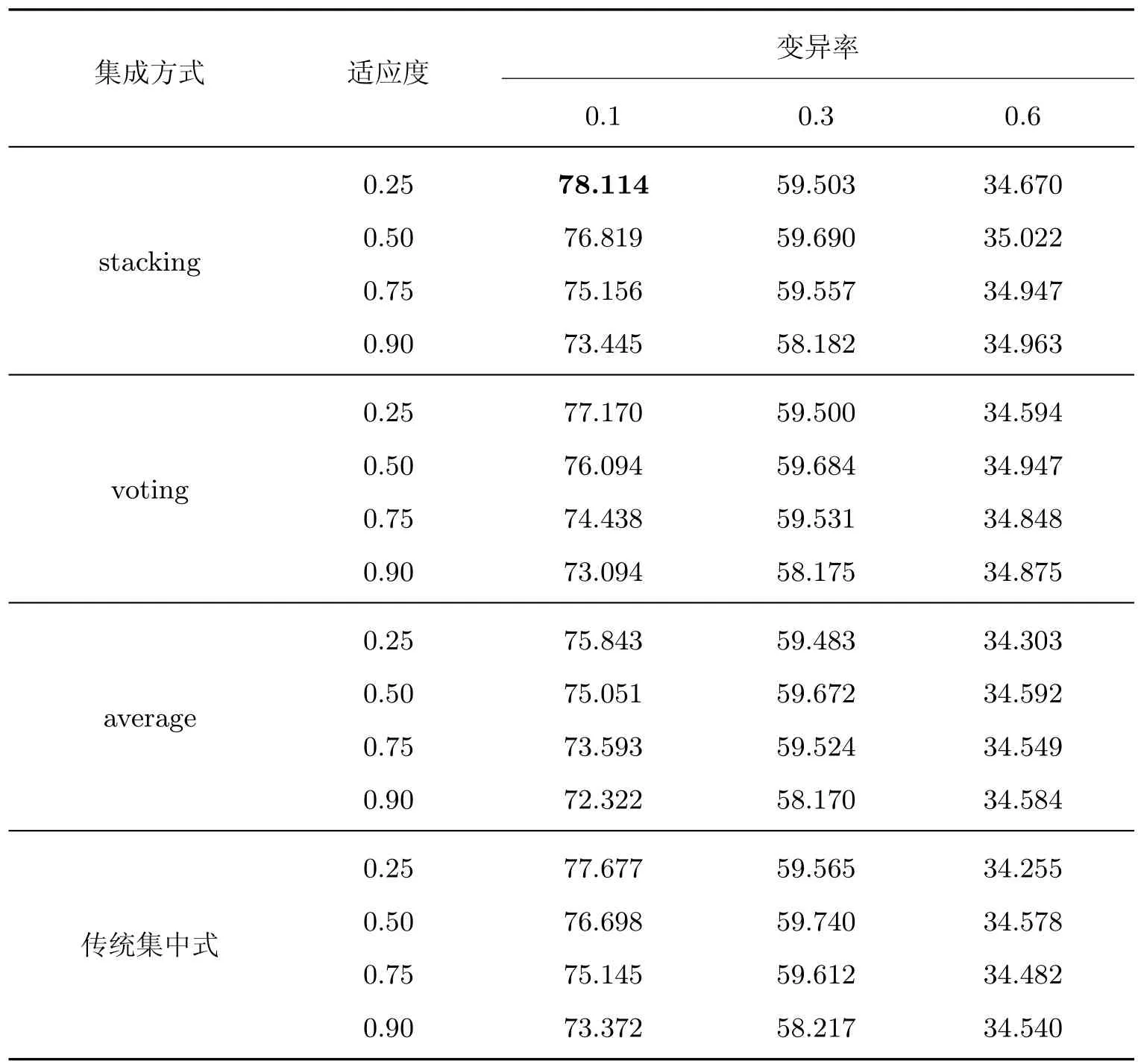
表3 初始模型为极端随机森林时，使用3 种集成算法与传统集中式方法的性能Table 3 Performance of using three ensemble algorithms and traditional centralized methods when the initial model is an extreme random forest %

从表4 中可以得到，在3 种集成方式与传统集中式方法中，传统集中式方法的准确率最高，其次是voting 集成算法，剩下的依次是average 算法和stacking 集成算法。其中，在3 种集成方式与传统集中式方法中，当变异率增加时，模型的准确率逐渐降低；当适应度阈值增加时，模型的准确率也逐渐降低。当变异率为0.1，适应度阈值为0.25 时，传统集中式方法的准确率最高，为75.069%，voting 集成算法模型的准确率为75.039%。

表4 初始模型为神经网络时，使用3 种集成算法与传统集中式方法的性能Table 4 Performance of using three ensemble algorithms and traditional centralized methods when the initial model is a neural network %

从表5 中可以得到，在3 种集成方式与传统集中式方法中，stacking 集成算法的准确率最高，其次是传统集中式方法，剩下的依次是average 算法和voting 集成算法。其中，在除average 算法以外的其他两种集成方式与传统集中式方法中，当变异率增加时，模型的准确率逐渐降低；当适应度阈值增加时，模型的准确率逐渐降低。当变异率为0.1，适应度阈值为0.25时，stacking 集成算法建立的模型的准确率最高，为75.125%，比传统集中式方法和average算法的准确率高0.002%，比voting 集成算法的准确率高0.035%。

表5 初始模型为逻辑回归时，使用3 种集成算法与传统集中式方法的性能Table 5 Performance of using three ensemble algorithms and traditional centralized methods when the initial model is a logistic regression %

3.3 实验小结

本文将遗传算法应用到客户端的数据脱敏中，通过调整适应度阈值与变异率取值，生成与原数据关联度不同的数据，进而获取不同脱敏程度的数据集。联邦学习框架中的模型在客户端的脱敏数据上进行训练，结合不同的集成算法来聚合本地模型，实验结果表明stacking集成算法与voting 集成算法建立模型的准确率要优于联邦平均算法，且与传统集中式方法的准确率几乎相等。同时本地模型是在脱敏数据上训练获取的，因此降低了梯度更新造成的数据泄露的风险。

4 结语

本文通过对适应度阈值和变异率采用不同取值来探索数据脱敏前后的关联性，关联性越低，准确率在降低；变异率取值越大，准确率也在降低。将不同的联邦集成算法在不同程度的脱敏数据上进行分析，联邦集成算法要优于联邦平均算法，同时降低了数据泄露的风险。