两自由度赫兹接触弹跳碰撞振动系统数值研究

◇兰州交通大学机电工程学院 穆 航

本文建立研究了一种两自由度赫兹接触弹跳碰撞振动系统模型，对其进行受力分析，列出方程并无量纲处理。选定参数使用Runge-Kutta法，对方程进行了数值积分，绘制了弹跳碰撞系统在一定的振动频率区间的分岔图、相图、庞加莱截面图，分析了其运动特征及分岔特性。同时研究了系统中弹跳间隙和接触刚度分配系数以及接触阻尼分配系数对系统运动特性的影响，发现为使系统运动稳定，弹跳间隙在合理范围内应取相对较大的值，接触刚度分配系数应取较小值，接触阻尼分配系数取较大值为宜。

1 引言

振动是一种人们在日常生活中无法忽视的现象，振动对于实际生产的影响既有利亦有害。人们根据振动的原理，在通信行业、工程里的防震、设备里的振动控制等各个行业中起到了重要作用。Shaw[1]通过定性分析和数值模拟，为研究具有间隙和约束的机械系统的动力学奠定了基于冲击的庞加莱映射基础。Long[2]研究了由谐波冲击器运动激励的弹性结构的非光滑动力学，并探索了导致非周期运动的机制。Li[3]研究了质量-弹簧-皮带摩擦自激振动系统的分岔特性和控制。Machado M[4]根据赫兹理论使用Kelvin-Voigt的接触力模型提供了用于计算非线性赫兹接触力的公式。Serweta W[5]利用非线性赫兹接触理论，比较了两个具有冲击的系统的动力学行为，分析了其分岔特性。本文建立了一种类似于摇枕侧架系统与车身具有相互碰撞挡块的力学模型，通过对其分岔图、相图以及庞加莱截面图的研究，分析了系统的动力学特性。

2 弹跳碰撞系统模型及其运动方程

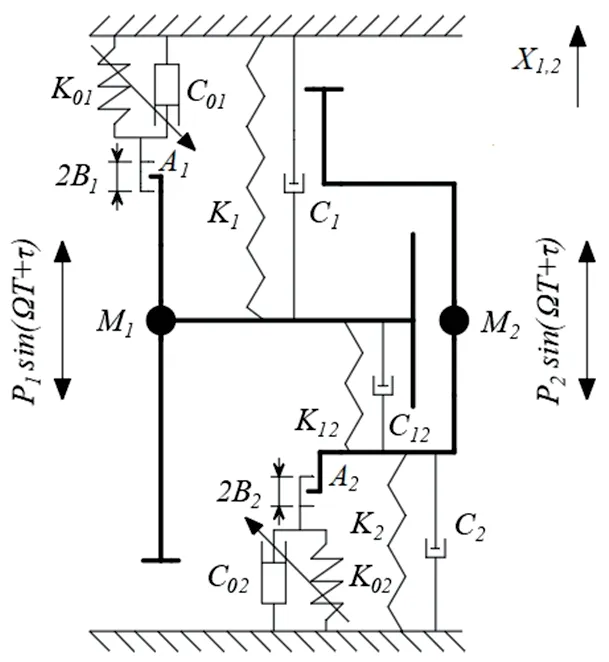
图1 两自由度赫兹接触弹跳碰撞振动系统

两个质量块仅在垂直方向上振动，若简谐激振力较小，碰撞系统表现为非冲击强迫振动。随着简谐激振力加大，质量块向止动块的位移增加到间隙阈值时，质量块将会冲击相应的止动块。文章只考虑质量块在任意两次连续碰撞间的运动过程。

根据牛顿运动定律，推导出系统运动的2自由度微分方程：

其中：

模型的赫兹接触力表示如下：

为方便研究，引入无量纲变量和参数如下：

无量纲后的运动微分方程为：

其中，非线性赫兹接触力：

系统经过无量纲化后，可以方便的确定部分参数的取值范围：

根据式子建立系统的Poincaré映射截面：

3 数值仿真

参数对系统的影响如下所示。接着继续分析了弹跳间隙以及接触刚度分配系数以及接触阻尼分配系数改变时，对弹跳碰撞系统分岔特性的影响。首先保持系统基准参数不变，增大弹跳间隙的值，各参数下的系统分岔图如图4（a）、图4（b）所示。对比图2可得出结论，即当其它参数保持不变时，随着间隙的减小，系统的动力学性能逐渐开始变得丰富，系统混沌运动的区域也变大。应在合理的范围内，使间隙取相对较大的值。再恢复基准参数，增大接触刚度分配系数的值，系统的周期分岔如图4（c）、图4（d）所示，通过对比图2，可以知道，当其它参数在给定值下保持不变时，随着接触刚度系数的增大，系统混沌运动的区域在逐渐变大，而且可以发现系统的动力学性能对此参数数值较为敏感。为了保证系统可以稳定的运动，接触刚度系数应该取较小值。之后再恢复至基础参数，保持其他参数不变，改变接触阻尼分配系数，观察如图4（e）、图4（f）所示的系统分岔图，可以知道，随着接触阻尼分配系数的增大，系统的动力学行为变得简单，基本以一周期、二周期为主，只有少量的混沌区域。为了保证系统稳定性，接触阻尼分配系数应该取相对较大的值。

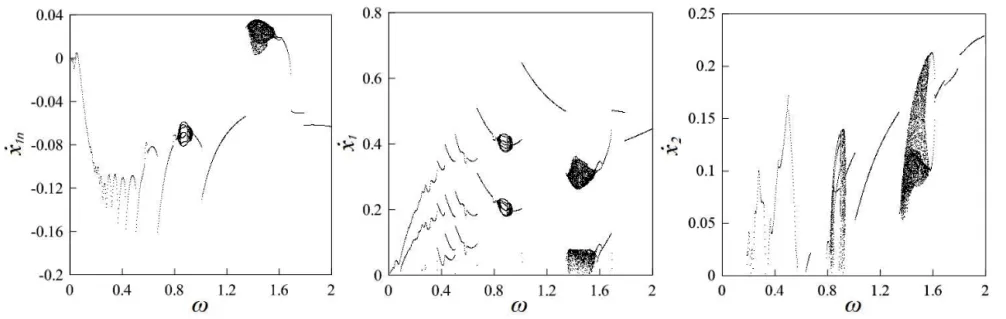
图2 系统在频率分岔图

图3 倍化分岔各阶段相图与庞加莱截面图叠加图

图4 参数变化时系统分岔图

4 结束语

本文建立研究了一种两自由度赫兹接触弹跳碰撞振动系统模型，分析了其运动特性，在选定的参数下，使用Runge-Kutta法，对方程进行了数值积分，画出了弹跳碰撞系统在振动频率区间的分岔图、相图，分析了其分岔特性，并用控制变量法，研究了系统中弹跳间隙和接触刚度分配系数以及接触阻尼分配系数对系统运动特性的影响，经过比对，发现弹跳间隙在合理范围内应取相对较大的值，接触刚度分配系数应取较小值，而接触阻尼分配系数取较大值为宜。